2025年安徽省黄山市中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年安徽省黄山市中考数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 19:17:54 | ||
图片预览


文档简介
2025年安徽省黄山市中考数学模拟试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数,在数轴上的对应点的位置如图所示,则下列关系正确的是( )
A. B. C. D.
2.根据国际能源署年全球可再生能源展望报告,预计年全球太阳能发电总装机容量将达到千瓦下列用科学记数法表示该数据正确的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.我国古代建筑中经常使用榫卯构件,如图是某种榫构件示意图,则榫的俯视图是( )
A. B.
C. D.
5.如图,数轴上公共部分表示的是某个关于的一元一次不等式组的解集,那么这个不等式组可以是( )
A. B. C. D.
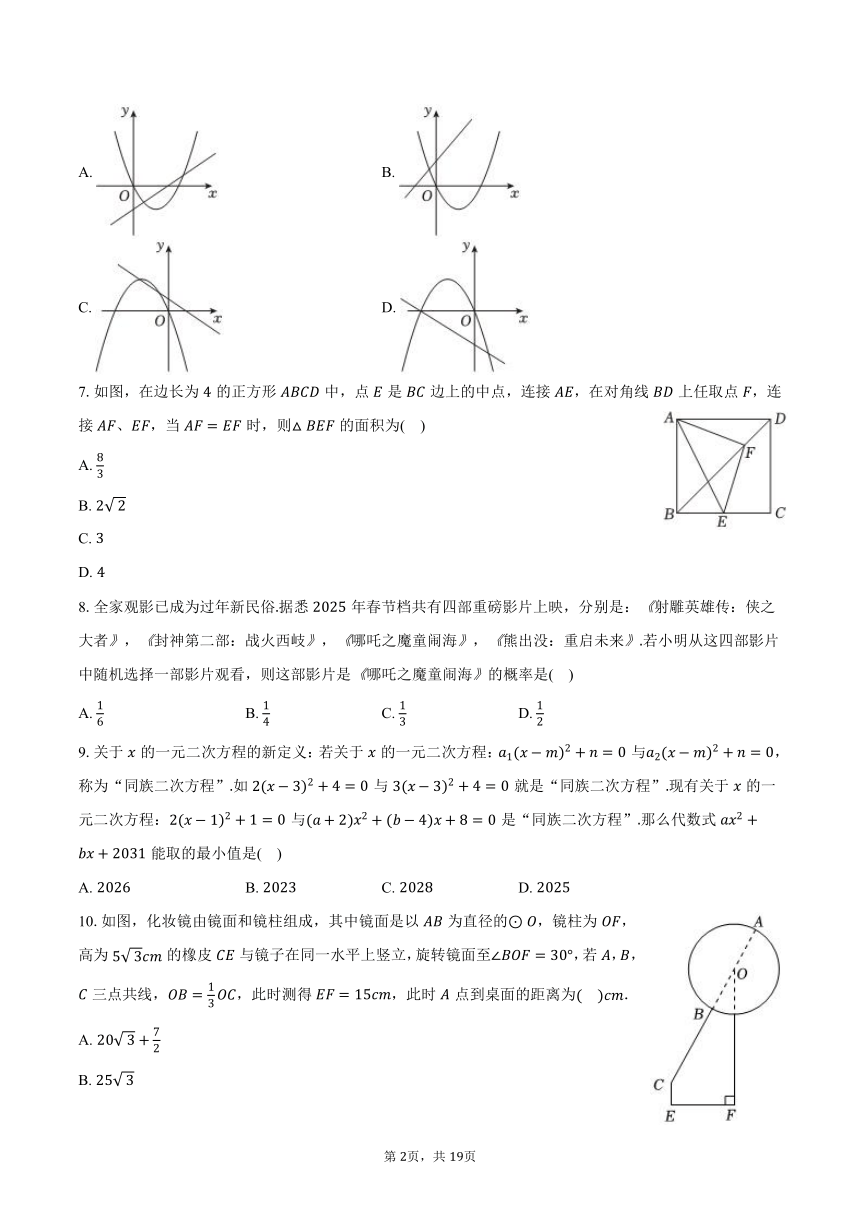
6.在同一平面直角坐标系中,一次函数为常数,且的图象与二次函数的图象可能是( )
A. B.
C. D.
7.如图,在边长为的正方形中,点是边上的中点,连接,在对角线上任取点,连接、,当时,则的面积为( )
A.
B.
C.
D.
8.全家观影已成为过年新民俗据悉年春节档共有四部重磅影片上映,分别是:射雕英雄传:侠之大者,封神第二部:战火西岐,哪吒之魔童闹海,:重启未来若小明从这四部影片中随机选择一部影片观看,则这部影片是哪吒之魔童闹海的概率是( )
A. B. C. D.
9.关于的一元二次方程的新定义:若关于的一元二次方程:与,称为“同族二次方程”如与就是“同族二次方程”现有关于的一元二次方程:与是“同族二次方程”那么代数式能取的最小值是( )
A. B. C. D.
10.如图,化妆镜由镜面和镜柱组成,其中镜面是以为直径的,镜柱为,高为的橡皮与镜子在同一水平上竖立,旋转镜面至,若,,三点共线,,此时测得,此时点到桌面的距离为.
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分。
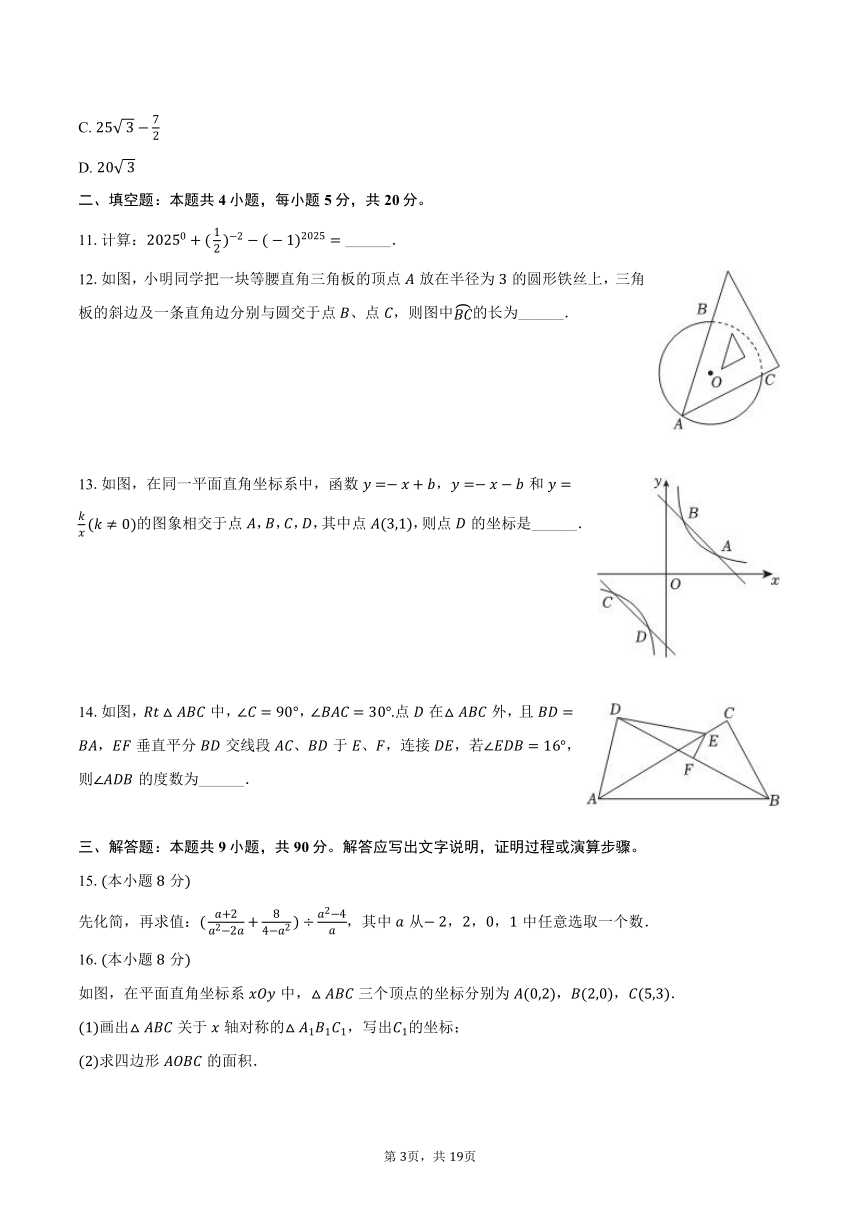
11.计算: ______.
12.如图,小明同学把一块等腰直角三角板的顶点放在半径为的圆形铁丝上,三角板的斜边及一条直角边分别与圆交于点、点,则图中的长为______.
13.如图,在同一平面直角坐标系中,函数,和的图象相交于点,,,,其中点,则点的坐标是______.
14.如图,中,,点在外,且,垂直平分交线段、于、,连接,若,则的度数为______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
先化简,再求值:,其中从,,,中任意选取一个数.
16.本小题分
如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
画出关于轴对称的,写出的坐标;
求四边形的面积.
17.本小题分
【阅读材料】对于任意实数,都有.
当分别取值,,,,,时,得到下列有一定规律的等式:
第个等式;
第个等式;
第个等式;
第个等式;
第个等式;
把以上个等式相加,并整理、化简,
得,
进一步化简,得.
【初步理解】有一列数,,,,满足以下等式:
,,,,,
根据阅读材料、以上等式所包含的规律,解决问题:
______;
______;______;用含的代数式表示
【深化应用】
结合阅读材料、等式,求的值.
18.本小题分
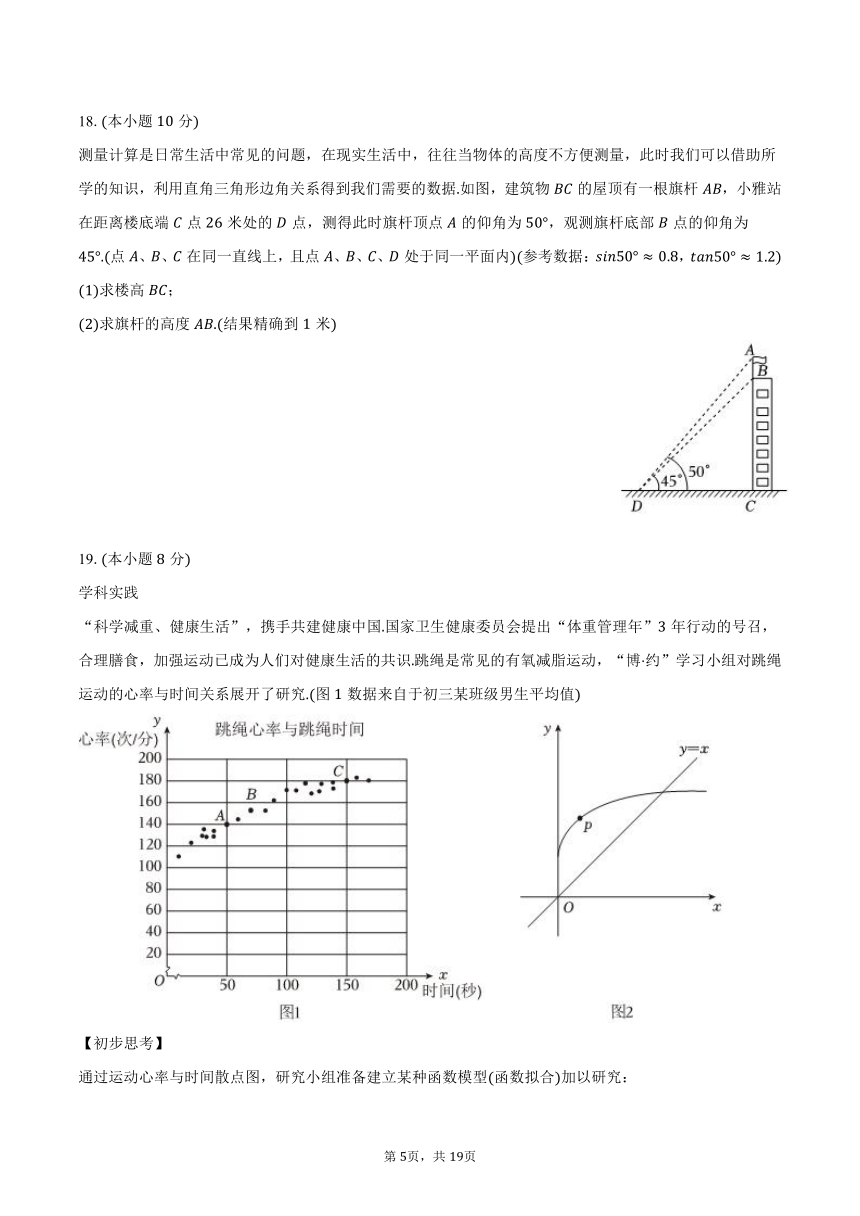
测量计算是日常生活中常见的问题,在现实生活中,往往当物体的高度不方便测量,此时我们可以借助所学的知识,利用直角三角形边角关系得到我们需要的数据如图,建筑物的屋顶有一根旗杆,小雅站在距离楼底端点米处的点,测得此时旗杆顶点的仰角为,观测旗杆底部点的仰角为点、、在同一直线上,且点、、、处于同一平面内参考数据:,
求楼高;
求旗杆的高度结果精确到米
19.本小题分
学科实践
“科学减重、健康生活”,携手共建健康中国国家卫生健康委员会提出“体重管理年”年行动的号召,合理膳食,加强运动已成为人们对健康生活的共识跳绳是常见的有氧减脂运动,“博约”学习小组对跳绳运动的心率与时间关系展开了研究图数据来自于初三某班级男生平均值
【初步思考】
通过运动心率与时间散点图,研究小组准备建立某种函数模型函数拟合加以研究:
甲:心率不会随时间的增加而不断增加,也不会明显下降,一次函数不太合理;
乙:运动一段时间后,心率应该趋于相对稳定;
丙:所以二次函数也不能很好地预测长时间运动后的心率情况;
丁:我们可以建立将反比例函数图象经过适当平移后的函数模型
设拟合函数为:
【问题解决】
如图,若选取,,进行拟合,经计算,请求出拟合函数表达式.
从健康角度考虑,中学生运动中的心率不宜超过次分钟,在的条件下,请问:跳绳运动几分钟后就应该休息一下?
根据图象变换,中图象可由的图象向左平移______个单位,再向上平移______个单位得到:
点在中图象上运动,且位于直线左侧,当点到直线距离最大时,达到最佳运动心率,请直接写出达到最佳运动心率的时间.
20.本小题分
如图,过外一点作的切线,切点为点,为的直径,点为上一点,且,连接,,线段交直径于点,交于点,连接.
求证:;
若,,求的半径长.
21.本小题分
“华罗庚数学奖”是中国三大顶尖数学奖项之一,是为激励中国数学家在发展中国数学事业中做出突出贡献而设立的小华对截止到第十六届“华罗庚数学奖”得主获奖时的年龄单位:岁数据进行了收集、整理和分析下面是部分信息.
“华罗庚数学奖”得主获奖时的年龄统计图数据分成组:,,,,:
“华罗庚数学奖”得主获奖时的年龄在这一组的是:
“华罗庚数学奖”得主获奖时的年龄数据的平均数、中位数、众数如下:
平均数 中位数 众数
,
根据以上信息,回答下列问题:
截止到第十六届共有______人获得“华罗庚数学奖”;
补全“华罗庚数学奖”得主获奖年龄频数分布直方图;
第十六届“华罗庚数学奖”得主徐宗本院士获奖时的年龄为岁,他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄______填“小”或“大”,理由是______;
22.本小题分
如图,已知二次函数的图象与轴交于,两点,与轴交于点,其中,.
求该二次函数的顶点坐标;
若是二次函数图象上的一点,且点在第一象限,的面积是面积的一半,求点的坐标.
23.本小题分
友好图形的定义如下:两个完全重合放置的图形,固定一个顶点,将其中一个图形绕这个顶点旋转,这样的图形称为友好图形,下面我们来探究友好图形旋转的性质.
已知矩形,将矩形绕点旋转到矩形,,.
【尝试发现】
如图,连接,,在旋转过程中,探究 ______;
【类比探究】
如图,在矩形绕点旋转的过程中,使落在矩形对角线上,矩形对角线与相交于点,交于,延长交于点,求的长.
【联系拓广】
将友好矩形中的绕点旋转到的过程中,当构成直角三角形时,求出的长.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:
,
当时,原式.
16.【解析】,,关于轴对称的点分别为,,,描出这三个点,再顺次连接,如图所示,即为所求,
如下图所示,.
17.【解析】有一列数,,,,满足以下等式:
,,,,,
,
故答案为:;
由归纳可得:;
,,,,,,
把所有的等式相加可得:
;
故答案为:;;
,
,
,
,
,
,
,
整理得:,
,
18.【解析】由题意得:,
在中,,米,
米,
楼高为米;
在中,,米,
米,
米,
旗杆的高度约为米.
19.【解析】由条件可得:
.
用第二个方程减去第一个方程消去:
,
,
,
,
解得或舍去,因为 .
把代入,可得,,
解得.
拟合函数表达式为.
令,可得.
解得,
分钟.
跳绳运动分钟后就应该休息一下;
函数到,根据“左加右减,上加下减”原则,变为,图象向左平移了个单位;整体加,图象向上平移了个单位.
故答案为:,;
设与直线平行的直线方程为.
该直线与曲线相切时,该切点到的距离最大,
联立方程,
得到.
.
,
.
直线与曲线相切,
联立后的一元二次方程的判别式.
.
.
的解为,
舍去或,
最佳运动心率的时间为秒.
20.【解析】证明:为的切线,
,
,
为的直径,
,
,
,
,
,
又,
,
;
为的切线,,,如图,连接.
,
,,
,
,
,
,
设,则,
在中,,,
,
为直径,
,
,,
,
,
在中,,
.
,
,
解得,
,
半径的长为.
21.【解析】人,
即截止到第十六届共有人获得“华罗庚数学奖”,
故答案为:;
年龄段的得主获奖人数为:人,
补全频数分布直方图如下:
获奖年龄的中位数为第和名年龄的平均数,
年龄段有人,年龄段有人,
第和名年龄在年龄段,分别为岁和岁,
“华罗庚数学奖”得主获奖年龄的中位数岁,
徐宗本院士获奖时的年龄为岁,
他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄小,理由是徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
故答案为:小,徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
22.【解析】由题意可得:
,
解得,
,
该二次函数的顶点坐标为;
当时,,
解得,,
,
,
.
设直线的解析式为,
将,代入得:
,
解得,
直线的解析式为,
作轴交于,
设,
则,
,
,
,
整理得,
解得,,
当时,,
当时,.
23.【解析】将矩形绕点旋转到矩形,
,,
,
,,
,
∽,
,
故答案为:;
如图,连接,
根据旋转可得,,
,
四边形是矩形,
,,
,
,
,
∽,
,
,
,
,,
,
,
∽,
,即,
解得,经检验是原方程的解,
;
如图,点在上时,,
,,
,
;
如图,点在延长线上时,,
此时,
;
如图,当时,过点作于点,
四边形为矩形,
,,
根据勾股定理可得,
;
如图,当时,过点作交,于点,,
,,
,
,,
∽,
,
,,
在中,,
,,
∽,
,
,
,
,
,
综上所述,的长为或或或.
第16页,共19页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数,在数轴上的对应点的位置如图所示,则下列关系正确的是( )
A. B. C. D.
2.根据国际能源署年全球可再生能源展望报告,预计年全球太阳能发电总装机容量将达到千瓦下列用科学记数法表示该数据正确的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B.
C. D.
4.我国古代建筑中经常使用榫卯构件,如图是某种榫构件示意图,则榫的俯视图是( )
A. B.
C. D.
5.如图,数轴上公共部分表示的是某个关于的一元一次不等式组的解集,那么这个不等式组可以是( )
A. B. C. D.
6.在同一平面直角坐标系中,一次函数为常数,且的图象与二次函数的图象可能是( )
A. B.
C. D.
7.如图,在边长为的正方形中,点是边上的中点,连接,在对角线上任取点,连接、,当时,则的面积为( )
A.
B.
C.
D.
8.全家观影已成为过年新民俗据悉年春节档共有四部重磅影片上映,分别是:射雕英雄传:侠之大者,封神第二部:战火西岐,哪吒之魔童闹海,:重启未来若小明从这四部影片中随机选择一部影片观看,则这部影片是哪吒之魔童闹海的概率是( )
A. B. C. D.
9.关于的一元二次方程的新定义:若关于的一元二次方程:与,称为“同族二次方程”如与就是“同族二次方程”现有关于的一元二次方程:与是“同族二次方程”那么代数式能取的最小值是( )
A. B. C. D.
10.如图,化妆镜由镜面和镜柱组成,其中镜面是以为直径的,镜柱为,高为的橡皮与镜子在同一水平上竖立,旋转镜面至,若,,三点共线,,此时测得,此时点到桌面的距离为.
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分。
11.计算: ______.
12.如图,小明同学把一块等腰直角三角板的顶点放在半径为的圆形铁丝上,三角板的斜边及一条直角边分别与圆交于点、点,则图中的长为______.
13.如图,在同一平面直角坐标系中,函数,和的图象相交于点,,,,其中点,则点的坐标是______.
14.如图,中,,点在外,且,垂直平分交线段、于、,连接,若,则的度数为______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
先化简,再求值:,其中从,,,中任意选取一个数.
16.本小题分
如图,在平面直角坐标系中,三个顶点的坐标分别为,,.
画出关于轴对称的,写出的坐标;
求四边形的面积.
17.本小题分
【阅读材料】对于任意实数,都有.
当分别取值,,,,,时,得到下列有一定规律的等式:
第个等式;
第个等式;
第个等式;
第个等式;
第个等式;
把以上个等式相加,并整理、化简,
得,
进一步化简,得.
【初步理解】有一列数,,,,满足以下等式:
,,,,,
根据阅读材料、以上等式所包含的规律,解决问题:
______;
______;______;用含的代数式表示
【深化应用】
结合阅读材料、等式,求的值.
18.本小题分
测量计算是日常生活中常见的问题,在现实生活中,往往当物体的高度不方便测量,此时我们可以借助所学的知识,利用直角三角形边角关系得到我们需要的数据如图,建筑物的屋顶有一根旗杆,小雅站在距离楼底端点米处的点,测得此时旗杆顶点的仰角为,观测旗杆底部点的仰角为点、、在同一直线上,且点、、、处于同一平面内参考数据:,
求楼高;
求旗杆的高度结果精确到米
19.本小题分
学科实践
“科学减重、健康生活”,携手共建健康中国国家卫生健康委员会提出“体重管理年”年行动的号召,合理膳食,加强运动已成为人们对健康生活的共识跳绳是常见的有氧减脂运动,“博约”学习小组对跳绳运动的心率与时间关系展开了研究图数据来自于初三某班级男生平均值
【初步思考】
通过运动心率与时间散点图,研究小组准备建立某种函数模型函数拟合加以研究:
甲:心率不会随时间的增加而不断增加,也不会明显下降,一次函数不太合理;
乙:运动一段时间后,心率应该趋于相对稳定;
丙:所以二次函数也不能很好地预测长时间运动后的心率情况;
丁:我们可以建立将反比例函数图象经过适当平移后的函数模型
设拟合函数为:
【问题解决】
如图,若选取,,进行拟合,经计算,请求出拟合函数表达式.
从健康角度考虑,中学生运动中的心率不宜超过次分钟,在的条件下,请问:跳绳运动几分钟后就应该休息一下?
根据图象变换,中图象可由的图象向左平移______个单位,再向上平移______个单位得到:
点在中图象上运动,且位于直线左侧,当点到直线距离最大时,达到最佳运动心率,请直接写出达到最佳运动心率的时间.
20.本小题分
如图,过外一点作的切线,切点为点,为的直径,点为上一点,且,连接,,线段交直径于点,交于点,连接.
求证:;
若,,求的半径长.
21.本小题分
“华罗庚数学奖”是中国三大顶尖数学奖项之一,是为激励中国数学家在发展中国数学事业中做出突出贡献而设立的小华对截止到第十六届“华罗庚数学奖”得主获奖时的年龄单位:岁数据进行了收集、整理和分析下面是部分信息.
“华罗庚数学奖”得主获奖时的年龄统计图数据分成组:,,,,:
“华罗庚数学奖”得主获奖时的年龄在这一组的是:
“华罗庚数学奖”得主获奖时的年龄数据的平均数、中位数、众数如下:
平均数 中位数 众数
,
根据以上信息,回答下列问题:
截止到第十六届共有______人获得“华罗庚数学奖”;
补全“华罗庚数学奖”得主获奖年龄频数分布直方图;
第十六届“华罗庚数学奖”得主徐宗本院士获奖时的年龄为岁,他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄______填“小”或“大”,理由是______;
22.本小题分
如图,已知二次函数的图象与轴交于,两点,与轴交于点,其中,.
求该二次函数的顶点坐标;
若是二次函数图象上的一点,且点在第一象限,的面积是面积的一半,求点的坐标.
23.本小题分
友好图形的定义如下:两个完全重合放置的图形,固定一个顶点,将其中一个图形绕这个顶点旋转,这样的图形称为友好图形,下面我们来探究友好图形旋转的性质.
已知矩形,将矩形绕点旋转到矩形,,.
【尝试发现】
如图,连接,,在旋转过程中,探究 ______;
【类比探究】
如图,在矩形绕点旋转的过程中,使落在矩形对角线上,矩形对角线与相交于点,交于,延长交于点,求的长.
【联系拓广】
将友好矩形中的绕点旋转到的过程中,当构成直角三角形时,求出的长.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:
,
当时,原式.
16.【解析】,,关于轴对称的点分别为,,,描出这三个点,再顺次连接,如图所示,即为所求,
如下图所示,.
17.【解析】有一列数,,,,满足以下等式:
,,,,,
,
故答案为:;
由归纳可得:;
,,,,,,
把所有的等式相加可得:
;
故答案为:;;
,
,
,
,
,
,
,
整理得:,
,
18.【解析】由题意得:,
在中,,米,
米,
楼高为米;
在中,,米,
米,
米,
旗杆的高度约为米.
19.【解析】由条件可得:
.
用第二个方程减去第一个方程消去:
,
,
,
,
解得或舍去,因为 .
把代入,可得,,
解得.
拟合函数表达式为.
令,可得.
解得,
分钟.
跳绳运动分钟后就应该休息一下;
函数到,根据“左加右减,上加下减”原则,变为,图象向左平移了个单位;整体加,图象向上平移了个单位.
故答案为:,;
设与直线平行的直线方程为.
该直线与曲线相切时,该切点到的距离最大,
联立方程,
得到.
.
,
.
直线与曲线相切,
联立后的一元二次方程的判别式.
.
.
的解为,
舍去或,
最佳运动心率的时间为秒.
20.【解析】证明:为的切线,
,
,
为的直径,
,
,
,
,
,
又,
,
;
为的切线,,,如图,连接.
,
,,
,
,
,
,
设,则,
在中,,,
,
为直径,
,
,,
,
,
在中,,
.
,
,
解得,
,
半径的长为.
21.【解析】人,
即截止到第十六届共有人获得“华罗庚数学奖”,
故答案为:;
年龄段的得主获奖人数为:人,
补全频数分布直方图如下:
获奖年龄的中位数为第和名年龄的平均数,
年龄段有人,年龄段有人,
第和名年龄在年龄段,分别为岁和岁,
“华罗庚数学奖”得主获奖年龄的中位数岁,
徐宗本院士获奖时的年龄为岁,
他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄小,理由是徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
故答案为:小,徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
22.【解析】由题意可得:
,
解得,
,
该二次函数的顶点坐标为;
当时,,
解得,,
,
,
.
设直线的解析式为,
将,代入得:
,
解得,
直线的解析式为,
作轴交于,
设,
则,
,
,
,
整理得,
解得,,
当时,,
当时,.
23.【解析】将矩形绕点旋转到矩形,
,,
,
,,
,
∽,
,
故答案为:;
如图,连接,
根据旋转可得,,
,
四边形是矩形,
,,
,
,
,
∽,
,
,
,
,,
,
,
∽,
,即,
解得,经检验是原方程的解,
;
如图,点在上时,,
,,
,
;
如图,点在延长线上时,,
此时,
;
如图,当时,过点作于点,
四边形为矩形,
,,
根据勾股定理可得,
;
如图,当时,过点作交,于点,,
,,
,
,,
∽,
,
,,
在中,,
,,
∽,
,
,
,
,
,
综上所述,的长为或或或.
第16页,共19页
同课章节目录
