2.2.4均值不等式及其应用(教学课件)——高中数学人教B版(2019)必修第一册(共33张PPT)
文档属性
| 名称 | 2.2.4均值不等式及其应用(教学课件)——高中数学人教B版(2019)必修第一册(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 42.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 19:23:04 | ||
图片预览










文档简介
(共33张PPT)
2.2.4均值不等式及其应用
人教B版(2019)必修第一册
第二章 等式与不等式
学习目标
掌握均值不等式
01
掌握两个正变量的和或积为常数的最值问题
02
掌握均值不等式的实际应用
03
探索新知
给定两个正数 a,b,数 称为 a,b 的算术平均值;
数 称为 a,b 的几何平均值.
两个数的算术平均值,实质上是这两个数在数轴上对应的点的中点坐标,那么几何平均值有什么几何意义呢?两个数的算术平均值和几何平均值之间有什么相对大小关系呢?
探索新知
尝试与发现
(1) 假设一个矩形的长和宽分别为 a 和 b,求与这个矩形周长相等的正方形的边长,以及与这个矩形面积相等的正方形的边长,并比较这两个边长的大小;
探索新知
尝试与发现
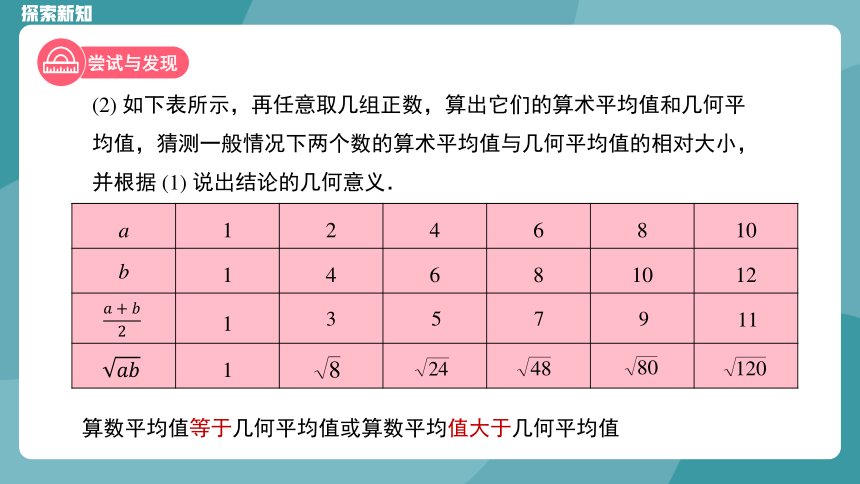
(2) 如下表所示,再任意取几组正数,算出它们的算术平均值和几何平均值,猜测一般情况下两个数的算术平均值与几何平均值的相对大小,并根据 (1) 说出结论的几何意义.
a 1 2 4 6 8 10
b 1 4 6 8 10 12
1
1
算数平均值等于几何平均值或算数平均值大于几何平均值
探索新知
均值不等式
如果 a,b 都是正数,那么 ,
当且仅当 a=b 时,等号成立.
证明 因为 a,b 都是正数,所以
即
而且,等号成立时,当且仅当 ,即 a=b.
探索新知
思考:能否通过重要不等式证明均值不等式?
方法一
方法二
且
用分别代替
有:
即:
探索新知
值得注意的是,均值不等式中的 a,b 可以是任意正实数,因此我们可以代入任意满足条件的数或式子,比如 一定是正确的.
均值不等式也称为基本不等式(基本不等式中的 a,b 还可以为零),其实质是:两个正实数的算术平均值不小于它们的几何平均值.那么,均值不等式有什么几何意义呢?
探索新知
均值不等式的几何意义
将均值不等式两边平方可得 ≥ab.
如果矩形的长和宽分别为a和b,那么矩形的面积为ab, 可以看成与矩形周长相等的正方形的面积,因此均值不等式的一个几何意义为:所有周长一定的矩形中,正方形的面积最大.
探索新知
想一想
你能推广这个结论吗?比如所有周长相等的三角形中,什么样的三角形面积最大?平面上,周长相等的所有封闭图形中,什么样的图形面积最大?
周长相等的三角形中,正三角形的面积最大. 平面上,周长相等的所有封闭图形中,圆的面积最大,当周长一定时,正多边形的面积随着边数的增加而增加,当边数趋近于正无穷时,边长趋近于一个点,正多边形的形状趋近圆,故圆的面积最大.
探索新知
探索与研究
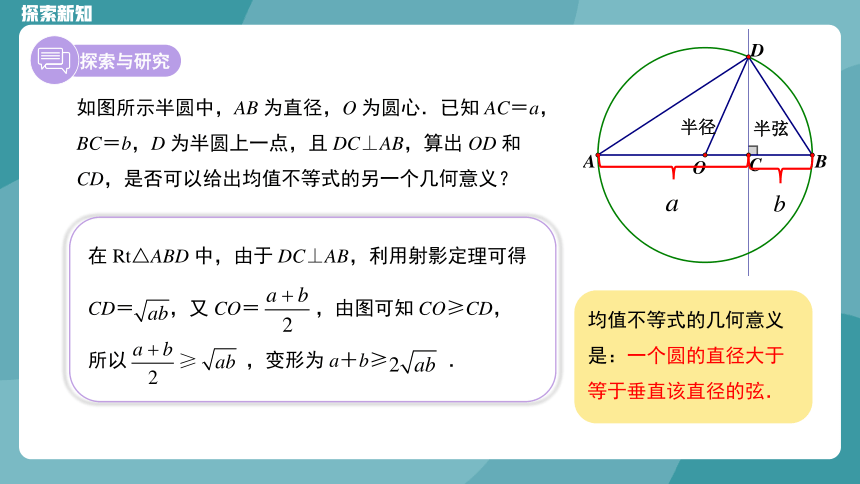
如图所示半圆中,AB 为直径,O 为圆心.已知 AC=a,BC=b,D 为半圆上一点,且 DC⊥AB,算出 OD 和 CD,是否可以给出均值不等式的另一个几何意义?
半径
半弦
在 Rt△ABD 中,由于 DC⊥AB,利用射影定理可得
CD= ,又 CO= ,由图可知 CO≥CD,
所以 ,变形为 a+b≥ .
均值不等式的几何意义是:一个圆的直径大于等于垂直该直径的弦.
探索新知
一元二次不等式的解集
一般地,如果 x1<x2,则不等式 (x-x1)(x-x2)<0 的解集是(x1,x2),
不等式 (x-x1)(x-x2)>0 的解集是
(-∞,x1)∪(x2,+∞).
典型例题
例 1 已知 x>0,求 y=x+ 的最小值,并说明 x 为何值时 y取得最小值.
典型例题
例 2 已知 ,求证 , 并推导出等号成立的条件.
典型例题
例 3 (1) 已知矩形的面积为 100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
分析:在 (1) 中,矩形的长与宽的积是一个常数,要求长与宽之和的两倍的最小值;
解:(1) 设矩形的长与宽分别为 x 与 y,依题意得 xy=100.
所以 2 (x+y)≥40.
因为 x>0,y>0,所以 ,
因此,当矩形的长和宽都是 10 时,它的周长最短,最短周长为 40.
当且仅当 x=y 时,等号成立,
由 ,可知此时 x=y=10.
典型例题
例 3 (2) 已知矩形的周长为 36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
分析:在 (2) 中,矩形的长与宽之和的两倍是一个常数,要求长与宽的积的最大值.
解: (2) 设矩形的长与宽分别为 x 与 y,
依题意得 2 (x+y) =36,即 x+y=18.
因为 x>0,y>0,所以 ,
因此 ≤9,即 xy≤81.
当且仅当 x=y 时,等号成立,由 ,可知此时 x=y=9.
因此,当矩形的长和宽都是 9 时,它的面积最大,最大面积为 81.
当两个正数的积为常数时,它们的和有最小值;
当两个正数的和为常数时,它们的积有最大值.
例 4
典型例题
例 5 已知 a,b 是实数,求证:a2+b2≥2ab.并说明等号成立的条件
典型例题
证明:因为 a2+b2-2ab=(a-b)2≥0,
所以 a2+b2-2ab≥0,即 a2+b2≥2ab.
等号成立时,当且仅当 (a-b)2=0,即 a=b.
例 5 的结论也是经常要用的. 不难看出,均值不等式与例 5 的结论既有联系,又有区别. 区别在于例 5 中去掉了 a,b 是正数的条件,联系在于均值不等式可以看成例 5 结论的一种特殊情况.
例 6 已知a,b∈R,求证:
(1) (a+b) 2≥4ab;
(2) 2(a2+b2) ≥(a+b) 2.
典型例题
证明: (1) 因为 a2+b2≥2ab,两边同时加上 2ab,得
a2+b2+2ab≥4ab,
即 (a+b)2≥4ab;
例 6 已知a,b∈R,求证:
(1) (a+b) 2≥4ab;
(2) 2(a2+b2) ≥(a+b) 2.
典型例题
证明: (2) 因为 a2+b2≥2ab,两边同时加上 a2+b2,得
2(a2+b2) ≥a2+b2+2ab,
即 2(a2+b2) ≥(a+b) 2.
(a+b) 2≥4ab 以及 2(a2+b2)≥(a+b) 2 都是均值不等式的变形,
又其中 2(a2+b2)≥(a+b) 2 又常变形为 .
探索新知
探索与研究
用 Excel 或其他计算机软件,完成下列数学实验:
(1) 任取多组三个正数 a,b,c,计算 和 运后,比较它们的大小,总结出一般规律;
(2) 对四个正数、五个正数做同样的实验,总结出普遍规律.
一般地, ,
当且仅当 a1=a2=…=an 时,等号成立.
当堂检测
当堂检测
B
当堂检测
D
当堂检测
C
当堂检测
当堂检测
当堂检测
C
当堂检测
当堂检测
当堂检测
本节课学习了哪些知识点呢?
1.均值不等式;
2.均值不等式的变式与推广.
感谢观看
祝同学新学期新气象
2.2.4均值不等式及其应用
人教B版(2019)必修第一册
第二章 等式与不等式
学习目标
掌握均值不等式
01
掌握两个正变量的和或积为常数的最值问题
02
掌握均值不等式的实际应用
03
探索新知
给定两个正数 a,b,数 称为 a,b 的算术平均值;
数 称为 a,b 的几何平均值.
两个数的算术平均值,实质上是这两个数在数轴上对应的点的中点坐标,那么几何平均值有什么几何意义呢?两个数的算术平均值和几何平均值之间有什么相对大小关系呢?
探索新知
尝试与发现
(1) 假设一个矩形的长和宽分别为 a 和 b,求与这个矩形周长相等的正方形的边长,以及与这个矩形面积相等的正方形的边长,并比较这两个边长的大小;
探索新知
尝试与发现
(2) 如下表所示,再任意取几组正数,算出它们的算术平均值和几何平均值,猜测一般情况下两个数的算术平均值与几何平均值的相对大小,并根据 (1) 说出结论的几何意义.
a 1 2 4 6 8 10
b 1 4 6 8 10 12
1
1
算数平均值等于几何平均值或算数平均值大于几何平均值
探索新知
均值不等式
如果 a,b 都是正数,那么 ,
当且仅当 a=b 时,等号成立.
证明 因为 a,b 都是正数,所以
即
而且,等号成立时,当且仅当 ,即 a=b.
探索新知
思考:能否通过重要不等式证明均值不等式?
方法一
方法二
且
用分别代替
有:
即:
探索新知
值得注意的是,均值不等式中的 a,b 可以是任意正实数,因此我们可以代入任意满足条件的数或式子,比如 一定是正确的.
均值不等式也称为基本不等式(基本不等式中的 a,b 还可以为零),其实质是:两个正实数的算术平均值不小于它们的几何平均值.那么,均值不等式有什么几何意义呢?
探索新知
均值不等式的几何意义
将均值不等式两边平方可得 ≥ab.
如果矩形的长和宽分别为a和b,那么矩形的面积为ab, 可以看成与矩形周长相等的正方形的面积,因此均值不等式的一个几何意义为:所有周长一定的矩形中,正方形的面积最大.
探索新知
想一想
你能推广这个结论吗?比如所有周长相等的三角形中,什么样的三角形面积最大?平面上,周长相等的所有封闭图形中,什么样的图形面积最大?
周长相等的三角形中,正三角形的面积最大. 平面上,周长相等的所有封闭图形中,圆的面积最大,当周长一定时,正多边形的面积随着边数的增加而增加,当边数趋近于正无穷时,边长趋近于一个点,正多边形的形状趋近圆,故圆的面积最大.
探索新知
探索与研究
如图所示半圆中,AB 为直径,O 为圆心.已知 AC=a,BC=b,D 为半圆上一点,且 DC⊥AB,算出 OD 和 CD,是否可以给出均值不等式的另一个几何意义?
半径
半弦
在 Rt△ABD 中,由于 DC⊥AB,利用射影定理可得
CD= ,又 CO= ,由图可知 CO≥CD,
所以 ,变形为 a+b≥ .
均值不等式的几何意义是:一个圆的直径大于等于垂直该直径的弦.
探索新知
一元二次不等式的解集
一般地,如果 x1<x2,则不等式 (x-x1)(x-x2)<0 的解集是(x1,x2),
不等式 (x-x1)(x-x2)>0 的解集是
(-∞,x1)∪(x2,+∞).
典型例题
例 1 已知 x>0,求 y=x+ 的最小值,并说明 x 为何值时 y取得最小值.
典型例题
例 2 已知 ,求证 , 并推导出等号成立的条件.
典型例题
例 3 (1) 已知矩形的面积为 100,则这个矩形的长、宽各为多少时,矩形的周长最短?最短周长是多少?
分析:在 (1) 中,矩形的长与宽的积是一个常数,要求长与宽之和的两倍的最小值;
解:(1) 设矩形的长与宽分别为 x 与 y,依题意得 xy=100.
所以 2 (x+y)≥40.
因为 x>0,y>0,所以 ,
因此,当矩形的长和宽都是 10 时,它的周长最短,最短周长为 40.
当且仅当 x=y 时,等号成立,
由 ,可知此时 x=y=10.
典型例题
例 3 (2) 已知矩形的周长为 36,则这个矩形的长、宽各为多少时,它的面积最大?最大面积是多少?
分析:在 (2) 中,矩形的长与宽之和的两倍是一个常数,要求长与宽的积的最大值.
解: (2) 设矩形的长与宽分别为 x 与 y,
依题意得 2 (x+y) =36,即 x+y=18.
因为 x>0,y>0,所以 ,
因此 ≤9,即 xy≤81.
当且仅当 x=y 时,等号成立,由 ,可知此时 x=y=9.
因此,当矩形的长和宽都是 9 时,它的面积最大,最大面积为 81.
当两个正数的积为常数时,它们的和有最小值;
当两个正数的和为常数时,它们的积有最大值.
例 4
典型例题
例 5 已知 a,b 是实数,求证:a2+b2≥2ab.并说明等号成立的条件
典型例题
证明:因为 a2+b2-2ab=(a-b)2≥0,
所以 a2+b2-2ab≥0,即 a2+b2≥2ab.
等号成立时,当且仅当 (a-b)2=0,即 a=b.
例 5 的结论也是经常要用的. 不难看出,均值不等式与例 5 的结论既有联系,又有区别. 区别在于例 5 中去掉了 a,b 是正数的条件,联系在于均值不等式可以看成例 5 结论的一种特殊情况.
例 6 已知a,b∈R,求证:
(1) (a+b) 2≥4ab;
(2) 2(a2+b2) ≥(a+b) 2.
典型例题
证明: (1) 因为 a2+b2≥2ab,两边同时加上 2ab,得
a2+b2+2ab≥4ab,
即 (a+b)2≥4ab;
例 6 已知a,b∈R,求证:
(1) (a+b) 2≥4ab;
(2) 2(a2+b2) ≥(a+b) 2.
典型例题
证明: (2) 因为 a2+b2≥2ab,两边同时加上 a2+b2,得
2(a2+b2) ≥a2+b2+2ab,
即 2(a2+b2) ≥(a+b) 2.
(a+b) 2≥4ab 以及 2(a2+b2)≥(a+b) 2 都是均值不等式的变形,
又其中 2(a2+b2)≥(a+b) 2 又常变形为 .
探索新知
探索与研究
用 Excel 或其他计算机软件,完成下列数学实验:
(1) 任取多组三个正数 a,b,c,计算 和 运后,比较它们的大小,总结出一般规律;
(2) 对四个正数、五个正数做同样的实验,总结出普遍规律.
一般地, ,
当且仅当 a1=a2=…=an 时,等号成立.
当堂检测
当堂检测
B
当堂检测
D
当堂检测
C
当堂检测
当堂检测
当堂检测
C
当堂检测
当堂检测
当堂检测
本节课学习了哪些知识点呢?
1.均值不等式;
2.均值不等式的变式与推广.
感谢观看
祝同学新学期新气象
