2.1.2一元二次方程的解集及其根与系数的关系(教学课件)——高中数学人教B版(2019)必修第一册(共27张PPT)
文档属性
| 名称 | 2.1.2一元二次方程的解集及其根与系数的关系(教学课件)——高中数学人教B版(2019)必修第一册(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 58.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 19:32:14 | ||
图片预览







文档简介
(共27张PPT)
2.1.2一元二次方程的解集及其
根与系数的关系
人教B版(2019)必修第一册
第二章 等式与不等式
学习目标
理解一元二次方程的相关概念
01
掌握一元二次方程的根的判断方法,会解一元二次方程,会用韦达定理求两根的关系式的值
02
探索新知
尝试与发现
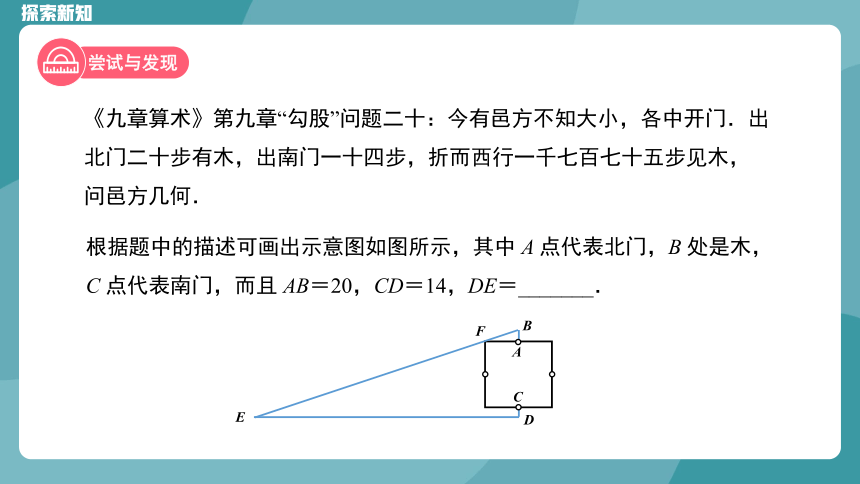
《九章算术》第九章“勾股”问题二十:今有邑方不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何.
根据题中的描述可画出示意图如图所示,其中 A 点代表北门,B 处是木,C 点代表南门,而且 AB=20,CD=14,DE=_______.
A
B
C
D
E
F
探索新知
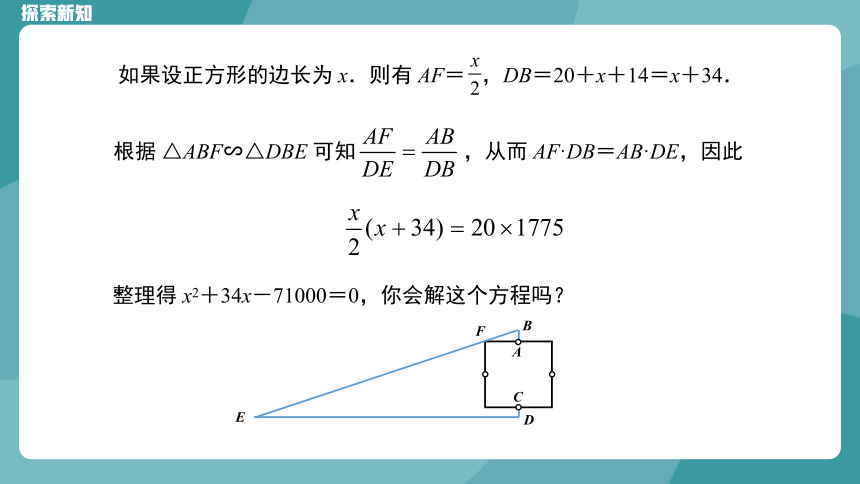
如果设正方形的边长为 x.则有 AF= ,DB=20+x+14=x+34.
根据 △ABF∽△DBE 可知 ,从而 AF·DB=AB·DE,因此
整理得 x2+34x-71000=0,你会解这个方程吗?
A
B
C
D
E
F
探索新知
我们知道,形如 ax2+bx+c=0 的方程为一元二次方程,其中 a,b,c 是常数,且 a≠0.
从上一节的内容可知,用因式分解法能得到一元二次方程的解集,但是用这种方法有时候并不容易,例如情境与问题中所得到的方程就是这种情形,此时该怎么办呢?
探索新知
尝试与发现
你认为最简单的一元二次方程具有什么样的形式?可以怎样得到这种方程的解集?举例说明.
不难知道,如果一个一元二次方程可以化为 x2=t 的形式,其中 t 为常数,那么这个方程的解集是容易获得的.
例如,方程 x2=3 的解集为{,},方程 x2=0 的解集为{0},方程 x2=2 的解集为 .
探索新知
一元二次方程的解集
一般地,方程 x2=t :
(1)当 t>0 时,解集为 ;
(2)当 t=0 时,解集为 ;
(3)当 t<0 时,解集为 .
{}
{0}
探索新知
更进一步,形如 (xk)2=t (其中 k,t 是常数) 的一元二次方程的解集也容易得到.
例如,由 (x1)2=2 可知 x1= 或 x1=,从而 x=1或 x=1,因此解集为 {1,1}.
探索新知
一元二次方程的解集
一般地,方程 (xk)2=t:
(1)当 t>0 时,解集为 ;
(2)当 t=0 时,解集为 ;
(3)当 t<0 时,解集为 .
{k,k+}
{k}
因此,对于一般的一元二次方程来说,只需要将其化为 (xk)2=t 的形式,就可得到方程的解集.
探索新知
尝试与发现
怎样将 x2+2x+3=0 化为 (x-k)2=t 的形式?动手试试看,并写出这个方程的解集.
我们知道,利用配方法可得
x2 + 2x + 3= x2 + 2x + 1+2 = (x + 1)2 + 2,
因此,x2+ 2x + 3=0 可以化为 (x +1)2 = -2,从而可知解集为 .
探索新知
事实上,利用配方法,总是可以将 ax2+bx+c=0 (a≠0) 化为 (x-k)2=t 的形式,过程如下:因为a≠0,所以
因此, ax2+bx+c=0 (a≠0) 可以化为
.
探索新知
一元二次方程的解集
从而可知,Δ=b2-4ac 的符号情况决定了上述方程的解集情况:
(1)当Δ=b2-4ac>0 时,方程的解集为
(2)当Δ=b2-4ac=0 时,方程的解集为
(3)当Δ=b2-4ac<0 时,方程的解集为 .
一般地,Δ=b2-4ac 称为一元二次方程 ax2+ bx+ c= 0 (a≠0)的判别式. 由此可知,一元二次方程解集的情况完全由它的系数决定.
例 1 求方程 的解集
典型例题
分析 这不是一个一元二次方程,但是通过把 看成一个整体就可以转化为一个一元二次方程.
解:设,则≥0,且原方程可变为 ,
因此可知 或 (舍).
从而 ,即 ,
所以原方程的解集为 .
探索新知
一元二次方程根与系数的关系
我们知道,一元二次方程 ax2+bx+c=0 (a≠0) 的解集不是空集时,这个方程的解可以记为
计算 x1+x2 和 x1x2 的值,并填空:
例 2 已知一元二次方程 2x2+3x-4=0 的两根为 x1 与 x2,求下列各式的值:
(1) x12+x22; (2) |x1-x2|.
典型例题
解:由一元二次方程根与系数的关系,得 x1+x2= ,x1x2=-2,
(1) 由上有 x12+x22=(x1+x2)2-2x1x2
=( )2-2×(-2)
(2) 因为(x1-x2)2=(x1+x2)2-4x1x2
=( )2-4×(-2)
所以 |x1-x2|= .
当堂检测
当堂检测
B
当堂检测
C
当堂检测
B
当堂检测
当堂检测
当堂检测
-1
-1
当堂检测
当堂检测
当堂检测
本节课学习了哪些知识点呢?
1.一元二次方程的解集;
2.一元二次方程根与系数的关系.
感谢观看
祝同学新学期新气象
2.1.2一元二次方程的解集及其
根与系数的关系
人教B版(2019)必修第一册
第二章 等式与不等式
学习目标
理解一元二次方程的相关概念
01
掌握一元二次方程的根的判断方法,会解一元二次方程,会用韦达定理求两根的关系式的值
02
探索新知
尝试与发现
《九章算术》第九章“勾股”问题二十:今有邑方不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何.
根据题中的描述可画出示意图如图所示,其中 A 点代表北门,B 处是木,C 点代表南门,而且 AB=20,CD=14,DE=_______.
A
B
C
D
E
F
探索新知
如果设正方形的边长为 x.则有 AF= ,DB=20+x+14=x+34.
根据 △ABF∽△DBE 可知 ,从而 AF·DB=AB·DE,因此
整理得 x2+34x-71000=0,你会解这个方程吗?
A
B
C
D
E
F
探索新知
我们知道,形如 ax2+bx+c=0 的方程为一元二次方程,其中 a,b,c 是常数,且 a≠0.
从上一节的内容可知,用因式分解法能得到一元二次方程的解集,但是用这种方法有时候并不容易,例如情境与问题中所得到的方程就是这种情形,此时该怎么办呢?
探索新知
尝试与发现
你认为最简单的一元二次方程具有什么样的形式?可以怎样得到这种方程的解集?举例说明.
不难知道,如果一个一元二次方程可以化为 x2=t 的形式,其中 t 为常数,那么这个方程的解集是容易获得的.
例如,方程 x2=3 的解集为{,},方程 x2=0 的解集为{0},方程 x2=2 的解集为 .
探索新知
一元二次方程的解集
一般地,方程 x2=t :
(1)当 t>0 时,解集为 ;
(2)当 t=0 时,解集为 ;
(3)当 t<0 时,解集为 .
{}
{0}
探索新知
更进一步,形如 (xk)2=t (其中 k,t 是常数) 的一元二次方程的解集也容易得到.
例如,由 (x1)2=2 可知 x1= 或 x1=,从而 x=1或 x=1,因此解集为 {1,1}.
探索新知
一元二次方程的解集
一般地,方程 (xk)2=t:
(1)当 t>0 时,解集为 ;
(2)当 t=0 时,解集为 ;
(3)当 t<0 时,解集为 .
{k,k+}
{k}
因此,对于一般的一元二次方程来说,只需要将其化为 (xk)2=t 的形式,就可得到方程的解集.
探索新知
尝试与发现
怎样将 x2+2x+3=0 化为 (x-k)2=t 的形式?动手试试看,并写出这个方程的解集.
我们知道,利用配方法可得
x2 + 2x + 3= x2 + 2x + 1+2 = (x + 1)2 + 2,
因此,x2+ 2x + 3=0 可以化为 (x +1)2 = -2,从而可知解集为 .
探索新知
事实上,利用配方法,总是可以将 ax2+bx+c=0 (a≠0) 化为 (x-k)2=t 的形式,过程如下:因为a≠0,所以
因此, ax2+bx+c=0 (a≠0) 可以化为
.
探索新知
一元二次方程的解集
从而可知,Δ=b2-4ac 的符号情况决定了上述方程的解集情况:
(1)当Δ=b2-4ac>0 时,方程的解集为
(2)当Δ=b2-4ac=0 时,方程的解集为
(3)当Δ=b2-4ac<0 时,方程的解集为 .
一般地,Δ=b2-4ac 称为一元二次方程 ax2+ bx+ c= 0 (a≠0)的判别式. 由此可知,一元二次方程解集的情况完全由它的系数决定.
例 1 求方程 的解集
典型例题
分析 这不是一个一元二次方程,但是通过把 看成一个整体就可以转化为一个一元二次方程.
解:设,则≥0,且原方程可变为 ,
因此可知 或 (舍).
从而 ,即 ,
所以原方程的解集为 .
探索新知
一元二次方程根与系数的关系
我们知道,一元二次方程 ax2+bx+c=0 (a≠0) 的解集不是空集时,这个方程的解可以记为
计算 x1+x2 和 x1x2 的值,并填空:
例 2 已知一元二次方程 2x2+3x-4=0 的两根为 x1 与 x2,求下列各式的值:
(1) x12+x22; (2) |x1-x2|.
典型例题
解:由一元二次方程根与系数的关系,得 x1+x2= ,x1x2=-2,
(1) 由上有 x12+x22=(x1+x2)2-2x1x2
=( )2-2×(-2)
(2) 因为(x1-x2)2=(x1+x2)2-4x1x2
=( )2-4×(-2)
所以 |x1-x2|= .
当堂检测
当堂检测
B
当堂检测
C
当堂检测
B
当堂检测
当堂检测
当堂检测
-1
-1
当堂检测
当堂检测
当堂检测
本节课学习了哪些知识点呢?
1.一元二次方程的解集;
2.一元二次方程根与系数的关系.
感谢观看
祝同学新学期新气象
