江苏省南京市六校联合体考试2024-2025学年高二下学期6月期末数学试卷(PDF版,含答案)
文档属性
| 名称 | 江苏省南京市六校联合体考试2024-2025学年高二下学期6月期末数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-27 19:32:47 | ||
图片预览




文档简介
2024-2025 学年高二第二学期六校联合体期末考试
高二数学
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.设集合 M={1,0,2a},N={1,a2},且 N M,则实数 a的值是 ( )
A. -2 B. 0 C. 1 D. 2
2.设 x∈R,则“cosx=1”是“sinx=0”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知 x>0,y>0,且 4x+y-xy=0,则 x+y的最小值为 ( )
A.8 B. 9 C.10 D. 11
x·cosx
4.函数 f(x)=
e|x
的图象大致为 ( )
|
A. B. C. D.
a b
5.行列式是近代数学中研究线性方程的有力工具,最简单的二阶行列式的运算定义如下: |c d|=ad
2a3 a3-a2
-bc,已知 Sn是等比数列{an}的前 n项和,若| a4 a3-a |=0,a1=1,q≠1,则 S7= ( )2
A.31 B.63 C.127 D.255
6.抛物线 C的顶点为坐标原点,焦点在 x轴上,直线 x=3交 C于 M,N两点,C的准线交 x轴于点 P,
若 PM⊥PN,则 C的方程为 ( )
A.y2=4x B.y2=6x C.y2=8x D.y2=12x
7.将各位数字之和为 6的三位数叫“幸运数”,比如 123,402,则所有“幸运数”的个数为 ( )
A.19 B.20 C.21 D.22
8.已知函数 f(x)及其导函数 f '(x)的定义域均为 R,记 g(x)=f '(x),已知 f(2x+1)和 g(x+2)都是偶函数,且
2025
g(2)=1,则 ∑ g(k)的值为 ( )
k=0
A.1 B.-1 C.2025 D.-2025
二、选择题:本大题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选项中,有多项
符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得 6分,部分选对得部分分,
不选或有错选的得 0分.
9.已知函数 f(x)=3sin(ωx π π- ),其中ω>0,且函数的两个相邻对称轴之间的距离为 ,则下列说法正确的是
6 2
( )
A.ω=2
B π.函数图象关于点( ,0)对称
24
C π.函数在区间[0, ]单调递增
6
D.函数的图象可以由 y=3sinωx π的图象向右平移 个单位得到
6
10.下列等式正确的是 ( )
10 10
A.∑C1k0=210 B.∑C2k=C311
k=1 k=2
10 10
C.∑(-1)kCk k 110=0 D.∑ =1-
k=1 k=1(k+1)! 11!
2 2
11.已知双曲线 C x y: - =1(a>0,b>0)的左、右焦点分别为 F
2 2 1
、F2,过 F2作斜率为
a b
- 15的直线与双曲线的右支交于 A、B两点(A在第一象限),|AB|=|BF1|,P为线段 AB的中点,O
为坐标原点,则下列说法正确的是 ( )
A.|AF1|=2|AF2| B.双曲线 C的离心率为 2
C.直线 OP 15的斜率为- D.△AF1F2的面积为 2 15a2
5
三、填空题:本大题共 3小题,每小题 5 分,共 15 分.请把答案填写在答题卡相应位置上.
12.圆 x2+y2=1与圆 x2+y2-6x-8y+9=0的公切线的条数是____▲____条.
— —
13.设 A 1 1,B是一个随机试验中的两个随机事件,且 P(A)= ,P(B)= ,P(A+B) 3= ,则 P(B|A)=___▲_____.
3 2 4
14.已知实数 x,y,z均小于 1,且满足 ex-elog23=e·(x-log23),ey-elog35=e·(y-log35),
ez-elog58=e·(z-log58),其中 e为自然对数的底数.则 x,y,z的大小关系是___▲____.
(用“<”连接)
四、解答题:本大题共 5 小题,共 77 分.请在答题卡指定区域内作答,解答时应写出必要的
文字说明,证明过程或演算步骤.
15.(本题满分 13分)
如图,在直三棱柱 ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E,F分别为 C1C,BC的中点.
(1)求证:A1B⊥B1C;
(2)求直线 A1B与平面 AEF所成角的余弦值.
16.(本题满分 15分)
某公司生产一种电子产品,每批产品进入市场之前,需要对其进行检测,现从某批产品中随机抽取 10
箱进行检测,其中有 6箱为一等品.
(1)现从这 10箱产品中随机抽取 3箱,求这三箱中恰有两箱是一等品的概率;
(2)用频率估计概率,在这批产品中随机抽取 3箱,用 X表示抽到一等品的箱数,求 X的分布列和数学
期望.
17.(本题满分 15分)
2 2
已知椭圆 C x y 1(a b 0) 3: + = > > 的离心率为 ,以椭圆的四个顶点为顶点的四边形的面积为 4.
a2 b2 2
(1)求椭圆 C的标准方程;
(2)记椭圆 C的左顶点为 A,右顶点为 B,过点 B作不垂直于坐标轴的直线 l交椭圆于另一点 G,过点 A
l H →BG 2→作 的垂线,垂足为 ,且 = BH,求直线 l的方程.
5
18.(本题满分 17分)
已知 f(x)=a·ex-x.
(1)求 f(x)在 x=0处的切线方程;
(2)求 f(x)的单调区间;
(3)若方程 a·ex-x=0有两个不相等的实数根 x1,x2,且 x1<x2,求证:(1-a)·x1>a.
19.(本题满分 17分)
已知数列{an}的前 n项和为 Sn,若存在常数λ(λ>0),使得λan≥Sn+1对任意 n∈N*都成立,则称数列{an}
具有性质 M(λ).
(1)若数列{an}的通项公式 an=-2n+1,求证:数列{an}具有性质 M(3);
(2)设数列{an}的各项均为正数,且{an}具有性质 M(λ).
①若数列{an}是公比为 q的等比数列,且λ=4,求 q的值;
②求λ的最小值.
2024-2025 学年高二第二学期六校联合体期末考试
高二数学参考答案
一、单选题
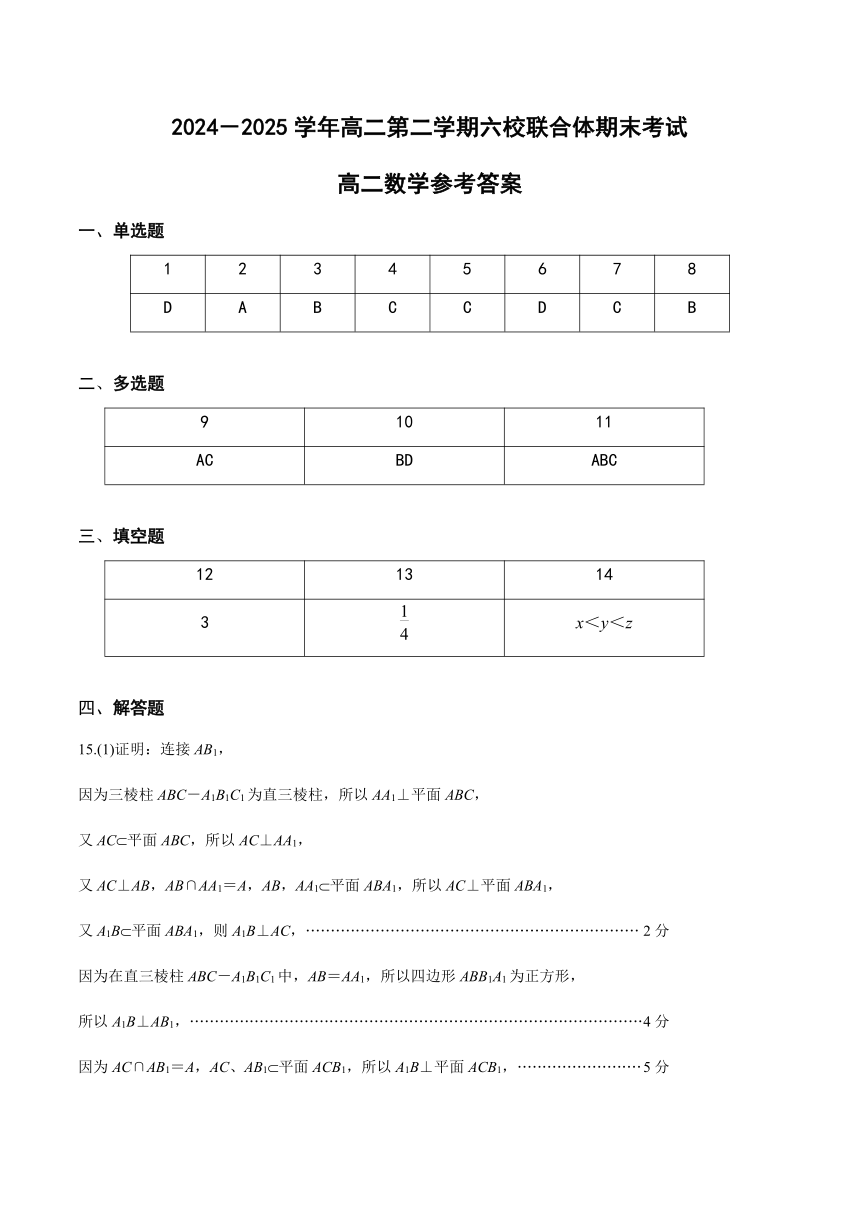
1 2 3 4 5 6 7 8
D A B C C D C B
二、多选题
9 10 11
AC BD ABC
三、填空题
12 13 14
1
3 4 x<y<z
四、解答题
15.(1)证明:连接 AB1,
因为三棱柱 ABC-A1B1C1为直三棱柱,所以 AA1⊥平面 ABC,
又 AC 平面 ABC,所以 AC⊥AA1,
又 AC⊥AB,AB∩AA1=A,AB,AA1 平面 ABA1,所以 AC⊥平面 ABA1,
又 A1B 平面 ABA1,则 A1B⊥AC,··································································· 2分
因为在直三棱柱 ABC-A1B1C1中,AB=AA1,所以四边形 ABB1A1为正方形,
所以 A1B⊥AB1,···························································································4分
因为 AC∩AB1=A,AC、AB1 平面 ACB1,所以 A1B⊥平面 ACB1,·························5分
又 B1C 平面 ACB1,则 A1B⊥B1C.·································································· 6分
(2)因为直三棱柱 ABC-A1B1C1中,∠BAC=90°,
所以 AB,AC,AA1两两垂直,
所以以 A为原点,分别以 AB,AC,AA1所在的直线为 x,y,z轴建立如图所示的空间直角坐标系,
则 A(0,0,0),A1(0,0,2),B(2,0,0),E(0,2,1),F(1,1,0),
→
所以A1B=(2,0,-2),················································································ 8分
→AE=(0,2,1) →,AF=(1,1,0).
n·→AE=2b+c=0
设平面 AEF的一个法向量为 n=(a,b,c),则
n·→
,
AF=a+b=0
令 a=1可得 n=(1,-1,2).······································································ 10分
设 A1B与平面 AEF所成角为θ,
|n·A→1B| 2
所以 sinθ=|cos<n → 3,A1B>|= = = ,······················12分→
|n||A1B| 4+4× 1+1+4 6
即 A1B与平面 AEF 3成角的正弦值为 ,
6
所以 A1B与平面 AEF
33
成角的余弦值为 .······················································13分
6
16.解:(1)记“这三箱中恰有两箱是一等品”为事件 A,·····································1分
C2 1P(A) 6C4 60 1则 = 3 = = .··············································································· 4分C10 120 2
(2) 6 3由题意,任取一个,取到一等品的概率为 = ,············································5分
10 5
3
因为 X可能的取值为 0,1,2,3,且 X服从二项分布(3, )
5
所以 P(X=0) 2=( )3 8= ,··············································································7分
5 125
P(X 1) C13·(2)2 36= = 3 = ,···············································································9分
5 5 125
P(X=2) C2(3= 3 )22 54= ,·············································································· 11分
5 5 125
P(X=3)=(3)3 27= ,···················································································13分
5 125
3 9
数学期望 E(X)=3× = .············································································ 15分
5 5
17.(1) 1由题意:S= ·2a·2b=4,所以 ab=2,····················································1分
2
c 3
又因为 = ,
a 2
所以 a=2,b=1,························································································3分
x2
所以椭圆的方程: +y2=1.········································································· 4分
4
(2)由题意,设直线 l的方程为 y=k(x-2),
y=k(x-2)
由 2 2 2 2x2 4y2 4 ,可得(1+4k )x -16k x+16k -4=0,+ =
2 16k
2 8k2-2 -4k
因为 +xG= ,所以 xG= ,代入直线方程可得 yG= .···················· 7分
1+4k2 1+4k2 1+4k2
(注:写出完整坐标或一个坐标分量都得 3分)
过点 B与 l 1垂直的直线方程为 y=- (x+2),
k
y 1=- (x+2)
k 2k2-2 -4k由 可得 xH= ,yH= ,··············································· 10分
y=k(x-2) k2+1 k2+1
(注:写出完整坐标或一个坐标分量都得 3分)
→
因为BG 2→ 2= BH,所以(xG-2,yG)= (xH-2,yH)
5 5
法一:x 2 2G- = (xH-2),·············································································· 11分
5
8k2-2 2 2k2-2
所以 -2= ·( -2),解得 k=±1,··················································13分
1+4k2 5 k2+1
所以直线 l的方程:y=x-2或 y=-x+2.····················································· 15分
2
法二:yG= yH,························································································· 11分
5
-4k 2 4k
所以 = ·(- ),解得 k=±1,························································· 13分
1+4k2 5 1+k2
所以直线 l的方程:y=x-2或 y=-x+2.····················································· 15分
y=k(x-2)
2
(注:如果先证一个结论:k 1AG·kBG=- ,因为 kBG=k k
1 1 8k -2 -4k, AG=- ,由
4 4k y=- (x+2)
可得 G( , ),
k 1+4k2 1+4k2
酌情给分)
18.(1)因为 f '(x)=a·ex-1,所以 f '(0)=a-1,···················································2分
又因为 f(0)=a,
所以 f(x)在 x=0处的切线方程为 y-a=(a-1)x,即 y=(a-1)x+a.·······················4分
(2)因为 f '(x)=a·ex-1,
①若 a≤0,则 f '(x)<0恒成立,所以 f(x)在(-∞,+∞)单调递减,无增区间.········ 7分
②若 a>0,令 f '(x)>0得 x>-lna,令 f '(x)<0得 x<-lna,所以 f(x)在(-∞,-lna)单调递减,在(-lna,
+∞)单调递增.························································································· 10分
(注:没写综上不扣分,a=0单独写不扣分,a=0漏掉扣 1分)
(3)若 a≤0,由(2)知 f(x)在(-∞,+∞)单调递减,方程至多有一个实根,不符题意,
所以 a>0.······························································································· 11分
x
法 1.由题意知 a·ex1=x1,所以 a
1
= x,且 x1 1>0.e
x
要证(1-a)x1>a,只要证(1-a)·ae
x1
>a x1 1 x1 x1,只要证(1-a)·e >1,只要证(1- x )·e >1,只要证 e -x1 1>1.e
··············································································································· 14分
令 g(x)=ex-x-1,x>0,g '(x)=ex-1>0,
所以 g(x)在(0,+∞)单调增,g(x)>g(0)=0,
因为 x x11>0,所以 g(x1)>0,即 e -x1>1,
所以(1-a)x1>a得证.················································································ 17分
法 2.由(2)得 f(x)在(-∞,-lna)单调递减,在(-lna,+∞)单调递增,
所以 f(-lna)=1+lna 1<0,所以 0<a< .
e
a a
因为 <1<-lna,所以 x1, ∈(-∞,-lna),
1-a 1-a
a a
要证(1-a)x1>a,只要证 x1> ,只要证 f(x1)<f( )
a
,只要证 f( )>0.
1-a 1-a 1-a
a a a
而 f( )=a·e a1-a- =a·(e 11-a- ),······················································ 14分
1-a 1-a 1-a
令 g(x)=ex-x-1,x>0,g '(x)=ex-1>0,
所以 g(x)在(0,+∞)单调增,g(x)>g(0)=0,
a a 1
所以 x>0时,ex-x-1>0恒成立,令 x= 得 e1-a- >0,
1-a 1-a
a
所以 f( )>0.
1-a
所以(1-a)x1>a得证.················································································ 17分
19.(1)设由数列{an}的通项公式,an=-2n+1,S
(-1-2n+1)n
n= =-n2,············ 2分
2
于是 3an-Sn+1=3(-2n+1)+(n+1)2=(n-2)2≥0,
即 3an≥Sn+1,
所以数列{an}具有性质 M(3).········································································· 4分
(2)①由数列{an}具有性质 M(4),得 4an≥Sn+1,又等比数列{an}的公比为 q,
若 q=1,则 4a1≥(n+1)a1,解得 n≤3,与 n为任意正整数相矛盾;·······················5分
n+1 n+1
当 q≠1时,4a1qn-1 a ·
1-q
≥ 1 ,而 a 0 4qn-1
1-q
n> ,整理得 ≥ ,
1-q 1-q
0 q 1 qn-1 1若 < < ,则 ≥ ,解得 n<1+log 1q ,与 n∈N*矛盾;················· 6分
(q-2)2 (q-2)2
n-1 n-1
若 q>1,则 q (q-2)2≤1,当 q=2时,q (q-2)2≤1恒成立,满足题意;···········7分
当 q>1且 q≠2时,qn-1 1 1≤ ,解得 n<1+logq ,与 n∈N*矛盾;··········· 8分
(q-2)2 (q-2)2
所以 q=2.·································································································9分
②由λan≥Sn+1,得λan+1≥Sn+2,即λ(Sn+1-Sn)≥Sn+2,··········································11分
因此λSn+1≥λSn+Sn+2≥2 λS S
Sn+2 λ Sn+1
n n+2,即 ≤ · ,············································13分
Sn+1 4 Sn
Sn+1 λ· Sn (λ)2·Sn-1 (λ)n-1则有 ≤ ≤ ≤…≤ ·S2,····················································· 15分
Sn 4 Sn-1 4 Sn-2 4 S1
λ n-1S λ n-1 S
由数列{an}各项均为正数,得 S 2n<Sn+1,从而 1<( ) ,即( ) > 1,4 S1 4 S2
若 0<λ<4,则 n 1 log S< + 1λ ,与 n∈N*矛盾,··················································16分
4S2
λ 4 (λ)n-1 1n-1 S1因此当 ≥ 时, ≥ > 恒成立,符合题意,
4 S2
所以λ的最小值为 4.··················································································· 17分
高二数学
一、选择题:本大题共 8 小题,每小题 5 分,共 40 分.在每小题给出的四个选项中,只有一
项是符合题目要求的,请把答案填涂在答题卡相应位置上.
1.设集合 M={1,0,2a},N={1,a2},且 N M,则实数 a的值是 ( )
A. -2 B. 0 C. 1 D. 2
2.设 x∈R,则“cosx=1”是“sinx=0”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
3.已知 x>0,y>0,且 4x+y-xy=0,则 x+y的最小值为 ( )
A.8 B. 9 C.10 D. 11
x·cosx
4.函数 f(x)=
e|x
的图象大致为 ( )
|
A. B. C. D.
a b
5.行列式是近代数学中研究线性方程的有力工具,最简单的二阶行列式的运算定义如下: |c d|=ad
2a3 a3-a2
-bc,已知 Sn是等比数列{an}的前 n项和,若| a4 a3-a |=0,a1=1,q≠1,则 S7= ( )2
A.31 B.63 C.127 D.255
6.抛物线 C的顶点为坐标原点,焦点在 x轴上,直线 x=3交 C于 M,N两点,C的准线交 x轴于点 P,
若 PM⊥PN,则 C的方程为 ( )
A.y2=4x B.y2=6x C.y2=8x D.y2=12x
7.将各位数字之和为 6的三位数叫“幸运数”,比如 123,402,则所有“幸运数”的个数为 ( )
A.19 B.20 C.21 D.22
8.已知函数 f(x)及其导函数 f '(x)的定义域均为 R,记 g(x)=f '(x),已知 f(2x+1)和 g(x+2)都是偶函数,且
2025
g(2)=1,则 ∑ g(k)的值为 ( )
k=0
A.1 B.-1 C.2025 D.-2025
二、选择题:本大题共 3 小题,每小题 6 分,共 18 分.在每小题给出的四个选项中,有多项
符合题目要求,请把答案填涂在答题卡相应位置上.全部选对得 6分,部分选对得部分分,
不选或有错选的得 0分.
9.已知函数 f(x)=3sin(ωx π π- ),其中ω>0,且函数的两个相邻对称轴之间的距离为 ,则下列说法正确的是
6 2
( )
A.ω=2
B π.函数图象关于点( ,0)对称
24
C π.函数在区间[0, ]单调递增
6
D.函数的图象可以由 y=3sinωx π的图象向右平移 个单位得到
6
10.下列等式正确的是 ( )
10 10
A.∑C1k0=210 B.∑C2k=C311
k=1 k=2
10 10
C.∑(-1)kCk k 110=0 D.∑ =1-
k=1 k=1(k+1)! 11!
2 2
11.已知双曲线 C x y: - =1(a>0,b>0)的左、右焦点分别为 F
2 2 1
、F2,过 F2作斜率为
a b
- 15的直线与双曲线的右支交于 A、B两点(A在第一象限),|AB|=|BF1|,P为线段 AB的中点,O
为坐标原点,则下列说法正确的是 ( )
A.|AF1|=2|AF2| B.双曲线 C的离心率为 2
C.直线 OP 15的斜率为- D.△AF1F2的面积为 2 15a2
5
三、填空题:本大题共 3小题,每小题 5 分,共 15 分.请把答案填写在答题卡相应位置上.
12.圆 x2+y2=1与圆 x2+y2-6x-8y+9=0的公切线的条数是____▲____条.
— —
13.设 A 1 1,B是一个随机试验中的两个随机事件,且 P(A)= ,P(B)= ,P(A+B) 3= ,则 P(B|A)=___▲_____.
3 2 4
14.已知实数 x,y,z均小于 1,且满足 ex-elog23=e·(x-log23),ey-elog35=e·(y-log35),
ez-elog58=e·(z-log58),其中 e为自然对数的底数.则 x,y,z的大小关系是___▲____.
(用“<”连接)
四、解答题:本大题共 5 小题,共 77 分.请在答题卡指定区域内作答,解答时应写出必要的
文字说明,证明过程或演算步骤.
15.(本题满分 13分)
如图,在直三棱柱 ABC-A1B1C1中,AB=AC=AA1=2,∠BAC=90°,E,F分别为 C1C,BC的中点.
(1)求证:A1B⊥B1C;
(2)求直线 A1B与平面 AEF所成角的余弦值.
16.(本题满分 15分)
某公司生产一种电子产品,每批产品进入市场之前,需要对其进行检测,现从某批产品中随机抽取 10
箱进行检测,其中有 6箱为一等品.
(1)现从这 10箱产品中随机抽取 3箱,求这三箱中恰有两箱是一等品的概率;
(2)用频率估计概率,在这批产品中随机抽取 3箱,用 X表示抽到一等品的箱数,求 X的分布列和数学
期望.
17.(本题满分 15分)
2 2
已知椭圆 C x y 1(a b 0) 3: + = > > 的离心率为 ,以椭圆的四个顶点为顶点的四边形的面积为 4.
a2 b2 2
(1)求椭圆 C的标准方程;
(2)记椭圆 C的左顶点为 A,右顶点为 B,过点 B作不垂直于坐标轴的直线 l交椭圆于另一点 G,过点 A
l H →BG 2→作 的垂线,垂足为 ,且 = BH,求直线 l的方程.
5
18.(本题满分 17分)
已知 f(x)=a·ex-x.
(1)求 f(x)在 x=0处的切线方程;
(2)求 f(x)的单调区间;
(3)若方程 a·ex-x=0有两个不相等的实数根 x1,x2,且 x1<x2,求证:(1-a)·x1>a.
19.(本题满分 17分)
已知数列{an}的前 n项和为 Sn,若存在常数λ(λ>0),使得λan≥Sn+1对任意 n∈N*都成立,则称数列{an}
具有性质 M(λ).
(1)若数列{an}的通项公式 an=-2n+1,求证:数列{an}具有性质 M(3);
(2)设数列{an}的各项均为正数,且{an}具有性质 M(λ).
①若数列{an}是公比为 q的等比数列,且λ=4,求 q的值;
②求λ的最小值.
2024-2025 学年高二第二学期六校联合体期末考试
高二数学参考答案
一、单选题
1 2 3 4 5 6 7 8
D A B C C D C B
二、多选题
9 10 11
AC BD ABC
三、填空题
12 13 14
1
3 4 x<y<z
四、解答题
15.(1)证明:连接 AB1,
因为三棱柱 ABC-A1B1C1为直三棱柱,所以 AA1⊥平面 ABC,
又 AC 平面 ABC,所以 AC⊥AA1,
又 AC⊥AB,AB∩AA1=A,AB,AA1 平面 ABA1,所以 AC⊥平面 ABA1,
又 A1B 平面 ABA1,则 A1B⊥AC,··································································· 2分
因为在直三棱柱 ABC-A1B1C1中,AB=AA1,所以四边形 ABB1A1为正方形,
所以 A1B⊥AB1,···························································································4分
因为 AC∩AB1=A,AC、AB1 平面 ACB1,所以 A1B⊥平面 ACB1,·························5分
又 B1C 平面 ACB1,则 A1B⊥B1C.·································································· 6分
(2)因为直三棱柱 ABC-A1B1C1中,∠BAC=90°,
所以 AB,AC,AA1两两垂直,
所以以 A为原点,分别以 AB,AC,AA1所在的直线为 x,y,z轴建立如图所示的空间直角坐标系,
则 A(0,0,0),A1(0,0,2),B(2,0,0),E(0,2,1),F(1,1,0),
→
所以A1B=(2,0,-2),················································································ 8分
→AE=(0,2,1) →,AF=(1,1,0).
n·→AE=2b+c=0
设平面 AEF的一个法向量为 n=(a,b,c),则
n·→
,
AF=a+b=0
令 a=1可得 n=(1,-1,2).······································································ 10分
设 A1B与平面 AEF所成角为θ,
|n·A→1B| 2
所以 sinθ=|cos<n → 3,A1B>|= = = ,······················12分→
|n||A1B| 4+4× 1+1+4 6
即 A1B与平面 AEF 3成角的正弦值为 ,
6
所以 A1B与平面 AEF
33
成角的余弦值为 .······················································13分
6
16.解:(1)记“这三箱中恰有两箱是一等品”为事件 A,·····································1分
C2 1P(A) 6C4 60 1则 = 3 = = .··············································································· 4分C10 120 2
(2) 6 3由题意,任取一个,取到一等品的概率为 = ,············································5分
10 5
3
因为 X可能的取值为 0,1,2,3,且 X服从二项分布(3, )
5
所以 P(X=0) 2=( )3 8= ,··············································································7分
5 125
P(X 1) C13·(2)2 36= = 3 = ,···············································································9分
5 5 125
P(X=2) C2(3= 3 )22 54= ,·············································································· 11分
5 5 125
P(X=3)=(3)3 27= ,···················································································13分
5 125
3 9
数学期望 E(X)=3× = .············································································ 15分
5 5
17.(1) 1由题意:S= ·2a·2b=4,所以 ab=2,····················································1分
2
c 3
又因为 = ,
a 2
所以 a=2,b=1,························································································3分
x2
所以椭圆的方程: +y2=1.········································································· 4分
4
(2)由题意,设直线 l的方程为 y=k(x-2),
y=k(x-2)
由 2 2 2 2x2 4y2 4 ,可得(1+4k )x -16k x+16k -4=0,+ =
2 16k
2 8k2-2 -4k
因为 +xG= ,所以 xG= ,代入直线方程可得 yG= .···················· 7分
1+4k2 1+4k2 1+4k2
(注:写出完整坐标或一个坐标分量都得 3分)
过点 B与 l 1垂直的直线方程为 y=- (x+2),
k
y 1=- (x+2)
k 2k2-2 -4k由 可得 xH= ,yH= ,··············································· 10分
y=k(x-2) k2+1 k2+1
(注:写出完整坐标或一个坐标分量都得 3分)
→
因为BG 2→ 2= BH,所以(xG-2,yG)= (xH-2,yH)
5 5
法一:x 2 2G- = (xH-2),·············································································· 11分
5
8k2-2 2 2k2-2
所以 -2= ·( -2),解得 k=±1,··················································13分
1+4k2 5 k2+1
所以直线 l的方程:y=x-2或 y=-x+2.····················································· 15分
2
法二:yG= yH,························································································· 11分
5
-4k 2 4k
所以 = ·(- ),解得 k=±1,························································· 13分
1+4k2 5 1+k2
所以直线 l的方程:y=x-2或 y=-x+2.····················································· 15分
y=k(x-2)
2
(注:如果先证一个结论:k 1AG·kBG=- ,因为 kBG=k k
1 1 8k -2 -4k, AG=- ,由
4 4k y=- (x+2)
可得 G( , ),
k 1+4k2 1+4k2
酌情给分)
18.(1)因为 f '(x)=a·ex-1,所以 f '(0)=a-1,···················································2分
又因为 f(0)=a,
所以 f(x)在 x=0处的切线方程为 y-a=(a-1)x,即 y=(a-1)x+a.·······················4分
(2)因为 f '(x)=a·ex-1,
①若 a≤0,则 f '(x)<0恒成立,所以 f(x)在(-∞,+∞)单调递减,无增区间.········ 7分
②若 a>0,令 f '(x)>0得 x>-lna,令 f '(x)<0得 x<-lna,所以 f(x)在(-∞,-lna)单调递减,在(-lna,
+∞)单调递增.························································································· 10分
(注:没写综上不扣分,a=0单独写不扣分,a=0漏掉扣 1分)
(3)若 a≤0,由(2)知 f(x)在(-∞,+∞)单调递减,方程至多有一个实根,不符题意,
所以 a>0.······························································································· 11分
x
法 1.由题意知 a·ex1=x1,所以 a
1
= x,且 x1 1>0.e
x
要证(1-a)x1>a,只要证(1-a)·ae
x1
>a x1 1 x1 x1,只要证(1-a)·e >1,只要证(1- x )·e >1,只要证 e -x1 1>1.e
··············································································································· 14分
令 g(x)=ex-x-1,x>0,g '(x)=ex-1>0,
所以 g(x)在(0,+∞)单调增,g(x)>g(0)=0,
因为 x x11>0,所以 g(x1)>0,即 e -x1>1,
所以(1-a)x1>a得证.················································································ 17分
法 2.由(2)得 f(x)在(-∞,-lna)单调递减,在(-lna,+∞)单调递增,
所以 f(-lna)=1+lna 1<0,所以 0<a< .
e
a a
因为 <1<-lna,所以 x1, ∈(-∞,-lna),
1-a 1-a
a a
要证(1-a)x1>a,只要证 x1> ,只要证 f(x1)<f( )
a
,只要证 f( )>0.
1-a 1-a 1-a
a a a
而 f( )=a·e a1-a- =a·(e 11-a- ),······················································ 14分
1-a 1-a 1-a
令 g(x)=ex-x-1,x>0,g '(x)=ex-1>0,
所以 g(x)在(0,+∞)单调增,g(x)>g(0)=0,
a a 1
所以 x>0时,ex-x-1>0恒成立,令 x= 得 e1-a- >0,
1-a 1-a
a
所以 f( )>0.
1-a
所以(1-a)x1>a得证.················································································ 17分
19.(1)设由数列{an}的通项公式,an=-2n+1,S
(-1-2n+1)n
n= =-n2,············ 2分
2
于是 3an-Sn+1=3(-2n+1)+(n+1)2=(n-2)2≥0,
即 3an≥Sn+1,
所以数列{an}具有性质 M(3).········································································· 4分
(2)①由数列{an}具有性质 M(4),得 4an≥Sn+1,又等比数列{an}的公比为 q,
若 q=1,则 4a1≥(n+1)a1,解得 n≤3,与 n为任意正整数相矛盾;·······················5分
n+1 n+1
当 q≠1时,4a1qn-1 a ·
1-q
≥ 1 ,而 a 0 4qn-1
1-q
n> ,整理得 ≥ ,
1-q 1-q
0 q 1 qn-1 1若 < < ,则 ≥ ,解得 n<1+log 1q ,与 n∈N*矛盾;················· 6分
(q-2)2 (q-2)2
n-1 n-1
若 q>1,则 q (q-2)2≤1,当 q=2时,q (q-2)2≤1恒成立,满足题意;···········7分
当 q>1且 q≠2时,qn-1 1 1≤ ,解得 n<1+logq ,与 n∈N*矛盾;··········· 8分
(q-2)2 (q-2)2
所以 q=2.·································································································9分
②由λan≥Sn+1,得λan+1≥Sn+2,即λ(Sn+1-Sn)≥Sn+2,··········································11分
因此λSn+1≥λSn+Sn+2≥2 λS S
Sn+2 λ Sn+1
n n+2,即 ≤ · ,············································13分
Sn+1 4 Sn
Sn+1 λ· Sn (λ)2·Sn-1 (λ)n-1则有 ≤ ≤ ≤…≤ ·S2,····················································· 15分
Sn 4 Sn-1 4 Sn-2 4 S1
λ n-1S λ n-1 S
由数列{an}各项均为正数,得 S 2n<Sn+1,从而 1<( ) ,即( ) > 1,4 S1 4 S2
若 0<λ<4,则 n 1 log S< + 1λ ,与 n∈N*矛盾,··················································16分
4S2
λ 4 (λ)n-1 1n-1 S1因此当 ≥ 时, ≥ > 恒成立,符合题意,
4 S2
所以λ的最小值为 4.··················································································· 17分
同课章节目录
