山东济南天桥区2024-2025学年七年级下学期数学期末考试试题(含答案)
文档属性
| 名称 | 山东济南天桥区2024-2025学年七年级下学期数学期末考试试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 480.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 15:48:00 | ||
图片预览


文档简介
2024—2025 学年第二学期七年级学业质量监测 数学试题(2025.06)
注意事项:
本试题共 8 页,满分为 150 分.考试时间为 120 分钟.
答卷前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上.
答选择题时,必须使用 2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;答非选择题时,用 0.5mm 黑色签字笔在答题卡上题号所提示的答题区域作答.答案写在试卷上无效.
第 Ⅰ 卷(选择题 共 40 分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.第 58 届世界乒乓球锦标赛于 2025 年 5 月 17 日至 25 日在卡塔尔多哈举办,我国乒乓球运动员在比赛中取得优异成绩,下列世乒赛标识中,是轴对称图形的是( )
2.我国在广东省江门市新建的中微子实验室主体部分将于 2025 年 8 月正式运行,中微子的空间范围至少是0.0000000062mm,数据0.0000000062mm用科学记数法可表示为( )
A. 62×10 8mm B. 6.2×109mm C. 6.2×10 9mm D. 0.62×10 8mm
3.下列运算中,正确的是( )
A. (x3)2=x6 B. x6÷x2=x3 C. 3x3 x2=x D. (3x)2=6x2
4.如图,为估计池塘两岸A、B间的距离,小明在池塘一侧选取了一点O,测得OA=16m,OB=12m,那么AB的距离不可能是( )
A. 5m B. 15m C. 20m D. 30m
5.有下列说法:①在同一平面内,两条直线的位置关系有平行、相交、垂直三种;②平面内,过一点有且只有一条直线与已知直线垂直;③过直线外一点有且只有一条直线与已知直线平行;④同角或等角的补角相等;其中正确的有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
6.某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
随着实验次数的增大,“盖面朝上” 的概率接近于(精确到 0.01)( )
A. 0.56 B. 0.54 C. 0.53 D. 0.5
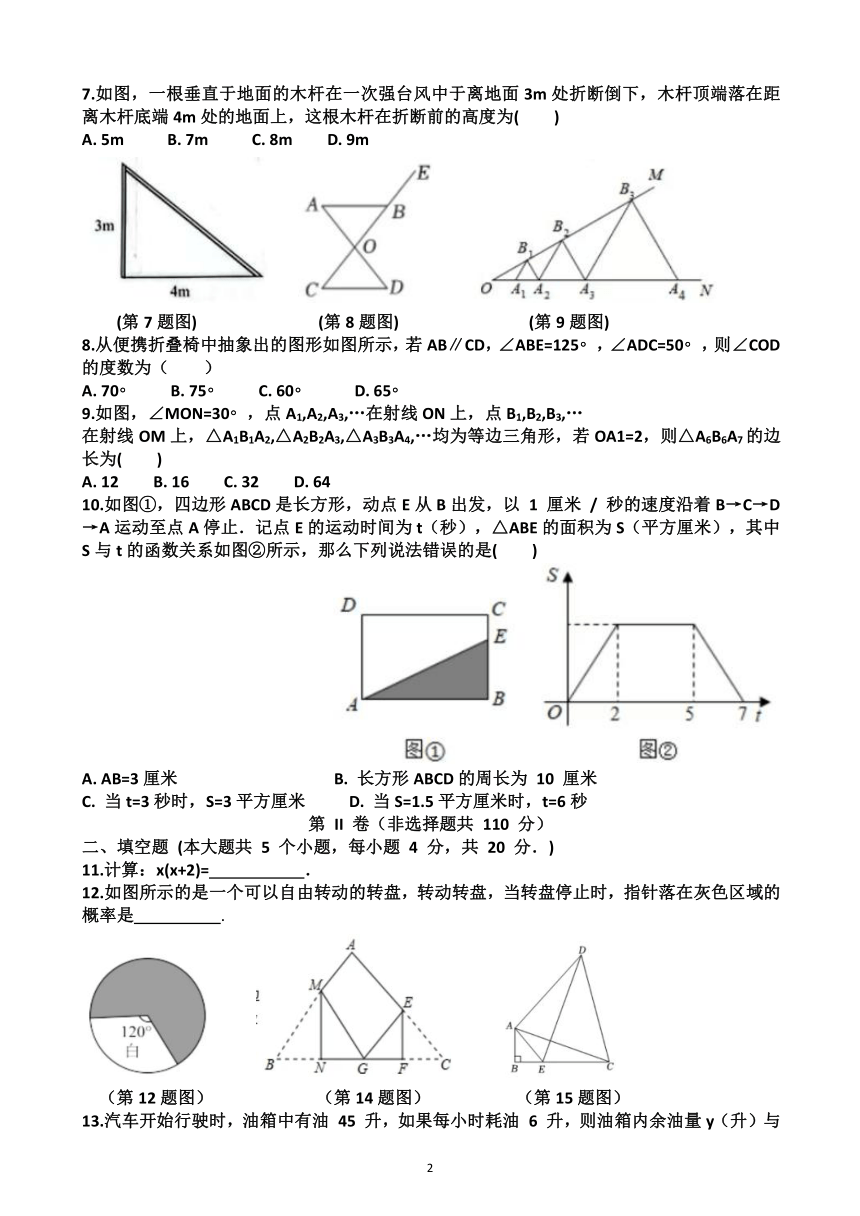
7.如图,一根垂直于地面的木杆在一次强台风中于离地面3m处折断倒下,木杆顶端落在距离木杆底端4m处的地面上,这根木杆在折断前的高度为( )
A. 5m B. 7m C. 8m D. 9m
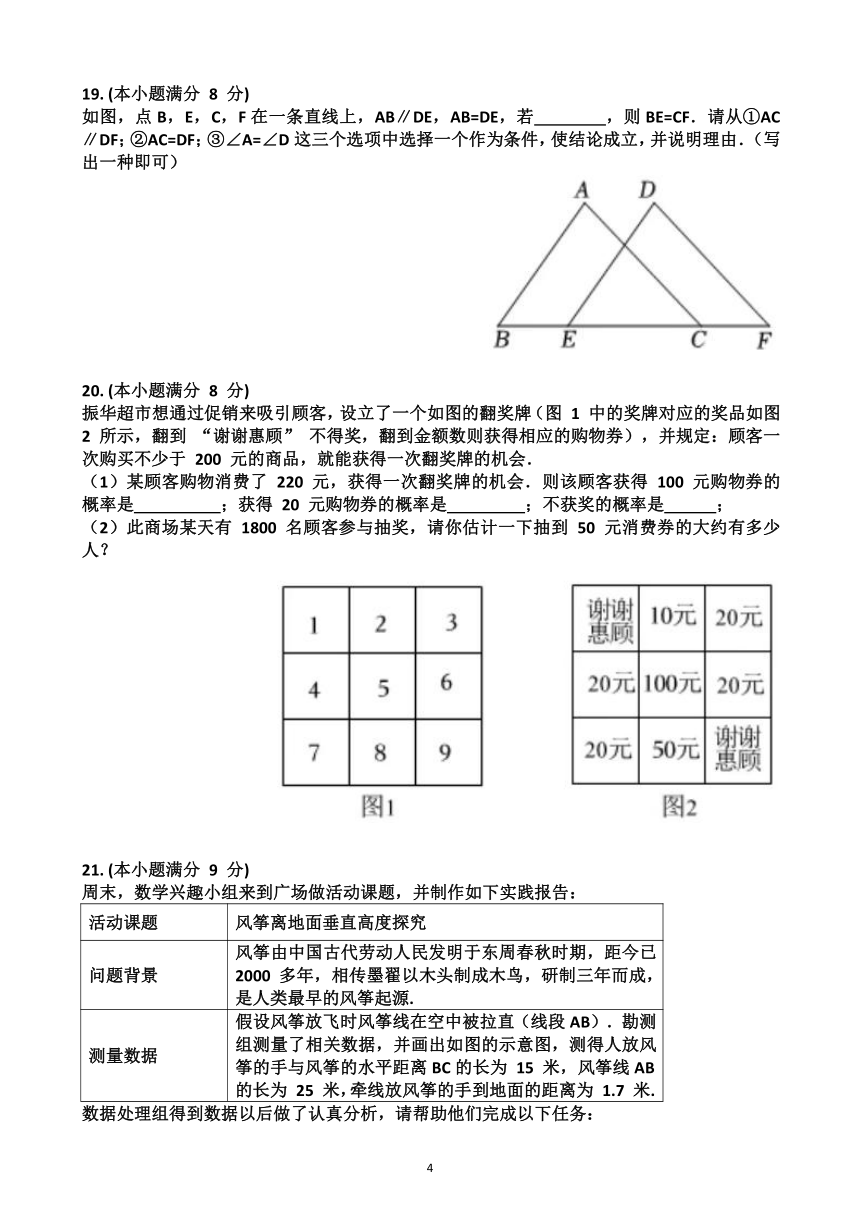
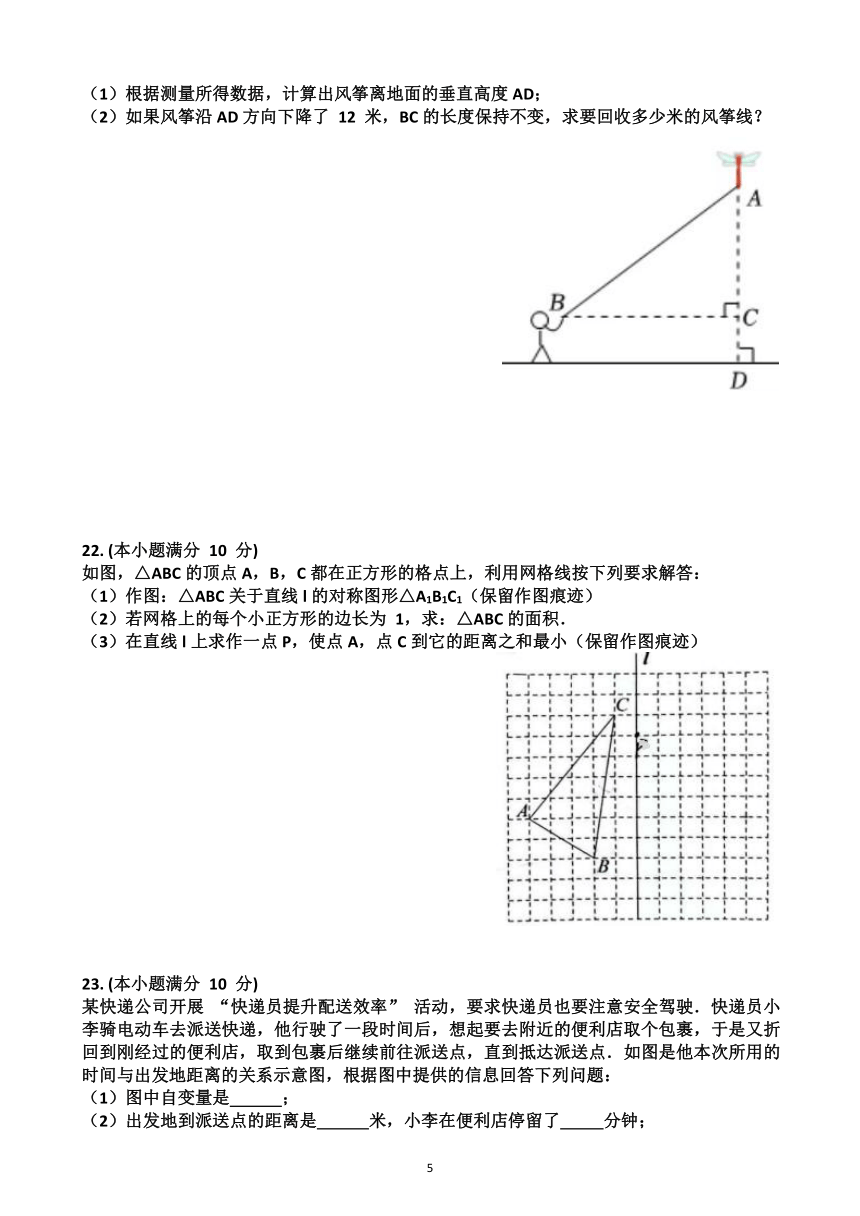
(第7题图) (第8题图) (第9题图)
8.从便携折叠椅中抽象出的图形如图所示,若AB∥CD,∠ABE=125 ,∠ADC=50 ,则∠COD的度数为( )
A. 70 B. 75 C. 60 D. 65
9.如图,∠MON=30 ,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…
在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A6B6A7的边长为( )
A. 12 B. 16 C. 32 D. 64
10.如图①,四边形ABCD是长方形,动点E从B出发,以 1 厘米 / 秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A. AB=3厘米 B. 长方形ABCD的周长为 10 厘米
C. 当t=3秒时,S=3平方厘米 D. 当S=1.5平方厘米时,t=6秒
第 II 卷(非选择题共 110 分)
二、填空题 (本大题共 5 个小题,每小题 4 分,共 20 分.)
11.计算:x(x+2)= .
12.如图所示的是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在灰色区域的概率是 .
(第12题图) (第14题图) (第15题图)
13.汽车开始行驶时,油箱中有油 45 升,如果每小时耗油 6 升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 .
14.如图,在△ABC中,将∠B和∠C按如图所示方式折叠,点B,C均落于边BC上一点G处,线段MN,EF为折痕,若∠A=80 ,则∠MGE= .
15.如图,在直角△ABC中,∠ABC=90 ,以AC为边作△ACD,满足AC=AD,点E为BC上一点,连接AE,DE,∠CAD=2∠BAE.有下列结论:①∠ACB=∠ADE;②AC⊥DE;③DE BE=BE+CE;④若CD∥AB,则AE⊥AD.其中正确结论的序号是 .
三.解答题 (本大题共 10 个小题,共 90 分.解答应写出文字说明,证明过程或演算步骤.)
16. (本小题满分 7 分)计算: 12025+( ) 1+∣ 4∣+(3.14 π)0 (+2)
17. (本小题满分 7 分)先化简,后求值:(x+3)(x 3) (x3 6x2)÷x,其中x=2
18. (本小题满分 7 分)已知直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30 ,∠1=60 ,求证:AB∥CD.请完成下面的证明过程:
证明:∵GH⊥CD(已知),
∴∠CHG= ( ).
又∵∠2=30 (已知),
∴∠3=∠CHG ∠2=60
∴∠4=60 ( )
又∵∠1=60 (已知),
∴∠1= ( )
∴AB∥ ( ).
19. (本小题满分 8 分)
如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,若 ,则BE=CF.请从①AC∥DF;②AC=DF;③∠A=∠D这三个选项中选择一个作为条件,使结论成立,并说明理由.(写出一种即可)
20. (本小题满分 8 分)
振华超市想通过促销来吸引顾客,设立了一个如图的翻奖牌(图 1 中的奖牌对应的奖品如图 2 所示,翻到 “谢谢惠顾” 不得奖,翻到金额数则获得相应的购物券),并规定:顾客一次购买不少于 200 元的商品,就能获得一次翻奖牌的机会.
(1)某顾客购物消费了 220 元,获得一次翻奖牌的机会.则该顾客获得 100 元购物券的概率是 ;获得 20 元购物券的概率是 ;不获奖的概率是 ;
(2)此商场某天有 1800 名顾客参与抽奖,请你估计一下抽到 50 元消费券的大约有多少人?
21. (本小题满分 9 分)
周末,数学兴趣小组来到广场做活动课题,并制作如下实践报告:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已 2000 多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.
测量数据 假设风筝放飞时风筝线在空中被拉直(线段AB).勘测组测量了相关数据,并画出如图的示意图,测得人放风筝的手与风筝的水平距离BC的长为 15 米,风筝线AB的长为 25 米,牵线放风筝的手到地面的距离为 1.7 米.
数据处理组得到数据以后做了认真分析,请帮助他们完成以下任务:
(1)根据测量所得数据,计算出风筝离地面的垂直高度AD;
(2)如果风筝沿AD方向下降了 12 米,BC的长度保持不变,求要回收多少米的风筝线?
22. (本小题满分 10 分)
如图,△ABC的顶点A,B,C都在正方形的格点上,利用网格线按下列要求解答:
(1)作图:△ABC关于直线l的对称图形△A1B1C1(保留作图痕迹)
(2)若网格上的每个小正方形的边长为 1,求:△ABC的面积.
(3)在直线l上求作一点P,使点A,点C到它的距离之和最小(保留作图痕迹)
23. (本小题满分 10 分)
某快递公司开展 “快递员提升配送效率” 活动,要求快递员也要注意安全驾驶.快递员小李骑电动车去派送快递,他行驶了一段时间后,想起要去附近的便利店取个包裹,于是又折回到刚经过的便利店,取到包裹后继续前往派送点,直到抵达派送点.如图是他本次所用的时间与出发地距离的关系示意图,根据图中提供的信息回答下列问题:
(1)图中自变量是 ;
(2)出发地到派送点的距离是 米,小李在便利店停留了 分钟;
(3)整个送快递的过程中,小李的最快速度是 米 / 分钟;
(4)当快递员小李距离派送点600米时,请直接写出小李所用时间.
24. (本小题满分 12 分)
数学课上,在复习 “三角形” 这一章时,老师提出如下问题:如图 1,在△ABC中,∠B>∠C,AD为∠BAC的角平分线,点F为角平分线上的一点并在AD(包括点A,不包括点D)上运动,过点F向边BC作垂线,垂足为E,请你猜想在点F运动过程中,∠B,∠C,∠DFE的数量关系,并说明理由.
(1)一组同学通过画图的方式探究点F运动到点A时的情况(如图 1),尝试改变∠B,∠C,具体的数值求∠DFE的值,对应值如下:
∠B/ 度 70 70 60 73
∠C/ 度 10 30 30 23
∠DFE/ 度 30 a 15 β
由表中数据可得,a= ,β= ;
(2)二组同学受到启发,开始研究点F在线段AD上(不包括端点A、D)运动时的情况(如图 2),很快发现了∠B,∠C,∠DFE之间的数量关系: ;
(3)三组同学提出:如果点F在直线AD上(不包括点A、D)运动(如图 3),∠B,∠C,∠DFE之间有什么样的数量关系呢?请你帮助他们解答并证明.
25. (本小题满分 12 分)
如图 1,在△ABC中,AC=BC,∠ACB=90°,若点E是AB延长线上一点,连接CE,以CE为腰作等腰直角三角形△CED,且∠DCE=90 ,CD=CE,连接BD.
(1)求证:△ACE≌△BCD;
(2)试说明:AE2+BE2=2CE2;
(3)如图 2,当点E是AB延长线上一点改成点E是直线AB上一点,其它条件不变,连接AD,若AC2=2,CD2=5,请直接写出AD2的值.
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.第 58 届世界乒乓球锦标赛于 2025 年 5 月 17 日至 25 日在卡塔尔多哈举办,我国乒乓球运动员在比赛中取得优异成绩,下列世乒赛标识中,是轴对称图形的是( A )
2.我国在广东省江门市新建的中微子实验室主体部分将于 2025 年 8 月正式运行,中微子的空间范围至少是0.0000000062mm,数据0.0000000062mm用科学记数法可表示为( C )
A. 62×10 8mm B. 6.2×109mm C. 6.2×10 9mm D. 0.62×10 8mm
3.下列运算中,正确的是( A )
A. (x3)2=x6 B. x6÷x2=x3 C. 3x3 x2=x D. (3x)2=6x2
4.如图,为估计池塘两岸A、B间的距离,小明在池塘一侧选取了一点O,测得OA=16m,OB=12m,那么AB的距离不可能是( D )
A. 5m B. 15m C. 20m D. 30m
5.有下列说法:①在同一平面内,两条直线的位置关系有平行、相交、垂直三种;②平面内,过一点有且只有一条直线与已知直线垂直;③过直线外一点有且只有一条直线与已知直线平行;④同角或等角的补角相等;其中正确的有( B )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
6.某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
随着实验次数的增大,“盖面朝上” 的概率接近于(精确到 0.01)( C )
A. 0.56 B. 0.54 C. 0.53 D. 0.5
7.如图,一根垂直于地面的木杆在一次强台风中于离地面3m处折断倒下,木杆顶端落在距离木杆底端4m处的地面上,这根木杆在折断前的高度为( C )
A. 5m B. 7m C. 8m D. 9m
(第7题图) (第8题图) (第9题图)
8.从便携折叠椅中抽象出的图形如图所示,若AB∥CD,∠ABE=125 ,∠ADC=50 ,则∠COD的度数为( B )
A. 70 B. 75 C. 60 D. 65
9.如图,∠MON=30 ,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…
在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A6B6A7的边长为( C )
A. 12 B. 16 C. 32 D. 64
10.如图①,四边形ABCD是长方形,动点E从B出发,以 1 厘米 / 秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( D )
A. AB=3厘米 B. 长方形ABCD的周长为 10 厘米
C. 当t=3秒时,S=3平方厘米 D. 当S=1.5平方厘米时,t=6秒
第 II 卷(非选择题共 110 分)
二、填空题 (本大题共 5 个小题,每小题 4 分,共 20 分.)
11.计算:x(x+2)= x2+2x .
12.如图所示的是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在灰色区域的概率是 .
(第12题图) (第14题图) (第15题图)
13.汽车开始行驶时,油箱中有油 45 升,如果每小时耗油 6 升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 y=45﹣6x .
14.如图,在△ABC中,将∠B和∠C按如图所示方式折叠,点B,C均落于边BC上一点G处,线段MN,EF为折痕,若∠A=80 ,则∠MGE= 80° .
15.如图,在直角△ABC中,∠ABC=90 ,以AC为边作△ACD,满足AC=AD,点E为BC上一点,连接AE,DE,∠CAD=2∠BAE.有下列结论:①∠ACB=∠ADE;②AC⊥DE;③DE BE=BE+CE;④若CD∥AB,则AE⊥AD.其中正确结论的序号是 ①③④ .
三.解答题 (本大题共 10 个小题,共 90 分.解答应写出文字说明,证明过程或演算步骤.)
16. (本小题满分 7 分)计算: 12025+( ) 1+∣ 4∣+(3.14 π)0 (+2)
=﹣1﹣2+4+1﹣2
= 0
17. (本小题满分 7 分)先化简,后求值:(x+3)(x 3) (x3 6x2)÷x,其中x=2
解原式=x2﹣9﹣x2+6x
=6x﹣9
将x=2代入得6×2﹣9=3
18. (本小题满分 7 分)已知直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30 ,∠1=60 ,求证:AB∥CD.请完成下面的证明过程:
证明:∵GH⊥CD(已知),
∴∠CHG= 90 ( 垂直的定义 ).
又∵∠2=30 (已知),
∴∠3=∠CHG ∠2=60
∴∠4=60 ( 对顶角相等 )
又∵∠1=60 (已知),
∴∠1= ∠4 ( 等量代换 )
∴AB∥ CD ( 同位角相等,两直线平行 ).
19. (本小题满分 8 分)
如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,若 ,则BE=CF.请从①AC∥DF;②AC=DF;③∠A=∠D这三个选项中选择一个作为条件,使结论成立,并说明理由.(写出一种即可)
选③
理由:∵AB∥DE
∴∠B=∠DEF
在△ABC和△DEF中
∴△ABC≌△DEF(ASA)
∴BC=EF
∴BC﹣EC=EF﹣EC
∴BE=CF
20. (本小题满分 8 分)
振华超市想通过促销来吸引顾客,设立了一个如图的翻奖牌(图 1 中的奖牌对应的奖品如图 2 所示,翻到 “谢谢惠顾” 不得奖,翻到金额数则获得相应的购物券),并规定:顾客一次购买不少于 200 元的商品,就能获得一次翻奖牌的机会.
(1)某顾客购物消费了 220 元,获得一次翻奖牌的机会.则该顾客获得 100 元购物券的概率是 ;获得 20 元购物券的概率是 ;不获奖的概率是 ;
(2)此商场某天有 1800 名顾客参与抽奖,请你估计一下抽到 50 元消费券的大约有多少人?
(1)
(2)1800×=200人
答:200人。
21. (本小题满分 9 分)
周末,数学兴趣小组来到广场做活动课题,并制作如下实践报告:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已 2000 多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.
测量数据 假设风筝放飞时风筝线在空中被拉直(线段AB).勘测组测量了相关数据,并画出如图的示意图,测得人放风筝的手与风筝的水平距离BC的长为 15 米,风筝线AB的长为 25 米,牵线放风筝的手到地面的距离为 1.7 米.
数据处理组得到数据以后做了认真分析,请帮助他们完成以下任务:
(1)根据测量所得数据,计算出风筝离地面的垂直高度AD;
(2)如果风筝沿AD方向下降了 12 米,BC的长度保持不变,求要回收多少米的风筝线?
∵∠ACB=90°,BC=15,AB=25
在 Rt△ABC 中,由勾股定理得,AC2=AB2-BC2
∴AC =20(米),则 AD = AC + CD =21.7米;
(2)如图,当风筝沿 AD 方向下降了12米时,. A'C=AC-A'A=20-12=8(米),
在 Rt△A'BC 中,由勾股定理得,
A'B2= A'C2+BC2
∴A'B =17(米)
∴25-17=8(米),
要回收8米的风筝线.
22. (本小题满分 10 分)
如图,△ABC的顶点A,B,C都在正方形的格点上,利用网格线按下列要求解答:
(1)作图:△ABC关于直线l的对称图形△A1B1C1(保留作图痕迹)
(2)若网格上的每个小正方形的边长为 1,求:△ABC的面积.
(3)在直线l上求作一点P,使点A,点C到它的距离之和最小(保留作图痕迹)
(1)略
(2)4×7﹣3×2÷2﹣4×5÷2﹣7×1÷2=11.5
(3)略
23. (本小题满分 10 分)
某快递公司开展 “快递员提升配送效率” 活动,要求快递员也要注意安全驾驶.快递员小李骑电动车去派送快递,他行驶了一段时间后,想起要去附近的便利店取个包裹,于是又折回到刚经过的便利店,取到包裹后继续前往派送点,直到抵达派送点.如图是他本次所用的时间与出发地距离的关系示意图,根据图中提供的信息回答下列问题:
(1)图中自变量是 时间 ;
(2)出发地到派送点的距离是 1500 米,小李在便利店停留了 4 分钟;
(3)整个送快递的过程中,小李的最快速度是 450 米 / 分钟;
(4)当快递员小李距离派送点600米时,请直接写出小李所用时间.
(1)时间
(2)1500 4
(3)450
(4)4.5分钟或7分钟或12分钟
24. (本小题满分 12 分)
数学课上,在复习 “三角形” 这一章时,老师提出如下问题:如图 1,在△ABC中,∠B>∠C,AD为∠BAC的角平分线,点F为角平分线上的一点并在AD(包括点A,不包括点D)上运动,过点F向边BC作垂线,垂足为E,请你猜想在点F运动过程中,∠B,∠C,∠DFE的数量关系,并说明理由.
(1)一组同学通过画图的方式探究点F运动到点A时的情况(如图 1),尝试改变∠B,∠C,具体的数值求∠DFE的值,对应值如下:
∠B/ 度 70 70 60 73
∠C/ 度 10 30 30 23
∠DFE/ 度 30 a 15 β
由表中数据可得,a= ,β= ;
(2)二组同学受到启发,开始研究点F在线段AD上(不包括端点A、D)运动时的情况(如图 2),很快发现了∠B,∠C,∠DFE之间的数量关系: ;
(3)三组同学提出:如果点F在直线AD上(不包括点A、D)运动(如图 3),∠B,∠C,∠DFE之间有什么样的数量关系呢?请你帮助他们解答并证明.
(1)a=10° β=25°
(2)2∠DFE=∠B+∠C
(3)2∠DFE=∠B+∠C
25. (本小题满分 12 分)
如图 1,在△ABC中,AC=BC,∠ACB=90°,若点E是AB延长线上一点,连接CE,以CE为腰作等腰直角三角形△CED,且∠DCE=90 ,CD=CE,连接BD.
(1)求证:△ACE≌△BCD;
(2)试说明:AE2+BE2=2CE2;
(3)如图 2,当点E是AB延长线上一点改成点E是直线AB上一点,其它条件不变,连接AD,若AC2=2,CD2=5,请直接写出AD2的值.
(1)∵∠ACB=90°,∠DCE=90°
∴∠ACB =∠DCE
∴∠ACB +∠BCE =∠DCE +∠BCE ,
即∠ACE =∠BCD ,
∵△CED是等腰直角三角形,且∠DCE =90°
∴CD = CE
在 △BCD 和△ACE 中,
∴△BCD≌△ACE ( SAS ),
∴BD = AE ;
(2)∵ AC = BC , LACB =90°,△CED 是等腰直角三角形,且∠DCE =90°
∴∠CAB =∠ABC =45°, CD = CE ,
∴DE2=CD2+CE2=2CE2
由(1)可知,△ BCD≌△ACE
∴BD = AE , ∠CBD =∠CAE =45°
∴∠ABD=∠ABC +∠CBD =45°+45°=90°
∴∠DBE =180°-90°=90°
∴BD2+BE2=DE2=2CE2
∴AE2+BE2=2CE2;
(3)13或3
注意事项:
本试题共 8 页,满分为 150 分.考试时间为 120 分钟.
答卷前,请考生务必将自己的姓名、座号和准考证号填写在答题卡上,并同时将考点、姓名、准考证号和座号填写在试卷规定的位置上.
答选择题时,必须使用 2B 铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号;答非选择题时,用 0.5mm 黑色签字笔在答题卡上题号所提示的答题区域作答.答案写在试卷上无效.
第 Ⅰ 卷(选择题 共 40 分)
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.第 58 届世界乒乓球锦标赛于 2025 年 5 月 17 日至 25 日在卡塔尔多哈举办,我国乒乓球运动员在比赛中取得优异成绩,下列世乒赛标识中,是轴对称图形的是( )
2.我国在广东省江门市新建的中微子实验室主体部分将于 2025 年 8 月正式运行,中微子的空间范围至少是0.0000000062mm,数据0.0000000062mm用科学记数法可表示为( )
A. 62×10 8mm B. 6.2×109mm C. 6.2×10 9mm D. 0.62×10 8mm
3.下列运算中,正确的是( )
A. (x3)2=x6 B. x6÷x2=x3 C. 3x3 x2=x D. (3x)2=6x2
4.如图,为估计池塘两岸A、B间的距离,小明在池塘一侧选取了一点O,测得OA=16m,OB=12m,那么AB的距离不可能是( )
A. 5m B. 15m C. 20m D. 30m
5.有下列说法:①在同一平面内,两条直线的位置关系有平行、相交、垂直三种;②平面内,过一点有且只有一条直线与已知直线垂直;③过直线外一点有且只有一条直线与已知直线平行;④同角或等角的补角相等;其中正确的有( )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
6.某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
随着实验次数的增大,“盖面朝上” 的概率接近于(精确到 0.01)( )
A. 0.56 B. 0.54 C. 0.53 D. 0.5
7.如图,一根垂直于地面的木杆在一次强台风中于离地面3m处折断倒下,木杆顶端落在距离木杆底端4m处的地面上,这根木杆在折断前的高度为( )
A. 5m B. 7m C. 8m D. 9m
(第7题图) (第8题图) (第9题图)
8.从便携折叠椅中抽象出的图形如图所示,若AB∥CD,∠ABE=125 ,∠ADC=50 ,则∠COD的度数为( )
A. 70 B. 75 C. 60 D. 65
9.如图,∠MON=30 ,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…
在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A6B6A7的边长为( )
A. 12 B. 16 C. 32 D. 64
10.如图①,四边形ABCD是长方形,动点E从B出发,以 1 厘米 / 秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( )
A. AB=3厘米 B. 长方形ABCD的周长为 10 厘米
C. 当t=3秒时,S=3平方厘米 D. 当S=1.5平方厘米时,t=6秒
第 II 卷(非选择题共 110 分)
二、填空题 (本大题共 5 个小题,每小题 4 分,共 20 分.)
11.计算:x(x+2)= .
12.如图所示的是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在灰色区域的概率是 .
(第12题图) (第14题图) (第15题图)
13.汽车开始行驶时,油箱中有油 45 升,如果每小时耗油 6 升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 .
14.如图,在△ABC中,将∠B和∠C按如图所示方式折叠,点B,C均落于边BC上一点G处,线段MN,EF为折痕,若∠A=80 ,则∠MGE= .
15.如图,在直角△ABC中,∠ABC=90 ,以AC为边作△ACD,满足AC=AD,点E为BC上一点,连接AE,DE,∠CAD=2∠BAE.有下列结论:①∠ACB=∠ADE;②AC⊥DE;③DE BE=BE+CE;④若CD∥AB,则AE⊥AD.其中正确结论的序号是 .
三.解答题 (本大题共 10 个小题,共 90 分.解答应写出文字说明,证明过程或演算步骤.)
16. (本小题满分 7 分)计算: 12025+( ) 1+∣ 4∣+(3.14 π)0 (+2)
17. (本小题满分 7 分)先化简,后求值:(x+3)(x 3) (x3 6x2)÷x,其中x=2
18. (本小题满分 7 分)已知直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30 ,∠1=60 ,求证:AB∥CD.请完成下面的证明过程:
证明:∵GH⊥CD(已知),
∴∠CHG= ( ).
又∵∠2=30 (已知),
∴∠3=∠CHG ∠2=60
∴∠4=60 ( )
又∵∠1=60 (已知),
∴∠1= ( )
∴AB∥ ( ).
19. (本小题满分 8 分)
如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,若 ,则BE=CF.请从①AC∥DF;②AC=DF;③∠A=∠D这三个选项中选择一个作为条件,使结论成立,并说明理由.(写出一种即可)
20. (本小题满分 8 分)
振华超市想通过促销来吸引顾客,设立了一个如图的翻奖牌(图 1 中的奖牌对应的奖品如图 2 所示,翻到 “谢谢惠顾” 不得奖,翻到金额数则获得相应的购物券),并规定:顾客一次购买不少于 200 元的商品,就能获得一次翻奖牌的机会.
(1)某顾客购物消费了 220 元,获得一次翻奖牌的机会.则该顾客获得 100 元购物券的概率是 ;获得 20 元购物券的概率是 ;不获奖的概率是 ;
(2)此商场某天有 1800 名顾客参与抽奖,请你估计一下抽到 50 元消费券的大约有多少人?
21. (本小题满分 9 分)
周末,数学兴趣小组来到广场做活动课题,并制作如下实践报告:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已 2000 多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.
测量数据 假设风筝放飞时风筝线在空中被拉直(线段AB).勘测组测量了相关数据,并画出如图的示意图,测得人放风筝的手与风筝的水平距离BC的长为 15 米,风筝线AB的长为 25 米,牵线放风筝的手到地面的距离为 1.7 米.
数据处理组得到数据以后做了认真分析,请帮助他们完成以下任务:
(1)根据测量所得数据,计算出风筝离地面的垂直高度AD;
(2)如果风筝沿AD方向下降了 12 米,BC的长度保持不变,求要回收多少米的风筝线?
22. (本小题满分 10 分)
如图,△ABC的顶点A,B,C都在正方形的格点上,利用网格线按下列要求解答:
(1)作图:△ABC关于直线l的对称图形△A1B1C1(保留作图痕迹)
(2)若网格上的每个小正方形的边长为 1,求:△ABC的面积.
(3)在直线l上求作一点P,使点A,点C到它的距离之和最小(保留作图痕迹)
23. (本小题满分 10 分)
某快递公司开展 “快递员提升配送效率” 活动,要求快递员也要注意安全驾驶.快递员小李骑电动车去派送快递,他行驶了一段时间后,想起要去附近的便利店取个包裹,于是又折回到刚经过的便利店,取到包裹后继续前往派送点,直到抵达派送点.如图是他本次所用的时间与出发地距离的关系示意图,根据图中提供的信息回答下列问题:
(1)图中自变量是 ;
(2)出发地到派送点的距离是 米,小李在便利店停留了 分钟;
(3)整个送快递的过程中,小李的最快速度是 米 / 分钟;
(4)当快递员小李距离派送点600米时,请直接写出小李所用时间.
24. (本小题满分 12 分)
数学课上,在复习 “三角形” 这一章时,老师提出如下问题:如图 1,在△ABC中,∠B>∠C,AD为∠BAC的角平分线,点F为角平分线上的一点并在AD(包括点A,不包括点D)上运动,过点F向边BC作垂线,垂足为E,请你猜想在点F运动过程中,∠B,∠C,∠DFE的数量关系,并说明理由.
(1)一组同学通过画图的方式探究点F运动到点A时的情况(如图 1),尝试改变∠B,∠C,具体的数值求∠DFE的值,对应值如下:
∠B/ 度 70 70 60 73
∠C/ 度 10 30 30 23
∠DFE/ 度 30 a 15 β
由表中数据可得,a= ,β= ;
(2)二组同学受到启发,开始研究点F在线段AD上(不包括端点A、D)运动时的情况(如图 2),很快发现了∠B,∠C,∠DFE之间的数量关系: ;
(3)三组同学提出:如果点F在直线AD上(不包括点A、D)运动(如图 3),∠B,∠C,∠DFE之间有什么样的数量关系呢?请你帮助他们解答并证明.
25. (本小题满分 12 分)
如图 1,在△ABC中,AC=BC,∠ACB=90°,若点E是AB延长线上一点,连接CE,以CE为腰作等腰直角三角形△CED,且∠DCE=90 ,CD=CE,连接BD.
(1)求证:△ACE≌△BCD;
(2)试说明:AE2+BE2=2CE2;
(3)如图 2,当点E是AB延长线上一点改成点E是直线AB上一点,其它条件不变,连接AD,若AC2=2,CD2=5,请直接写出AD2的值.
答案
一、选择题(本大题共 10 个小题,每小题 4 分,共 40 分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.第 58 届世界乒乓球锦标赛于 2025 年 5 月 17 日至 25 日在卡塔尔多哈举办,我国乒乓球运动员在比赛中取得优异成绩,下列世乒赛标识中,是轴对称图形的是( A )
2.我国在广东省江门市新建的中微子实验室主体部分将于 2025 年 8 月正式运行,中微子的空间范围至少是0.0000000062mm,数据0.0000000062mm用科学记数法可表示为( C )
A. 62×10 8mm B. 6.2×109mm C. 6.2×10 9mm D. 0.62×10 8mm
3.下列运算中,正确的是( A )
A. (x3)2=x6 B. x6÷x2=x3 C. 3x3 x2=x D. (3x)2=6x2
4.如图,为估计池塘两岸A、B间的距离,小明在池塘一侧选取了一点O,测得OA=16m,OB=12m,那么AB的距离不可能是( D )
A. 5m B. 15m C. 20m D. 30m
5.有下列说法:①在同一平面内,两条直线的位置关系有平行、相交、垂直三种;②平面内,过一点有且只有一条直线与已知直线垂直;③过直线外一点有且只有一条直线与已知直线平行;④同角或等角的补角相等;其中正确的有( B )
A. 4 个 B. 3 个 C. 2 个 D. 1 个
6.某学习小组做抛掷一枚瓶盖的实验,整理的实验数据如表:
随着实验次数的增大,“盖面朝上” 的概率接近于(精确到 0.01)( C )
A. 0.56 B. 0.54 C. 0.53 D. 0.5
7.如图,一根垂直于地面的木杆在一次强台风中于离地面3m处折断倒下,木杆顶端落在距离木杆底端4m处的地面上,这根木杆在折断前的高度为( C )
A. 5m B. 7m C. 8m D. 9m
(第7题图) (第8题图) (第9题图)
8.从便携折叠椅中抽象出的图形如图所示,若AB∥CD,∠ABE=125 ,∠ADC=50 ,则∠COD的度数为( B )
A. 70 B. 75 C. 60 D. 65
9.如图,∠MON=30 ,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…
在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA1=2,则△A6B6A7的边长为( C )
A. 12 B. 16 C. 32 D. 64
10.如图①,四边形ABCD是长方形,动点E从B出发,以 1 厘米 / 秒的速度沿着B→C→D→A运动至点A停止.记点E的运动时间为t(秒),△ABE的面积为S(平方厘米),其中S与t的函数关系如图②所示,那么下列说法错误的是( D )
A. AB=3厘米 B. 长方形ABCD的周长为 10 厘米
C. 当t=3秒时,S=3平方厘米 D. 当S=1.5平方厘米时,t=6秒
第 II 卷(非选择题共 110 分)
二、填空题 (本大题共 5 个小题,每小题 4 分,共 20 分.)
11.计算:x(x+2)= x2+2x .
12.如图所示的是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在灰色区域的概率是 .
(第12题图) (第14题图) (第15题图)
13.汽车开始行驶时,油箱中有油 45 升,如果每小时耗油 6 升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 y=45﹣6x .
14.如图,在△ABC中,将∠B和∠C按如图所示方式折叠,点B,C均落于边BC上一点G处,线段MN,EF为折痕,若∠A=80 ,则∠MGE= 80° .
15.如图,在直角△ABC中,∠ABC=90 ,以AC为边作△ACD,满足AC=AD,点E为BC上一点,连接AE,DE,∠CAD=2∠BAE.有下列结论:①∠ACB=∠ADE;②AC⊥DE;③DE BE=BE+CE;④若CD∥AB,则AE⊥AD.其中正确结论的序号是 ①③④ .
三.解答题 (本大题共 10 个小题,共 90 分.解答应写出文字说明,证明过程或演算步骤.)
16. (本小题满分 7 分)计算: 12025+( ) 1+∣ 4∣+(3.14 π)0 (+2)
=﹣1﹣2+4+1﹣2
= 0
17. (本小题满分 7 分)先化简,后求值:(x+3)(x 3) (x3 6x2)÷x,其中x=2
解原式=x2﹣9﹣x2+6x
=6x﹣9
将x=2代入得6×2﹣9=3
18. (本小题满分 7 分)已知直线AB,CD被直线EF所截,点H为CD与EF的交点,GH⊥CD于点H,∠2=30 ,∠1=60 ,求证:AB∥CD.请完成下面的证明过程:
证明:∵GH⊥CD(已知),
∴∠CHG= 90 ( 垂直的定义 ).
又∵∠2=30 (已知),
∴∠3=∠CHG ∠2=60
∴∠4=60 ( 对顶角相等 )
又∵∠1=60 (已知),
∴∠1= ∠4 ( 等量代换 )
∴AB∥ CD ( 同位角相等,两直线平行 ).
19. (本小题满分 8 分)
如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,若 ,则BE=CF.请从①AC∥DF;②AC=DF;③∠A=∠D这三个选项中选择一个作为条件,使结论成立,并说明理由.(写出一种即可)
选③
理由:∵AB∥DE
∴∠B=∠DEF
在△ABC和△DEF中
∴△ABC≌△DEF(ASA)
∴BC=EF
∴BC﹣EC=EF﹣EC
∴BE=CF
20. (本小题满分 8 分)
振华超市想通过促销来吸引顾客,设立了一个如图的翻奖牌(图 1 中的奖牌对应的奖品如图 2 所示,翻到 “谢谢惠顾” 不得奖,翻到金额数则获得相应的购物券),并规定:顾客一次购买不少于 200 元的商品,就能获得一次翻奖牌的机会.
(1)某顾客购物消费了 220 元,获得一次翻奖牌的机会.则该顾客获得 100 元购物券的概率是 ;获得 20 元购物券的概率是 ;不获奖的概率是 ;
(2)此商场某天有 1800 名顾客参与抽奖,请你估计一下抽到 50 元消费券的大约有多少人?
(1)
(2)1800×=200人
答:200人。
21. (本小题满分 9 分)
周末,数学兴趣小组来到广场做活动课题,并制作如下实践报告:
活动课题 风筝离地面垂直高度探究
问题背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已 2000 多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.
测量数据 假设风筝放飞时风筝线在空中被拉直(线段AB).勘测组测量了相关数据,并画出如图的示意图,测得人放风筝的手与风筝的水平距离BC的长为 15 米,风筝线AB的长为 25 米,牵线放风筝的手到地面的距离为 1.7 米.
数据处理组得到数据以后做了认真分析,请帮助他们完成以下任务:
(1)根据测量所得数据,计算出风筝离地面的垂直高度AD;
(2)如果风筝沿AD方向下降了 12 米,BC的长度保持不变,求要回收多少米的风筝线?
∵∠ACB=90°,BC=15,AB=25
在 Rt△ABC 中,由勾股定理得,AC2=AB2-BC2
∴AC =20(米),则 AD = AC + CD =21.7米;
(2)如图,当风筝沿 AD 方向下降了12米时,. A'C=AC-A'A=20-12=8(米),
在 Rt△A'BC 中,由勾股定理得,
A'B2= A'C2+BC2
∴A'B =17(米)
∴25-17=8(米),
要回收8米的风筝线.
22. (本小题满分 10 分)
如图,△ABC的顶点A,B,C都在正方形的格点上,利用网格线按下列要求解答:
(1)作图:△ABC关于直线l的对称图形△A1B1C1(保留作图痕迹)
(2)若网格上的每个小正方形的边长为 1,求:△ABC的面积.
(3)在直线l上求作一点P,使点A,点C到它的距离之和最小(保留作图痕迹)
(1)略
(2)4×7﹣3×2÷2﹣4×5÷2﹣7×1÷2=11.5
(3)略
23. (本小题满分 10 分)
某快递公司开展 “快递员提升配送效率” 活动,要求快递员也要注意安全驾驶.快递员小李骑电动车去派送快递,他行驶了一段时间后,想起要去附近的便利店取个包裹,于是又折回到刚经过的便利店,取到包裹后继续前往派送点,直到抵达派送点.如图是他本次所用的时间与出发地距离的关系示意图,根据图中提供的信息回答下列问题:
(1)图中自变量是 时间 ;
(2)出发地到派送点的距离是 1500 米,小李在便利店停留了 4 分钟;
(3)整个送快递的过程中,小李的最快速度是 450 米 / 分钟;
(4)当快递员小李距离派送点600米时,请直接写出小李所用时间.
(1)时间
(2)1500 4
(3)450
(4)4.5分钟或7分钟或12分钟
24. (本小题满分 12 分)
数学课上,在复习 “三角形” 这一章时,老师提出如下问题:如图 1,在△ABC中,∠B>∠C,AD为∠BAC的角平分线,点F为角平分线上的一点并在AD(包括点A,不包括点D)上运动,过点F向边BC作垂线,垂足为E,请你猜想在点F运动过程中,∠B,∠C,∠DFE的数量关系,并说明理由.
(1)一组同学通过画图的方式探究点F运动到点A时的情况(如图 1),尝试改变∠B,∠C,具体的数值求∠DFE的值,对应值如下:
∠B/ 度 70 70 60 73
∠C/ 度 10 30 30 23
∠DFE/ 度 30 a 15 β
由表中数据可得,a= ,β= ;
(2)二组同学受到启发,开始研究点F在线段AD上(不包括端点A、D)运动时的情况(如图 2),很快发现了∠B,∠C,∠DFE之间的数量关系: ;
(3)三组同学提出:如果点F在直线AD上(不包括点A、D)运动(如图 3),∠B,∠C,∠DFE之间有什么样的数量关系呢?请你帮助他们解答并证明.
(1)a=10° β=25°
(2)2∠DFE=∠B+∠C
(3)2∠DFE=∠B+∠C
25. (本小题满分 12 分)
如图 1,在△ABC中,AC=BC,∠ACB=90°,若点E是AB延长线上一点,连接CE,以CE为腰作等腰直角三角形△CED,且∠DCE=90 ,CD=CE,连接BD.
(1)求证:△ACE≌△BCD;
(2)试说明:AE2+BE2=2CE2;
(3)如图 2,当点E是AB延长线上一点改成点E是直线AB上一点,其它条件不变,连接AD,若AC2=2,CD2=5,请直接写出AD2的值.
(1)∵∠ACB=90°,∠DCE=90°
∴∠ACB =∠DCE
∴∠ACB +∠BCE =∠DCE +∠BCE ,
即∠ACE =∠BCD ,
∵△CED是等腰直角三角形,且∠DCE =90°
∴CD = CE
在 △BCD 和△ACE 中,
∴△BCD≌△ACE ( SAS ),
∴BD = AE ;
(2)∵ AC = BC , LACB =90°,△CED 是等腰直角三角形,且∠DCE =90°
∴∠CAB =∠ABC =45°, CD = CE ,
∴DE2=CD2+CE2=2CE2
由(1)可知,△ BCD≌△ACE
∴BD = AE , ∠CBD =∠CAE =45°
∴∠ABD=∠ABC +∠CBD =45°+45°=90°
∴∠DBE =180°-90°=90°
∴BD2+BE2=DE2=2CE2
∴AE2+BE2=2CE2;
(3)13或3
同课章节目录
