2025年宁夏吴忠市中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年宁夏吴忠市中考数学模拟试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 187.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 00:00:00 | ||
图片预览



文档简介
2025年宁夏吴忠市中考数学模拟试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,点和点表示的数分别为和,下列式子中正确的是( )
A. B. C. D.
2.下列所给图形是中心对称图形也是轴对称图形的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.年月日,搭载神舟十八号载人飞船的长征二号遥十八运载火箭成功发射为了培养青少年对航天知识学习的兴趣,某校开展航天知识竞赛活动经过几轮筛选,八年级班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛经过统计,四名同学成绩的平均数单位:分及方差如下表所示.
甲 乙 丙 丁
平均数
方差
要选一名成绩好且状态稳定的同学参赛,应选择( )
A. 甲 B. 乙 C. 丙 D. 丁
5.如图,已知直线,将一块含的直角三角板按如图方式放置,其中点,分别落在直线、上若,则等于( )
A. B.
C. D.
6.如图,是的直径,若,则的度数是( )
A. B.
C. D.
7.如图,一次函数与的图象相交于点,则关于的不等式的解集是( )
A.
B.
C.
D.
8.如图,点是正九边形的中心,连接,,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共8小题,每小题3分,共24分。
9.若代数式在实数范围内有意义,则实数的取值范围是 .
10.一种袋装食品标准净重为克,质监部门工作人员为了解该种食品每袋重与标准净重的误差,把食品净重克记为克,那么,食品净重克就记为______克
11.中国传统文化中的“四瑞兽”是古代象征样瑞与方位的神兽,分别为:青龙、白虎、朱雀、玄武小王和小李在美术课上都想从“四瑞兽”中随机选择一个瑞兽进行绘画创作,他们所选瑞兽相同的概率是______.
12.如图,为的切线,点为切点,交于点,点在上,连接、,,若,则的度数为______
13.定义一种法则“”如下:,例如:,若,则的取值范围是______.
14.若关于的方程的一个根是,则另一个根是______.
15.如图,是反比例函数的图象上的一个动点,作点关于原点的对称点,以为斜边作等腰直角三角形,若点的坐标为,则______.
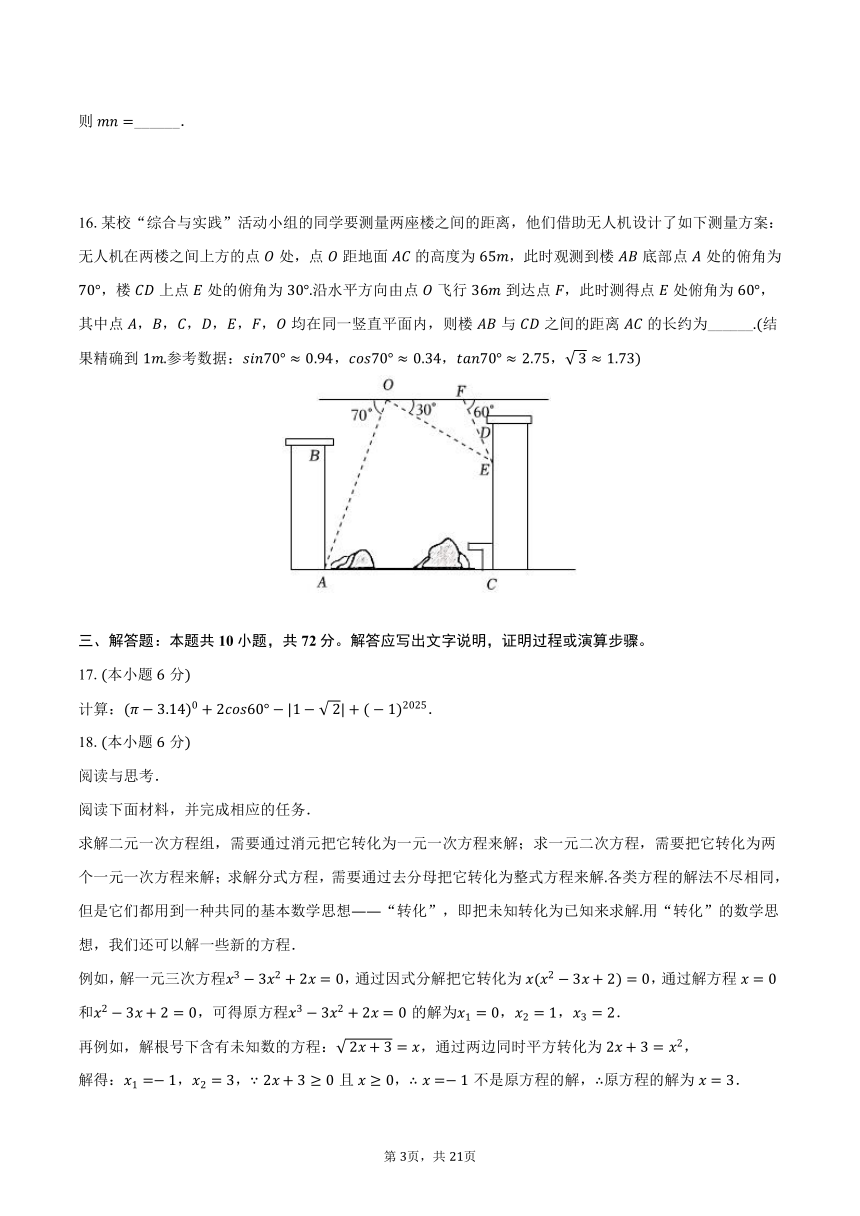
16.某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点处,点距地面的高度为,此时观测到楼底部点处的俯角为,楼上点处的俯角为沿水平方向由点飞行到达点,此时测得点处俯角为,其中点,,,,,,均在同一竖直平面内,则楼与之间的距离的长约为______结果精确到参考数据:,,,
三、解答题:本题共10小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
阅读与思考.
阅读下面材料,并完成相应的任务.
求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求一元二次方程,需要把它转化为两个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想“转化”,即把未知转化为已知来求解用“转化”的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程,通过因式分解把它转化为,通过解方程和,可得原方程的解为,,.
再例如,解根号下含有未知数的方程:,通过两边同时平方转化为,
解得:,,且,不是原方程的解,原方程的解为.
请仔细阅读材料,解下列方程:
解方程:;
解方程:.
19.本小题分
如图,平行四边形中,点在的延长线上,点在的延长线上,满足,连接、连接,分别与,交于点,,且平分.
求证:四边形是菱形;
若,,求四边形的面积.
20.本小题分
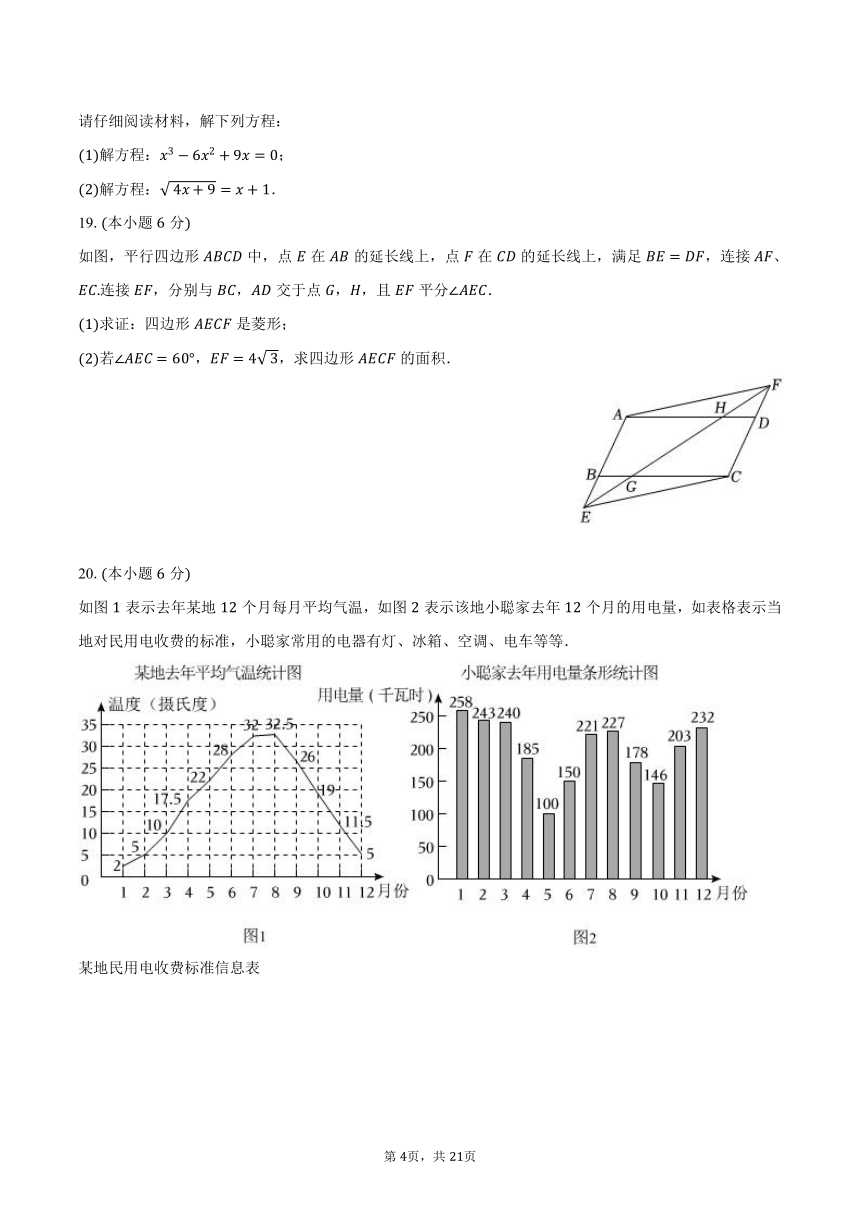
如图表示去年某地个月每月平均气温,如图表示该地小聪家去年个月的用电量,如表格表示当地对民用电收费的标准,小聪家常用的电器有灯、冰箱、空调、电车等等.
某地民用电收费标准信息表
月用电量 居民峰谷分时电价
高峰时段电价
::
单位:元 低谷时段电价
::以外
单位:元
千瓦时以下
千瓦时
千瓦时及以上
根据图求出个月中用电量的中位数以及超过千瓦时月份的月平均用电量.
根据统计图与信息表,请描述月用电量与气温间的一些关系,并对家庭用电提出一些建议.
21.本小题分
如图,在矩形中,为上一点,将沿翻折,点落在点处,延长交边于点,过点作分别交,于点,.
当时,若点恰好为的中点,求出,的值.
小明想探究在点运动的过程中,,,之间的数量关系,记,,,在的基础上,他通过几何画板画图,度量,得到以下几组对应值如表格所示,根据数据,请猜想,,三个量的关系以及,之间的数量关系,并说明理由.
如图,过点作分别交,于点,若,,求的值用表示.
22.本小题分
小明家饮水机中原有水的温度为,通电开机后,饮水机自动开始加热此过程中水温与开机时间分满足一次函数关系,当加热到时自动停止加热,随后水温开始下降此过程中水温与开机时间分成反比例关系,当水温降至时,饮水机又自动开始加热,重复上述程序如图所示,根据图中提供的信息,解答下列问题:
求图中的值;
若小明在通电开机后即外出散步,请你预测小明散步分钟回到家时,饮水机内的温度约为多少?
23.本小题分
某企业信息部对,两种产品进行市场调研,数据信息分析如下:
信息:如果单独投资种产品,所获利润万元与投资金额,单位:万元之间存在如图所示的关系;
信息:如果单独投资种产品,则所获利润万元与投资金额万元之间存在如表所示的关系:
万元
万元
求出与的函数关系式;
从所学过的一次函数、二次函数或反比例函数中选择一种适当函数模型,模拟种产品所获利润的变化趋势请说明选择该模型的理由,并求出与的函数表达式;
如果该企业同时对、两种产品共投资万元,请设计一个能获得最大利润的投资方案,并求出按此方案所获得的最大利润.
24.本小题分
如图,在中,直径弦于点,连接,,过点作交于点,过点作交的延长线于点.
求证:是的切线;
若,,求的长.
25.本小题分
如图,在平面直角坐标系中,抛物线与轴交于点,,交轴于点,且.
求该抛物线的函数表达式;
如图,点为直线上方抛物线上的一动点,过点作交于点,,为轴上的动点,在的下方,满足,连接,,当取得最大值时,求点的坐标及的最小值;
将抛物线沿着射线方向平移个单位长度得到新抛物线,在当取得最大值的条件下,点为新抛物线上一点,连接,,当时,请直接写出点的横坐标.
26.本小题分
如图,在与中,,,,点在直线上,连接.
若,求证:≌;
如图,连接,点为线段中点,点为线段中点,连接求证:;
如图,若,,连接,点为线段中点,当点在的延长线上运动时,请直接写出:线段的最小值______.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
8.【答案】
9.【答案】且
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】.
【解析】解:原式
.
18.【解析】,
,
.
或.
,.
,
两边平方,得,
整理,得.
.
,.
且,
不是原方程的解.
原方程的解为.
19.【解析】证明:是平行四边形,
,,
,
,即,
且,即,
四边形是平行四边形,
又且平分,
,,
,
,
平行四边形是菱形;
解:如图,连接交于点,
四边形是菱形,
,
,
,且,
,
,,
,
在中,,,
,
,
,
,
.
20.【解析】个月中用电量的中位数为千瓦时,
八年级等级的人数为,
超过千瓦时月份的月用电量为,,,,,,,
超过千瓦时月份的月平均用电量为千瓦时,
答:个月中用电量的中位数为以千瓦时,超过千瓦时月份的月平均用电量为千瓦时;
由折线统计图可以看出:、、、、月份的气温低,、月份的气温高,这几个月用电量多,
当气温最高或最低时,用电量最多,
建议是:要节约家庭用电,尽量控制高峰用电答案不唯一,合理即可.
21【解析】在矩形中,,,
四边形是平行四边形,
,
,
为中点,
,
由勾股定理得,
,
,
,,
∽,
,
,
;
猜想,,
在矩形中,,
,
,
,
,
,
,,
∽,
,
,
;
由平行线的性质和对顶角相等,可得∽,∽,
,
令,,
由得:
,,均为等腰三角形,
,,
,
,
.
22.【解析】由图象可知,当时是一次函数,
设将、代入得:
,
解得,
;
在水温下降过程中,设水温与开机时间分的函数关系式为依据题,
把代入解析式得:,
解得,
反比例函数解析式为:,
当时,,
解得:;
由,结合图象,可知每分钟图象重复出现一次,
,,
当时,,
答:饮水机内水温约为.
23.【解析】设与的函数关系式为、为常数,且,
将坐标和分别代入,
得,
解得,
与的函数关系式为.
二次函数可以模拟种产品所获利润的变化趋势.理由如下:
增加,的增加值不是一个常数,
与之间不是一次函数的关系,
一次函数不能模拟种产品所获利润的变化趋势,
不是一个定值,
与之间不是反比例函数的关系,
反比例函数不能模拟种产品所获利润的变化趋势,
二次函数可以模拟种产品所获利润的变化趋势.
将,,,,,分别代入,
得,
解得,
,
当时,,
当时,,
与的函数表达式为.
设对种产品投资万元,则对产品投资万元,
设获得的利润为元,
则,
该二次函数开口向下,对称轴为,,
当时有最大值,,
万元.
答:对产品投资万元、对种产品投资万元能获得最大利润,最大利润为万元.
24.【解析】证明:是的直径,
,
,,
,,
∽,
,
是的半径,且,
是的切线.
解:是的直径,是的弦,且于点,,,
,,
,
,
,
,
,
,
,
的长为.
25.【解析】点,
,
,
,,
把,代入,
得:,
解得:,
抛物线的解析式为:;
过点作,交于点,过点作,交于点,如图所示:
设直线的解析式为,把,代入得:,
解得:,
直线的解析式为:,
同理可得:直线的解析式为:,
,
直线的解析式为:,
联立,
解得:,
点,
,
,,
,
,
,
,
,
,
∽,
,
即,
,
设,则,
,
,
,
当时,有最大值,
,
此时点的坐标为;
作轴,在点下方取,连接,取点关于轴的对称点,连接,如图所示:
则,,
,,
四边形为平行四边形,
,
根据轴对称可知:,
,
两点之间线段最短,
当、、三点在同一直线上时,最小,即最小,
为定值,
此时最小,且最小值为:;
,
抛物线的顶点坐标为,
将抛物线沿着射线方向平移个单位长度得到新抛物线,
,,
将抛物线向右平移个单位,向上平移个单位,正好得出新抛物线,
新抛物线的顶点坐标为,
新抛物线的解析式为:,
根据解析可知:当取得最大值时,,
,
轴,
,
,,
,,
,
作,点在轴正半轴上,过点作于点,如图所示:
则,
设,则,
为等腰直角三角形,
,
,
,
,
,,
,
,
∽,
,即,
解得:,
,
,,,
≌,
,
,
设直线的解析式为:,把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
当与轴的交点正好为关于轴的对称点时,,此时点符合题意,
设直线的解析式为:,
把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
综上分析可知:点的横坐标为或.
26.
【解析】证明,,,
、为等边三角形,
,,,
,即,
≌;
证明:如图,取中点,连接、,
则,,,,
,,,
∽,
,,
,
∽,
,
;
解:,,,
和均为等腰直角三角形,
,
∽,
,
,
则动点在过且平行于的定直线上运动,
延长到,使,连接,
点为线段中点,
,
过点作于,则,即,
过作于,
是等腰直角三角形,,
,,
,
四边形是矩形,
,
,
即线段的最小值为.
故答案为:.
第21页,共21页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.如图,点和点表示的数分别为和,下列式子中正确的是( )
A. B. C. D.
2.下列所给图形是中心对称图形也是轴对称图形的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.年月日,搭载神舟十八号载人飞船的长征二号遥十八运载火箭成功发射为了培养青少年对航天知识学习的兴趣,某校开展航天知识竞赛活动经过几轮筛选,八年级班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛经过统计,四名同学成绩的平均数单位:分及方差如下表所示.
甲 乙 丙 丁
平均数
方差
要选一名成绩好且状态稳定的同学参赛,应选择( )
A. 甲 B. 乙 C. 丙 D. 丁
5.如图,已知直线,将一块含的直角三角板按如图方式放置,其中点,分别落在直线、上若,则等于( )
A. B.
C. D.
6.如图,是的直径,若,则的度数是( )
A. B.
C. D.
7.如图,一次函数与的图象相交于点,则关于的不等式的解集是( )
A.
B.
C.
D.
8.如图,点是正九边形的中心,连接,,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共8小题,每小题3分,共24分。
9.若代数式在实数范围内有意义,则实数的取值范围是 .
10.一种袋装食品标准净重为克,质监部门工作人员为了解该种食品每袋重与标准净重的误差,把食品净重克记为克,那么,食品净重克就记为______克
11.中国传统文化中的“四瑞兽”是古代象征样瑞与方位的神兽,分别为:青龙、白虎、朱雀、玄武小王和小李在美术课上都想从“四瑞兽”中随机选择一个瑞兽进行绘画创作,他们所选瑞兽相同的概率是______.
12.如图,为的切线,点为切点,交于点,点在上,连接、,,若,则的度数为______
13.定义一种法则“”如下:,例如:,若,则的取值范围是______.
14.若关于的方程的一个根是,则另一个根是______.
15.如图,是反比例函数的图象上的一个动点,作点关于原点的对称点,以为斜边作等腰直角三角形,若点的坐标为,则______.
16.某校“综合与实践”活动小组的同学要测量两座楼之间的距离,他们借助无人机设计了如下测量方案:无人机在两楼之间上方的点处,点距地面的高度为,此时观测到楼底部点处的俯角为,楼上点处的俯角为沿水平方向由点飞行到达点,此时测得点处俯角为,其中点,,,,,,均在同一竖直平面内,则楼与之间的距离的长约为______结果精确到参考数据:,,,
三、解答题:本题共10小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
计算:.
18.本小题分
阅读与思考.
阅读下面材料,并完成相应的任务.
求解二元一次方程组,需要通过消元把它转化为一元一次方程来解;求一元二次方程,需要把它转化为两个一元一次方程来解;求解分式方程,需要通过去分母把它转化为整式方程来解各类方程的解法不尽相同,但是它们都用到一种共同的基本数学思想“转化”,即把未知转化为已知来求解用“转化”的数学思想,我们还可以解一些新的方程.
例如,解一元三次方程,通过因式分解把它转化为,通过解方程和,可得原方程的解为,,.
再例如,解根号下含有未知数的方程:,通过两边同时平方转化为,
解得:,,且,不是原方程的解,原方程的解为.
请仔细阅读材料,解下列方程:
解方程:;
解方程:.
19.本小题分
如图,平行四边形中,点在的延长线上,点在的延长线上,满足,连接、连接,分别与,交于点,,且平分.
求证:四边形是菱形;
若,,求四边形的面积.
20.本小题分
如图表示去年某地个月每月平均气温,如图表示该地小聪家去年个月的用电量,如表格表示当地对民用电收费的标准,小聪家常用的电器有灯、冰箱、空调、电车等等.
某地民用电收费标准信息表
月用电量 居民峰谷分时电价
高峰时段电价
::
单位:元 低谷时段电价
::以外
单位:元
千瓦时以下
千瓦时
千瓦时及以上
根据图求出个月中用电量的中位数以及超过千瓦时月份的月平均用电量.
根据统计图与信息表,请描述月用电量与气温间的一些关系,并对家庭用电提出一些建议.
21.本小题分
如图,在矩形中,为上一点,将沿翻折,点落在点处,延长交边于点,过点作分别交,于点,.
当时,若点恰好为的中点,求出,的值.
小明想探究在点运动的过程中,,,之间的数量关系,记,,,在的基础上,他通过几何画板画图,度量,得到以下几组对应值如表格所示,根据数据,请猜想,,三个量的关系以及,之间的数量关系,并说明理由.
如图,过点作分别交,于点,若,,求的值用表示.
22.本小题分
小明家饮水机中原有水的温度为,通电开机后,饮水机自动开始加热此过程中水温与开机时间分满足一次函数关系,当加热到时自动停止加热,随后水温开始下降此过程中水温与开机时间分成反比例关系,当水温降至时,饮水机又自动开始加热,重复上述程序如图所示,根据图中提供的信息,解答下列问题:
求图中的值;
若小明在通电开机后即外出散步,请你预测小明散步分钟回到家时,饮水机内的温度约为多少?
23.本小题分
某企业信息部对,两种产品进行市场调研,数据信息分析如下:
信息:如果单独投资种产品,所获利润万元与投资金额,单位:万元之间存在如图所示的关系;
信息:如果单独投资种产品,则所获利润万元与投资金额万元之间存在如表所示的关系:
万元
万元
求出与的函数关系式;
从所学过的一次函数、二次函数或反比例函数中选择一种适当函数模型,模拟种产品所获利润的变化趋势请说明选择该模型的理由,并求出与的函数表达式;
如果该企业同时对、两种产品共投资万元,请设计一个能获得最大利润的投资方案,并求出按此方案所获得的最大利润.
24.本小题分
如图,在中,直径弦于点,连接,,过点作交于点,过点作交的延长线于点.
求证:是的切线;
若,,求的长.
25.本小题分
如图,在平面直角坐标系中,抛物线与轴交于点,,交轴于点,且.
求该抛物线的函数表达式;
如图,点为直线上方抛物线上的一动点,过点作交于点,,为轴上的动点,在的下方,满足,连接,,当取得最大值时,求点的坐标及的最小值;
将抛物线沿着射线方向平移个单位长度得到新抛物线,在当取得最大值的条件下,点为新抛物线上一点,连接,,当时,请直接写出点的横坐标.
26.本小题分
如图,在与中,,,,点在直线上,连接.
若,求证:≌;
如图,连接,点为线段中点,点为线段中点,连接求证:;
如图,若,,连接,点为线段中点,当点在的延长线上运动时,请直接写出:线段的最小值______.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
8.【答案】
9.【答案】且
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】.
【解析】解:原式
.
18.【解析】,
,
.
或.
,.
,
两边平方,得,
整理,得.
.
,.
且,
不是原方程的解.
原方程的解为.
19.【解析】证明:是平行四边形,
,,
,
,即,
且,即,
四边形是平行四边形,
又且平分,
,,
,
,
平行四边形是菱形;
解:如图,连接交于点,
四边形是菱形,
,
,
,且,
,
,,
,
在中,,,
,
,
,
,
.
20.【解析】个月中用电量的中位数为千瓦时,
八年级等级的人数为,
超过千瓦时月份的月用电量为,,,,,,,
超过千瓦时月份的月平均用电量为千瓦时,
答:个月中用电量的中位数为以千瓦时,超过千瓦时月份的月平均用电量为千瓦时;
由折线统计图可以看出:、、、、月份的气温低,、月份的气温高,这几个月用电量多,
当气温最高或最低时,用电量最多,
建议是:要节约家庭用电,尽量控制高峰用电答案不唯一,合理即可.
21【解析】在矩形中,,,
四边形是平行四边形,
,
,
为中点,
,
由勾股定理得,
,
,
,,
∽,
,
,
;
猜想,,
在矩形中,,
,
,
,
,
,
,,
∽,
,
,
;
由平行线的性质和对顶角相等,可得∽,∽,
,
令,,
由得:
,,均为等腰三角形,
,,
,
,
.
22.【解析】由图象可知,当时是一次函数,
设将、代入得:
,
解得,
;
在水温下降过程中,设水温与开机时间分的函数关系式为依据题,
把代入解析式得:,
解得,
反比例函数解析式为:,
当时,,
解得:;
由,结合图象,可知每分钟图象重复出现一次,
,,
当时,,
答:饮水机内水温约为.
23.【解析】设与的函数关系式为、为常数,且,
将坐标和分别代入,
得,
解得,
与的函数关系式为.
二次函数可以模拟种产品所获利润的变化趋势.理由如下:
增加,的增加值不是一个常数,
与之间不是一次函数的关系,
一次函数不能模拟种产品所获利润的变化趋势,
不是一个定值,
与之间不是反比例函数的关系,
反比例函数不能模拟种产品所获利润的变化趋势,
二次函数可以模拟种产品所获利润的变化趋势.
将,,,,,分别代入,
得,
解得,
,
当时,,
当时,,
与的函数表达式为.
设对种产品投资万元,则对产品投资万元,
设获得的利润为元,
则,
该二次函数开口向下,对称轴为,,
当时有最大值,,
万元.
答:对产品投资万元、对种产品投资万元能获得最大利润,最大利润为万元.
24.【解析】证明:是的直径,
,
,,
,,
∽,
,
是的半径,且,
是的切线.
解:是的直径,是的弦,且于点,,,
,,
,
,
,
,
,
,
,
的长为.
25.【解析】点,
,
,
,,
把,代入,
得:,
解得:,
抛物线的解析式为:;
过点作,交于点,过点作,交于点,如图所示:
设直线的解析式为,把,代入得:,
解得:,
直线的解析式为:,
同理可得:直线的解析式为:,
,
直线的解析式为:,
联立,
解得:,
点,
,
,,
,
,
,
,
,
,
∽,
,
即,
,
设,则,
,
,
,
当时,有最大值,
,
此时点的坐标为;
作轴,在点下方取,连接,取点关于轴的对称点,连接,如图所示:
则,,
,,
四边形为平行四边形,
,
根据轴对称可知:,
,
两点之间线段最短,
当、、三点在同一直线上时,最小,即最小,
为定值,
此时最小,且最小值为:;
,
抛物线的顶点坐标为,
将抛物线沿着射线方向平移个单位长度得到新抛物线,
,,
将抛物线向右平移个单位,向上平移个单位,正好得出新抛物线,
新抛物线的顶点坐标为,
新抛物线的解析式为:,
根据解析可知:当取得最大值时,,
,
轴,
,
,,
,,
,
作,点在轴正半轴上,过点作于点,如图所示:
则,
设,则,
为等腰直角三角形,
,
,
,
,
,,
,
,
∽,
,即,
解得:,
,
,,,
≌,
,
,
设直线的解析式为:,把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
当与轴的交点正好为关于轴的对称点时,,此时点符合题意,
设直线的解析式为:,
把代入得:,
解得:,
直线的解析式为:,
令,
解得:舍去;
综上分析可知:点的横坐标为或.
26.
【解析】证明,,,
、为等边三角形,
,,,
,即,
≌;
证明:如图,取中点,连接、,
则,,,,
,,,
∽,
,,
,
∽,
,
;
解:,,,
和均为等腰直角三角形,
,
∽,
,
,
则动点在过且平行于的定直线上运动,
延长到,使,连接,
点为线段中点,
,
过点作于,则,即,
过作于,
是等腰直角三角形,,
,,
,
四边形是矩形,
,
,
即线段的最小值为.
故答案为:.
第21页,共21页
同课章节目录
