2025年安徽省安庆市中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年安徽省安庆市中考数学模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 158.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 20:37:54 | ||
图片预览




文档简介
2025年安徽省安庆市中考数学模拟试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中,比小的数是( )
A. B. C. D.
2.红河日报年月日报道,玉河铁路是我州连接越南与玉溪的铁路大通道,也是我州连通国内外市场的便捷桥梁玉河铁路自通车以来,已安全发送旅客万人次,将万用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.榫卯是中国传统建筑、家具及其它器械的一种结构方式,被誉为“中华民族千年非遗瑰宝”如图是其中一种卯,其左视图是( )
A. B. C. D.
5.如图,圆的两条直径,是半径上的一点,延长交圆于点,连结交于点已知::,则:为( )
A. :
B. :
C. :
D. :
6.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若,则的度数为( )
A. B. C. D.
7.小明有两根长度分别为和的木棒,他想钉一个三角形的木框现在有根木棒供他选择,其长度分别为、、、小明随手拿了一根,恰好能够组成一个三角形的概率为( )
A. B. C. D.
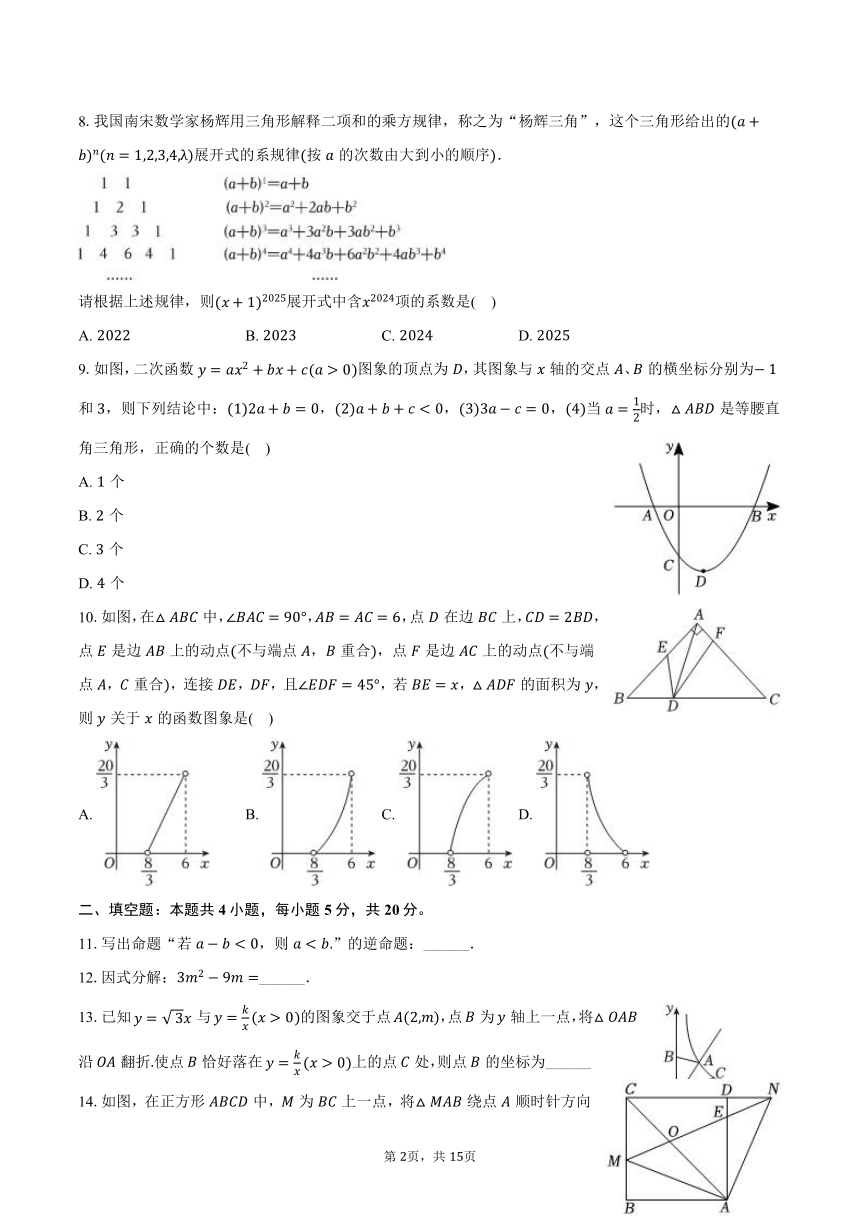
8.我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出的展开式的系规律按的次数由大到小的顺序.
请根据上述规律,则展开式中含项的系数是( )
A. B. C. D.
9.如图,二次函数图象的顶点为,其图象与轴的交点、的横坐标分别为和,则下列结论中:,,,当时,是等腰直角三角形,正确的个数是( )
A. 个
B. 个
C. 个
D. 个
10.如图,在中,,,点在边上,,点是边上的动点不与端点,重合,点是边上的动点不与端点,重合,连接,,且,若,的面积为,则关于的函数图象是( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
11.写出命题“若,则”的逆命题:______.
12.因式分解:______.
13.已知与的图象交于点,点为轴上一点,将沿翻折使点恰好落在上的点处,则点的坐标为______.
14.如图,在正方形中,为上一点,将绕点顺时针方向旋转,得到,连接,交对角线于点,交于点若,,则______;::______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
如图,在平面直角坐标系中,,,,三角形中任意一点经平移后对应点为,将三角形作同样的平移得到三角形.
画出平移后的三角形;
求线段在平移的过程中扫过的面积;
连接,仅用无刻度直尺在线段上画点使.
17.本小题分
“砀山梨”是安徽名特产,果农为了便于销售,将采摘的砀山梨分装为大箱和小箱两种规格,已知个大箱和个小箱能装公斤砀山梨,个大箱和个小箱能装公斤砀山梨求每个大箱和小箱各装多少公斤砀山梨.
18.本小题分
我们约定:关于的代数式,,在,都有意义的的取值范围中,不论取何值,都有为常数,则称代数式,互为“差值代数式”,为“差值”例如:,,因为,所以,互为“差值代数式”,“差值”为根据该约定,解答下列问题.
判断下列各式互为“差值代数式”的是______.
与;与;与.
已知关于的整式,若,互为“差值代数式”,且“差值”为,求的值;
已知关于的整式,,若,互为“差值代数式”,且满足.
求,,的值;
求代数式的最小值.
19.本小题分
如图,在平面直角坐标系中,矩形的顶点,在轴的正半轴上,对角线与交于点,,反比例函数的图象经过点,分别与,交于点,.
若,求的值;
连接,若的面积是,试判断点是否在直线上,并说明理由.
20.本小题分
如图,已知的半径为,四边形内接于,连接、,,.
求的长;
若经过圆心,延长交延长线于点,求的长.
21.本小题分
“华罗庚数学奖”是中国三大顶尖数学奖项之一,是为激励中国数学家在发展中国数学事业中做出突出贡献而设立的小华对截止到第十六届“华罗庚数学奖”得主获奖时的年龄单位:岁数据进行了收集、整理和分析下面是部分信息.
“华罗庚数学奖”得主获奖时的年龄统计图数据分成组:,,,,:
“华罗庚数学奖”得主获奖时的年龄在这一组的是:
“华罗庚数学奖”得主获奖时的年龄数据的平均数、中位数、众数如下:
平均数 中位数 众数
,
根据以上信息,回答下列问题:
截止到第十六届共有______人获得“华罗庚数学奖”;
补全“华罗庚数学奖”得主获奖年龄频数分布直方图;
第十六届“华罗庚数学奖”得主徐宗本院士获奖时的年龄为岁,他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄______填“小”或“大”,理由是______;
22.本小题分
友好图形的定义如下:两个完全重合放置的图形,固定一个顶点,将其中一个图形绕这个顶点旋转,这样的图形称为友好图形,下面我们来探究友好图形旋转的性质.
已知矩形,将矩形绕点旋转到矩形,,.
【尝试发现】
如图,连接,,在旋转过程中,探究 ______;
【类比探究】
如图,在矩形绕点旋转的过程中,使落在矩形对角线上,矩形对角线与相交于点,交于,延长交于点,求的长.
【联系拓广】
将友好矩形中的绕点旋转到的过程中,当构成直角三角形时,求出的长.
23.本小题分
已知抛物线与轴交于、点,顶点为.
求该抛物线的解析式.
如图,点坐标,为抛物线对称轴上一动点,过点的直线平行轴交抛物线于、两点点在点的左侧.
若,求点坐标;
若以为边构造矩形、在线段、上,求该矩形周长的最大值.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】若,则
12.【答案】
13.【答案】
14.【答案】 ;::
15.【解析】解:原式
.
16.【解析】如图,即为所求;
在平移的过程中扫过的面积;
如图,点即为所求;
17.【解析】解:设大箱可装公斤砀山梨,小箱可装公斤砀山梨,
根据题意得:,
解得,
即大箱可装公斤砀山梨,小箱可装公斤砀山梨,
答:大箱可装公斤砀山梨,小箱可装公斤砀山梨.
18.【解析】解::,所以与互为“差值代数式”,“差值”为;
:,所以与不是与;
,所以当时,与互为“差值代数式”,“差值”为;
故答案为:;
关于的整式,,若,互为“差值代数式”,且“差值”为,
,即,
或,
当时,即,
解得或;
当时,即,
解得或;
综上所述,或或或;
关于的整式,,若,互为“差值代数式”,
的结果是常数,
,且“差值”为,
又,
,
,,
答:,,;
,
当的值最小时,原式的值最大,
的最小值为,
的最小值.
19.【解析】矩形的顶点,在轴的正半轴上,对角线与交于点,,,
,,
,
又,
,,,,
对角线与交于点,
点为的中点,
,
反比例函数的图象经过点,
;
点在直线上,理由:
,
,
设,则,,
反比例函数的图象经过点,,
,解得,
,
反比例函数的解析式为,
当时,,
,
点在直线上.
20.【答案】解:,
,
的半径为,
.
,
,
,
,
,,
,
,
平分的外角.
经过圆心,
,即,
,
作,垂足为,
,
为的中位线,
,
.
21.【解析】人,
即截止到第十六届共有人获得“华罗庚数学奖”,
故答案为:;
年龄段的得主获奖人数为:人,
补全频数分布直方图如下:
获奖年龄的中位数为第和名年龄的平均数,
年龄段有人,年龄段有人,
第和名年龄在年龄段,分别为岁和岁,
“华罗庚数学奖”得主获奖年龄的中位数岁,
徐宗本院士获奖时的年龄为岁,
他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄小,理由是徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
故答案为:小,徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
22.【解析】将矩形绕点旋转到矩形,
,,
,
,,
,
∽,
,
故答案为:;
如图,连接,
根据旋转可得,,
,
四边形是矩形,
,,
,
,
,
∽,
,
,
,
,,
,
,
∽,
,即,
解得,经检验是原方程的解,
;
如图,点在上时,,
,,
,
;
如图,点在延长线上时,,
此时,
;
如图,当时,过点作于点,
四边形为矩形,
,,
根据勾股定理可得,
;
如图,当时,过点作交,于点,,
,,
,
,,
∽,
,
,,
在中,,
,,
∽,
,
,
,
,
,
综上所述,的长为或或或.
23.【解析】已知抛物线与轴交于、点,将点,点的坐标分别代入得:
,
解得:,
抛物线的表达式为:;
已知抛物线的顶点为,
,
设,则,
,,
,
,
解得:不合题意,舍去或,
;
为抛物线对称轴上一动点,
设直线的解析式,将点的坐标代入得:
,
解得:,
直线解析式为,
,
,
设矩形周长为,
则,
当时,的最大值为.
第15页,共15页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列各数中,比小的数是( )
A. B. C. D.
2.红河日报年月日报道,玉河铁路是我州连接越南与玉溪的铁路大通道,也是我州连通国内外市场的便捷桥梁玉河铁路自通车以来,已安全发送旅客万人次,将万用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.榫卯是中国传统建筑、家具及其它器械的一种结构方式,被誉为“中华民族千年非遗瑰宝”如图是其中一种卯,其左视图是( )
A. B. C. D.
5.如图,圆的两条直径,是半径上的一点,延长交圆于点,连结交于点已知::,则:为( )
A. :
B. :
C. :
D. :
6.如图,把一块直角三角尺的直角顶点放在直尺的一边上,若,则的度数为( )
A. B. C. D.
7.小明有两根长度分别为和的木棒,他想钉一个三角形的木框现在有根木棒供他选择,其长度分别为、、、小明随手拿了一根,恰好能够组成一个三角形的概率为( )
A. B. C. D.
8.我国南宋数学家杨辉用三角形解释二项和的乘方规律,称之为“杨辉三角”,这个三角形给出的展开式的系规律按的次数由大到小的顺序.
请根据上述规律,则展开式中含项的系数是( )
A. B. C. D.
9.如图,二次函数图象的顶点为,其图象与轴的交点、的横坐标分别为和,则下列结论中:,,,当时,是等腰直角三角形,正确的个数是( )
A. 个
B. 个
C. 个
D. 个
10.如图,在中,,,点在边上,,点是边上的动点不与端点,重合,点是边上的动点不与端点,重合,连接,,且,若,的面积为,则关于的函数图象是( )
A. B. C. D.
二、填空题:本题共4小题,每小题5分,共20分。
11.写出命题“若,则”的逆命题:______.
12.因式分解:______.
13.已知与的图象交于点,点为轴上一点,将沿翻折使点恰好落在上的点处,则点的坐标为______.
14.如图,在正方形中,为上一点,将绕点顺时针方向旋转,得到,连接,交对角线于点,交于点若,,则______;::______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
如图,在平面直角坐标系中,,,,三角形中任意一点经平移后对应点为,将三角形作同样的平移得到三角形.
画出平移后的三角形;
求线段在平移的过程中扫过的面积;
连接,仅用无刻度直尺在线段上画点使.
17.本小题分
“砀山梨”是安徽名特产,果农为了便于销售,将采摘的砀山梨分装为大箱和小箱两种规格,已知个大箱和个小箱能装公斤砀山梨,个大箱和个小箱能装公斤砀山梨求每个大箱和小箱各装多少公斤砀山梨.
18.本小题分
我们约定:关于的代数式,,在,都有意义的的取值范围中,不论取何值,都有为常数,则称代数式,互为“差值代数式”,为“差值”例如:,,因为,所以,互为“差值代数式”,“差值”为根据该约定,解答下列问题.
判断下列各式互为“差值代数式”的是______.
与;与;与.
已知关于的整式,若,互为“差值代数式”,且“差值”为,求的值;
已知关于的整式,,若,互为“差值代数式”,且满足.
求,,的值;
求代数式的最小值.
19.本小题分
如图,在平面直角坐标系中,矩形的顶点,在轴的正半轴上,对角线与交于点,,反比例函数的图象经过点,分别与,交于点,.
若,求的值;
连接,若的面积是,试判断点是否在直线上,并说明理由.
20.本小题分
如图,已知的半径为,四边形内接于,连接、,,.
求的长;
若经过圆心,延长交延长线于点,求的长.
21.本小题分
“华罗庚数学奖”是中国三大顶尖数学奖项之一,是为激励中国数学家在发展中国数学事业中做出突出贡献而设立的小华对截止到第十六届“华罗庚数学奖”得主获奖时的年龄单位:岁数据进行了收集、整理和分析下面是部分信息.
“华罗庚数学奖”得主获奖时的年龄统计图数据分成组:,,,,:
“华罗庚数学奖”得主获奖时的年龄在这一组的是:
“华罗庚数学奖”得主获奖时的年龄数据的平均数、中位数、众数如下:
平均数 中位数 众数
,
根据以上信息,回答下列问题:
截止到第十六届共有______人获得“华罗庚数学奖”;
补全“华罗庚数学奖”得主获奖年龄频数分布直方图;
第十六届“华罗庚数学奖”得主徐宗本院士获奖时的年龄为岁,他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄______填“小”或“大”,理由是______;
22.本小题分
友好图形的定义如下:两个完全重合放置的图形,固定一个顶点,将其中一个图形绕这个顶点旋转,这样的图形称为友好图形,下面我们来探究友好图形旋转的性质.
已知矩形,将矩形绕点旋转到矩形,,.
【尝试发现】
如图,连接,,在旋转过程中,探究 ______;
【类比探究】
如图,在矩形绕点旋转的过程中,使落在矩形对角线上,矩形对角线与相交于点,交于,延长交于点,求的长.
【联系拓广】
将友好矩形中的绕点旋转到的过程中,当构成直角三角形时,求出的长.
23.本小题分
已知抛物线与轴交于、点,顶点为.
求该抛物线的解析式.
如图,点坐标,为抛物线对称轴上一动点,过点的直线平行轴交抛物线于、两点点在点的左侧.
若,求点坐标;
若以为边构造矩形、在线段、上,求该矩形周长的最大值.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】若,则
12.【答案】
13.【答案】
14.【答案】 ;::
15.【解析】解:原式
.
16.【解析】如图,即为所求;
在平移的过程中扫过的面积;
如图,点即为所求;
17.【解析】解:设大箱可装公斤砀山梨,小箱可装公斤砀山梨,
根据题意得:,
解得,
即大箱可装公斤砀山梨,小箱可装公斤砀山梨,
答:大箱可装公斤砀山梨,小箱可装公斤砀山梨.
18.【解析】解::,所以与互为“差值代数式”,“差值”为;
:,所以与不是与;
,所以当时,与互为“差值代数式”,“差值”为;
故答案为:;
关于的整式,,若,互为“差值代数式”,且“差值”为,
,即,
或,
当时,即,
解得或;
当时,即,
解得或;
综上所述,或或或;
关于的整式,,若,互为“差值代数式”,
的结果是常数,
,且“差值”为,
又,
,
,,
答:,,;
,
当的值最小时,原式的值最大,
的最小值为,
的最小值.
19.【解析】矩形的顶点,在轴的正半轴上,对角线与交于点,,,
,,
,
又,
,,,,
对角线与交于点,
点为的中点,
,
反比例函数的图象经过点,
;
点在直线上,理由:
,
,
设,则,,
反比例函数的图象经过点,,
,解得,
,
反比例函数的解析式为,
当时,,
,
点在直线上.
20.【答案】解:,
,
的半径为,
.
,
,
,
,
,,
,
,
平分的外角.
经过圆心,
,即,
,
作,垂足为,
,
为的中位线,
,
.
21.【解析】人,
即截止到第十六届共有人获得“华罗庚数学奖”,
故答案为:;
年龄段的得主获奖人数为:人,
补全频数分布直方图如下:
获奖年龄的中位数为第和名年龄的平均数,
年龄段有人,年龄段有人,
第和名年龄在年龄段,分别为岁和岁,
“华罗庚数学奖”得主获奖年龄的中位数岁,
徐宗本院士获奖时的年龄为岁,
他的获奖年龄比一半以上“华罗庚数学奖”得主获奖年龄小,理由是徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
故答案为:小,徐宗本院士获奖时的年龄小于“华罗庚数学奖”得主获奖年龄的中位数.
22.【解析】将矩形绕点旋转到矩形,
,,
,
,,
,
∽,
,
故答案为:;
如图,连接,
根据旋转可得,,
,
四边形是矩形,
,,
,
,
,
∽,
,
,
,
,,
,
,
∽,
,即,
解得,经检验是原方程的解,
;
如图,点在上时,,
,,
,
;
如图,点在延长线上时,,
此时,
;
如图,当时,过点作于点,
四边形为矩形,
,,
根据勾股定理可得,
;
如图,当时,过点作交,于点,,
,,
,
,,
∽,
,
,,
在中,,
,,
∽,
,
,
,
,
,
综上所述,的长为或或或.
23.【解析】已知抛物线与轴交于、点,将点,点的坐标分别代入得:
,
解得:,
抛物线的表达式为:;
已知抛物线的顶点为,
,
设,则,
,,
,
,
解得:不合题意,舍去或,
;
为抛物线对称轴上一动点,
设直线的解析式,将点的坐标代入得:
,
解得:,
直线解析式为,
,
,
设矩形周长为,
则,
当时,的最大值为.
第15页,共15页
同课章节目录
