2025年浙江省宁波市中考数学适应性试卷(含答案)
文档属性
| 名称 | 2025年浙江省宁波市中考数学适应性试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 160.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 21:13:02 | ||
图片预览



文档简介
2025年浙江省宁波市中考数学适应性试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列个数中最小的是( )
A. B. C. D.
2.由个相同的小正方体组成的立体图形的俯视图如图所示若数字表示其位置上的小正方体的个数,则该立方体的主视图为( )
A. B. C. D.
3.红河日报年月日报道,玉河铁路是我州连接越南与玉溪的铁路大通道,也是我州连通国内外市场的便捷桥梁玉河铁路自通车以来,已安全发送旅客万人次,将万用科学记数法表示为( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.在学校组织的初三学生体检中,某班名同学视力检查数据如表所示:
视力
人数
这名同学视力检查数据的众数、中位数分别是( )
A. , B. , C. , D. ,
6.如图,在舞台设计中,有两个位似的三角形装饰图案和,位似中心为点,经测量它们的相似比是:,那么与的面积之比是( )
A. : B. : C. : D. :
7.若式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
8.如图,已知两条平行线、,点是上的定点,于点,点、分别是、上的动点,且满足,连接交线段于点,于点,则当最大时,的值为( )
A. B. C. D.
9.在平面直角坐标系中,若点,在反比例函数且为常数的图象上,则( )
A. B. C. D.
10.如图所示,菱形有三个顶点,,在上,,点在对角线上,记半径长为,长为,当,的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式:______.
12.若,则______.
13.一个不透明的袋子中装有个红球,个蓝球,个黄球,这些球除颜色外完全相同,从袋子中随机摸出一个球,摸出黄球的概率是 .
14.如图,、是的两条弦,连接、,若的半径为,,则扇形的面积为______结果保留
15.如图,是内一点,,,若、、、分别是、、、的中点,则四边形的周长是
16.如图,等边内接于,为边上一动点不与、重合,连接并延长交边于,将沿翻折为,边交于点,若的周长记为,的周长记为,则的值为 .
三、计算题:本大题共2小题,共12分。
17.计算:.
18.解方程组:.
四、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,是平行四边形的边的中点,连接并延长,交的延长线于点,连结交于点.
求证:.
过点作于点,若是的中点,,求的值.
20.本小题分
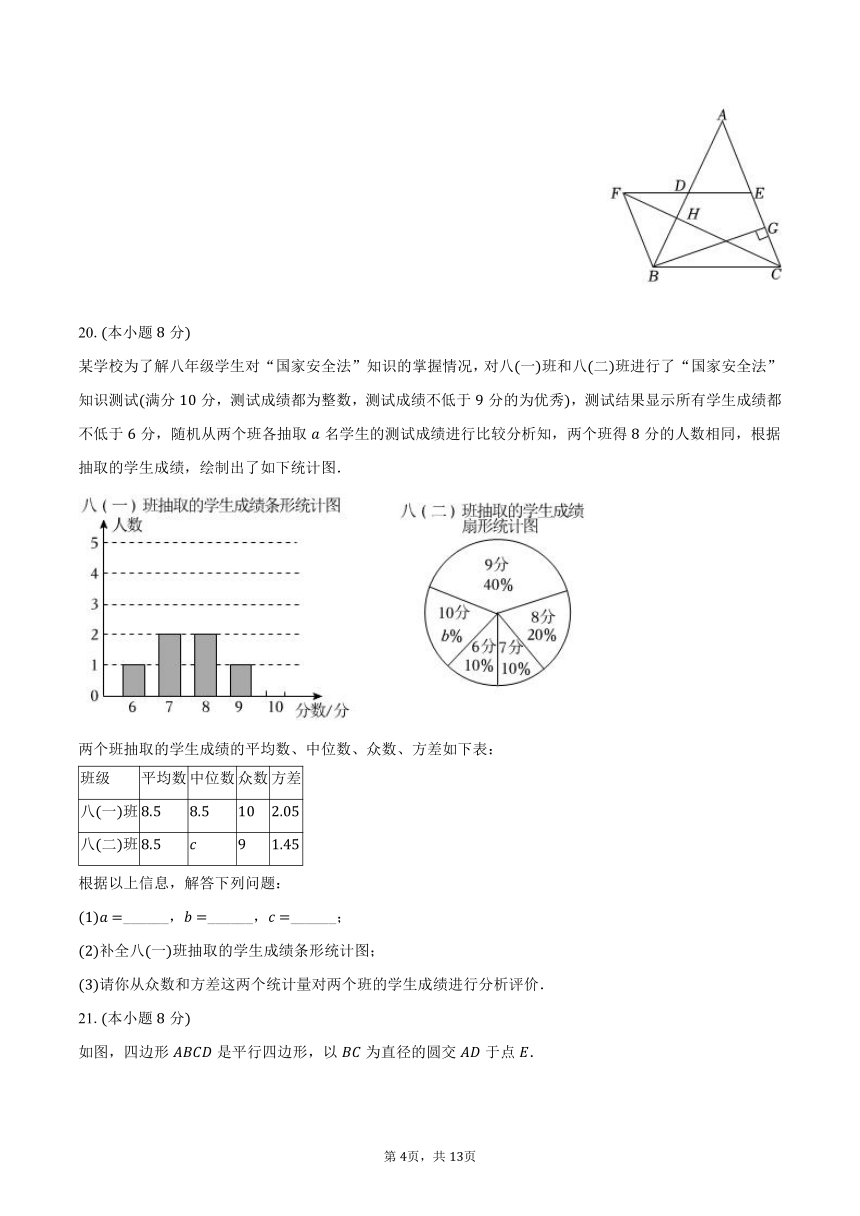
某学校为了解八年级学生对“国家安全法”知识的掌握情况,对八一班和八二班进行了“国家安全法”知识测试满分分,测试成绩都为整数,测试成绩不低于分的为优秀,测试结果显示所有学生成绩都不低于分,随机从两个班各抽取名学生的测试成绩进行比较分析知,两个班得分的人数相同,根据抽取的学生成绩,绘制出了如下统计图.
两个班抽取的学生成绩的平均数、中位数、众数、方差如下表:
班级 平均数 中位数 众数 方差
八一班
八二班
根据以上信息,解答下列问题:
______,______,______;
补全八一班抽取的学生成绩条形统计图;
请你从众数和方差这两个统计量对两个班的学生成绩进行分析评价.
21.本小题分
如图,四边形是平行四边形,以为直径的圆交于点.
请用无刻度的直尺和圆规作出圆心保留作图痕迹,不写作法.
若点是的中点,连接,求证:四边形是平行四边形.
22.本小题分
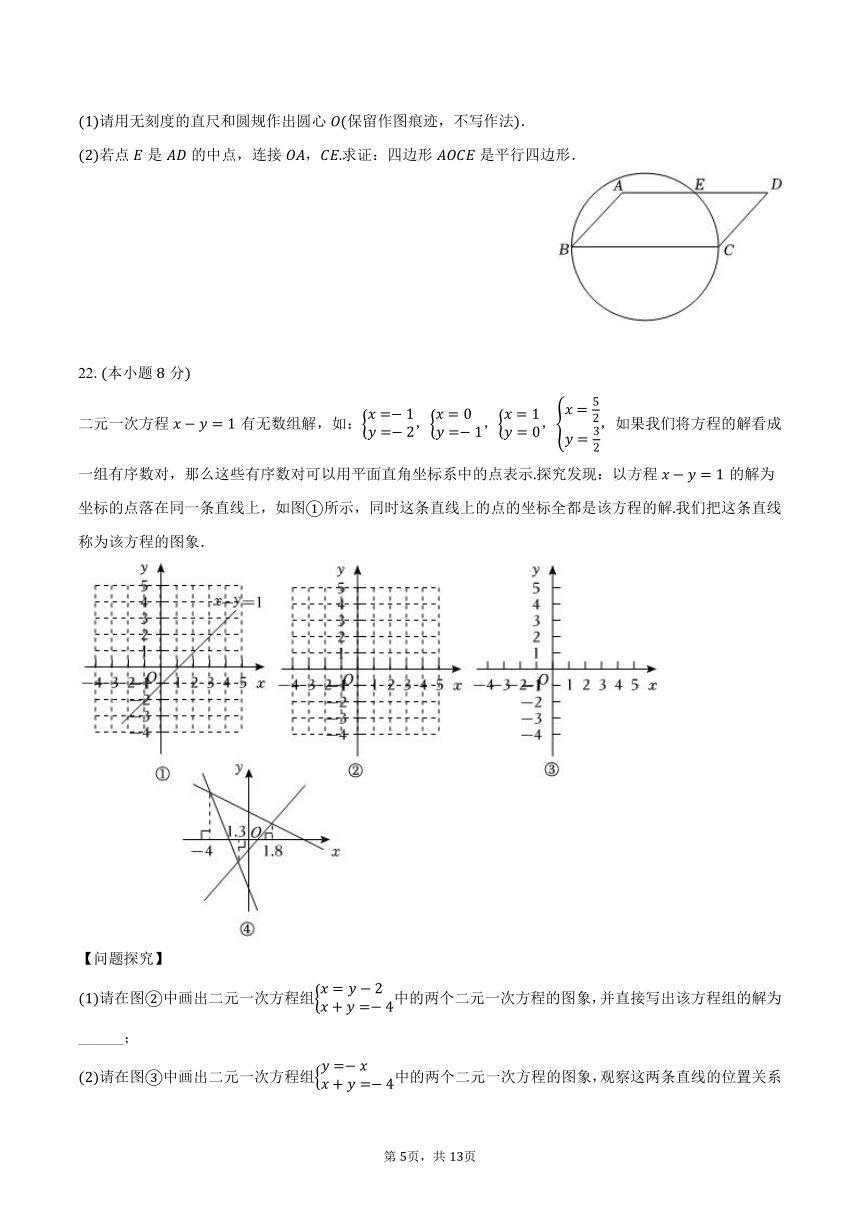
二元一次方程有无数组解,如:,,,,如果我们将方程的解看成一组有序数对,那么这些有序数对可以用平面直角坐标系中的点表示探究发现:以方程的解为坐标的点落在同一条直线上,如图所示,同时这条直线上的点的坐标全都是该方程的解我们把这条直线称为该方程的图象.
【问题探究】
请在图中画出二元一次方程组中的两个二元一次方程的图象,并直接写出该方程组的解为______;
请在图中画出二元一次方程组中的两个二元一次方程的图象,观察这两条直线的位置关系是______,该方程组的解的情况为______;
【拓展应用】
图中画出了个二元一次方程的图象,其中有两个是关于,的二元一次方程组的图象,请直接写出该方程组的解______.
23.本小题分
已知二次函数的顶点坐标为,且其图象经过点直线:与二次函数图象交于点和点在点的左边,与二次函数的对称轴交于点.
求该二次函数的解析式;
若线段被二次函数的对称轴分成的两条线段的长度比为:,求直线的解析式.
24.本小题分
【问题发现】
如图,在中,过点作,垂足为点,且若,则的值为______;
【问题探究】
如图,在中,、的垂直平分线分别交于点、,垂足分别为,,,连接、,求的周长;
【拓展应用】
如图,是一个游乐场的平面示意图,为游乐场大门,其中米,,平分交于点现分别在、上各取一点、,且满足,计划沿、修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米元,求修建这两条轨道总费用的最小值.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:
18.【答案】解:
得:,
解得:,
把代入得:,
解得:,
二元一次方程组的解为:.
19.【解析】证明:是平行四边形的边的中点,
.
四边形是平行四边形,
,,
,,
在与中,
,
≌,
.
.
∽.
:::,
.
解:是的中点,
.
设,则.
,
.
,
,,
.
,
是等腰直角三角形,
,
.
20.【解析】两个班得分的人数相同,
八二班得分的人数为人,
抽取的总人数为:人,即,
,
,
把八二班成绩从小到大排列,第、位的数据为:分、分,
八二班成绩的中位数为:,即.
故答案为:,,;
八一班抽取的学生成绩中得分的有人,分的有人,分的有人,分的有人,
得分的有人,
补全八一班抽取的学生成绩条形统计图如图所示.
从众数上看,两个班抽取的学生成绩中八一班得分的有人,八二班得分的有人,
八一班学生成绩的众数比八二班大;这说明八一班的成绩比八二班好,
八一班抽取的学生成绩的方差为,八二班抽取的学生成绩的方差为,
从方差上看,八一班成绩波动较大,这说明八一班的成绩没有八二班稳定.
21.【解析】解:如图,点即为所求;
证明:四边形都是平行四边形,
,,
是的中点,是的中点,
,
,
四边形是平行四边形.
22.【解析】解:如图.
所以二元一次方程组的解为;
故答案为:;
如图,方程的解为坐标的点组成的直线与方程的解为坐标的点组成的直线平行,
所以方程组无解;
故答案为:平行;无解;
由可得,
在中,当时,,
方程的解组成的直线必过点,
由此可确定方程解组成的直线与方程解组成的直线如下图,
将代入中,得,解得,
关于,的二元一次方程组的解为.
故答案为:.
23.【解析】由题意,二次函数图象顶点为,
可设二次函数为.
又图象过,
.
.
二次函数解析式为,即.
由题意,设,,
点在点的左边,
.
.
.
,且,.
线段被直线分成的两条线段长度比为:,
或.
,或,
当时,
,
.
又,
或.
当时,
,
.
又,
.
或.
综上,当时,直线解析式为;
当时,直线解析式为.
24.【解析】,
,
在和中,
,
≌,
,
故答案为:;
、的垂直平分线分别交于点、,
,,
的周长为;
,,
,
平分,
,
如图:作线段,使,,连接,,
,
,,
,
是等边三角形,
,
,
在和中,
,
≌,
,
,
的最小值为,
米,
两条轨道造价均为每米元,
修建这两条轨道总费用的最小值为元.
答:修建这两条轨道总费用的最小值为元.
第1页,共13页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列个数中最小的是( )
A. B. C. D.
2.由个相同的小正方体组成的立体图形的俯视图如图所示若数字表示其位置上的小正方体的个数,则该立方体的主视图为( )
A. B. C. D.
3.红河日报年月日报道,玉河铁路是我州连接越南与玉溪的铁路大通道,也是我州连通国内外市场的便捷桥梁玉河铁路自通车以来,已安全发送旅客万人次,将万用科学记数法表示为( )
A. B. C. D.
4.下列运算正确的是( )
A. B. C. D.
5.在学校组织的初三学生体检中,某班名同学视力检查数据如表所示:
视力
人数
这名同学视力检查数据的众数、中位数分别是( )
A. , B. , C. , D. ,
6.如图,在舞台设计中,有两个位似的三角形装饰图案和,位似中心为点,经测量它们的相似比是:,那么与的面积之比是( )
A. : B. : C. : D. :
7.若式子在实数范围内有意义,则的取值范围是( )
A. B. C. D.
8.如图,已知两条平行线、,点是上的定点,于点,点、分别是、上的动点,且满足,连接交线段于点,于点,则当最大时,的值为( )
A. B. C. D.
9.在平面直角坐标系中,若点,在反比例函数且为常数的图象上,则( )
A. B. C. D.
10.如图所示,菱形有三个顶点,,在上,,点在对角线上,记半径长为,长为,当,的值发生变化时,下列代数式的值不变的是( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.分解因式:______.
12.若,则______.
13.一个不透明的袋子中装有个红球,个蓝球,个黄球,这些球除颜色外完全相同,从袋子中随机摸出一个球,摸出黄球的概率是 .
14.如图,、是的两条弦,连接、,若的半径为,,则扇形的面积为______结果保留
15.如图,是内一点,,,若、、、分别是、、、的中点,则四边形的周长是
16.如图,等边内接于,为边上一动点不与、重合,连接并延长交边于,将沿翻折为,边交于点,若的周长记为,的周长记为,则的值为 .
三、计算题:本大题共2小题,共12分。
17.计算:.
18.解方程组:.
四、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19.本小题分
如图,是平行四边形的边的中点,连接并延长,交的延长线于点,连结交于点.
求证:.
过点作于点,若是的中点,,求的值.
20.本小题分
某学校为了解八年级学生对“国家安全法”知识的掌握情况,对八一班和八二班进行了“国家安全法”知识测试满分分,测试成绩都为整数,测试成绩不低于分的为优秀,测试结果显示所有学生成绩都不低于分,随机从两个班各抽取名学生的测试成绩进行比较分析知,两个班得分的人数相同,根据抽取的学生成绩,绘制出了如下统计图.
两个班抽取的学生成绩的平均数、中位数、众数、方差如下表:
班级 平均数 中位数 众数 方差
八一班
八二班
根据以上信息,解答下列问题:
______,______,______;
补全八一班抽取的学生成绩条形统计图;
请你从众数和方差这两个统计量对两个班的学生成绩进行分析评价.
21.本小题分
如图,四边形是平行四边形,以为直径的圆交于点.
请用无刻度的直尺和圆规作出圆心保留作图痕迹,不写作法.
若点是的中点,连接,求证:四边形是平行四边形.
22.本小题分
二元一次方程有无数组解,如:,,,,如果我们将方程的解看成一组有序数对,那么这些有序数对可以用平面直角坐标系中的点表示探究发现:以方程的解为坐标的点落在同一条直线上,如图所示,同时这条直线上的点的坐标全都是该方程的解我们把这条直线称为该方程的图象.
【问题探究】
请在图中画出二元一次方程组中的两个二元一次方程的图象,并直接写出该方程组的解为______;
请在图中画出二元一次方程组中的两个二元一次方程的图象,观察这两条直线的位置关系是______,该方程组的解的情况为______;
【拓展应用】
图中画出了个二元一次方程的图象,其中有两个是关于,的二元一次方程组的图象,请直接写出该方程组的解______.
23.本小题分
已知二次函数的顶点坐标为,且其图象经过点直线:与二次函数图象交于点和点在点的左边,与二次函数的对称轴交于点.
求该二次函数的解析式;
若线段被二次函数的对称轴分成的两条线段的长度比为:,求直线的解析式.
24.本小题分
【问题发现】
如图,在中,过点作,垂足为点,且若,则的值为______;
【问题探究】
如图,在中,、的垂直平分线分别交于点、,垂足分别为,,,连接、,求的周长;
【拓展应用】
如图,是一个游乐场的平面示意图,为游乐场大门,其中米,,平分交于点现分别在、上各取一点、,且满足,计划沿、修建两条轨道交通以方便游客游玩,已知两条轨道造价均为每米元,求修建这两条轨道总费用的最小值.
答案和解析
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】
16.【答案】
17.【答案】解:
18.【答案】解:
得:,
解得:,
把代入得:,
解得:,
二元一次方程组的解为:.
19.【解析】证明:是平行四边形的边的中点,
.
四边形是平行四边形,
,,
,,
在与中,
,
≌,
.
.
∽.
:::,
.
解:是的中点,
.
设,则.
,
.
,
,,
.
,
是等腰直角三角形,
,
.
20.【解析】两个班得分的人数相同,
八二班得分的人数为人,
抽取的总人数为:人,即,
,
,
把八二班成绩从小到大排列,第、位的数据为:分、分,
八二班成绩的中位数为:,即.
故答案为:,,;
八一班抽取的学生成绩中得分的有人,分的有人,分的有人,分的有人,
得分的有人,
补全八一班抽取的学生成绩条形统计图如图所示.
从众数上看,两个班抽取的学生成绩中八一班得分的有人,八二班得分的有人,
八一班学生成绩的众数比八二班大;这说明八一班的成绩比八二班好,
八一班抽取的学生成绩的方差为,八二班抽取的学生成绩的方差为,
从方差上看,八一班成绩波动较大,这说明八一班的成绩没有八二班稳定.
21.【解析】解:如图,点即为所求;
证明:四边形都是平行四边形,
,,
是的中点,是的中点,
,
,
四边形是平行四边形.
22.【解析】解:如图.
所以二元一次方程组的解为;
故答案为:;
如图,方程的解为坐标的点组成的直线与方程的解为坐标的点组成的直线平行,
所以方程组无解;
故答案为:平行;无解;
由可得,
在中,当时,,
方程的解组成的直线必过点,
由此可确定方程解组成的直线与方程解组成的直线如下图,
将代入中,得,解得,
关于,的二元一次方程组的解为.
故答案为:.
23.【解析】由题意,二次函数图象顶点为,
可设二次函数为.
又图象过,
.
.
二次函数解析式为,即.
由题意,设,,
点在点的左边,
.
.
.
,且,.
线段被直线分成的两条线段长度比为:,
或.
,或,
当时,
,
.
又,
或.
当时,
,
.
又,
.
或.
综上,当时,直线解析式为;
当时,直线解析式为.
24.【解析】,
,
在和中,
,
≌,
,
故答案为:;
、的垂直平分线分别交于点、,
,,
的周长为;
,,
,
平分,
,
如图:作线段,使,,连接,,
,
,,
,
是等边三角形,
,
,
在和中,
,
≌,
,
,
的最小值为,
米,
两条轨道造价均为每米元,
修建这两条轨道总费用的最小值为元.
答:修建这两条轨道总费用的最小值为元.
第1页,共13页
同课章节目录
