2025年陕西省咸阳市中考数学模拟试卷(含答案)
文档属性
| 名称 | 2025年陕西省咸阳市中考数学模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 212.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 00:00:00 | ||
图片预览




文档简介
2025年陕西省咸阳市中考数学模拟试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的倒数的绝对值是( )
A. B. C. D.
2.由个相同的小正方体组成的立体图形的俯视图如图所示若数字表示其位置上的小正方体的个数,则该立方体的主视图为( )
A. B. C. D.
3.如图,直线,作直线和射线,若平分,,则的度数为( )
A. B. C. D.
4.关于的不等式恰有三个非负整数解,则的取值范围是( )
A. B. C. D.
5.如图,正方形网格中的每一个小正方形的边长都是,设的的长为,估算的运算结果应在( )
A. 到之间
B. 到之间
C. 到之间
D. 到之间
6.已知一次函数为常数,且的图象经过点,点和在该函数图象上,则下列与的关系正确的是( )
A. B. C. D.
7.如图,在中,点是边上一点,连接,将沿翻折,得到,与交于点,连接交于点若,,,的面积为,则的长为( )
A. B. C. D.
8.已知抛物线为常数,且经过点和点,若,则的值可能是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
9.中科院发现“绿色”光刻胶,精度可达,将数据用科学记数法可表示为______.
10.如图,在中,,延长至,过点作的垂线,垂足为,且,则______.
11.如图,点,分别是的外心和内心,连接,,若,则______.
12.已知反比例函数为常数,的图象与直线交于点,则的值为______.
13.如图,在矩形中,,,对角线、交于点,将沿着翻折得到,连接,则______.
三、解答题:本题共13小题,共81分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
计算:.
15.本小题分
化简求值:,其中,.
16.本小题分
解方程.
17.本小题分
如图,在平面直角坐标系中,的三个顶点分别是,,.
将以点为旋转中心逆时针旋转,画出旋转后对应的;
将以点为旋转中心顺时针旋转,画出旋转后对应的;
若将看作由旋转得到的,那么旋转角的度数为______,旋转中心坐标为______.
请直接写出: 的顶点的坐标:______.
18.本小题分
小明同学利用直尺和圆规进行了如下操作:如图,四边形是平行四边形,以点为圆心,任意长为半径画弧,分别交和于点,;分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,分别以点,为圆心,大于的长为半径画弧,两弧相交于,两点,作直线交边于点,连接交于点.
求证:;
若,,求.
19.本小题分
从甲地到乙地,汽车原来需要行驶小时,开通高速公路后,路程比原来缩短了千米,车速平均每小时比原来增加了千米,现在只需要小时即可到达,求甲、乙两地之间高速公路的路程.
20.本小题分
某校对七、八、九年级的学生进行体育综合素质测评,成绩评定为优秀、良好、合格、不合格四个等次为了解这次测试情况,学校从三个年级随机抽取名学生的体育成绩进行统计分析相关数据的统计图表如下:
各年级学生成绩统计表
优秀 良好 合格 不合格
七年级
八年级
九年级
根据以上信息解决下列问题:
在统计表中,的值为______,的值为______;
在扇形统计图中,八年级所对应的扇形圆心角为______;
若该校三个年级共有名学生参加考试,试估计该校学生体育成绩优秀的人数;
若该校已选定优秀代表甲、乙两位同学去参加区里面开展的跳绳、跑步、引体向上、掷实心球四项体育活动比赛,每人任选一项参加,请直接写出甲、乙两位同学刚好选择同一项活动的概率.
21.本小题分
如图是贵阳花果园双子塔,是贵阳国际贸易中心的座和座,是贵州省第一高楼,也是全国已建成的最高双子塔在学会三角函数知识后,家住双子塔附近的小星同学决定用自己学到的知识测量其中一座塔的高度,如图,小星在小区门口点处测得其中一个塔的顶部的仰角为,然后在自家阳台上的点处测得顶部的仰角为,若小星家的阳台到地面的距离为,点到点的水平距离为,且、、三点共线,求的高度结果精确到参考数据:,,
22.本小题分
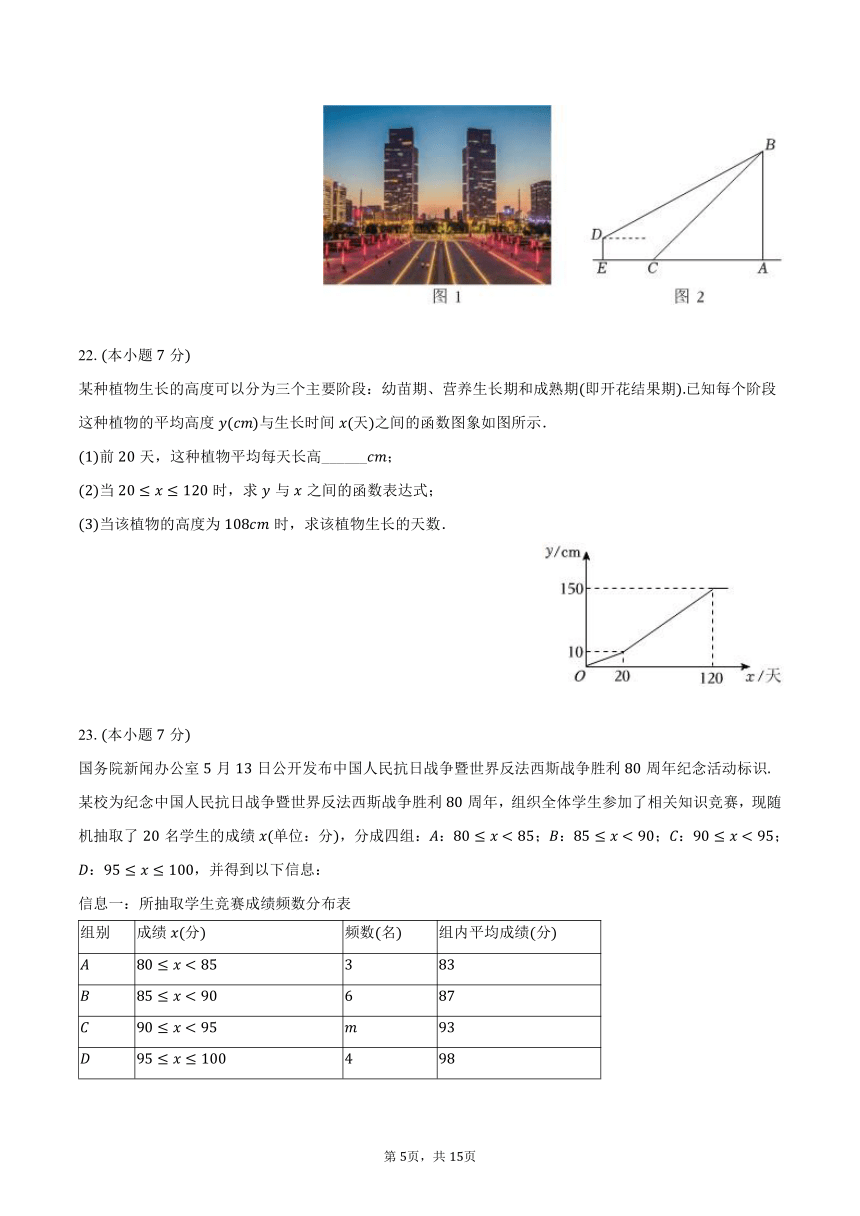
某种植物生长的高度可以分为三个主要阶段:幼苗期、营养生长期和成熟期即开花结果期已知每个阶段这种植物的平均高度与生长时间天之间的函数图象如图所示.
前天,这种植物平均每天长高______;
当时,求与之间的函数表达式;
当该植物的高度为时,求该植物生长的天数.
23.本小题分
国务院新闻办公室月日公开发布中国人民抗日战争暨世界反法西斯战争胜利周年纪念活动标识某校为纪念中国人民抗日战争暨世界反法西斯战争胜利周年,组织全体学生参加了相关知识竞赛,现随机抽取了名学生的成绩单位:分,分成四组::;:;:;:,并得到以下信息:
信息一:所抽取学生竞赛成绩频数分布表
组别 成绩分 频数名 组内平均成绩分
信息二:组的竞赛成绩分别是,,,,,,.
信息三:所抽取学生竞赛成绩的众数在组.
根据以上信息,解答下列问题:
表中______,所抽取学生竞赛成绩的中位数是______分,众数是______分;
求所抽取学生竞赛成绩的平均数;
若该校共有名学生参加此次知识竞赛,成绩在范围内被评为“良好”,请你估计该校参加此次知识竞赛被评为“良好”的学生总人数.
24.本小题分
如图,四边形内接于,是的直径,连接,平分,为延长线上的点,连接,且.
求证:是的切线;
若,,,求的长.
25.本小题分
太阳灶是利用凹面镜会聚光的性质把太阳能收集起来,用于做饭、烧水的一种器具目前应用最广泛的聚光式太阳灶是利用镜面反射会聚阳光,如图,这种太阳灶的镜面设计,可以看成是抛物线绕其对称轴旋转一周所得的旋转抛物面,其原理是若有一束平行光沿对称轴方向射向这个抛物面,则反射光线都会集中反射到一特殊点即抛物线的焦点的位置,于是形成聚光,达到加热的目的用一过抛物线对称轴的平面截抛物面,将所截得的抛物线放在平面直角坐标系中,对称轴与轴重合,顶点与原点重合如图,,已知抛物线的表达式为,则抛物线的焦点为太阳灶采光面为,轴,交轴于.
如图,若太阳灶采光面的直径为米,凹面深度为米,求抛物线的表达式;
如图,已知太阳灶抛物线的焦点坐标为,表示太阳灶边缘最远程反射光同对称轴的夹角,当为时,求此采光面的直径的值.
26.本小题分
【问题探究】
如图,在中,,,、分别是边、的中点,连接,若,则的长为______;
如图,点为等边内一点,连接、,以为一边向的右侧作等边,连接试判断与的数量关系,并说明理由;
【拓展应用】
为落实五育并举,加强劳动教育,某校开展了“五育勤相融,劳动最光荣”劳动教育主题活动,活动设立劳动教育体验基地,供学生进行耕种劳动如图所示的四边形为该基地的示意图,现要在基地一角开辟一个三角形的花圃,点为的中点,并在花圃的一周围一圈栅栏已知,,米,米,求所需栅栏的总长度即的周长.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】.
15.【解析】解:
,
当,时,原式.
16.【解析】解:,
去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为,得,
检验:当时,,
分式方程的解为.
17【解析】如图,即为所求.
如图,即为所求.
分别作线段,,的垂直平分线,相交于点,
则看作由绕点逆时针旋转得到的,
旋转角的度数为,旋转中心坐标为.
故答案为:;.
由图可得, 的顶点的坐标为.
故答案为:.
18.【解析】证明:由条件可知,
又四边形是平行四边形,
,,,
,
,
;
解:设,则,
,
由作图知,垂直平分线段,
,
:::.
由条件可知,,
∽.
,
,
.
19.【解析】设甲、乙两地之间高速公路的路程为千米,则甲、乙两地之间普通公路的路程为千米,
根据题意得:,
解得:.
答:甲、乙两地之间高速公路的路程为千米.
20.【解析】七年级人数为人,
则,
九年级人数为人,
则人,
故答案为:、;
在扇形统计图中,八年级所对应的扇形圆心角为,
故答案为:;
估计该校学生体育成绩优秀的人数为人;
跳绳、跑步、引体向上、掷实心球四项体育活动分别记作、、、,
画树状图如下:
共有种等可能的结果,其甲、乙两位同学刚好选择同一项活动的结果有种结果,
所以甲、乙两位同学刚好选择同一项活动的概率为.
21.【答案】的高度约为.
【解析】解:过点作,垂足为,
由题意得:,,
设,
,
,
在中,,
,
在中,,
,
,
,
解得:,
,
的高度约为.
22.【解析】前天,这种植物平均每天长高.
故答案为:.
当时,这种植物平均每天长高,
则,
当时,与之间的函数表达式为.
当时,得,
解得.
答:当该植物的高度为时,该植物生长的天数为天.
根据平均高度生长天数列式计算即可;
根据这段时间内增加的高度这段时间的天数求出平均每天生长的高度,从而写出与之间的函数表达式即可;
当时,求出对应的值即可.
本题考查一次函数的应用,根据图象进行有关计算是解题的关键.
23.【答案】,,;
分;
名.
【解析】,所抽取学生竞赛成绩的中位数是,众数为,
故答案为:,,;
分,
所抽取学生竞赛成绩的平均数为.
名,
估计该校参加此次知识竞赛被评为“良好”的学生总人数为名.
24.【解析】证明:连接,
四边形内接于,
,
,
,
,
,
平分,
,
,
,
,
是的直径,
,
,
,
,
是的半径,
是的切线;
解:,
设,,
,
,,
∽,
,
,
负值舍去,
.
25.【解析】轴,交轴于,为米,为米,
,
将代入抛物线的表达式为,
得,
,
抛物线的表达式为;
抛物线的焦点坐标为,
,
,
抛物线的表达式为,
,
为等腰直角三角形,
设,
,
,
把代入抛物线表达式,
得,
解得负值舍去,
,,
采光面的直径米.
26.【解析】,,,
,
、分别是边、的中点,
是的中位线,
即,
故答案为:;
理由如下:
,均为等边三角形,
,,,
,
在和中,
,,,
≌,
;
如图,连接,过作交的延长线于点,连接,取中点,连接,
由,,可知,,
,
点为中点,
是的中位线,
,,
,,
,
,
,
,,
,
在和中,
,,,
≌,
,,
,,
是中点,
,,
,,
,
在中,,
,
解得或舍去,
,,
,
的周长米,
故栅栏的总长度为米.
第11页,共15页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.的倒数的绝对值是( )
A. B. C. D.
2.由个相同的小正方体组成的立体图形的俯视图如图所示若数字表示其位置上的小正方体的个数,则该立方体的主视图为( )
A. B. C. D.
3.如图,直线,作直线和射线,若平分,,则的度数为( )
A. B. C. D.
4.关于的不等式恰有三个非负整数解,则的取值范围是( )
A. B. C. D.
5.如图,正方形网格中的每一个小正方形的边长都是,设的的长为,估算的运算结果应在( )
A. 到之间
B. 到之间
C. 到之间
D. 到之间
6.已知一次函数为常数,且的图象经过点,点和在该函数图象上,则下列与的关系正确的是( )
A. B. C. D.
7.如图,在中,点是边上一点,连接,将沿翻折,得到,与交于点,连接交于点若,,,的面积为,则的长为( )
A. B. C. D.
8.已知抛物线为常数,且经过点和点,若,则的值可能是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
9.中科院发现“绿色”光刻胶,精度可达,将数据用科学记数法可表示为______.
10.如图,在中,,延长至,过点作的垂线,垂足为,且,则______.
11.如图,点,分别是的外心和内心,连接,,若,则______.
12.已知反比例函数为常数,的图象与直线交于点,则的值为______.
13.如图,在矩形中,,,对角线、交于点,将沿着翻折得到,连接,则______.
三、解答题:本题共13小题,共81分。解答应写出文字说明,证明过程或演算步骤。
14.本小题分
计算:.
15.本小题分
化简求值:,其中,.
16.本小题分
解方程.
17.本小题分
如图,在平面直角坐标系中,的三个顶点分别是,,.
将以点为旋转中心逆时针旋转,画出旋转后对应的;
将以点为旋转中心顺时针旋转,画出旋转后对应的;
若将看作由旋转得到的,那么旋转角的度数为______,旋转中心坐标为______.
请直接写出: 的顶点的坐标:______.
18.本小题分
小明同学利用直尺和圆规进行了如下操作:如图,四边形是平行四边形,以点为圆心,任意长为半径画弧,分别交和于点,;分别以点,为圆心,大于的长为半径画弧,两弧交于点,作射线交边于点,分别以点,为圆心,大于的长为半径画弧,两弧相交于,两点,作直线交边于点,连接交于点.
求证:;
若,,求.
19.本小题分
从甲地到乙地,汽车原来需要行驶小时,开通高速公路后,路程比原来缩短了千米,车速平均每小时比原来增加了千米,现在只需要小时即可到达,求甲、乙两地之间高速公路的路程.
20.本小题分
某校对七、八、九年级的学生进行体育综合素质测评,成绩评定为优秀、良好、合格、不合格四个等次为了解这次测试情况,学校从三个年级随机抽取名学生的体育成绩进行统计分析相关数据的统计图表如下:
各年级学生成绩统计表
优秀 良好 合格 不合格
七年级
八年级
九年级
根据以上信息解决下列问题:
在统计表中,的值为______,的值为______;
在扇形统计图中,八年级所对应的扇形圆心角为______;
若该校三个年级共有名学生参加考试,试估计该校学生体育成绩优秀的人数;
若该校已选定优秀代表甲、乙两位同学去参加区里面开展的跳绳、跑步、引体向上、掷实心球四项体育活动比赛,每人任选一项参加,请直接写出甲、乙两位同学刚好选择同一项活动的概率.
21.本小题分
如图是贵阳花果园双子塔,是贵阳国际贸易中心的座和座,是贵州省第一高楼,也是全国已建成的最高双子塔在学会三角函数知识后,家住双子塔附近的小星同学决定用自己学到的知识测量其中一座塔的高度,如图,小星在小区门口点处测得其中一个塔的顶部的仰角为,然后在自家阳台上的点处测得顶部的仰角为,若小星家的阳台到地面的距离为,点到点的水平距离为,且、、三点共线,求的高度结果精确到参考数据:,,
22.本小题分
某种植物生长的高度可以分为三个主要阶段:幼苗期、营养生长期和成熟期即开花结果期已知每个阶段这种植物的平均高度与生长时间天之间的函数图象如图所示.
前天,这种植物平均每天长高______;
当时,求与之间的函数表达式;
当该植物的高度为时,求该植物生长的天数.
23.本小题分
国务院新闻办公室月日公开发布中国人民抗日战争暨世界反法西斯战争胜利周年纪念活动标识某校为纪念中国人民抗日战争暨世界反法西斯战争胜利周年,组织全体学生参加了相关知识竞赛,现随机抽取了名学生的成绩单位:分,分成四组::;:;:;:,并得到以下信息:
信息一:所抽取学生竞赛成绩频数分布表
组别 成绩分 频数名 组内平均成绩分
信息二:组的竞赛成绩分别是,,,,,,.
信息三:所抽取学生竞赛成绩的众数在组.
根据以上信息,解答下列问题:
表中______,所抽取学生竞赛成绩的中位数是______分,众数是______分;
求所抽取学生竞赛成绩的平均数;
若该校共有名学生参加此次知识竞赛,成绩在范围内被评为“良好”,请你估计该校参加此次知识竞赛被评为“良好”的学生总人数.
24.本小题分
如图,四边形内接于,是的直径,连接,平分,为延长线上的点,连接,且.
求证:是的切线;
若,,,求的长.
25.本小题分
太阳灶是利用凹面镜会聚光的性质把太阳能收集起来,用于做饭、烧水的一种器具目前应用最广泛的聚光式太阳灶是利用镜面反射会聚阳光,如图,这种太阳灶的镜面设计,可以看成是抛物线绕其对称轴旋转一周所得的旋转抛物面,其原理是若有一束平行光沿对称轴方向射向这个抛物面,则反射光线都会集中反射到一特殊点即抛物线的焦点的位置,于是形成聚光,达到加热的目的用一过抛物线对称轴的平面截抛物面,将所截得的抛物线放在平面直角坐标系中,对称轴与轴重合,顶点与原点重合如图,,已知抛物线的表达式为,则抛物线的焦点为太阳灶采光面为,轴,交轴于.
如图,若太阳灶采光面的直径为米,凹面深度为米,求抛物线的表达式;
如图,已知太阳灶抛物线的焦点坐标为,表示太阳灶边缘最远程反射光同对称轴的夹角,当为时,求此采光面的直径的值.
26.本小题分
【问题探究】
如图,在中,,,、分别是边、的中点,连接,若,则的长为______;
如图,点为等边内一点,连接、,以为一边向的右侧作等边,连接试判断与的数量关系,并说明理由;
【拓展应用】
为落实五育并举,加强劳动教育,某校开展了“五育勤相融,劳动最光荣”劳动教育主题活动,活动设立劳动教育体验基地,供学生进行耕种劳动如图所示的四边形为该基地的示意图,现要在基地一角开辟一个三角形的花圃,点为的中点,并在花圃的一周围一圈栅栏已知,,米,米,求所需栅栏的总长度即的周长.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】.
15.【解析】解:
,
当,时,原式.
16.【解析】解:,
去分母,得,
去括号,得,
移项、合并同类项,得,
系数化为,得,
检验:当时,,
分式方程的解为.
17【解析】如图,即为所求.
如图,即为所求.
分别作线段,,的垂直平分线,相交于点,
则看作由绕点逆时针旋转得到的,
旋转角的度数为,旋转中心坐标为.
故答案为:;.
由图可得, 的顶点的坐标为.
故答案为:.
18.【解析】证明:由条件可知,
又四边形是平行四边形,
,,,
,
,
;
解:设,则,
,
由作图知,垂直平分线段,
,
:::.
由条件可知,,
∽.
,
,
.
19.【解析】设甲、乙两地之间高速公路的路程为千米,则甲、乙两地之间普通公路的路程为千米,
根据题意得:,
解得:.
答:甲、乙两地之间高速公路的路程为千米.
20.【解析】七年级人数为人,
则,
九年级人数为人,
则人,
故答案为:、;
在扇形统计图中,八年级所对应的扇形圆心角为,
故答案为:;
估计该校学生体育成绩优秀的人数为人;
跳绳、跑步、引体向上、掷实心球四项体育活动分别记作、、、,
画树状图如下:
共有种等可能的结果,其甲、乙两位同学刚好选择同一项活动的结果有种结果,
所以甲、乙两位同学刚好选择同一项活动的概率为.
21.【答案】的高度约为.
【解析】解:过点作,垂足为,
由题意得:,,
设,
,
,
在中,,
,
在中,,
,
,
,
解得:,
,
的高度约为.
22.【解析】前天,这种植物平均每天长高.
故答案为:.
当时,这种植物平均每天长高,
则,
当时,与之间的函数表达式为.
当时,得,
解得.
答:当该植物的高度为时,该植物生长的天数为天.
根据平均高度生长天数列式计算即可;
根据这段时间内增加的高度这段时间的天数求出平均每天生长的高度,从而写出与之间的函数表达式即可;
当时,求出对应的值即可.
本题考查一次函数的应用,根据图象进行有关计算是解题的关键.
23.【答案】,,;
分;
名.
【解析】,所抽取学生竞赛成绩的中位数是,众数为,
故答案为:,,;
分,
所抽取学生竞赛成绩的平均数为.
名,
估计该校参加此次知识竞赛被评为“良好”的学生总人数为名.
24.【解析】证明:连接,
四边形内接于,
,
,
,
,
,
平分,
,
,
,
,
是的直径,
,
,
,
,
是的半径,
是的切线;
解:,
设,,
,
,,
∽,
,
,
负值舍去,
.
25.【解析】轴,交轴于,为米,为米,
,
将代入抛物线的表达式为,
得,
,
抛物线的表达式为;
抛物线的焦点坐标为,
,
,
抛物线的表达式为,
,
为等腰直角三角形,
设,
,
,
把代入抛物线表达式,
得,
解得负值舍去,
,,
采光面的直径米.
26.【解析】,,,
,
、分别是边、的中点,
是的中位线,
即,
故答案为:;
理由如下:
,均为等边三角形,
,,,
,
在和中,
,,,
≌,
;
如图,连接,过作交的延长线于点,连接,取中点,连接,
由,,可知,,
,
点为中点,
是的中位线,
,,
,,
,
,
,
,,
,
在和中,
,,,
≌,
,,
,,
是中点,
,,
,,
,
在中,,
,
解得或舍去,
,,
,
的周长米,
故栅栏的总长度为米.
第11页,共15页
同课章节目录
