2025年安徽省滁州市中考数学冲刺试卷(含答案)
文档属性
| 名称 | 2025年安徽省滁州市中考数学冲刺试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 172.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 21:59:27 | ||
图片预览




文档简介
2025年安徽省滁州市中考数学冲刺试卷
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )
A. B.
C. 纳米 D. 微云人工智能
2.年,模型发布,爆火全球,据数据统计,截止到年月日,该应用的下载量超过亿次,周活跃用户达到了万其中数据“万”用科学记数法可表示为( )
A. B. C. D.
3.下列计算中,正确的是( )
A. B. C. D.
4.如图是由两个完全一样的正方体和一个长方体组成的几何体,其主视图是( )
A.
B.
C.
D.
5.北京大兴国际机场于年月日正式投入运营.小贝和小京分别从地和地出发赶往机场乘坐飞机,出行方式、路径及路程如下表所示:
出行方式 路径 路程
地铁 地大兴机场 全程约公里
公交 地大兴机场 全程约公里
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小贝比小京少用了半小时到达机场.若设公交的平均速度为公里时,根据题意可列方程( )
A. B. C. D.
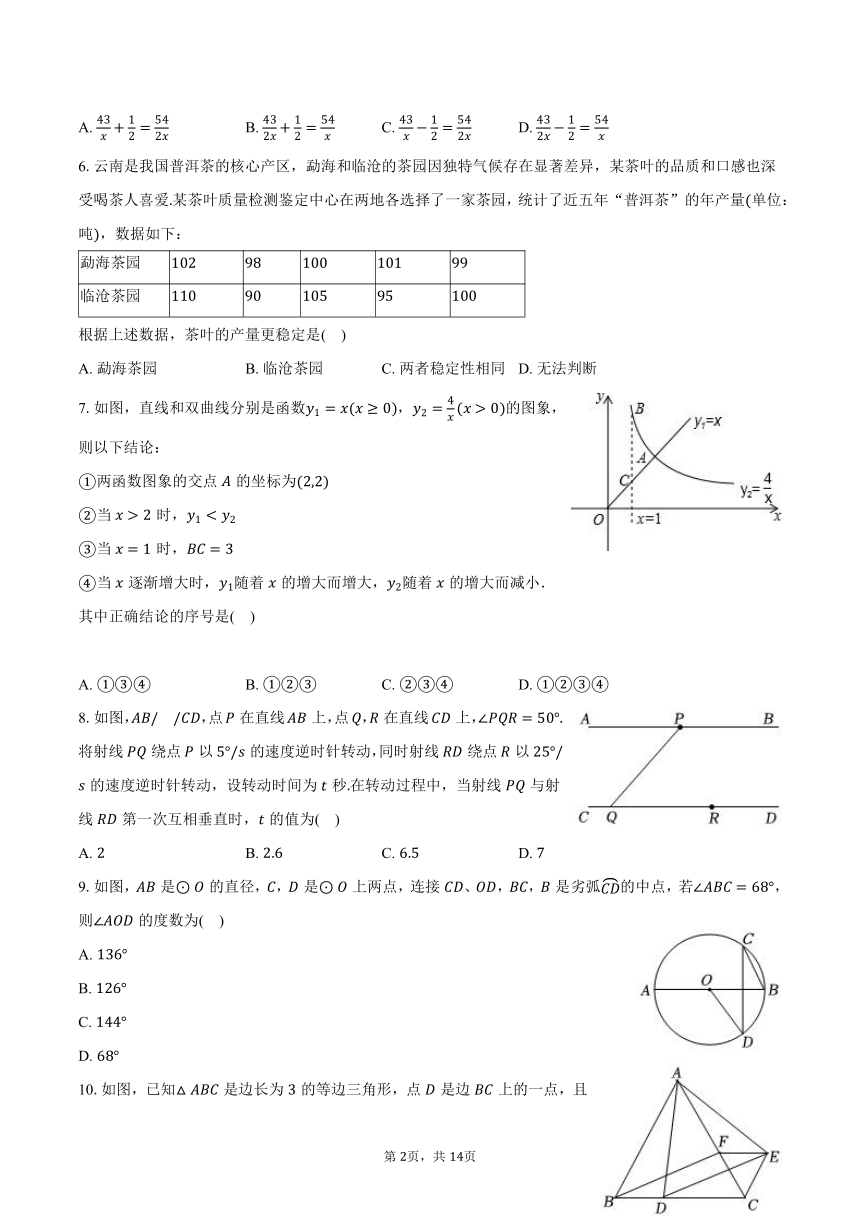
6.云南是我国普洱茶的核心产区,勐海和临沧的茶园因独特气候存在显著差异,某茶叶的品质和口感也深受喝茶人喜爱某茶叶质量检测鉴定中心在两地各选择了一家茶园,统计了近五年“普洱茶”的年产量单位:吨,数据如下:
勐海茶园
临沧茶园
根据上述数据,茶叶的产量更稳定是( )
A. 勐海茶园 B. 临沧茶园 C. 两者稳定性相同 D. 无法判断
7.如图,直线和双曲线分别是函数,的图象,则以下结论:
两函数图象的交点的坐标为
当时,
当时,
当逐渐增大时,随着的增大而增大,随着的增大而减小.
其中正确结论的序号是( )
A. B. C. D.
8.如图,,点在直线上,点,在直线上,将射线绕点以的速度逆时针转动,同时射线绕点以的速度逆时针转动,设转动时间为秒在转动过程中,当射线与射线第一次互相垂直时,的值为( )
A. B. C. D.
9.如图,是的直径,,是上两点,连接、,,是劣弧的中点,若,则的度数为( )
A.
B.
C.
D.
10.如图,已知是边长为的等边三角形,点是边上的一点,且,以为边作等边,过点作,交于点,连接,则四边形的面积是( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分。
11.分解因式:______.
12.如图,在平面直角坐标系中,一次函数的图象分别与、轴交于点、,点是线段的中点,连接,作于点交轴于点,则线段 ______.
13.如图,正方形内接于,点为弧上的动点不与墙点重合,连接,过点作于点,连接,若的半径为,则长的最小值为______.
14.若对恒成立,则方程的两根之积为______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
如图,在边长为单位的正方形网格中有,点,,都在格点上.
求的面积;
在图中画出关于直线对称的;
在直线上画出点,使得最小.
17.本小题分
【阅读材料】对于任意实数,都有.
当分别取值,,,,,时,得到下列有一定规律的等式:
第个等式;
第个等式;
第个等式;
第个等式;
第个等式;
把以上个等式相加,并整理、化简,
得,
进一步化简,得.
【初步理解】有一列数,,,,满足以下等式:
,,,,,
根据阅读材料、以上等式所包含的规律,解决问题:
______;
______;______;用含的代数式表示
【深化应用】
结合阅读材料、等式,求的值.
18.本小题分
某厂生产一种零件,每个成本为元,销售单价为元.该厂为鼓励客户购买这种零件,决定当一次购买零件数超过个时,每多购买一个,全部零件的销售单价均降低元,但不能低于元.
当一次购买多少个零件时,销售单价恰为元?
当客户一次购买个零件时,该厂获得的利润是多少?
当客户一次购买个零件时,该厂获得的利润是多少?利润售价成本
19.本小题分
仙游寺法王塔是陕西省第四批全国重点文物保护单位之一天气晴朗的周末,某数学兴趣小组的同学在综合实践活动中利用学过的数学知识测量法王塔的高度.
【测量过程】如图,该小组成员小明在处放置一个与地面垂直的标杆,同一时刻标杆的影子顶端与法王塔的影子顶端重合于地面上的点处,小组成员小亮在处利用测角仪测出法王塔塔顶的仰角.
【测量数据】,,,.
【参考数据】,,.
已知,,,点、、、在同一条水平直线上,图中所有点均在同一平面内请你根据以上信息求出法王塔的高度.
20.本小题分
如图,在中,,以为直径作半圆,交于点,连接过点作,垂足为点.
求证:是的切线;
求证:.
21.本小题分
国务院新闻办公室月日公开发布中国人民抗日战争暨世界反法西斯战争胜利周年纪念活动标识某校为纪念中国人民抗日战争暨世界反法西斯战争胜利周年,组织全体学生参加了相关知识竞赛,现随机抽取了名学生的成绩单位:分,分成四组::;:;:;:,并得到以下信息:
信息一:所抽取学生竞赛成绩频数分布表
组别 成绩分 频数名 组内平均成绩分
信息二:组的竞赛成绩分别是,,,,,,.
信息三:所抽取学生竞赛成绩的众数在组.
根据以上信息,解答下列问题:
表中______,所抽取学生竞赛成绩的中位数是______分,众数是______分;
求所抽取学生竞赛成绩的平均数;
若该校共有名学生参加此次知识竞赛,成绩在范围内被评为“良好”,请你估计该校参加此次知识竞赛被评为“良好”的学生总人数.
22.本小题分
综合与实践
如图,投掷铅球时,铅球的飞行路径可以近似看作一条抛物线抛掷铅球时,运动员出球的速度、角度、高度以及空气阻力等是影响抛掷距离的主要因素小明在学校体育场借助红外线检测仪检测三种不同的投掷抛物线,,已知三次抛掷铅球时,出手速度相同,出球角度分别为,,,通过投掷测试,小明希望得到最适合自己的投掷角度.
出球角度 抛物线 相关数据 相关结论
铅球与出球位置的水平距离 的长 运动轨迹的函数解析式
铅球与地面的竖直距离
铅球与地面的竖直距离
铅球与地面的竖直距离
【基础应用】
图中点的坐标为______,的值为______;
【应用与说理】
请判断在,,三个出球角度中,小明以哪一个角度投掷铅球的水平距离最大,并说明理由.
【拓展学习】
根据中的判断结果,小明画出了最大时对应的抛物线,如图已知该抛物线交轴于点,是一个斜坡面,点是抛物线上且在线段上方的一个动点,轴于点,交于点,为点到的铅垂距离,求出的最大值.
23.本小题分
已知是的直径,是上的一点,的平分线交于点,是延长线上一点,满足.
如图,求证:与相切;
试判断与,哪个式子成立?并说明理由.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:
.
16.【解析】.
如图:即为所求作;
如图,连接,交直线于点,连接,
此时,为最小值,
点即为所求.
17.【解析】有一列数,,,,满足以下等式:
,,,,,
,
故答案为:;
由归纳可得:;
,,,,,,
把所有的等式相加可得:
;
故答案为:;;
,
,
,
,
,
,
,
整理得:,
,
18.【答案】解:当一次购买个零件时,销售单价恰为元,
依题意得:
解之得:;
,
,
当客户一次购买个零件时,该厂获得的利润是:元
当客户一次购买个零件时,该厂获得的利润是:元
19.【解析】解:延长交于点,
由题意得:,四边形是矩形,
,,
在中,,
,
,
,,
,
,
∽,
,
即,
,
,
解得:,
,
法王塔的高度为.
20.【答案】证明:连接,如图,
为的直径,
,
,
,
平分,即,
,
为的中位线,
,
,
,
是的切线;
证明:,,
∽,
,
,
,
.
21.【解析】,所抽取学生竞赛成绩的中位数是,众数为,
故答案为:,,;
分,
所抽取学生竞赛成绩的平均数为.
名,
估计该校参加此次知识竞赛被评为“良好”的学生总人数为名.
22.【解析】解:把代入得,把代入得,,
,,
故答案为:,;
出球角度为时,把代入,
得,
解得舍.
出球角度为时,把代入,
得,
解得,舍.
由表可知,出球角度为时,抛物线对应的长为,
.
小明投掷铅球出球角度为时,抛掷铅球的水平距离最大.
设直线的解析式为,设点的横坐标为.
,
将代入得,
解得,
直线的函数解析式为,
,
.
,
当时,取得最大值,最大值为.
23.【解析】证明:连接,
是直径,
,
,
,
,
.
,
,
∽,
,
,
即,
,
为半径,
与相切;
解:,理由如下:
平分,
,
,
,
,,
,
,
,
,
,
,
.
第1页,共13页
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )
A. B.
C. 纳米 D. 微云人工智能
2.年,模型发布,爆火全球,据数据统计,截止到年月日,该应用的下载量超过亿次,周活跃用户达到了万其中数据“万”用科学记数法可表示为( )
A. B. C. D.
3.下列计算中,正确的是( )
A. B. C. D.
4.如图是由两个完全一样的正方体和一个长方体组成的几何体,其主视图是( )
A.
B.
C.
D.
5.北京大兴国际机场于年月日正式投入运营.小贝和小京分别从地和地出发赶往机场乘坐飞机,出行方式、路径及路程如下表所示:
出行方式 路径 路程
地铁 地大兴机场 全程约公里
公交 地大兴机场 全程约公里
由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小贝比小京少用了半小时到达机场.若设公交的平均速度为公里时,根据题意可列方程( )
A. B. C. D.
6.云南是我国普洱茶的核心产区,勐海和临沧的茶园因独特气候存在显著差异,某茶叶的品质和口感也深受喝茶人喜爱某茶叶质量检测鉴定中心在两地各选择了一家茶园,统计了近五年“普洱茶”的年产量单位:吨,数据如下:
勐海茶园
临沧茶园
根据上述数据,茶叶的产量更稳定是( )
A. 勐海茶园 B. 临沧茶园 C. 两者稳定性相同 D. 无法判断
7.如图,直线和双曲线分别是函数,的图象,则以下结论:
两函数图象的交点的坐标为
当时,
当时,
当逐渐增大时,随着的增大而增大,随着的增大而减小.
其中正确结论的序号是( )
A. B. C. D.
8.如图,,点在直线上,点,在直线上,将射线绕点以的速度逆时针转动,同时射线绕点以的速度逆时针转动,设转动时间为秒在转动过程中,当射线与射线第一次互相垂直时,的值为( )
A. B. C. D.
9.如图,是的直径,,是上两点,连接、,,是劣弧的中点,若,则的度数为( )
A.
B.
C.
D.
10.如图,已知是边长为的等边三角形,点是边上的一点,且,以为边作等边,过点作,交于点,连接,则四边形的面积是( )
A.
B.
C.
D.
二、填空题:本题共4小题,每小题5分,共20分。
11.分解因式:______.
12.如图,在平面直角坐标系中,一次函数的图象分别与、轴交于点、,点是线段的中点,连接,作于点交轴于点,则线段 ______.
13.如图,正方形内接于,点为弧上的动点不与墙点重合,连接,过点作于点,连接,若的半径为,则长的最小值为______.
14.若对恒成立,则方程的两根之积为______.
三、解答题:本题共9小题,共90分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:.
16.本小题分
如图,在边长为单位的正方形网格中有,点,,都在格点上.
求的面积;
在图中画出关于直线对称的;
在直线上画出点,使得最小.
17.本小题分
【阅读材料】对于任意实数,都有.
当分别取值,,,,,时,得到下列有一定规律的等式:
第个等式;
第个等式;
第个等式;
第个等式;
第个等式;
把以上个等式相加,并整理、化简,
得,
进一步化简,得.
【初步理解】有一列数,,,,满足以下等式:
,,,,,
根据阅读材料、以上等式所包含的规律,解决问题:
______;
______;______;用含的代数式表示
【深化应用】
结合阅读材料、等式,求的值.
18.本小题分
某厂生产一种零件,每个成本为元,销售单价为元.该厂为鼓励客户购买这种零件,决定当一次购买零件数超过个时,每多购买一个,全部零件的销售单价均降低元,但不能低于元.
当一次购买多少个零件时,销售单价恰为元?
当客户一次购买个零件时,该厂获得的利润是多少?
当客户一次购买个零件时,该厂获得的利润是多少?利润售价成本
19.本小题分
仙游寺法王塔是陕西省第四批全国重点文物保护单位之一天气晴朗的周末,某数学兴趣小组的同学在综合实践活动中利用学过的数学知识测量法王塔的高度.
【测量过程】如图,该小组成员小明在处放置一个与地面垂直的标杆,同一时刻标杆的影子顶端与法王塔的影子顶端重合于地面上的点处,小组成员小亮在处利用测角仪测出法王塔塔顶的仰角.
【测量数据】,,,.
【参考数据】,,.
已知,,,点、、、在同一条水平直线上,图中所有点均在同一平面内请你根据以上信息求出法王塔的高度.
20.本小题分
如图,在中,,以为直径作半圆,交于点,连接过点作,垂足为点.
求证:是的切线;
求证:.
21.本小题分
国务院新闻办公室月日公开发布中国人民抗日战争暨世界反法西斯战争胜利周年纪念活动标识某校为纪念中国人民抗日战争暨世界反法西斯战争胜利周年,组织全体学生参加了相关知识竞赛,现随机抽取了名学生的成绩单位:分,分成四组::;:;:;:,并得到以下信息:
信息一:所抽取学生竞赛成绩频数分布表
组别 成绩分 频数名 组内平均成绩分
信息二:组的竞赛成绩分别是,,,,,,.
信息三:所抽取学生竞赛成绩的众数在组.
根据以上信息,解答下列问题:
表中______,所抽取学生竞赛成绩的中位数是______分,众数是______分;
求所抽取学生竞赛成绩的平均数;
若该校共有名学生参加此次知识竞赛,成绩在范围内被评为“良好”,请你估计该校参加此次知识竞赛被评为“良好”的学生总人数.
22.本小题分
综合与实践
如图,投掷铅球时,铅球的飞行路径可以近似看作一条抛物线抛掷铅球时,运动员出球的速度、角度、高度以及空气阻力等是影响抛掷距离的主要因素小明在学校体育场借助红外线检测仪检测三种不同的投掷抛物线,,已知三次抛掷铅球时,出手速度相同,出球角度分别为,,,通过投掷测试,小明希望得到最适合自己的投掷角度.
出球角度 抛物线 相关数据 相关结论
铅球与出球位置的水平距离 的长 运动轨迹的函数解析式
铅球与地面的竖直距离
铅球与地面的竖直距离
铅球与地面的竖直距离
【基础应用】
图中点的坐标为______,的值为______;
【应用与说理】
请判断在,,三个出球角度中,小明以哪一个角度投掷铅球的水平距离最大,并说明理由.
【拓展学习】
根据中的判断结果,小明画出了最大时对应的抛物线,如图已知该抛物线交轴于点,是一个斜坡面,点是抛物线上且在线段上方的一个动点,轴于点,交于点,为点到的铅垂距离,求出的最大值.
23.本小题分
已知是的直径,是上的一点,的平分线交于点,是延长线上一点,满足.
如图,求证:与相切;
试判断与,哪个式子成立?并说明理由.
答案
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
13.【答案】
14.【答案】
15.【答案】解:
.
16.【解析】.
如图:即为所求作;
如图,连接,交直线于点,连接,
此时,为最小值,
点即为所求.
17.【解析】有一列数,,,,满足以下等式:
,,,,,
,
故答案为:;
由归纳可得:;
,,,,,,
把所有的等式相加可得:
;
故答案为:;;
,
,
,
,
,
,
,
整理得:,
,
18.【答案】解:当一次购买个零件时,销售单价恰为元,
依题意得:
解之得:;
,
,
当客户一次购买个零件时,该厂获得的利润是:元
当客户一次购买个零件时,该厂获得的利润是:元
19.【解析】解:延长交于点,
由题意得:,四边形是矩形,
,,
在中,,
,
,
,,
,
,
∽,
,
即,
,
,
解得:,
,
法王塔的高度为.
20.【答案】证明:连接,如图,
为的直径,
,
,
,
平分,即,
,
为的中位线,
,
,
,
是的切线;
证明:,,
∽,
,
,
,
.
21.【解析】,所抽取学生竞赛成绩的中位数是,众数为,
故答案为:,,;
分,
所抽取学生竞赛成绩的平均数为.
名,
估计该校参加此次知识竞赛被评为“良好”的学生总人数为名.
22.【解析】解:把代入得,把代入得,,
,,
故答案为:,;
出球角度为时,把代入,
得,
解得舍.
出球角度为时,把代入,
得,
解得,舍.
由表可知,出球角度为时,抛物线对应的长为,
.
小明投掷铅球出球角度为时,抛掷铅球的水平距离最大.
设直线的解析式为,设点的横坐标为.
,
将代入得,
解得,
直线的函数解析式为,
,
.
,
当时,取得最大值,最大值为.
23.【解析】证明:连接,
是直径,
,
,
,
,
.
,
,
∽,
,
,
即,
,
为半径,
与相切;
解:,理由如下:
平分,
,
,
,
,,
,
,
,
,
,
,
.
第1页,共13页
同课章节目录
