【暑假专项培优】专题11 和差问题—小升初奥数思维之典型应用题精讲精练讲义(通用版)
文档属性
| 名称 | 【暑假专项培优】专题11 和差问题—小升初奥数思维之典型应用题精讲精练讲义(通用版) |  | |
| 格式 | docx | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 11:35:15 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
小升初奥数思维之典型应用题精讲精练讲义(通用版)
专题11 和差问题
【第一部分:知识归纳】
一、基本概念
1、和差问题是指已知两个数的和与差,求这两个数的数学问题。这是小学阶段最基础的应用题类型之一,也是解决更复杂问题的重要基础。
2、核心公式:
较大数 = (和 + 差) ÷ 2
较小数 = (和 - 差) ÷ 2
二、解题四步法
步骤1:判断题型
确认题目中是否明确给出或隐含两个数的和与差
步骤2:画线段图
较大数:|___________|___|
较小数:|___________|
(差的部分用不同颜色标出)
步骤3:选择公式
根据所求的是较大数还是较小数选择对应公式
步骤4:计算验证
将结果代入原题验证是否符合和差关系
三、五大经典题型
题型1:基础型
例题:甲乙两数之和为58,差为12,求这两个数。
解答:较大数 = (58 + 12) ÷ 2 = 35
较小数 = (58 - 12) ÷ 2 = 23
题型2:隐含差型
例题:
哥哥和妹妹共有48元,哥哥给妹妹6元后两人钱数相等。原来各有多少钱?
解答:差 = 6 × 2 = 12元(给6元相当于差减少12元)
哥哥原有 = (48 + 12) ÷ 2 = 30元
妹妹原有 = 48 - 30 = 18元
题型3:多对象型
例题:
甲乙丙三数之和为120,甲比乙大10,乙比丙大8,求这三个数。
解答:设丙为x,则乙=x+8,甲=x+18
x+(x+8)+(x+18)=120 → x=94/3≈31.33
∴ 丙≈31.33,乙≈39.33,甲≈49.33
题型4:年龄问题
例题:
父子年龄和是50岁,5年后父亲比儿子大24岁。现在两人各多少岁?
解答:年龄差不变:24岁
父亲现在 = (50 + 24) ÷ 2 = 37岁
儿子现在 = 50 - 37 = 13岁
题型5:图形应用
例题:
长方形周长40cm,长比宽多4cm,求面积。
解答:长+宽=40÷2=20cm
长=(20+4)÷2=12cm
宽=20-12=8cm
面积=12×8=96cm
四、易错点与技巧
1、常见错误
忽略隐含差:如"给多少后相等"类问题
单位不统一:和与差的单位不一致
年龄差不变:忘记年龄差是固定值
公式记反:混淆较大数和较小数的公式
2、解题技巧
画图法:用线段图直观展示数量关系
举例法:用具体数字验证思路
方程法:设未知数建立简单方程
验证法:计算后检查是否满足原条件
【第二部分:能力提升】
1.一个真分数的分子和分母的和是29,分母与分子的差是7,这个真分数是多少?
2.小明和小红共收集邮票84张,小明收集的邮票比小红多14张,小明和小红各收集多少张邮票?
3.哥哥6年前的岁数等于弟弟8年后的岁数.哥哥5年后与弟弟3年前的年龄和是38岁.求兄弟二人今年各几岁
4.某市红领巾小学图书室里有个书架有两层,共有图书270本,如果从第一层书架上拿38本给第二层书架,则两层书架上的书就相等。求原来两层书架上的书各有多少本?
5.张宁和王星一共有画片86张。王星比张宁多16张。两人各有画片多少张?(先把已知条件在线段图上表示出来,再解答)
6.一个长方形菜园周长是72米,宽比长少4米。这个菜园的面积是多少平方米?
7.有一种小虫,每隔2秒钟分裂一次。分裂后的2只新的小虫经过2秒钟后又会分裂。如果最初瓶中只有1只小虫,那么2秒后变2只,再过2秒后就变4只……2分钟后,正好满满一瓶小虫。现在这个瓶内最初放入2只这样的小虫。经过多长时间,正巧也是满满一瓶小虫?
8.甲、乙两人的年龄之和为27岁,甲比乙大3岁,那么甲、乙两人各多大?
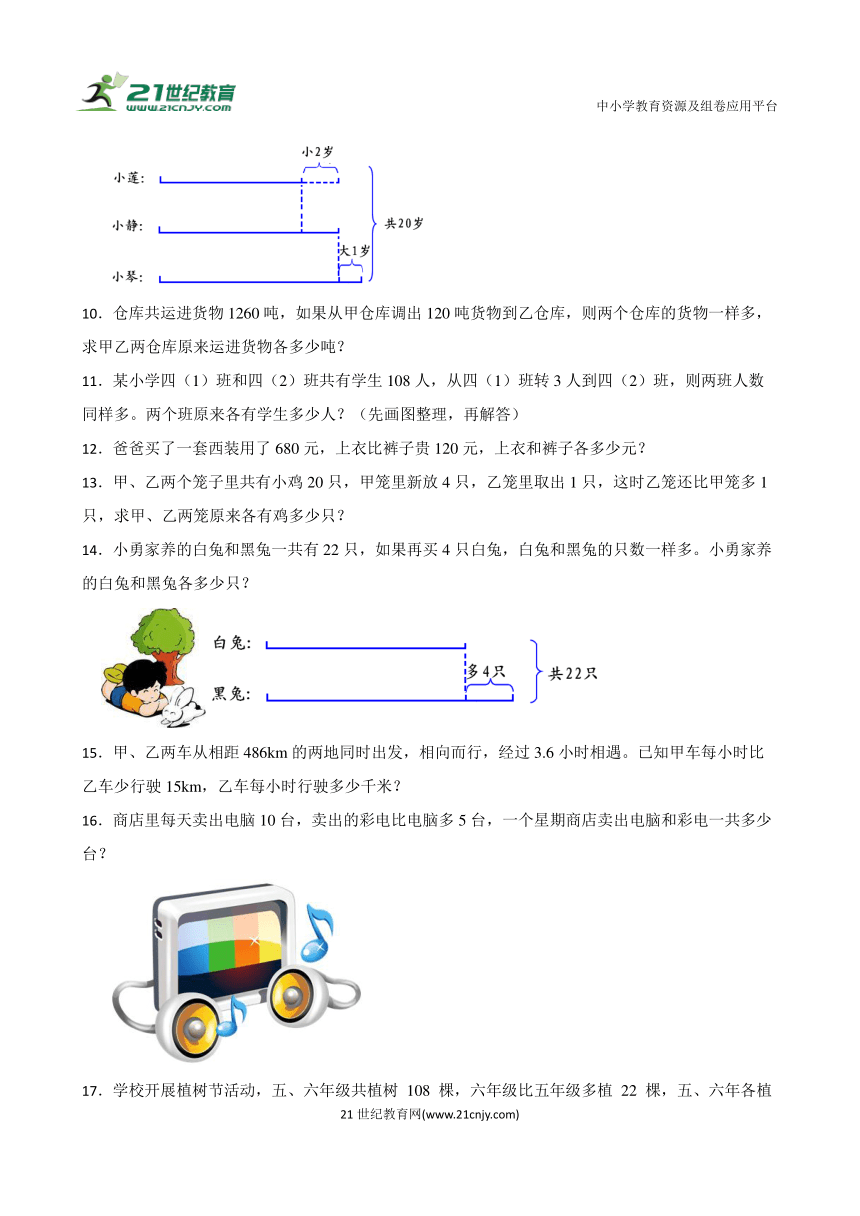
9.小琴、小静、小莲三人年龄和是20岁,小琴比小静大1岁,小莲比小静小2岁。三人的年龄各是几岁?
10.仓库共运进货物1260吨,如果从甲仓库调出120吨货物到乙仓库,则两个仓库的货物一样多,求甲乙两仓库原来运进货物各多少吨?
11.某小学四(1)班和四(2)班共有学生108人,从四(1)班转3人到四(2)班,则两班人数同样多。两个班原来各有学生多少人?(先画图整理,再解答)
12.爸爸买了一套西装用了680元,上衣比裤子贵120元,上衣和裤子各多少元?
13.甲、乙两个笼子里共有小鸡20只,甲笼里新放4只,乙笼里取出1只,这时乙笼还比甲笼多1只,求甲、乙两笼原来各有鸡多少只?
14.小勇家养的白兔和黑兔一共有22只,如果再买4只白兔,白兔和黑兔的只数一样多。小勇家养的白兔和黑兔各多少只?
15.甲、乙两车从相距486km的两地同时出发,相向而行,经过3.6小时相遇。已知甲车每小时比乙车少行驶15km,乙车每小时行驶多少千米?
16.商店里每天卖出电脑10台,卖出的彩电比电脑多5台,一个星期商店卖出电脑和彩电一共多少台?
17.学校开展植树节活动,五、六年级共植树 108 棵,六年级比五年级多植 22 棵,五、六年各植树多少棵?
(1)在线段图中标出已知条件。
(2)列式(108-22)÷2,求的是 。
列式(108+22)÷2,求的是 。
18.一篮苹果连篮子的质量共2100克,苹果的质量比篮子多1600克,苹果的质量为多少克?
19.哥哥今年14岁,妹妹今年8岁,当兄妹俩岁数的和是42岁时,俩人各应该是多少岁?
20.姐姐做自然练习比妹妹做算术练习多用48分钟,比妹妹做英语练习多用42分钟,妹妹做算术、英语两门练习共用了44分钟,那么妹妹做英语练习用了多少分钟?
21.甲的书比乙多9本,比丙多2本,乙、丙共有书47本。问:甲、乙、丙各有多少本书?
22.如果在乘电动扶梯的同时小明继续向上走需12秒到达楼上,如果在乘电动扶梯的同时小明逆着向下走需 秒到达楼下(千万别模仿!),那么电动扶梯不动时,小明徒步沿扶梯上楼需多少秒?
23.图书室里的故事书与科技书共有720本,又知故事书比科技书多160本,这两种图书各有多少本?
24.甲、乙两箱共有60千克水果,如果从甲箱取出5千克放入乙箱,则两箱水果一样重,乙箱有水果多少千克?
25.桃树和梨树一共有425棵,梨树比桃树多75棵,桃树有多少棵?
26.两箱图书共有66本,甲箱如果借出10本,就比乙箱少4本。甲、乙两箱原有图书各多少本?
27.亮亮为做热身活动,沿着长与宽相差15m的长方形操场跑了4圈,共跑了680m,操场的长与宽分别是多少米?
28.草地上有黑兔、白兔、灰兔共27只,黑兔比白兔多2只,灰兔比白免少2只。黑兔、白兔、灰兔各有多少只?
29.如图所示,若涂色部分甲的面积比涂色部分乙的面积大 求BC的长。
30.哥哥比弟弟大4岁,三年前两人的年龄之和是18岁.哥哥今年多少岁?
31.甲、乙、丙三个数的和是105,甲数比乙数多4,乙数比丙数多4,求丙数。
32.小明和小青一共有94张邮票,小青给小明7张后,两人邮票的张数同样多。小明和小青原来各有邮票多少张?(先把已知条件在线段图上表示出来,再解答)
33.甲、乙、丙三个班向希望工程捐赠图书.已知甲班1人捐6册,有2人各捐7册,其余人各捐11册;乙班有1人捐6册,3人各捐8册,其余人各捐10册;丙班有2人各捐4册,6人各捐7册,其余人各捐9册.已知甲班捐书总数比乙班多28册,乙班比丙班多101册.各班捐书总数都在400册与550册之间,问:每班各有多少人?
34.甲校原来比乙校多48人,为方便就近入学,甲校有若干人转入乙校,这时甲校反而比乙校少12人。甲校有多少人转入乙校?
35.有大、小两个油桶,一共装油24千克,两个油桶都倒出同样多的油后分别还剩9千克和5千克。问:原来大、 小两个油桶各装油多少千克?
36.四堆苹果共有46个,如果第一堆增加1个,第二堆减少2个,第三堆增加一倍,第四堆减少一半,那么这四堆苹果的个数相同,这四堆苹果原来各有多少个?
37.甲乙共储蓄32元,乙丙共储蓄30元,甲丙共储蓄22元,三人各储蓄多少元?
38.水果店运来2箱苹果,3箱梨,4箱桃子,一共164千克,每箱苹果比梨轻3千克,每箱桃子比苹果重5千克,苹果、梨、桃子每箱各重多少千克?
39.小军和小红一共集邮78张邮票,小红邮票的张数比小军少6张。小军和小红各集多少张邮票?
40.体育场有篮球、足球共78个,借给四(1)班2个足球后,足球仍比篮球多16个,体育场原有篮球、足球各多少个?
41.甲、乙两校共有学生1050人,部分学生因搬家需要转学,已知由甲校转入乙校20人,这样甲校比乙校还多10人,求两校原来有学生多少人?
42.已知a、b、c是非负数,且2a+3b+c=10,a+b-c=4,如果S=2a+b-2c,那么S的最大值与最小值之差是多少
43.今年小明10岁,小强15岁,当两人的年龄和为49岁时,两人各是多少岁?
44.红旗小学三年级和四年级共有学生160人,四年级比三年级多20人.三年级和四年级各有学生多少人?
45.王婷和李红一共有画片146张,王婷给李红23张后两人画片的张数一样多,两人原来各有画片多少张 (先画图表示再解答)
46.学校买5个足球和5个排球一共用去525元。如果排球的单价比足球便宜15元/个,足球和排球的单价各是多少元/个?
47.饲养场养鸡和鸭一共126只,卖掉30只鸡后,鸡和鸭的只数同样多。饲养场原来养鸭多少只?养鸡多少只?
48.小华和小敏共有铅笔25枝,如果小华用去4枝,小敏用去3枝,那么小华还比小敏多2枝,小华和小敏原来各有多少枝铅笔?
49.甲、乙两个工程队共1980人,甲队为了支援乙队,抽出285人调入乙队,这时乙队人数还比甲队少24人。甲、乙两队原有工人多少人?
50.小玉家养鸡和鸭一共68只,卖掉20只鸡后,鸡和鸭的只数同样多。她家原来养鸭多少只?养鸡多少只?
参考答案及试题解析
1.解:分母:(29+7)÷2=18,分子:29-18=11
或:分子:(29-7)÷2=11,分子:29-11=18
答:这个分数是 。
【解析】(和+差)÷2=大数,大数-差=小数,因为是真分数,所以大数是分母,小数是分子。
2.解:小红:(84﹣14)÷2
=70÷2
=35(张)
小明:84﹣35=49(张)
答:小明收集49张邮票,小红收集了35张邮票
【解析】用一共的邮票数减14张,即是小红收集邮票的张数的2倍,用除法可得小红收集邮票的张数,进而求得小明收集邮票的张数.
3.解:哥哥和弟弟的年龄差:6+8=14(岁)
(38-5+3+14)÷2
=(36+14)÷2
=50÷2
=25(岁)
25-14=11(岁)
答:哥哥今年25岁,弟弟今年11岁。
【解析】根据题意,哥哥今年的年龄=(今年两人的年龄和+两人的年龄差)÷2,弟弟的年龄=(今年两人的年龄和-两人的年龄差)÷2,分别代入数值计算即可。
4.解:270÷2=135(本)
135+38=173(本)
135-38=97(本)
答:原来两层书架上的书各有173本、97本。
【解析】现在两层书架上的本数相等,总数仍然是270本,所以用270除以2即可求出现在每层的本数。用现在第一层的本数加上38即可求出第一层原来的本数;用现在第二层的本数减去38即可求出原来第二层的本数。
5.解:
(86+16)÷2
=102÷2
=51(张)
51-16=35(张)
答:王星有画片51张,张宁有35张。
【解析】和差问题: (和+差)÷2=较大数,(和-差)÷2=较小数。
6.解:宽:(72÷2-4)÷2
=32÷2
=16(米)
长:16+4=20(米)
面积:16×20=320(平方米)
答:这个菜园的面积是320平方米。
【解析】先按和差问题求出长方形的长宽;长方形菜园周长÷2=长宽的和,(长宽的和-长宽的差)÷2=较小的数,较小的数+差=较大的数;长方形面积=长×宽。
7.解:2分钟-2秒=1分钟58秒
答:经过1分钟58秒正巧也是满满一瓶小虫。
【解析】如果刚开始瓶里有1只小虫,每隔2秒钟分裂一次,第一次就分裂成2个,第二次就分裂成4个……这样2分钟就正好有了满满一瓶小虫。如果瓶里开始就放有2只小虫,那么第一次就分裂成4个,和原来比少了1个分裂成两个的2秒,直接已经有了2个。这样如果瓶里有2只小虫,就会原来的时间少2秒,需要1分钟58秒就分裂成了满满一瓶小虫。
8.解:甲:(27+3)÷2
=30÷2
=15(岁)
乙:15-3=12(岁)
答:甲15岁,乙12岁.
【解析】假如把乙的岁数加上3,两人岁数就相等,此时两人的年龄和是(27+3),用年龄和除以2即可求出甲的年龄,进而求出乙的年龄即可.
9.解:20+(2-1)
=20+1
=21(岁)
21÷3=7(岁)
7+1=8(岁)
7-2=5(岁)
答:小静7岁,小琴8岁,小莲5岁。
【解析】以小静为标准,小琴比小静大1岁,小莲比小静小2岁,把小琴比小静大的1岁,补给小莲,那么小琴现在和小静一样大,而小莲比小静就只小1岁,如果再加上1岁,也和小静一样大。那么现在小静年龄的3倍就应该是21岁;小静的年龄=21÷3=7岁,小琴现在的年龄是=小静的年龄+1岁,小莲现在的年龄=小静的年龄-2岁。
10.解:设甲仓库原来运进货物x吨,则乙仓库运进货物(1260﹣x)吨,
x﹣120=1260﹣x+120
2x=1500
x=750
1260﹣750=510(吨)
答:甲仓库原来运进货物750吨,乙仓库原来运进货物510吨.
【解析】设甲仓库原来运进货物x吨,则乙仓库运进货物(1260﹣x)吨,根据等量关系:甲仓库原来运进货物﹣120吨=乙仓库原来运进货物+120吨,列方程解答即可.
11.解:
3×2=6(人)
(108-6)÷2
=102÷2
=51(人)
51+6=57(人)
答:四(1)班有57人,四(2)班有51人。
【解析】从四(1)班转3人到四(2)班,则两班人数同样多,说明从四(1)班比四(2)班多6人;根据和差问题的解法解答,(和-差)÷2=小数,小数+差=大数。
12.解:(680+120)÷2
=800÷2
=400(元)
400-120=280(元)
答:上衣400元,裤子280元。
【解析】和差问题:(和+差)÷2=大数,大数-差=小数,据此解答。
13.解:4+1+1
=5+1
=6(只)
(20-6)÷2
=14÷2
=7(只)
7+6=13(只)
答:甲笼里原有小鸡7只,乙笼里原有小鸡13只。
【解析】甲、乙两个笼里小鸡相差的只数=4+1+1=6只,甲笼里原有小鸡的只数=(总只数-6只)÷2,乙笼里原有小鸡的只数=甲笼里原有小鸡的只数+6只。
14.解:(22-4)÷2
=18÷2
=9(只)
9+4=13(只)
答:小勇家养的白兔有9只,黑兔有13只。
【解析】小勇家养白兔的只数=(总只数-4只)÷2;养黑兔的只数=小勇家养白兔的只数+4只。
15.解:486÷3.6=135(千米/时)
(135+15)÷2
=150÷2
=75(千米/时)
答:乙车每小时行驶75千米。
【解析】路程÷相遇时间=甲、乙两车的速度和;甲、乙两车的速度差是15,按和差问题计算,(和+差)÷2=大数,据此解答。
16.解:(10+5+10)×7
=(15+10)×7
=25×7
=175(台)
答:一个星期商店卖出电脑和彩电一共175台。
【解析】一个星期商店卖出电脑和彩电的总台数=(平均每天卖出电脑的台数+平均每天卖出彩电的台数)×卖的天数;其中,平均每天卖出彩电的台数=平均每天卖出电脑的台数+5台。
17.(1)解:
(2)五年级植树的棵数;六年级植树的棵数
【解析】解:(2)列式(108-22)÷2,求的是五年级植树的棵数;
列式(108+22)÷2,求的是六年级植树的棵数。
故答案为:(2)五年级植树的棵数;六年级植树的棵数。
【分析】(1)五、六年级共植树 108 棵,六年级比五年级多植 22 棵,把这两个条件填在小括号里面;
(2)已知两个数的和与两个数的差,可以用和差问题解决:(和+差)÷2=较大数,(和-差)÷2=较小数。
18.解:(2100+1600)÷2
=3700÷2
=1850(克)
答:苹果的质量为1850克。
【解析】(和+差)÷2=较大数,和-较大数=较小数。
19.解:14-8=6(岁)
(42-6)÷2
=36÷2
=18(岁)
18+6=24(岁)
答:那时哥哥24岁,妹妹18岁。
【解析】无论过去几年,两个人的年龄差不变,那时妹妹的年龄=(总岁数-6岁)÷2,哥哥的年龄=妹妹的年龄+6岁。
20.解:48-42=6(分)
(44+6)÷2
=50÷2
=25(分)
答:妹妹做英语练习用了25分钟。
【解析】“姐姐做自然练习比妹妹做算术练习多用48分钟,比妹妹做英语练习多用42分钟”,由此可以推出妹妹做算术练习比做英语练习少用时间:48-42=6分钟,则妹妹做英语练习的时间=(妹妹做算术、英语两门练习共用的时间+6分钟)÷2。
21.解:9-2=7(本)
(47-7)÷2
=40÷2
=20(本)
20+9=29(本)
20+7=27(本)
答:甲有29本,乙有20本,丙有27本。
【解析】甲的书比乙多9本,比丙多2本,说明乙的书比丙少9-2=7本,乙有书的本数=(乙、丙共有书的本数-7本)÷2,甲有书的本数=乙有书的本数+9本,丙有书的本数=乙有书的本数+7本。
22.解:小明徒步走的速度是 ,所以小明徒步上楼需 (秒)。
答:小明徒步沿扶梯上楼需16秒。
【解析】扶梯+小明走的速度和=1÷12=,小明走的速度-扶梯的速度差为:1÷24=,两个小明走的速度和为:+=,小明的速度:÷2=,时间=1÷=16(秒)
【分析】和差问题,大数+小数=和,大数-小数=差,(和+差)÷2=大数,(和-差)÷2=小数
23.解:(720-160)÷2
=560÷2
=280(本)
280+160=440(本)
答:科技书有280本,故事书有440本。
【解析】科技书的本数=(总本数-故事书比科技书多的本数)÷2;故事书的本数=科技书的本数+160本。
24.解:乙箱原有水果:
(60﹣5×2)÷2
=50÷2
=25(千克),
答:乙箱有水果25千克.
【解析】由“从甲箱中取出5千克放入乙箱,两箱水果就一样重”,可知甲箱比乙箱原来重5×2=10(千克),然后根据和差问题的解法,解答即可.
25.解:(425-75)÷2=175(棵)
答:桃树有175棵。
【解析】本题已知桃树和梨树的和与差,采取和差公式,桃树(小数)=(和-差)÷2;梨树(大数)=(和+差)÷2;据此代入数值计算即可。
26.解:10-4=6(本)
(66-6)÷2
=60÷2
=30(本)
30+6=36(本)
答:甲箱原有图书36本、乙箱原有图书30本。
【解析】甲箱如果借出10本,就比乙箱少4本,则说明原来甲箱比乙箱多10-4=6本,乙箱原有图书的本数=(总本数-6本)÷2、甲箱原有图书的本数=乙箱原有图书的本数+6本。
27.解:长方形的周长:680÷4=170(米)
长方形长宽的和:170÷2=85(米)
(85+15)÷2=100÷2=50(米)
50-15=35(米)
答:操场的长是50米,宽是35米。
【解析】和差问题:(和+差)÷2=较大数,和-较大数=较小数。
28.解:画图分析:
27÷3=9(只) 9+2=11(只) 9-2=7(只) 答:白兔有9只,黑兔有11只,灰兔有7只。
【解析】黑兔比白兔多2只,灰兔比白免少2只,把黑兔比白兔多的补到灰兔比白免少的部分,这样黑兔、白兔、灰兔共27只也可以看成是3倍白兔这么多,因此可以先求出白兔的只数=27÷3=9只,黑兔的只数=白兔的只数+2只,灰兔的只数=白兔的只数-2只。
29.150×2÷20=15(cm)
答:BC长15厘米。
【解析】 涂色部分甲的面积比涂色部分乙的面积大 如果甲加上一个空白部分,乙也加一个相同的空白部分,就是半圆的面积比三角形面积大7平方厘米。已知圆的半径可以求出半圆的面积,继而求出三角形的面积,而三角形的高是圆的直径,所以可以求出三角形底边BC的长度。
30.解:今年两人的年龄之和:18+3+3=24(岁)
弟弟的年龄:(24+4) ÷2=14(岁)
答:哥哥今年14岁。
【解析】用两人三年前的年龄之和加上两个3即可求出今年两人的年龄。如果把弟弟的年龄加上4就和哥哥同样多,所以用两人的年龄和加上4,再除以2即可求出哥哥今年的年龄。
31.解:4+4+4
=8+4
=12
(105-12)÷3
=93÷3
=31
答:丙数是31。
【解析】已知甲数比乙数多4,乙数比丙数多4,可求出甲数比丙数多4+4=8;如果甲数少8,乙数少4,则甲、乙、丙三数相等,差正好是丙的3倍,除以3便可求出丙数。
32.解:
7+7=14(张)
(94-14)÷2=40(张)
94-40=54(张)
答:小明原来有40张邮票,小青原来有54张邮票。
【解析】小青给小明7张后,两人邮票的张数同样多,说明小青原来比小明多2个7张,那么小明原来有邮票的张数=(他们一共有邮票的张数-多的张数)÷2,小青原来有邮票的张数=他们一共有邮票的张数-小明原来有邮票的张数,据此代入数值作答即可。
33.解:由题目条件,甲班捐书最多,丙班最小,甲班比丙班多捐28+101=129(册);
又各班捐书总数都在400册与550册之间,则丙班捐书不少于400册,所以甲班捐书在529~550册之间;
设甲班有x人,乙班有y人,丙班有z人,则甲班共捐书(6+2×7+11×(x-3))册,乙班共捐书(6+3×8+10×(y-4))册,丙班共捐书(2×4+6×7+9×(z-8))册;
依题意,有
解之,得
答:甲班有51人,乙班有53人,丙班有49人。
【解析】本题考查了三元一次方程组的应用,解题的关键是:甲班比丙班多捐28+101=129(册)。根据题意,甲班捐书最多,丙班最小,甲班比丙班多捐28+101=129(册);又各班捐书总数都在400册与550册之间,则丙班捐书不少于400册,所以甲班捐书在529~550册之间。
34.解:48÷2=24(人)
12÷2=6(人)
24+6=30(人)
答:甲校有30人转入乙校。
【解析】根据“甲校原来比乙校多48人”可知甲校转入24人到乙校时,两所学校的人数一样。当甲校继续有同学转入到乙校时,每转入一个同学,甲校就比乙校少2人。当再从甲校转入6人到乙校时,甲校就比乙校少12人,所以甲校一共转入乙校 (人)时,甲校就比乙校少12人。
35.解:9-5=4(千克)
(24-4)÷2
=20÷2
=10(千克)
10+4=14(千克)
答:原来小油桶装油10千克,大油桶装油14千克。
【解析】两个油桶都倒出同样多的油后分别还剩9千克和5千克,那么也就是说大桶比小桶多4千克的油;原来小油桶装油的质量=(总质量-4千克)÷2,大油桶装油的质量=小油桶装油的质量+4千克。
36.解:设第一堆苹果原来有x个,则第二堆有(x+3)个,第三堆有(x+1)个,第四堆有2(x+1)个。
x+x+3+(x+1)+2(x+1)=46
4x+5=46
x=40÷4
x=9
第二堆:9+3=12(个);
第三堆:×(9+1)=5(个);
第四堆:2×(9+1)=20(个)。
答:这四堆苹果原来各有9个,12个,5个,20个。
【解析】分析题意可得:第一堆原有苹果数+1=第二堆原有苹果数-2,则第二堆原有苹果数=第一堆原有苹果数+1+2=第一堆原有苹果数+3;第一堆原有苹果数+1=第三堆原有苹果数×2,则第三堆原有苹果数=(第一堆原有苹果数+1)×;第一堆原有苹果数+1=第四堆原有苹果数×,则第四堆原有苹果数=(第一堆原有苹果数+1)×2;
第一堆原有苹果数+(第一堆原有苹果数+3)+(第一堆原有苹果数+1)×+(第一堆原有苹果数+1)×2=四堆苹果总数,据此关系式设第一堆苹果原来有x个,则第二堆有(x+3)个,第三堆有(x+1)个,第四堆有2(x+1)个,列方程即可解答。
37.解:(32+22+30)÷2
=(54+30)÷2
=84÷2
=42(元)
丙:42-32=10(元)
甲:42-30=12(元)
乙:42-22=20(元)
答:甲、乙、丙各储蓄12元、20元、10元。
【解析】甲储蓄的钱数=三人储蓄的钱数和-乙丙共储蓄的钱数、乙储蓄的钱数=三人储蓄的钱数和-甲丙共储蓄的钱数、丙储蓄的钱数=三人储蓄的钱数和-甲乙共储蓄的钱数;其中,三人储蓄的钱数和=(乙丙共储蓄的钱数+甲丙共储蓄的钱数+甲乙共储蓄的钱数)÷2。
38.解:
苹果 (164﹣3×3﹣5×4)÷(2+3+4)
=(164﹣9﹣20)÷9
=135÷9
=15(千克)
梨 15+3=18(千克)
桃子15+5=20(千克)
答:苹果每箱重15千克、梨每箱重18千克、桃子每箱重20千克.
【解析】根据“水果店运来每箱苹果比梨轻3千克,每箱桃子比苹果重5千克”,可知梨和桃子每箱都比苹果重,假设运来的都是苹果,则从总质量164千克里去 掉3箱梨比3箱苹果多的和4箱桃子比4箱苹果多的质量,用假设的苹果总质量除以假设的苹果总箱数,求出每箱苹果的质量,进而求出梨和桃子每箱的质量.
39.解:(78-6)÷2
=72÷2
=36(张)
36+6=42(张)
答:小红36张,小军42张。
【解析】小红集邮的张数=(两人集邮的总张数-6张)÷2;小军集邮的张数=小红集邮的张数+6张。
40.解:[78﹣(16+2)]÷2
=[78﹣18]÷2
=60÷2
=30(个)
78﹣30=48(个)
答:体育场原有篮球30个,足球48个。
【解析】借给四(1)班2个足球后,足球仍比篮球多16个,可知体育场原有足球比篮球多16+2=18(个),用总数78减18再除以2即可得篮球的个数,再求足球个数即可。
41.解:20×2+10
=40+10
=50(人)
(1050-50)÷2
=1000÷2
=500(人)
500+50=550(人)
答:乙校原来有学生500人,甲校原来有学生550人。
【解析】乙校原来有学生的人数=(总人数-由甲校转入乙校的人数×2-10人)÷2,甲校原来有学生的人数=乙校原来有学生的人数+50人。
42.解:根据题意得:
将①-②×2得:b=2-3c③,
将③代入②中得:a=2+4c ,
S= 2a +b-2c=2(2+4c)+2-3c-2c =6+3c;
因为a、b、c是非负数,所以0≤c≤,0≤2-3c,
由于S=6+3c,可知,S随c的增大而增大,
当c=0时,S=6+3c=6,
当c=时,S=6+3c=6+3×=10.5,
则S的最大值与最小值之差是10.5-6=4.5。
答:S的最大值与最小值之差是4.5
【解析】根据题意建立方程组,加减消元法得到用c表示b的代数式,再代入方程组可以得到用c表示a的代数式,化简 S=2a+b-2c=6+3c,因为a、b、c是非负数,可以得到c的范围,根据S随c的增大而增大,可得S的最大值与最小值,即可解答。
43.解:15-10=5(岁)
(49+5)÷2
=54÷2
=27(岁)
(49-5)÷2
=44÷2
=22(岁)
答:当两人的年龄和为49岁时,小明22岁,小强27岁。
【解析】本题可先求出两人的年龄差,又已知两人的年龄和,这道题就变为一道“和差”问题。
44.解:四年级:
(160+20)÷2
=180÷2
=90(人)
三年级:
160﹣90=70(人)
答:三年级有70人,四年级有90人。
【解析】假如把三年级的人数加上20人,那么两个年级的人数就相等,总人数也会增加20人,因此用增加后的总人数除以2即可求出四年级的人数,进而求出三年级的人数即可。
45.解:
146÷2=73(张)
73+23=96(张)
73-23=50(张)
答:王婷原有画片96张,李红原有画片50张。
【解析】两人同样多时的张数=画片的总数÷2,王婷原有画片是张数=同样多时的张数+王婷给李红的张数,李红原有画片是张数=同样多时的张数-王婷给李红的张数。
46.解:525÷5=105(元)
(105+15)÷2=60(元)
60-15=45(元)
答:足球的单价是60元,排球的单价是45元。
【解析】此题属于和差问题:一个足球和一个排球的差是15元;
5个足球和5个排球一共用去525元,据此求出一个足球和一个排球的和;
(和+差)÷2=大数,大数-差=小数,据此解答。
47.解:126-30=96(只)
鸭:96÷2=48(只)
鸡:126-48=78(只)
答:饲养场原来养鸭48只,养鸡78只。
【解析】分析题意可知:鸡、鸭总数减去30只鸡后,鸡、鸭只数相等,所以,(鸡、鸭总数-30)÷2=鸭的只数,鸡、鸭总数-鸭的只数=鸡的只数。
48.解:4-3+2
=1+2
=3(枝)
(25-3)÷2
=22÷2
=11(枝)
11+3=14(枝)
答:小敏原来有11枝铅笔,小华原来有14枝铅笔。
【解析】如果小华用去4枝,小敏用去3枝,那么小华还比小敏多2枝,这就说明原来小华的铅笔比小敏的铅笔多3枝;小敏原来有铅笔的枝数=(总枝数-3枝)÷2,小华原来有铅笔的枝数=小敏原来有铅笔的枝数+3枝。
49.甲队原有人数:(285×2+24+1980)÷2=1287(人)
乙队原有人数:1287-594=693(人)
答:甲队原有1287人,乙队原有693人。
【解析】根据 “ 甲、乙两个工程队共1980人, ”可知甲、乙两个工程队人数和为1980人,甲队抽出285人调入乙队,这时乙队人数还比甲队少24人 ,可知甲队和乙队人数差是285×2+24=594人,所以根据和差公式,“(和+差) ÷2=大数,大数-差=小数”的公式,即可求出两队原有的人数。
50.解:(68-20)÷2
=48÷2
=24(只)
24+20=44(只)
答:她家原来养鸭20只,养鸡44只。
【解析】把卖掉的减去后,鸡的只数和鸭的只数相同,除以2就是鸭的只数;鸭的只数加上20只,就是鸡的只数。
21世纪教育网(www.21cnjy.com)
小升初奥数思维之典型应用题精讲精练讲义(通用版)
专题11 和差问题
【第一部分:知识归纳】
一、基本概念
1、和差问题是指已知两个数的和与差,求这两个数的数学问题。这是小学阶段最基础的应用题类型之一,也是解决更复杂问题的重要基础。
2、核心公式:
较大数 = (和 + 差) ÷ 2
较小数 = (和 - 差) ÷ 2
二、解题四步法
步骤1:判断题型
确认题目中是否明确给出或隐含两个数的和与差
步骤2:画线段图
较大数:|___________|___|
较小数:|___________|
(差的部分用不同颜色标出)
步骤3:选择公式
根据所求的是较大数还是较小数选择对应公式
步骤4:计算验证
将结果代入原题验证是否符合和差关系
三、五大经典题型
题型1:基础型
例题:甲乙两数之和为58,差为12,求这两个数。
解答:较大数 = (58 + 12) ÷ 2 = 35
较小数 = (58 - 12) ÷ 2 = 23
题型2:隐含差型
例题:
哥哥和妹妹共有48元,哥哥给妹妹6元后两人钱数相等。原来各有多少钱?
解答:差 = 6 × 2 = 12元(给6元相当于差减少12元)
哥哥原有 = (48 + 12) ÷ 2 = 30元
妹妹原有 = 48 - 30 = 18元
题型3:多对象型
例题:
甲乙丙三数之和为120,甲比乙大10,乙比丙大8,求这三个数。
解答:设丙为x,则乙=x+8,甲=x+18
x+(x+8)+(x+18)=120 → x=94/3≈31.33
∴ 丙≈31.33,乙≈39.33,甲≈49.33
题型4:年龄问题
例题:
父子年龄和是50岁,5年后父亲比儿子大24岁。现在两人各多少岁?
解答:年龄差不变:24岁
父亲现在 = (50 + 24) ÷ 2 = 37岁
儿子现在 = 50 - 37 = 13岁
题型5:图形应用
例题:
长方形周长40cm,长比宽多4cm,求面积。
解答:长+宽=40÷2=20cm
长=(20+4)÷2=12cm
宽=20-12=8cm
面积=12×8=96cm
四、易错点与技巧
1、常见错误
忽略隐含差:如"给多少后相等"类问题
单位不统一:和与差的单位不一致
年龄差不变:忘记年龄差是固定值
公式记反:混淆较大数和较小数的公式
2、解题技巧
画图法:用线段图直观展示数量关系
举例法:用具体数字验证思路
方程法:设未知数建立简单方程
验证法:计算后检查是否满足原条件
【第二部分:能力提升】
1.一个真分数的分子和分母的和是29,分母与分子的差是7,这个真分数是多少?
2.小明和小红共收集邮票84张,小明收集的邮票比小红多14张,小明和小红各收集多少张邮票?
3.哥哥6年前的岁数等于弟弟8年后的岁数.哥哥5年后与弟弟3年前的年龄和是38岁.求兄弟二人今年各几岁
4.某市红领巾小学图书室里有个书架有两层,共有图书270本,如果从第一层书架上拿38本给第二层书架,则两层书架上的书就相等。求原来两层书架上的书各有多少本?
5.张宁和王星一共有画片86张。王星比张宁多16张。两人各有画片多少张?(先把已知条件在线段图上表示出来,再解答)
6.一个长方形菜园周长是72米,宽比长少4米。这个菜园的面积是多少平方米?
7.有一种小虫,每隔2秒钟分裂一次。分裂后的2只新的小虫经过2秒钟后又会分裂。如果最初瓶中只有1只小虫,那么2秒后变2只,再过2秒后就变4只……2分钟后,正好满满一瓶小虫。现在这个瓶内最初放入2只这样的小虫。经过多长时间,正巧也是满满一瓶小虫?
8.甲、乙两人的年龄之和为27岁,甲比乙大3岁,那么甲、乙两人各多大?
9.小琴、小静、小莲三人年龄和是20岁,小琴比小静大1岁,小莲比小静小2岁。三人的年龄各是几岁?
10.仓库共运进货物1260吨,如果从甲仓库调出120吨货物到乙仓库,则两个仓库的货物一样多,求甲乙两仓库原来运进货物各多少吨?
11.某小学四(1)班和四(2)班共有学生108人,从四(1)班转3人到四(2)班,则两班人数同样多。两个班原来各有学生多少人?(先画图整理,再解答)
12.爸爸买了一套西装用了680元,上衣比裤子贵120元,上衣和裤子各多少元?
13.甲、乙两个笼子里共有小鸡20只,甲笼里新放4只,乙笼里取出1只,这时乙笼还比甲笼多1只,求甲、乙两笼原来各有鸡多少只?
14.小勇家养的白兔和黑兔一共有22只,如果再买4只白兔,白兔和黑兔的只数一样多。小勇家养的白兔和黑兔各多少只?
15.甲、乙两车从相距486km的两地同时出发,相向而行,经过3.6小时相遇。已知甲车每小时比乙车少行驶15km,乙车每小时行驶多少千米?
16.商店里每天卖出电脑10台,卖出的彩电比电脑多5台,一个星期商店卖出电脑和彩电一共多少台?
17.学校开展植树节活动,五、六年级共植树 108 棵,六年级比五年级多植 22 棵,五、六年各植树多少棵?
(1)在线段图中标出已知条件。
(2)列式(108-22)÷2,求的是 。
列式(108+22)÷2,求的是 。
18.一篮苹果连篮子的质量共2100克,苹果的质量比篮子多1600克,苹果的质量为多少克?
19.哥哥今年14岁,妹妹今年8岁,当兄妹俩岁数的和是42岁时,俩人各应该是多少岁?
20.姐姐做自然练习比妹妹做算术练习多用48分钟,比妹妹做英语练习多用42分钟,妹妹做算术、英语两门练习共用了44分钟,那么妹妹做英语练习用了多少分钟?
21.甲的书比乙多9本,比丙多2本,乙、丙共有书47本。问:甲、乙、丙各有多少本书?
22.如果在乘电动扶梯的同时小明继续向上走需12秒到达楼上,如果在乘电动扶梯的同时小明逆着向下走需 秒到达楼下(千万别模仿!),那么电动扶梯不动时,小明徒步沿扶梯上楼需多少秒?
23.图书室里的故事书与科技书共有720本,又知故事书比科技书多160本,这两种图书各有多少本?
24.甲、乙两箱共有60千克水果,如果从甲箱取出5千克放入乙箱,则两箱水果一样重,乙箱有水果多少千克?
25.桃树和梨树一共有425棵,梨树比桃树多75棵,桃树有多少棵?
26.两箱图书共有66本,甲箱如果借出10本,就比乙箱少4本。甲、乙两箱原有图书各多少本?
27.亮亮为做热身活动,沿着长与宽相差15m的长方形操场跑了4圈,共跑了680m,操场的长与宽分别是多少米?
28.草地上有黑兔、白兔、灰兔共27只,黑兔比白兔多2只,灰兔比白免少2只。黑兔、白兔、灰兔各有多少只?
29.如图所示,若涂色部分甲的面积比涂色部分乙的面积大 求BC的长。
30.哥哥比弟弟大4岁,三年前两人的年龄之和是18岁.哥哥今年多少岁?
31.甲、乙、丙三个数的和是105,甲数比乙数多4,乙数比丙数多4,求丙数。
32.小明和小青一共有94张邮票,小青给小明7张后,两人邮票的张数同样多。小明和小青原来各有邮票多少张?(先把已知条件在线段图上表示出来,再解答)
33.甲、乙、丙三个班向希望工程捐赠图书.已知甲班1人捐6册,有2人各捐7册,其余人各捐11册;乙班有1人捐6册,3人各捐8册,其余人各捐10册;丙班有2人各捐4册,6人各捐7册,其余人各捐9册.已知甲班捐书总数比乙班多28册,乙班比丙班多101册.各班捐书总数都在400册与550册之间,问:每班各有多少人?
34.甲校原来比乙校多48人,为方便就近入学,甲校有若干人转入乙校,这时甲校反而比乙校少12人。甲校有多少人转入乙校?
35.有大、小两个油桶,一共装油24千克,两个油桶都倒出同样多的油后分别还剩9千克和5千克。问:原来大、 小两个油桶各装油多少千克?
36.四堆苹果共有46个,如果第一堆增加1个,第二堆减少2个,第三堆增加一倍,第四堆减少一半,那么这四堆苹果的个数相同,这四堆苹果原来各有多少个?
37.甲乙共储蓄32元,乙丙共储蓄30元,甲丙共储蓄22元,三人各储蓄多少元?
38.水果店运来2箱苹果,3箱梨,4箱桃子,一共164千克,每箱苹果比梨轻3千克,每箱桃子比苹果重5千克,苹果、梨、桃子每箱各重多少千克?
39.小军和小红一共集邮78张邮票,小红邮票的张数比小军少6张。小军和小红各集多少张邮票?
40.体育场有篮球、足球共78个,借给四(1)班2个足球后,足球仍比篮球多16个,体育场原有篮球、足球各多少个?
41.甲、乙两校共有学生1050人,部分学生因搬家需要转学,已知由甲校转入乙校20人,这样甲校比乙校还多10人,求两校原来有学生多少人?
42.已知a、b、c是非负数,且2a+3b+c=10,a+b-c=4,如果S=2a+b-2c,那么S的最大值与最小值之差是多少
43.今年小明10岁,小强15岁,当两人的年龄和为49岁时,两人各是多少岁?
44.红旗小学三年级和四年级共有学生160人,四年级比三年级多20人.三年级和四年级各有学生多少人?
45.王婷和李红一共有画片146张,王婷给李红23张后两人画片的张数一样多,两人原来各有画片多少张 (先画图表示再解答)
46.学校买5个足球和5个排球一共用去525元。如果排球的单价比足球便宜15元/个,足球和排球的单价各是多少元/个?
47.饲养场养鸡和鸭一共126只,卖掉30只鸡后,鸡和鸭的只数同样多。饲养场原来养鸭多少只?养鸡多少只?
48.小华和小敏共有铅笔25枝,如果小华用去4枝,小敏用去3枝,那么小华还比小敏多2枝,小华和小敏原来各有多少枝铅笔?
49.甲、乙两个工程队共1980人,甲队为了支援乙队,抽出285人调入乙队,这时乙队人数还比甲队少24人。甲、乙两队原有工人多少人?
50.小玉家养鸡和鸭一共68只,卖掉20只鸡后,鸡和鸭的只数同样多。她家原来养鸭多少只?养鸡多少只?
参考答案及试题解析
1.解:分母:(29+7)÷2=18,分子:29-18=11
或:分子:(29-7)÷2=11,分子:29-11=18
答:这个分数是 。
【解析】(和+差)÷2=大数,大数-差=小数,因为是真分数,所以大数是分母,小数是分子。
2.解:小红:(84﹣14)÷2
=70÷2
=35(张)
小明:84﹣35=49(张)
答:小明收集49张邮票,小红收集了35张邮票
【解析】用一共的邮票数减14张,即是小红收集邮票的张数的2倍,用除法可得小红收集邮票的张数,进而求得小明收集邮票的张数.
3.解:哥哥和弟弟的年龄差:6+8=14(岁)
(38-5+3+14)÷2
=(36+14)÷2
=50÷2
=25(岁)
25-14=11(岁)
答:哥哥今年25岁,弟弟今年11岁。
【解析】根据题意,哥哥今年的年龄=(今年两人的年龄和+两人的年龄差)÷2,弟弟的年龄=(今年两人的年龄和-两人的年龄差)÷2,分别代入数值计算即可。
4.解:270÷2=135(本)
135+38=173(本)
135-38=97(本)
答:原来两层书架上的书各有173本、97本。
【解析】现在两层书架上的本数相等,总数仍然是270本,所以用270除以2即可求出现在每层的本数。用现在第一层的本数加上38即可求出第一层原来的本数;用现在第二层的本数减去38即可求出原来第二层的本数。
5.解:
(86+16)÷2
=102÷2
=51(张)
51-16=35(张)
答:王星有画片51张,张宁有35张。
【解析】和差问题: (和+差)÷2=较大数,(和-差)÷2=较小数。
6.解:宽:(72÷2-4)÷2
=32÷2
=16(米)
长:16+4=20(米)
面积:16×20=320(平方米)
答:这个菜园的面积是320平方米。
【解析】先按和差问题求出长方形的长宽;长方形菜园周长÷2=长宽的和,(长宽的和-长宽的差)÷2=较小的数,较小的数+差=较大的数;长方形面积=长×宽。
7.解:2分钟-2秒=1分钟58秒
答:经过1分钟58秒正巧也是满满一瓶小虫。
【解析】如果刚开始瓶里有1只小虫,每隔2秒钟分裂一次,第一次就分裂成2个,第二次就分裂成4个……这样2分钟就正好有了满满一瓶小虫。如果瓶里开始就放有2只小虫,那么第一次就分裂成4个,和原来比少了1个分裂成两个的2秒,直接已经有了2个。这样如果瓶里有2只小虫,就会原来的时间少2秒,需要1分钟58秒就分裂成了满满一瓶小虫。
8.解:甲:(27+3)÷2
=30÷2
=15(岁)
乙:15-3=12(岁)
答:甲15岁,乙12岁.
【解析】假如把乙的岁数加上3,两人岁数就相等,此时两人的年龄和是(27+3),用年龄和除以2即可求出甲的年龄,进而求出乙的年龄即可.
9.解:20+(2-1)
=20+1
=21(岁)
21÷3=7(岁)
7+1=8(岁)
7-2=5(岁)
答:小静7岁,小琴8岁,小莲5岁。
【解析】以小静为标准,小琴比小静大1岁,小莲比小静小2岁,把小琴比小静大的1岁,补给小莲,那么小琴现在和小静一样大,而小莲比小静就只小1岁,如果再加上1岁,也和小静一样大。那么现在小静年龄的3倍就应该是21岁;小静的年龄=21÷3=7岁,小琴现在的年龄是=小静的年龄+1岁,小莲现在的年龄=小静的年龄-2岁。
10.解:设甲仓库原来运进货物x吨,则乙仓库运进货物(1260﹣x)吨,
x﹣120=1260﹣x+120
2x=1500
x=750
1260﹣750=510(吨)
答:甲仓库原来运进货物750吨,乙仓库原来运进货物510吨.
【解析】设甲仓库原来运进货物x吨,则乙仓库运进货物(1260﹣x)吨,根据等量关系:甲仓库原来运进货物﹣120吨=乙仓库原来运进货物+120吨,列方程解答即可.
11.解:
3×2=6(人)
(108-6)÷2
=102÷2
=51(人)
51+6=57(人)
答:四(1)班有57人,四(2)班有51人。
【解析】从四(1)班转3人到四(2)班,则两班人数同样多,说明从四(1)班比四(2)班多6人;根据和差问题的解法解答,(和-差)÷2=小数,小数+差=大数。
12.解:(680+120)÷2
=800÷2
=400(元)
400-120=280(元)
答:上衣400元,裤子280元。
【解析】和差问题:(和+差)÷2=大数,大数-差=小数,据此解答。
13.解:4+1+1
=5+1
=6(只)
(20-6)÷2
=14÷2
=7(只)
7+6=13(只)
答:甲笼里原有小鸡7只,乙笼里原有小鸡13只。
【解析】甲、乙两个笼里小鸡相差的只数=4+1+1=6只,甲笼里原有小鸡的只数=(总只数-6只)÷2,乙笼里原有小鸡的只数=甲笼里原有小鸡的只数+6只。
14.解:(22-4)÷2
=18÷2
=9(只)
9+4=13(只)
答:小勇家养的白兔有9只,黑兔有13只。
【解析】小勇家养白兔的只数=(总只数-4只)÷2;养黑兔的只数=小勇家养白兔的只数+4只。
15.解:486÷3.6=135(千米/时)
(135+15)÷2
=150÷2
=75(千米/时)
答:乙车每小时行驶75千米。
【解析】路程÷相遇时间=甲、乙两车的速度和;甲、乙两车的速度差是15,按和差问题计算,(和+差)÷2=大数,据此解答。
16.解:(10+5+10)×7
=(15+10)×7
=25×7
=175(台)
答:一个星期商店卖出电脑和彩电一共175台。
【解析】一个星期商店卖出电脑和彩电的总台数=(平均每天卖出电脑的台数+平均每天卖出彩电的台数)×卖的天数;其中,平均每天卖出彩电的台数=平均每天卖出电脑的台数+5台。
17.(1)解:
(2)五年级植树的棵数;六年级植树的棵数
【解析】解:(2)列式(108-22)÷2,求的是五年级植树的棵数;
列式(108+22)÷2,求的是六年级植树的棵数。
故答案为:(2)五年级植树的棵数;六年级植树的棵数。
【分析】(1)五、六年级共植树 108 棵,六年级比五年级多植 22 棵,把这两个条件填在小括号里面;
(2)已知两个数的和与两个数的差,可以用和差问题解决:(和+差)÷2=较大数,(和-差)÷2=较小数。
18.解:(2100+1600)÷2
=3700÷2
=1850(克)
答:苹果的质量为1850克。
【解析】(和+差)÷2=较大数,和-较大数=较小数。
19.解:14-8=6(岁)
(42-6)÷2
=36÷2
=18(岁)
18+6=24(岁)
答:那时哥哥24岁,妹妹18岁。
【解析】无论过去几年,两个人的年龄差不变,那时妹妹的年龄=(总岁数-6岁)÷2,哥哥的年龄=妹妹的年龄+6岁。
20.解:48-42=6(分)
(44+6)÷2
=50÷2
=25(分)
答:妹妹做英语练习用了25分钟。
【解析】“姐姐做自然练习比妹妹做算术练习多用48分钟,比妹妹做英语练习多用42分钟”,由此可以推出妹妹做算术练习比做英语练习少用时间:48-42=6分钟,则妹妹做英语练习的时间=(妹妹做算术、英语两门练习共用的时间+6分钟)÷2。
21.解:9-2=7(本)
(47-7)÷2
=40÷2
=20(本)
20+9=29(本)
20+7=27(本)
答:甲有29本,乙有20本,丙有27本。
【解析】甲的书比乙多9本,比丙多2本,说明乙的书比丙少9-2=7本,乙有书的本数=(乙、丙共有书的本数-7本)÷2,甲有书的本数=乙有书的本数+9本,丙有书的本数=乙有书的本数+7本。
22.解:小明徒步走的速度是 ,所以小明徒步上楼需 (秒)。
答:小明徒步沿扶梯上楼需16秒。
【解析】扶梯+小明走的速度和=1÷12=,小明走的速度-扶梯的速度差为:1÷24=,两个小明走的速度和为:+=,小明的速度:÷2=,时间=1÷=16(秒)
【分析】和差问题,大数+小数=和,大数-小数=差,(和+差)÷2=大数,(和-差)÷2=小数
23.解:(720-160)÷2
=560÷2
=280(本)
280+160=440(本)
答:科技书有280本,故事书有440本。
【解析】科技书的本数=(总本数-故事书比科技书多的本数)÷2;故事书的本数=科技书的本数+160本。
24.解:乙箱原有水果:
(60﹣5×2)÷2
=50÷2
=25(千克),
答:乙箱有水果25千克.
【解析】由“从甲箱中取出5千克放入乙箱,两箱水果就一样重”,可知甲箱比乙箱原来重5×2=10(千克),然后根据和差问题的解法,解答即可.
25.解:(425-75)÷2=175(棵)
答:桃树有175棵。
【解析】本题已知桃树和梨树的和与差,采取和差公式,桃树(小数)=(和-差)÷2;梨树(大数)=(和+差)÷2;据此代入数值计算即可。
26.解:10-4=6(本)
(66-6)÷2
=60÷2
=30(本)
30+6=36(本)
答:甲箱原有图书36本、乙箱原有图书30本。
【解析】甲箱如果借出10本,就比乙箱少4本,则说明原来甲箱比乙箱多10-4=6本,乙箱原有图书的本数=(总本数-6本)÷2、甲箱原有图书的本数=乙箱原有图书的本数+6本。
27.解:长方形的周长:680÷4=170(米)
长方形长宽的和:170÷2=85(米)
(85+15)÷2=100÷2=50(米)
50-15=35(米)
答:操场的长是50米,宽是35米。
【解析】和差问题:(和+差)÷2=较大数,和-较大数=较小数。
28.解:画图分析:
27÷3=9(只) 9+2=11(只) 9-2=7(只) 答:白兔有9只,黑兔有11只,灰兔有7只。
【解析】黑兔比白兔多2只,灰兔比白免少2只,把黑兔比白兔多的补到灰兔比白免少的部分,这样黑兔、白兔、灰兔共27只也可以看成是3倍白兔这么多,因此可以先求出白兔的只数=27÷3=9只,黑兔的只数=白兔的只数+2只,灰兔的只数=白兔的只数-2只。
29.150×2÷20=15(cm)
答:BC长15厘米。
【解析】 涂色部分甲的面积比涂色部分乙的面积大 如果甲加上一个空白部分,乙也加一个相同的空白部分,就是半圆的面积比三角形面积大7平方厘米。已知圆的半径可以求出半圆的面积,继而求出三角形的面积,而三角形的高是圆的直径,所以可以求出三角形底边BC的长度。
30.解:今年两人的年龄之和:18+3+3=24(岁)
弟弟的年龄:(24+4) ÷2=14(岁)
答:哥哥今年14岁。
【解析】用两人三年前的年龄之和加上两个3即可求出今年两人的年龄。如果把弟弟的年龄加上4就和哥哥同样多,所以用两人的年龄和加上4,再除以2即可求出哥哥今年的年龄。
31.解:4+4+4
=8+4
=12
(105-12)÷3
=93÷3
=31
答:丙数是31。
【解析】已知甲数比乙数多4,乙数比丙数多4,可求出甲数比丙数多4+4=8;如果甲数少8,乙数少4,则甲、乙、丙三数相等,差正好是丙的3倍,除以3便可求出丙数。
32.解:
7+7=14(张)
(94-14)÷2=40(张)
94-40=54(张)
答:小明原来有40张邮票,小青原来有54张邮票。
【解析】小青给小明7张后,两人邮票的张数同样多,说明小青原来比小明多2个7张,那么小明原来有邮票的张数=(他们一共有邮票的张数-多的张数)÷2,小青原来有邮票的张数=他们一共有邮票的张数-小明原来有邮票的张数,据此代入数值作答即可。
33.解:由题目条件,甲班捐书最多,丙班最小,甲班比丙班多捐28+101=129(册);
又各班捐书总数都在400册与550册之间,则丙班捐书不少于400册,所以甲班捐书在529~550册之间;
设甲班有x人,乙班有y人,丙班有z人,则甲班共捐书(6+2×7+11×(x-3))册,乙班共捐书(6+3×8+10×(y-4))册,丙班共捐书(2×4+6×7+9×(z-8))册;
依题意,有
解之,得
答:甲班有51人,乙班有53人,丙班有49人。
【解析】本题考查了三元一次方程组的应用,解题的关键是:甲班比丙班多捐28+101=129(册)。根据题意,甲班捐书最多,丙班最小,甲班比丙班多捐28+101=129(册);又各班捐书总数都在400册与550册之间,则丙班捐书不少于400册,所以甲班捐书在529~550册之间。
34.解:48÷2=24(人)
12÷2=6(人)
24+6=30(人)
答:甲校有30人转入乙校。
【解析】根据“甲校原来比乙校多48人”可知甲校转入24人到乙校时,两所学校的人数一样。当甲校继续有同学转入到乙校时,每转入一个同学,甲校就比乙校少2人。当再从甲校转入6人到乙校时,甲校就比乙校少12人,所以甲校一共转入乙校 (人)时,甲校就比乙校少12人。
35.解:9-5=4(千克)
(24-4)÷2
=20÷2
=10(千克)
10+4=14(千克)
答:原来小油桶装油10千克,大油桶装油14千克。
【解析】两个油桶都倒出同样多的油后分别还剩9千克和5千克,那么也就是说大桶比小桶多4千克的油;原来小油桶装油的质量=(总质量-4千克)÷2,大油桶装油的质量=小油桶装油的质量+4千克。
36.解:设第一堆苹果原来有x个,则第二堆有(x+3)个,第三堆有(x+1)个,第四堆有2(x+1)个。
x+x+3+(x+1)+2(x+1)=46
4x+5=46
x=40÷4
x=9
第二堆:9+3=12(个);
第三堆:×(9+1)=5(个);
第四堆:2×(9+1)=20(个)。
答:这四堆苹果原来各有9个,12个,5个,20个。
【解析】分析题意可得:第一堆原有苹果数+1=第二堆原有苹果数-2,则第二堆原有苹果数=第一堆原有苹果数+1+2=第一堆原有苹果数+3;第一堆原有苹果数+1=第三堆原有苹果数×2,则第三堆原有苹果数=(第一堆原有苹果数+1)×;第一堆原有苹果数+1=第四堆原有苹果数×,则第四堆原有苹果数=(第一堆原有苹果数+1)×2;
第一堆原有苹果数+(第一堆原有苹果数+3)+(第一堆原有苹果数+1)×+(第一堆原有苹果数+1)×2=四堆苹果总数,据此关系式设第一堆苹果原来有x个,则第二堆有(x+3)个,第三堆有(x+1)个,第四堆有2(x+1)个,列方程即可解答。
37.解:(32+22+30)÷2
=(54+30)÷2
=84÷2
=42(元)
丙:42-32=10(元)
甲:42-30=12(元)
乙:42-22=20(元)
答:甲、乙、丙各储蓄12元、20元、10元。
【解析】甲储蓄的钱数=三人储蓄的钱数和-乙丙共储蓄的钱数、乙储蓄的钱数=三人储蓄的钱数和-甲丙共储蓄的钱数、丙储蓄的钱数=三人储蓄的钱数和-甲乙共储蓄的钱数;其中,三人储蓄的钱数和=(乙丙共储蓄的钱数+甲丙共储蓄的钱数+甲乙共储蓄的钱数)÷2。
38.解:
苹果 (164﹣3×3﹣5×4)÷(2+3+4)
=(164﹣9﹣20)÷9
=135÷9
=15(千克)
梨 15+3=18(千克)
桃子15+5=20(千克)
答:苹果每箱重15千克、梨每箱重18千克、桃子每箱重20千克.
【解析】根据“水果店运来每箱苹果比梨轻3千克,每箱桃子比苹果重5千克”,可知梨和桃子每箱都比苹果重,假设运来的都是苹果,则从总质量164千克里去 掉3箱梨比3箱苹果多的和4箱桃子比4箱苹果多的质量,用假设的苹果总质量除以假设的苹果总箱数,求出每箱苹果的质量,进而求出梨和桃子每箱的质量.
39.解:(78-6)÷2
=72÷2
=36(张)
36+6=42(张)
答:小红36张,小军42张。
【解析】小红集邮的张数=(两人集邮的总张数-6张)÷2;小军集邮的张数=小红集邮的张数+6张。
40.解:[78﹣(16+2)]÷2
=[78﹣18]÷2
=60÷2
=30(个)
78﹣30=48(个)
答:体育场原有篮球30个,足球48个。
【解析】借给四(1)班2个足球后,足球仍比篮球多16个,可知体育场原有足球比篮球多16+2=18(个),用总数78减18再除以2即可得篮球的个数,再求足球个数即可。
41.解:20×2+10
=40+10
=50(人)
(1050-50)÷2
=1000÷2
=500(人)
500+50=550(人)
答:乙校原来有学生500人,甲校原来有学生550人。
【解析】乙校原来有学生的人数=(总人数-由甲校转入乙校的人数×2-10人)÷2,甲校原来有学生的人数=乙校原来有学生的人数+50人。
42.解:根据题意得:
将①-②×2得:b=2-3c③,
将③代入②中得:a=2+4c ,
S= 2a +b-2c=2(2+4c)+2-3c-2c =6+3c;
因为a、b、c是非负数,所以0≤c≤,0≤2-3c,
由于S=6+3c,可知,S随c的增大而增大,
当c=0时,S=6+3c=6,
当c=时,S=6+3c=6+3×=10.5,
则S的最大值与最小值之差是10.5-6=4.5。
答:S的最大值与最小值之差是4.5
【解析】根据题意建立方程组,加减消元法得到用c表示b的代数式,再代入方程组可以得到用c表示a的代数式,化简 S=2a+b-2c=6+3c,因为a、b、c是非负数,可以得到c的范围,根据S随c的增大而增大,可得S的最大值与最小值,即可解答。
43.解:15-10=5(岁)
(49+5)÷2
=54÷2
=27(岁)
(49-5)÷2
=44÷2
=22(岁)
答:当两人的年龄和为49岁时,小明22岁,小强27岁。
【解析】本题可先求出两人的年龄差,又已知两人的年龄和,这道题就变为一道“和差”问题。
44.解:四年级:
(160+20)÷2
=180÷2
=90(人)
三年级:
160﹣90=70(人)
答:三年级有70人,四年级有90人。
【解析】假如把三年级的人数加上20人,那么两个年级的人数就相等,总人数也会增加20人,因此用增加后的总人数除以2即可求出四年级的人数,进而求出三年级的人数即可。
45.解:
146÷2=73(张)
73+23=96(张)
73-23=50(张)
答:王婷原有画片96张,李红原有画片50张。
【解析】两人同样多时的张数=画片的总数÷2,王婷原有画片是张数=同样多时的张数+王婷给李红的张数,李红原有画片是张数=同样多时的张数-王婷给李红的张数。
46.解:525÷5=105(元)
(105+15)÷2=60(元)
60-15=45(元)
答:足球的单价是60元,排球的单价是45元。
【解析】此题属于和差问题:一个足球和一个排球的差是15元;
5个足球和5个排球一共用去525元,据此求出一个足球和一个排球的和;
(和+差)÷2=大数,大数-差=小数,据此解答。
47.解:126-30=96(只)
鸭:96÷2=48(只)
鸡:126-48=78(只)
答:饲养场原来养鸭48只,养鸡78只。
【解析】分析题意可知:鸡、鸭总数减去30只鸡后,鸡、鸭只数相等,所以,(鸡、鸭总数-30)÷2=鸭的只数,鸡、鸭总数-鸭的只数=鸡的只数。
48.解:4-3+2
=1+2
=3(枝)
(25-3)÷2
=22÷2
=11(枝)
11+3=14(枝)
答:小敏原来有11枝铅笔,小华原来有14枝铅笔。
【解析】如果小华用去4枝,小敏用去3枝,那么小华还比小敏多2枝,这就说明原来小华的铅笔比小敏的铅笔多3枝;小敏原来有铅笔的枝数=(总枝数-3枝)÷2,小华原来有铅笔的枝数=小敏原来有铅笔的枝数+3枝。
49.甲队原有人数:(285×2+24+1980)÷2=1287(人)
乙队原有人数:1287-594=693(人)
答:甲队原有1287人,乙队原有693人。
【解析】根据 “ 甲、乙两个工程队共1980人, ”可知甲、乙两个工程队人数和为1980人,甲队抽出285人调入乙队,这时乙队人数还比甲队少24人 ,可知甲队和乙队人数差是285×2+24=594人,所以根据和差公式,“(和+差) ÷2=大数,大数-差=小数”的公式,即可求出两队原有的人数。
50.解:(68-20)÷2
=48÷2
=24(只)
24+20=44(只)
答:她家原来养鸭20只,养鸡44只。
【解析】把卖掉的减去后,鸡的只数和鸭的只数相同,除以2就是鸭的只数;鸭的只数加上20只,就是鸡的只数。
21世纪教育网(www.21cnjy.com)
同课章节目录
