【期末押题卷】期末模拟高频易错预测卷(含解析)-2024-2025学年人教版数学六年级下册
文档属性
| 名称 | 【期末押题卷】期末模拟高频易错预测卷(含解析)-2024-2025学年人教版数学六年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 279.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末模拟高频易错预测卷
2024-2025学年人教版数学六年级下册
一、选择题
1.在计算2.4×时,( )来计算比较简便。
A.化作分数 B.直接约分再算 C.化作小数
2.一个半圆,它的半径是r,这个半圆的周长是多少?( )
A. B. C. D.
3.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量。( )
A.成正比例 B.成反比例 C.不成比例
4.下面直线上,点M表示的数是( )。
A. B. C. D.1.2
5.一台电冰箱的原价是2400元,现在按八折出售,求现价多少元?列式是( )。
A.2400÷80% B.2400×80% C.2400×(1-80%)
6.甲数是乙数的80%,若甲数是40,那么乙数是( )
A.80 B.3200 C.60 D.50
7.一桶油重1千克,倒出后,又灌进千克,这时油桶的油( )。
A.和原来一样多 B.比原来少 C.比原来多
8.配制一种药水,药粉和水的质量比是1:40,要配制205千克的药水,需要药粉( ).
A.5千克 B.10千克 C.20千克
9.一件工作,甲单独做用的时间比乙单独做多,甲和乙工作效率的比是( )
A.1∶1 B.3∶4 C.4∶3 D.5∶3
二、填空题
10.武汉某一天的最高气温是零上6℃,记作﹢6℃,最低气温是零下3℃,记作( ),这一天的温差是( )℃。
11.一种压路机滚筒是一个圆柱体,它的底面直径是1m,长是2m。如果它转1圈,压路机前进了( )m,一共压路( )m2。
12.一辆汽车行7.5千米需要汽油升,那么用1升汽油可行 千米.
13.的是 , 的 是 .
14.乙数的等于甲数,甲数是32,乙数是 .
15.把一根4米长的圆柱形木条锯成三段,表面积增加了12平方分米,这根圆柱形木条每段的体积是 立方米.
16.小明和小林是两个集邮爱好者,他们共有邮票400多张,如果小明给小林a张邮票,小明就比小林少;如果小林给小明a张邮票,则小林就比小明少.那么小明原有 张邮票,小林原有 张邮票.
三、判断题
17.千克=62.5%千克。( )
18.1吨煤用去一半,还剩50%吨。( )
19.利息和利率是一回事。( )
20.李大伯一次种了101棵树,成活了99棵,李大伯这次种树的成活率是99%. ( )
21.两根一样长的绳子,第一根用去,第二根用去米,余下的长度相等。( )
22.吨花生可以榨油吨,表示1吨花生可榨油多少吨。( )
23.因为,所以。( )
四、计算题
24.化简比。
14∶21 26∶39 ∶ 1∶ 0.5∶2.5 0.75∶
25.计算。
15×36+368÷23 35-1.8÷0.9×2.5
26.看图列式计算。
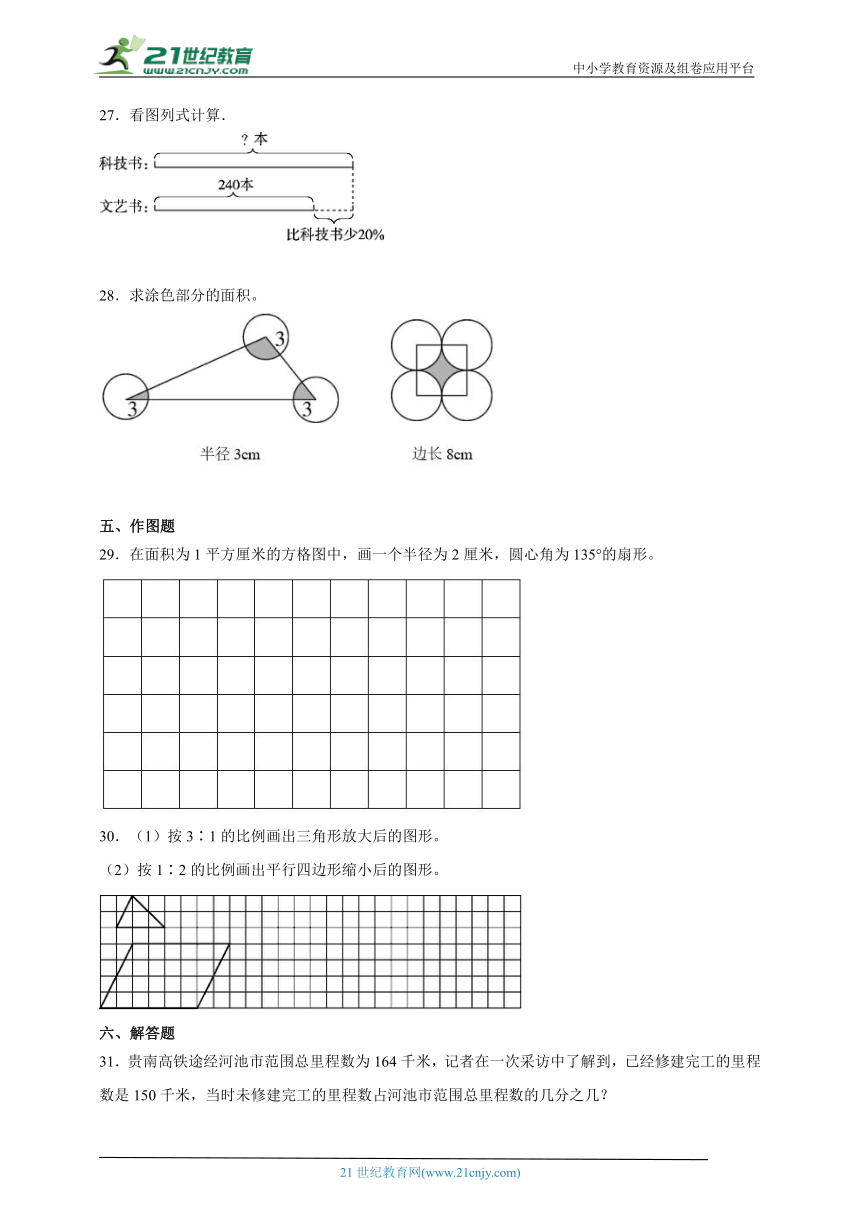
27.看图列式计算.
28.求涂色部分的面积。
五、作图题
29.在面积为1平方厘米的方格图中,画一个半径为2厘米,圆心角为135°的扇形。
30.(1)按3∶1的比例画出三角形放大后的图形。
(2)按1∶2的比例画出平行四边形缩小后的图形。
六、解答题
31.贵南高铁途经河池市范围总里程数为164千米,记者在一次采访中了解到,已经修建完工的里程数是150千米,当时未修建完工的里程数占河池市范围总里程数的几分之几?
32.乘坐公交车如果刷卡每人每次需支付1.6元,比投币便宜了,投币支付每人每次需多少元?
33.小明的爷爷今年75,爸爸的年龄是爷爷的,小明的年龄是爸爸的。小明今年多少岁?
34.六年级的同学给灾区的小朋友捐款,一班捐了650元,二班捐的是一班的,二班捐款多少元?
35.榨油厂的王师傅用400kg油菜籽榨出菜籽油168kg。这批油菜籽的出油率是多少?
36.在一个底面半径为10厘米的圆柱形杯里装满水,水里放了一个底面半径为5厘米的圆锥形铅锤,当铅锤从水中完全取出后,杯里的水面下降了0.5厘米,这个铅锤的体积是多少?
37.乐乐读一本数学家的故事书,共120页,第一天读了全书的20%,第一天比第二天少读4%,第二天读了多少页?
38.一批商品按期望获得50%的利润定价,结果只卖掉70%的商品,为尽早卖出余下商品,决定打折出售,这样获得的全部利润是原来期望利润的82%,余下部分商品商店是打几折出售的?
答案与解析
1.B
【解题思路】根据分数与小数乘法的计算法则:分数的分母与小数能约分的先约分,再计算;如果不能约分,把小数转换成分数,按分数乘分数的方法进行计算。
【精讲精析】
在计算2.4×时,直接约分再算比较简便。
故答案为:B
【要点提示】掌握分数与小数乘法的计算法则是解题的关键。
2.C
【解题思路】周长是指封闭图形一周的长度。半圆的周长等于该圆周长的一半加上一条直径的长度,根据圆的周长公式C=,圆的直径d=2r,据此解答。
【精讲精析】
=
=
即这个半圆的周长是。
故答案为:C
【要点提示】明确半圆的周长由哪几部分组成是解答本题的关键。
3.B
【解题思路】根据数量关系判断麻袋的数量和每袋化肥重量的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例。
【精讲精析】麻袋的数量×每袋化肥的重量=这堆化肥的总重量,总重量不变,麻袋的数量和每袋化肥的重量成反比例。
故答案为:B
4.C
【解题思路】从图片中观察得出,M在﹣1到0之间,则M是负数,排除正数的选项,且M点靠近﹣1,得出M点代表的数是。
【精讲精析】根据分析,点M在-1和0之间,直线上点M表示的数应是。
故答案为:C
5.B
【解题思路】八折出售的意思就是现价是原价的80%,以原价为单位“1”,用原价乘80%即可求出现价。
【精讲精析】根据数量关系列式为:2400×80%。
故答案为:B
【要点提示】在日常生活中,折扣是较为常见的现象,要准确理解其含义,运用百分数运算求得结果。
6.D
【解题思路】把乙数看作单位“1”,根据已知一个数的几分之几是多少,求这个数,用除法进行解答即可。
【精讲精析】40÷80%=50
故答案为:D
【要点提示】解答此题的关键是:先判断出单位“1”,进而根据“对应数÷对应分率=单位“1”的量”进行解答即可。
7.A
【解题思路】一桶油重1千克,倒出 后,则还剩下全部的1-,根据分数乘法的意义可知,还剩下1×(1- )千克,再灌进千克,此时桶内有1×(1-)+千克。
【精讲精析】1×(1-)+
=1×+
=+
=1(千克)
即这时桶内的油和原来一样多。
故答案为:A。
【要点提示】完成本题要注意前后两个分数的不同,前一个表示占总数的分率,后一个表示具体数量。
8.A
9.B
【解题思路】根据甲单独做用的时间比乙单独做多,把乙单独做用的时间看做单位“1”,甲单独做用的时间比乙单独多,即甲单独做用的时间是乙单独的(1+),把总工作量看做整体1,由工作效率,工作时间,工作总量三者的关系即可以解答。
【精讲精析】1÷(1+)
=1÷
=
所以甲和乙工作效率的比是3∶4
【要点提示】此题先找准单位“1”,再根据工作效率=工作总量÷工作时间,即可以解答。
10. ﹣3℃ 9
【解题思路】正负数表示一组相反意义的量,此题中零上和零下就是一组相反意义的量,零上记作正,零下就记作负,据此解答即可;用最高气温减去最低气温即可求出相差的温度。
【精讲精析】零上6℃,记作﹢6℃,最低气温是零下3℃,记作﹣3℃;
6-(﹣3)=9℃
【要点提示】明确正负数的意义是解答本题的关键。
11. 3.14 6.28
【解题思路】滚筒转动1圈前进了多少米是求圆柱的底面周长,压路机滚筒转动1圈压过的路面面积是求圆柱的侧面积。
【精讲精析】圆柱底面周长:3.14×1=3.14(m)
圆柱侧面积:3.14×2=6.28(m2)
所以滚筒转动1圈,压路机前进了3.14m,一共压路6.28m2。
12.12.5.
【精讲精析】试题分析:用行驶的路程除以汽油的升数,就是1升汽油可行驶的路程.
解:7.5=12.5(千米);
答:用1升汽油可行12.5千米.
故答案为12.5.
点评:本题中汽油的量是单一的量,就把行驶的路程进行平均分即可.
13.
【解题思路】根据一个数乘分数的意义就表示求这个数的书几分之几是多少,所以求 的 是多少用乘法计算;根据已知一个数的几分之几是多少,求这个数用除法计算,所以第二问用 除以计算.
【精讲精析】解:x=
÷=
答; 的 是, 的是 .
14.36
【精讲精析】试题分析:把乙数看成单位“1”,它的对应的数量是32,由此用除法求出乙数.
解:32÷=36;
答:乙数是36.
故答案为36.
点评:本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法.
15.0.04.
【精讲精析】试题分析:首先根据锯木问题,锯的段数比锯的次数多1,锯成3段需要锯2次,每锯1次就增加两个截面,那么锯两次就增加4个截面.已知表面积增加了12平方分米,表面积增加的计算4个截面的面积和,所以每个截面的面积是12÷4=3平方分米,根据圆柱的体积公式:v=sh,把数据代入公式解答.
解:
圆柱的底面积:
12÷4=3(平方分米),
3平方分米=0.03平方米,
每段的体积:
0.03×4÷3,
=0.12÷3,
=0.04(立方米);
答:这根圆柱形木条每段的体积是0.04立方米.
故答案为0.04.
点评:此题解答关键是理解把圆柱形木条锯成3段表面积增加的是4个截面的面积,它的侧面积不变,由此求出每个截面的面积,再根据圆柱的体积公式解答,注意在计算体积时底面积和高必须使用对应单位.
16.227,221.
【精讲精析】试题分析:因为小明给小林a张邮票,小明就比小林少;把小林的邮票的张数看作单位“1”,表示出总张数与小林的邮票的张数的比1﹣+1=,同理,把小明的邮票的张数看作单位“1”,小林给小明a张邮票,则小林就比小明少,邮票的总张数与小明的邮票张数的比是1﹣+1=,然后找出32与28的公倍数,至少224张,因为总数是400多张,由此求出邮票的总张数,224×2=448张,进一步求出各自的张数.
解:1﹣+1=,
1﹣+1=,
总数是32与28的公倍数,至少224张
又已知总数在400多,
所以总数为224×2=448(张),
448÷=266(张),
448÷×(1﹣)=176(张),
小林原有:(266+176)÷2=221(张);
小明原有:448﹣221=227(张);
点评:本题运用题目中的条件,选用求最小公倍数的方法求出总张数,即可求得各自的张数.
17.×
【解题思路】百分数是“表示一个数是另一个数百分之几的数。”它只能表示两数之间的倍数关系,不能表示某一具体数量,所以,千克=62.5%千克的表示方法是错误的。
【精讲精析】根据百分数的意义可知,百分数不能表示某一具体数量,所以,千克=62.5%千克的表示方法是错误的。
故答案为:×
【要点提示】百分数不能表示具体的数量是百分数与分数的区别之一。
18.×
【解题思路】我们求出还剩下多少千克,用不同的数进行表示,进一步说明用百分数不能表示具体的数量。即百分数的后面不能带单位。
【精讲精析】1×(1-)
=1×
=0.5(吨)
0.5吨=吨,但不能表示成50%吨,百分数不能表示具体的数量,只能表示数的百分比。所以题干中的说法是错误的。
故答案为:×
【要点提示】本题考查了关于百分数的问题,百分数不能表示具体的数量。
19.×
【解题思路】根据利息=本金×利率×存期,可知利息是从银行里能取出来的多余的钱,利率是银行支付给存款人定期存款额的报酬率,二者不相同。
【精讲精析】由分析知,利息和利率不是一回事。例如:本金是3000元,利率是3.75%,存期3年,则利息是:3000×3.75%×3
=112.5×3
=337.5(元)
二者不相同,所以原题干说法错误。
故答案为:×
【要点提示】本题考查了存款利息相关问题,明确利率是个百分率,而利息是个具体的数量。
20.错误
【解题思路】成活率=×100%
【精讲精析】99÷101×100%≈0.98×100%=98%
故答案为错误
21.×
【解题思路】和米是无法比较的,是一个分率,没有单位,米有单位,是一个具体的量,也可以假设具体的长度来判断。
【精讲精析】假设两根绳子都长2米,那第一根剩下1米,第二根剩下的是1.5米;两根绳子都长1米,那第一根剩下0.5米,第二根剩下的也是0.5米,则余下的长度相等;两根绳子都长0.8米,那第一根剩下0.4米,第二根剩下的是0.3米,则剩下的长度不一样。
故判断错误。
【要点提示】要注意分数带单位和不带单位的区别,一个量不确定,它的几分之几具体是多少我们也是无法直接判断是多少的。
22.√
【解题思路】除数表示哪种量,式子就是求哪种单一的量。吨表示花生的质量,则表示1吨花生可榨油多少吨。
【精讲精析】通过分析可得:是用油的质量除以对应的花生的质量,表示1吨花生可榨油多少吨。原题说法正确。
故答案为:√
23.×
【解题思路】(1) 当A、B不为零时,首先根据:分子相同,则分母小的分数大,判断出、的大小关系;然后根据:两个非零因数的乘积一-定时,其中的一个因数越大,则另一个因数越小,判断出A、B的大小关系即可.
(2)当A=B=0时,也成立。
【精讲精析】(1)让,
则,,
所以,,
(2)当时,
,
故本题说法错误。
【要点提示】解答本题的关键是:要考虑A和B的特殊值,做出相应的判断。
24.2∶3;2∶3;22∶5;5∶4;1∶5;6∶1
【解题思路】(1)整数比的化简方法:比的前项和后项同时除以它们的最大公因数;
(2)小数比的化简方法:先根据比的基本性质移动小数点的位置,把小数比化为整数比,再按照整数比的化简方法计算;
(3)分数比的化简方法:比的前项和后项同时乘分母的最小公倍数,把分数比化为整数比,再按照整数比的化简方法计算;据此解答。
【精讲精析】(1)14∶21=(14÷7)∶(21÷7)=2∶3
(2)26∶39=(26÷13)∶(39÷13)=2∶3
(3)∶=(×24)∶(×24)=22∶5
(4)1∶=(1×5)∶(×5)=5∶4
(5)0.5∶2.5=(0.5×10)∶(2.5×10)=5∶25=(5÷5)∶(25÷5)=1∶5
(6)0.75∶=∶=(×8)∶(×8)=6∶1
25.556;30;
;80
【解题思路】(1)按照运算顺序,先算乘除法,再算加法;
(2)按照运算顺序,先算除法,再算乘法,最后算减法;
(3)按照运算顺序,有括号先算括号里的除法,再算括号里的加法,最后算括号外面的乘法;
(4)按照运算顺序,先算小括号的减法,再算中括号里的乘法,最后算括号外面的除法。
【精讲精析】(1)15×36+368÷23
(2) 35-1.8÷0.9×2.5
(3)
(4)
26.420÷=980(千克)
【解题思路】看图可知,所求千克数是单位“1”,已知千克数是所求千克数的,已知千克数÷对应分率=所求千克数,据此列式计算。
【精讲精析】420÷=420×=980(千克)
27.240÷(1-20%)
28.14.13cm2; 13.76cm2
【解题思路】通过图可知,由于三角形的内角和是180°,所以第一个图形的三个扇形拼接在一起正好能够构成一个半径是3厘米的半圆,根据半圆的面积公式:S=πr2÷2,把数代入即可求解;
通过图可知,两个半径构成一个正方形边长,即圆的半径:8÷2=4厘米,正方形里面相当于4个的圆,那拼在一起相当于一个半径是4厘米的圆,用正方形的面积-4个圆的面积=涂色部分面积;根据正方形的面积公式:边长×边长,圆的面积公式:S=πr2,把数代入即可求解。
【精讲精析】第一个图形:3.14×32÷2
=3.14×9÷2
=28.26÷2
=14.13(cm2)
第二个图形:8×8-3.14×(8÷2)2
=64-3.14×42
=64-3.14×16
=64-50.24
=13.76(cm2)
29.【解题思路】把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。在圆内以一条半径为边,画一个130°的角,两个半径和圆弧围起来的部分就是扇形。
【精讲精析】作图如下:
【要点提示】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。扇形是圆的一部分。
30.【精讲精析】如图:
31.
【解题思路】根据题意,当时未修建完工的里程数是(164-150)千米,已知贵南高铁途经河池市范围总里程数为164千米,求当时未修建完工的里程数占河池市范围总里程数的几分之几,实际上是求一个数占另一个数的几分之几,用除法,用(164-150)除以164,即可得解。
【精讲精析】(164-150)÷164
=14÷164
=
答:当时未修建完工的里程数占河池市范围总里程数的。
【要点提示】此题的解题关键是掌握求一个数占另一个数的几分之几的计算方法。
32.2元
【解题思路】把投币支付每人每次需支付的钱数看作单位“1”,刷卡每人每次需支付的钱数相当于投币支付,根据分数除法的意义,用刷卡每人每次需支付的钱数除以,就是投币支付每人每次需要支付的钱数。
【精讲精析】
(元)
答:投币支付每人每次需2元。
【要点提示】此题是考查分数除法的意义及应用。已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率。
33.25岁
【解题思路】求小明今年多少岁.根据“已知量×对应的率”的方法来求问题。可以先求出爸爸的年龄,再求小明的年龄。
【精讲精析】75××
=50×
=25(岁)
答:小明今年25岁。
【要点提示】本题中存在两个单位“1”,第一个是爷爷的年龄、第二个是爸爸的年龄,单位“1”已知用乘法计算,只是要将单位“1”与分率相对应。
34.520元
【解题思路】把一班捐款的金额看作单位“1”,单位“1”已知,根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用一班捐款的金额乘即可求出二班捐款的金额。
【精讲精析】650×=520(元)
答:二班捐款520元。
【要点提示】此题的解题关键是理解分数乘法的意义,掌握求一个数的几分之几是多少的计算方法,从而解决问题。
35.42%
【解题思路】用菜籽油的质量除以油菜籽的质量,求出出油率。
【精讲精析】168÷400×100%=42%
答:这批油菜籽的出油率是42%。
【要点提示】本题考查了百分率的应用,明确出油率的计算方法是解题的关键。
36.157立方厘米
【解题思路】根据题意得出这个铅锤的体积等于下降的水的体积,下降的水的体积是底面半径为10厘米,高为0.5厘米圆柱的体积,根据圆柱的体积=底面积×高即可解答。
【精讲精析】铅锤的体积:
3.14×10×0.5
=3.14×100×0.5
=157(立方厘米)
答:这个铅锤的体积是157立方厘米。
【要点提示】本题考查圆柱的体积,关键是掌握铅锤的体积与下降的水的体积相等。
37.25页
【精讲精析】120×20%÷(1-4%)
=24÷96%
=25(页)
38.八折
【精讲精析】实际利润为:50%×82%=41%;
打折部分利润率为:(41%-50%×70%)÷(1-70%)
=6%÷30%
=20%;
余下部分商品的价格是原价的:(1+20%)÷(1+50%)
=120%÷150%
=80%;
80%即八折.
答:余下部分商品商店是打八折出售的.
【要点提示】本题考查了利润、利润率及折扣问题.要熟练掌握公式:利润=售价-进价;利润率=利润÷进价;折扣=折后的价格÷原价.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末模拟高频易错预测卷
2024-2025学年人教版数学六年级下册
一、选择题
1.在计算2.4×时,( )来计算比较简便。
A.化作分数 B.直接约分再算 C.化作小数
2.一个半圆,它的半径是r,这个半圆的周长是多少?( )
A. B. C. D.
3.把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量。( )
A.成正比例 B.成反比例 C.不成比例
4.下面直线上,点M表示的数是( )。
A. B. C. D.1.2
5.一台电冰箱的原价是2400元,现在按八折出售,求现价多少元?列式是( )。
A.2400÷80% B.2400×80% C.2400×(1-80%)
6.甲数是乙数的80%,若甲数是40,那么乙数是( )
A.80 B.3200 C.60 D.50
7.一桶油重1千克,倒出后,又灌进千克,这时油桶的油( )。
A.和原来一样多 B.比原来少 C.比原来多
8.配制一种药水,药粉和水的质量比是1:40,要配制205千克的药水,需要药粉( ).
A.5千克 B.10千克 C.20千克
9.一件工作,甲单独做用的时间比乙单独做多,甲和乙工作效率的比是( )
A.1∶1 B.3∶4 C.4∶3 D.5∶3
二、填空题
10.武汉某一天的最高气温是零上6℃,记作﹢6℃,最低气温是零下3℃,记作( ),这一天的温差是( )℃。
11.一种压路机滚筒是一个圆柱体,它的底面直径是1m,长是2m。如果它转1圈,压路机前进了( )m,一共压路( )m2。
12.一辆汽车行7.5千米需要汽油升,那么用1升汽油可行 千米.
13.的是 , 的 是 .
14.乙数的等于甲数,甲数是32,乙数是 .
15.把一根4米长的圆柱形木条锯成三段,表面积增加了12平方分米,这根圆柱形木条每段的体积是 立方米.
16.小明和小林是两个集邮爱好者,他们共有邮票400多张,如果小明给小林a张邮票,小明就比小林少;如果小林给小明a张邮票,则小林就比小明少.那么小明原有 张邮票,小林原有 张邮票.
三、判断题
17.千克=62.5%千克。( )
18.1吨煤用去一半,还剩50%吨。( )
19.利息和利率是一回事。( )
20.李大伯一次种了101棵树,成活了99棵,李大伯这次种树的成活率是99%. ( )
21.两根一样长的绳子,第一根用去,第二根用去米,余下的长度相等。( )
22.吨花生可以榨油吨,表示1吨花生可榨油多少吨。( )
23.因为,所以。( )
四、计算题
24.化简比。
14∶21 26∶39 ∶ 1∶ 0.5∶2.5 0.75∶
25.计算。
15×36+368÷23 35-1.8÷0.9×2.5
26.看图列式计算。
27.看图列式计算.
28.求涂色部分的面积。
五、作图题
29.在面积为1平方厘米的方格图中,画一个半径为2厘米,圆心角为135°的扇形。
30.(1)按3∶1的比例画出三角形放大后的图形。
(2)按1∶2的比例画出平行四边形缩小后的图形。
六、解答题
31.贵南高铁途经河池市范围总里程数为164千米,记者在一次采访中了解到,已经修建完工的里程数是150千米,当时未修建完工的里程数占河池市范围总里程数的几分之几?
32.乘坐公交车如果刷卡每人每次需支付1.6元,比投币便宜了,投币支付每人每次需多少元?
33.小明的爷爷今年75,爸爸的年龄是爷爷的,小明的年龄是爸爸的。小明今年多少岁?
34.六年级的同学给灾区的小朋友捐款,一班捐了650元,二班捐的是一班的,二班捐款多少元?
35.榨油厂的王师傅用400kg油菜籽榨出菜籽油168kg。这批油菜籽的出油率是多少?
36.在一个底面半径为10厘米的圆柱形杯里装满水,水里放了一个底面半径为5厘米的圆锥形铅锤,当铅锤从水中完全取出后,杯里的水面下降了0.5厘米,这个铅锤的体积是多少?
37.乐乐读一本数学家的故事书,共120页,第一天读了全书的20%,第一天比第二天少读4%,第二天读了多少页?
38.一批商品按期望获得50%的利润定价,结果只卖掉70%的商品,为尽早卖出余下商品,决定打折出售,这样获得的全部利润是原来期望利润的82%,余下部分商品商店是打几折出售的?
答案与解析
1.B
【解题思路】根据分数与小数乘法的计算法则:分数的分母与小数能约分的先约分,再计算;如果不能约分,把小数转换成分数,按分数乘分数的方法进行计算。
【精讲精析】
在计算2.4×时,直接约分再算比较简便。
故答案为:B
【要点提示】掌握分数与小数乘法的计算法则是解题的关键。
2.C
【解题思路】周长是指封闭图形一周的长度。半圆的周长等于该圆周长的一半加上一条直径的长度,根据圆的周长公式C=,圆的直径d=2r,据此解答。
【精讲精析】
=
=
即这个半圆的周长是。
故答案为:C
【要点提示】明确半圆的周长由哪几部分组成是解答本题的关键。
3.B
【解题思路】根据数量关系判断麻袋的数量和每袋化肥重量的乘积一定还是商一定,如果乘积一定就成反比例,如果商一定就成正比例,否则不成比例。
【精讲精析】麻袋的数量×每袋化肥的重量=这堆化肥的总重量,总重量不变,麻袋的数量和每袋化肥的重量成反比例。
故答案为:B
4.C
【解题思路】从图片中观察得出,M在﹣1到0之间,则M是负数,排除正数的选项,且M点靠近﹣1,得出M点代表的数是。
【精讲精析】根据分析,点M在-1和0之间,直线上点M表示的数应是。
故答案为:C
5.B
【解题思路】八折出售的意思就是现价是原价的80%,以原价为单位“1”,用原价乘80%即可求出现价。
【精讲精析】根据数量关系列式为:2400×80%。
故答案为:B
【要点提示】在日常生活中,折扣是较为常见的现象,要准确理解其含义,运用百分数运算求得结果。
6.D
【解题思路】把乙数看作单位“1”,根据已知一个数的几分之几是多少,求这个数,用除法进行解答即可。
【精讲精析】40÷80%=50
故答案为:D
【要点提示】解答此题的关键是:先判断出单位“1”,进而根据“对应数÷对应分率=单位“1”的量”进行解答即可。
7.A
【解题思路】一桶油重1千克,倒出 后,则还剩下全部的1-,根据分数乘法的意义可知,还剩下1×(1- )千克,再灌进千克,此时桶内有1×(1-)+千克。
【精讲精析】1×(1-)+
=1×+
=+
=1(千克)
即这时桶内的油和原来一样多。
故答案为:A。
【要点提示】完成本题要注意前后两个分数的不同,前一个表示占总数的分率,后一个表示具体数量。
8.A
9.B
【解题思路】根据甲单独做用的时间比乙单独做多,把乙单独做用的时间看做单位“1”,甲单独做用的时间比乙单独多,即甲单独做用的时间是乙单独的(1+),把总工作量看做整体1,由工作效率,工作时间,工作总量三者的关系即可以解答。
【精讲精析】1÷(1+)
=1÷
=
所以甲和乙工作效率的比是3∶4
【要点提示】此题先找准单位“1”,再根据工作效率=工作总量÷工作时间,即可以解答。
10. ﹣3℃ 9
【解题思路】正负数表示一组相反意义的量,此题中零上和零下就是一组相反意义的量,零上记作正,零下就记作负,据此解答即可;用最高气温减去最低气温即可求出相差的温度。
【精讲精析】零上6℃,记作﹢6℃,最低气温是零下3℃,记作﹣3℃;
6-(﹣3)=9℃
【要点提示】明确正负数的意义是解答本题的关键。
11. 3.14 6.28
【解题思路】滚筒转动1圈前进了多少米是求圆柱的底面周长,压路机滚筒转动1圈压过的路面面积是求圆柱的侧面积。
【精讲精析】圆柱底面周长:3.14×1=3.14(m)
圆柱侧面积:3.14×2=6.28(m2)
所以滚筒转动1圈,压路机前进了3.14m,一共压路6.28m2。
12.12.5.
【精讲精析】试题分析:用行驶的路程除以汽油的升数,就是1升汽油可行驶的路程.
解:7.5=12.5(千米);
答:用1升汽油可行12.5千米.
故答案为12.5.
点评:本题中汽油的量是单一的量,就把行驶的路程进行平均分即可.
13.
【解题思路】根据一个数乘分数的意义就表示求这个数的书几分之几是多少,所以求 的 是多少用乘法计算;根据已知一个数的几分之几是多少,求这个数用除法计算,所以第二问用 除以计算.
【精讲精析】解:x=
÷=
答; 的 是, 的是 .
14.36
【精讲精析】试题分析:把乙数看成单位“1”,它的对应的数量是32,由此用除法求出乙数.
解:32÷=36;
答:乙数是36.
故答案为36.
点评:本题先找出单位“1”,已知一个数的几分之几是多少,求这个数用除法.
15.0.04.
【精讲精析】试题分析:首先根据锯木问题,锯的段数比锯的次数多1,锯成3段需要锯2次,每锯1次就增加两个截面,那么锯两次就增加4个截面.已知表面积增加了12平方分米,表面积增加的计算4个截面的面积和,所以每个截面的面积是12÷4=3平方分米,根据圆柱的体积公式:v=sh,把数据代入公式解答.
解:
圆柱的底面积:
12÷4=3(平方分米),
3平方分米=0.03平方米,
每段的体积:
0.03×4÷3,
=0.12÷3,
=0.04(立方米);
答:这根圆柱形木条每段的体积是0.04立方米.
故答案为0.04.
点评:此题解答关键是理解把圆柱形木条锯成3段表面积增加的是4个截面的面积,它的侧面积不变,由此求出每个截面的面积,再根据圆柱的体积公式解答,注意在计算体积时底面积和高必须使用对应单位.
16.227,221.
【精讲精析】试题分析:因为小明给小林a张邮票,小明就比小林少;把小林的邮票的张数看作单位“1”,表示出总张数与小林的邮票的张数的比1﹣+1=,同理,把小明的邮票的张数看作单位“1”,小林给小明a张邮票,则小林就比小明少,邮票的总张数与小明的邮票张数的比是1﹣+1=,然后找出32与28的公倍数,至少224张,因为总数是400多张,由此求出邮票的总张数,224×2=448张,进一步求出各自的张数.
解:1﹣+1=,
1﹣+1=,
总数是32与28的公倍数,至少224张
又已知总数在400多,
所以总数为224×2=448(张),
448÷=266(张),
448÷×(1﹣)=176(张),
小林原有:(266+176)÷2=221(张);
小明原有:448﹣221=227(张);
点评:本题运用题目中的条件,选用求最小公倍数的方法求出总张数,即可求得各自的张数.
17.×
【解题思路】百分数是“表示一个数是另一个数百分之几的数。”它只能表示两数之间的倍数关系,不能表示某一具体数量,所以,千克=62.5%千克的表示方法是错误的。
【精讲精析】根据百分数的意义可知,百分数不能表示某一具体数量,所以,千克=62.5%千克的表示方法是错误的。
故答案为:×
【要点提示】百分数不能表示具体的数量是百分数与分数的区别之一。
18.×
【解题思路】我们求出还剩下多少千克,用不同的数进行表示,进一步说明用百分数不能表示具体的数量。即百分数的后面不能带单位。
【精讲精析】1×(1-)
=1×
=0.5(吨)
0.5吨=吨,但不能表示成50%吨,百分数不能表示具体的数量,只能表示数的百分比。所以题干中的说法是错误的。
故答案为:×
【要点提示】本题考查了关于百分数的问题,百分数不能表示具体的数量。
19.×
【解题思路】根据利息=本金×利率×存期,可知利息是从银行里能取出来的多余的钱,利率是银行支付给存款人定期存款额的报酬率,二者不相同。
【精讲精析】由分析知,利息和利率不是一回事。例如:本金是3000元,利率是3.75%,存期3年,则利息是:3000×3.75%×3
=112.5×3
=337.5(元)
二者不相同,所以原题干说法错误。
故答案为:×
【要点提示】本题考查了存款利息相关问题,明确利率是个百分率,而利息是个具体的数量。
20.错误
【解题思路】成活率=×100%
【精讲精析】99÷101×100%≈0.98×100%=98%
故答案为错误
21.×
【解题思路】和米是无法比较的,是一个分率,没有单位,米有单位,是一个具体的量,也可以假设具体的长度来判断。
【精讲精析】假设两根绳子都长2米,那第一根剩下1米,第二根剩下的是1.5米;两根绳子都长1米,那第一根剩下0.5米,第二根剩下的也是0.5米,则余下的长度相等;两根绳子都长0.8米,那第一根剩下0.4米,第二根剩下的是0.3米,则剩下的长度不一样。
故判断错误。
【要点提示】要注意分数带单位和不带单位的区别,一个量不确定,它的几分之几具体是多少我们也是无法直接判断是多少的。
22.√
【解题思路】除数表示哪种量,式子就是求哪种单一的量。吨表示花生的质量,则表示1吨花生可榨油多少吨。
【精讲精析】通过分析可得:是用油的质量除以对应的花生的质量,表示1吨花生可榨油多少吨。原题说法正确。
故答案为:√
23.×
【解题思路】(1) 当A、B不为零时,首先根据:分子相同,则分母小的分数大,判断出、的大小关系;然后根据:两个非零因数的乘积一-定时,其中的一个因数越大,则另一个因数越小,判断出A、B的大小关系即可.
(2)当A=B=0时,也成立。
【精讲精析】(1)让,
则,,
所以,,
(2)当时,
,
故本题说法错误。
【要点提示】解答本题的关键是:要考虑A和B的特殊值,做出相应的判断。
24.2∶3;2∶3;22∶5;5∶4;1∶5;6∶1
【解题思路】(1)整数比的化简方法:比的前项和后项同时除以它们的最大公因数;
(2)小数比的化简方法:先根据比的基本性质移动小数点的位置,把小数比化为整数比,再按照整数比的化简方法计算;
(3)分数比的化简方法:比的前项和后项同时乘分母的最小公倍数,把分数比化为整数比,再按照整数比的化简方法计算;据此解答。
【精讲精析】(1)14∶21=(14÷7)∶(21÷7)=2∶3
(2)26∶39=(26÷13)∶(39÷13)=2∶3
(3)∶=(×24)∶(×24)=22∶5
(4)1∶=(1×5)∶(×5)=5∶4
(5)0.5∶2.5=(0.5×10)∶(2.5×10)=5∶25=(5÷5)∶(25÷5)=1∶5
(6)0.75∶=∶=(×8)∶(×8)=6∶1
25.556;30;
;80
【解题思路】(1)按照运算顺序,先算乘除法,再算加法;
(2)按照运算顺序,先算除法,再算乘法,最后算减法;
(3)按照运算顺序,有括号先算括号里的除法,再算括号里的加法,最后算括号外面的乘法;
(4)按照运算顺序,先算小括号的减法,再算中括号里的乘法,最后算括号外面的除法。
【精讲精析】(1)15×36+368÷23
(2) 35-1.8÷0.9×2.5
(3)
(4)
26.420÷=980(千克)
【解题思路】看图可知,所求千克数是单位“1”,已知千克数是所求千克数的,已知千克数÷对应分率=所求千克数,据此列式计算。
【精讲精析】420÷=420×=980(千克)
27.240÷(1-20%)
28.14.13cm2; 13.76cm2
【解题思路】通过图可知,由于三角形的内角和是180°,所以第一个图形的三个扇形拼接在一起正好能够构成一个半径是3厘米的半圆,根据半圆的面积公式:S=πr2÷2,把数代入即可求解;
通过图可知,两个半径构成一个正方形边长,即圆的半径:8÷2=4厘米,正方形里面相当于4个的圆,那拼在一起相当于一个半径是4厘米的圆,用正方形的面积-4个圆的面积=涂色部分面积;根据正方形的面积公式:边长×边长,圆的面积公式:S=πr2,把数代入即可求解。
【精讲精析】第一个图形:3.14×32÷2
=3.14×9÷2
=28.26÷2
=14.13(cm2)
第二个图形:8×8-3.14×(8÷2)2
=64-3.14×42
=64-3.14×16
=64-50.24
=13.76(cm2)
29.【解题思路】把圆规的两脚分开,定好两脚的距离,即半径;把有针尖的一只脚固定在一点上,即圆心;把装有铅笔尖的一只脚旋转一周,就画出一个圆。在圆内以一条半径为边,画一个130°的角,两个半径和圆弧围起来的部分就是扇形。
【精讲精析】作图如下:
【要点提示】由圆的两条半径与这两条半径所夹的圆心角所对的弧围成的图形就是扇形。扇形是圆的一部分。
30.【精讲精析】如图:
31.
【解题思路】根据题意,当时未修建完工的里程数是(164-150)千米,已知贵南高铁途经河池市范围总里程数为164千米,求当时未修建完工的里程数占河池市范围总里程数的几分之几,实际上是求一个数占另一个数的几分之几,用除法,用(164-150)除以164,即可得解。
【精讲精析】(164-150)÷164
=14÷164
=
答:当时未修建完工的里程数占河池市范围总里程数的。
【要点提示】此题的解题关键是掌握求一个数占另一个数的几分之几的计算方法。
32.2元
【解题思路】把投币支付每人每次需支付的钱数看作单位“1”,刷卡每人每次需支付的钱数相当于投币支付,根据分数除法的意义,用刷卡每人每次需支付的钱数除以,就是投币支付每人每次需要支付的钱数。
【精讲精析】
(元)
答:投币支付每人每次需2元。
【要点提示】此题是考查分数除法的意义及应用。已知一个数的几分之几是多少,求这个数,用已知数除以它所对应的分率。
33.25岁
【解题思路】求小明今年多少岁.根据“已知量×对应的率”的方法来求问题。可以先求出爸爸的年龄,再求小明的年龄。
【精讲精析】75××
=50×
=25(岁)
答:小明今年25岁。
【要点提示】本题中存在两个单位“1”,第一个是爷爷的年龄、第二个是爸爸的年龄,单位“1”已知用乘法计算,只是要将单位“1”与分率相对应。
34.520元
【解题思路】把一班捐款的金额看作单位“1”,单位“1”已知,根据分数乘法的意义,求一个数的几分之几是多少,用乘法,用一班捐款的金额乘即可求出二班捐款的金额。
【精讲精析】650×=520(元)
答:二班捐款520元。
【要点提示】此题的解题关键是理解分数乘法的意义,掌握求一个数的几分之几是多少的计算方法,从而解决问题。
35.42%
【解题思路】用菜籽油的质量除以油菜籽的质量,求出出油率。
【精讲精析】168÷400×100%=42%
答:这批油菜籽的出油率是42%。
【要点提示】本题考查了百分率的应用,明确出油率的计算方法是解题的关键。
36.157立方厘米
【解题思路】根据题意得出这个铅锤的体积等于下降的水的体积,下降的水的体积是底面半径为10厘米,高为0.5厘米圆柱的体积,根据圆柱的体积=底面积×高即可解答。
【精讲精析】铅锤的体积:
3.14×10×0.5
=3.14×100×0.5
=157(立方厘米)
答:这个铅锤的体积是157立方厘米。
【要点提示】本题考查圆柱的体积,关键是掌握铅锤的体积与下降的水的体积相等。
37.25页
【精讲精析】120×20%÷(1-4%)
=24÷96%
=25(页)
38.八折
【精讲精析】实际利润为:50%×82%=41%;
打折部分利润率为:(41%-50%×70%)÷(1-70%)
=6%÷30%
=20%;
余下部分商品的价格是原价的:(1+20%)÷(1+50%)
=120%÷150%
=80%;
80%即八折.
答:余下部分商品商店是打八折出售的.
【要点提示】本题考查了利润、利润率及折扣问题.要熟练掌握公式:利润=售价-进价;利润率=利润÷进价;折扣=折后的价格÷原价.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
