(期末培优卷)期末核心考点突破提升培优卷-2024-2025学年五年级下学期数学北师大版(含答案解析)
文档属性
| 名称 | (期末培优卷)期末核心考点突破提升培优卷-2024-2025学年五年级下学期数学北师大版(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 538.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末核心考点突破提升培优卷
一、填空题
1.小明的爸爸在超市里买了一桶净含量为6 的玉米油,如果每天吃掉100 ,这桶油可以吃 天。
2.下面是淘淘从家出发,经过公园到学校的路线图。
淘淘从家出发,先向 , °方向步行 米到达公园,然后,从公园出发向 , °方向步行 米到达学校。
3.在横线里填上“>”“<”或“=”.
÷4 4.2× 88÷ 88×
1÷ 1× ÷ × ×
4.骰子的展开图如图所示,骰子相对的两个面的点数和都是7,那么a面上的点数是 ,b面上的点数是 。
5.有两堆苹果,如果从第一堆拿9个放到第二堆,两堆苹果的个数相等;如果从第二堆拿12个放到第一堆,则第一堆苹果的个数是第二堆苹果个数的2倍。原来第一堆有苹果 个,第二堆有苹果 个。
6.某电脑商店四周类出一批电脑,第一周卖出总台数的,第二周类出总台数的,第三周与第四周类出的台数比是5:2,已知第四周比第三周少类出了180台,则这批电脑原有 台。
7.三个连续偶数的和是18,这三个偶数分别是 , , 。
8.一桶水,当水结成冰时体积增加,当冰化成水时体积减少 。
9.一个长方体长、宽、高都扩大2倍,表面积扩大 倍,体积扩大 倍。
10.在73.5%,,0.7255,中,最大的数是 , 最小的数是 。
11.一个长方形的长和宽互为倒数,这个长方形的面积是 。
12.大小两个正方体棱长比是3:2,那么大小两个正方体表面积的比是 ,体积的比是 。
13.在一个边长为3cm的正方体木块的每面中心打一个相通的洞.洞口是边长为1cm的正方形.每个面与正方体相对的面平行(如下图).挖洞后正方体木块的体积是 .
14.两个连续自然数的倒数之和为 ,这两个自然数分别是 和 。
15.在一个底面直径和高都是10厘米的圆柱形玻璃容器内注入8厘米深的水,然后把一块长6厘米,宽5厘米,高8厘米的长方条铁块浸没在水中。则溢出的水的体积是 立方厘米。
二、判断题
16.棱长为6cm的正方体,表面积和体积相等。( )
17.把3个棱长一样的正方体拼成一个长方体,这个长方体的表面积和原来3个正方体表面积的总和相等.( )
18.棱长6分米的正方体,它的表面积和体积相等。
19.分数乘法的意义是求几个相同加数的和的简便运算。( )
20.一个正方体的棱长之和是12cm,则它的体积是1cm3.( )
21.a的 等于b的 (a、b均不为0),那么a比b小。( )
22.正方体、长方体和圆柱体的体积都等于底面积乘高.( )
23.长方体最多有两个面是正方形.( )
三、单选题
24.把 米长的绳子平均分成6段,每段长( )。
A. 米 B. C. 米 D.
25.“转化”是一种重要的数学思想方法。下列选项中用到转化思想的是( )。
①
②2.4×0.8=
③
④把一张纸的平均分成3份,每份是这张纸的几分之几?÷3=×=。
A.①②③ B.①②④ C.②③④ D.①②③④
26.如图,一个长3厘米、宽和高都是2厘米的长方体,从中取下一个棱长1厘米的小正方体,它的表面积( )。
A.变小 B.不变 C.变大 D.不能确定
27.将三个完全一样的正方体拼成一个大长方体之后,表面积( )。
A.不变 B.增加了 C.减少了 D.无法判断
28.把下面的平面展开图折成正方体后,与“脑”相对的面上的字是( )。
A.敢 B.质 C.疑 D.勤
29.下面( )能围成正方体。
A. B. C.
30.明明看一本360页的书.第一天读了全书的,他第二天应从第( )页读起。
A.217 B.216 C.145
31.甲数的小数点向左移动一位,正好和乙数相等,已知甲、乙两数的和是23.1,乙数是( )
A.21 B.2.1 C.0.21 D.11
32.一根长40分米的铁丝焊成一个长方体框架,还余4分米,这个长方体框架中相交于一点的三条棱的长度和是( )分米
A.12 B.9 C.6
33.两个真分数的积一定还是( )。
A.真分数 B.假分数 C.不确定
四、计算题
34.直接写出得数。
× = 2.1× = × = + = + ×0=
× = - × = 2- = ×2.4= ( + )×27=
35.用简便方法计算下面各题。
解方程。
5y-y=4.8
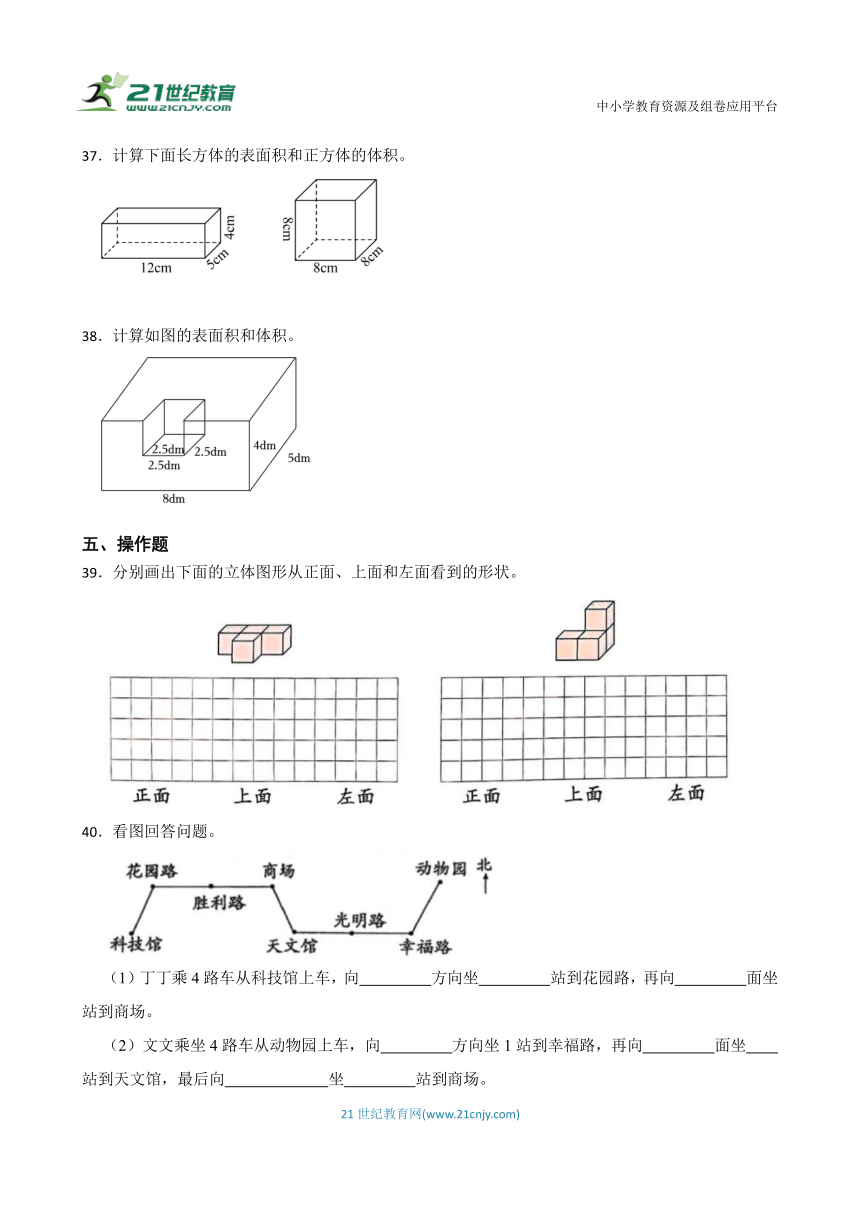
37.计算下面长方体的表面积和正方体的体积。
38.计算如图的表面积和体积。
五、操作题
39.分别画出下面的立体图形从正面、上面和左面看到的形状。
40.看图回答问题。
(1)丁丁乘4路车从科技馆上车,向 方向坐 站到花园路,再向 面坐 站到商场。
(2)文文乘坐4路车从动物园上车,向 方向坐1站到幸福路,再向 面坐 站到天文馆,最后向 坐 站到商场。
六、解决问题
41.实验中学建一个长方体游泳池,长60米,宽25米,深2米.请你算一算.
(1)游泳池的占地面积是多少平方米?
(2)在游泳池底面和内壁抹一层水泥,抹水泥面积是多少平方米?
(3)沿游泳池的内壁1.5米高处用白漆画一条水位线,水位线全长多少米?
42.黄豆中有很多营养成分,蛋白质约占总质量的 ,碳水化合物约占总质量的 。现在有2kg这样的黄豆,含蛋白质和碳水化合物各多少千克
43.6月5日是“世界环境日”。在这一天,六(1)班同学收集塑料瓶和易拉罐共210个,其中塑料瓶的个数是易拉罐的2.5倍。塑料瓶和易拉罐各收集了多少个?(列方程解答)
44.李师傅要做一个棱长是4dm的正方体通风管,至少需要多少平方分米的铁皮?
45.一艘轮船发生漏水事故,船长一边报警一边安排用大功率抽水机向外抽水。当时已经漏进450桶水,抽水机每分抽30桶,经过25分把水抽完,每分漏进多少桶水?(用方程解)
46.一杯250mL的鲜牛奶含有 g的钙质,占一个成年人一天所需钙质的 .一个成年人一天需要多少钙质?
47.A、B两地间的公路长为400km.甲、乙两辆汽车从两地相向而行,甲车每小时行42km,乙车每小时行38km.两车同时出发,经过多少小时两车相遇?(列方程解决问题)
48.有一个正方体容器,棱长是 40 cm,里面水面高35 cm。有一根长50 cm横截面是400 cm2的长方体铁棒现将铁棒垂直插入水中,会溢出多少升的水?
49.一种长方体影集长20厘米,宽15厘米,厚4厘米。现在要用硬纸板给它做一个封套(右侧不用封),至少要多大面积的硬纸板?
50.一个近似的圆锥形谷堆,底面半径是4m,高是3m。把这堆谷子铺在一个长5m,宽2m的长方体粮仓里,这些谷子铺平能有多高?
参考答案及试题解析
1.升;毫升;60
【解析】解:小明的爸爸在超市里买了一桶净含量为6升的玉米油,如果每天吃掉100毫升,6升=6000毫升,6000÷100=60天,所以这桶油可以吃60天。
故答案为:升;毫升;60。
【分析】先填上合适的单位,然后把单位进行换算,即1升=1000毫升,那么这桶油可以吃的天数=这桶油的毫升数÷每天吃掉的毫升数。
2.北偏东;60;1000;南偏东;60;800
【解析】 淘淘从家出发,先向北偏东,60°方向步行1000米到达公园,然后,从公园出发向南偏东,60°方向步行800米到达学校。
故答案为:北偏东;60;1000;南偏东;60;800。
【分析】此题主要考查了路线图的知识,此图是按“上北下南,左西右东”来规定方向的,图上距离1厘米表示实际距离200米,根据方向和距离描述淘淘上学的路线图。
3.<;>;>;>;>;>
【解析】解:4>1,所以÷4<;4.2>1,所以4.2×>;<1,所以88÷>88×;
<1,所以1÷>1×;<1,所以÷>;>,所以×>×。
故答案为:<;>;>;>;>;>。
【分析】一个非0数乘一个大于1的数,积大于这个数,乘一个小于1的数,积小于这个数;一个非0数除以一个大于1的数,商小于这个数,除以一个小于1的数,商大于这个数。
4.4;6
【解析】 解:折成正方体后,a面的对面点数是3,b面的对面点数是1。
7-3=4
7-1=6
a面上的点数是4,b面上的点数是6。
故答案为:4;6。
【分析】此图属于正方体展开图的“2-2-2”型,折成正方体后,a面的对面点数是3,b面的对面点数是1,c面的对面点数是2,已知相对的两个面的点数和都是7,据此即可求出a面上的点数、b面上的点数。据此解答。
5.72;54
【解析】解:设原来第二堆有x个苹果,则第一堆原来有(x+18)个苹果。
x+18+12=(x-12)×2
x+30=2x-24
2x-24=x+30
2x-24-x=30
x-24=30
x=30+24
x=54
54+18=72(个)
则原来第一堆有72个苹果,第二堆有54个苹果。
故答案为:72;54.
【分析】如果从第一堆拿9个放到第二堆,两堆苹果的个数相等,可知第一堆比第二堆多18个苹果,据此设未知数;
本题等量关系:原来第一堆苹果的个数+12个=(原来第二堆苹果个数-12个)×2倍,根据等量关系列方程,根据等式性质解方程。
6.640
【解析】解:180÷(5-2)×(5+2)
=180÷3×7
=60×7
=420(台)
420÷()
=420÷
=640(台)
故答案为:640。
【分析】已知第三周与第四周卖出的台数比是5:2,可将第三周卖出的台数看作5份,第四周卖出的台数看作2份,则第三周与第四周相差3份,用180除以3求出每份是多少,再乘(5+2)求出第三周和第四周一共卖出的台数。把这批电脑看作单位“1”,减去第一周和第二周卖出的分率,正好与第三周和第四周共卖出的台数相对应,用除法求出这批电脑的总台数。
7.4;6;8
8.
【解析】解:当水结成冰时,水是单位“1”,冰是
当冰化成水时,,冰是单位“1”
故答案为:。
【分析】根据当水结成冰时,体积增加了,假没这一桶水的体积是单位“1”,则结成冰时,冰的体积应是:1+1×=;当冰化成水时,体积减少了几分之几,此时单位“1”是冰,所以列式为(10-9)÷10,计算此式即可得出结果。
9.4;8
【解析】 一个长方体长、宽、高都扩大2倍,表面积扩大2×2=4倍,体积扩大2×2×2=8倍。
故答案为:4;8。
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,一个长方体长、宽、高都扩大a倍,表面积扩大a2倍,体积扩大a3倍,据此列式解答。
10.;
【解析】解:73.5%=0.735, =0.777……, =0.72525……
所以>73.5%> 0.7255 >
故答案为:;
【分析】先把百分数和分数化成小数,先比较整数部分,若整数部分一样,再比较小数部分即可比较出结果。为:>73.5%> 0.7255 >
11.1
【解析】解:长×宽=1,这个长方形的面积是1。
故答案为:1。
【分析】乘积是1的两个数互为倒数。
12.9:4;27:8
【解析】解:大小两个正方体表面积的比是32:22=9:4,体积的比是33:23=27:8。
故答案为:9:4;27:8。
【分析】正方体的表面积的比等于棱长的平方之比;正方体的体积之比等于棱长的立平方之比。
13.20
【解析】3×3×3-1×1×3×3+1×1×1×2
=9×3-9+2
=27-9+2
=18+2
=20(cm3)
故答案为:20.
【分析】根据题意可知,先求出这个大正方体的体积,用公式:正方体的体积=棱长×棱长×棱长;
然后求出挖的3个洞的体积,3个洞的形状都是长方体,洞口部分是边长为1cm的正方形,洞深3cm,中间公共部分是棱长1cm的小正方体,所以用正方体的体积-3个洞的体积+多减的中心部分2个正方体体积=挖洞后的正方体木块的体积,据此列式解答.
14.3;4
【解析】解:因为 ,所以这两个连续自然数是3和4。
故答案为:3;4
【分析】由题意可知,这两个自然数的积是12,和是7,只有3与4的积是12,和是7,因此这两个自然数分别是3和4。
15.83
【解析】解:圆柱的底面半径:10÷2=5(厘米)
圆柱的底面积:3.14×5×5=78.5(立方厘米)
78.5×8+6×5×8-78.5×10
=628+240-785
=83(立方厘米)
故答案为:83。
【分析】圆柱内水的体积+长方条铁块的体积-圆柱能容纳的水的体积=溢出的水的体积。
16.错误
【解析】表面积和体积不能比较大小,原题说法错误。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,表面积和体积是不同的两种量,无法比较大小,据此判断。
17.错误
【解析】把3个棱长一样的正方体拼成一个长方体,这个长方体的表面积比原来3个正方体表面积的总和要少,原题说法错误.
故答案为:错误.
【分析】根据题意可知,把3个棱长一样的正方体拼成一个长方体,会减少4个正方形面的面积,所以这个长方体的表面积比原来3个正方体表面积的总和要少,据此解答.
18.错误
【解析】解:表面积为:6×6×6=216(平方分米),体积为:6×6×6=216(立方分米),数值相等,单位不同,不能比较大小,故原题说法错误.
故答案为:错误.
【分析】表面积和体积不是同一个量,不能比较大小,据此判断即可.
19.错误
【解析】解:分数乘整数的意义,与整数乘法的意义相同,就是求几个相同加数的和的简便运算;一个数乘分数的意义是求一个数的几分之几是多少,所以原题干说法错误。
故答案为:错误。
【分析】分数乘整数的意义,就是求几个相同加数的和的简便运算;一个数乘分数的意义是求一个数的几分之几是多少。
20.正确
【解析】解:棱长:12÷12=1(cm),体积:1×1×1=1(cm3),所以一个正方体的棱长之和是12cm,则它的体积是1cm3。原题说法正确。
故答案为:正确。
【分析】正方体棱长和=棱长×12,正方体体积=棱长×棱长×棱长,先计算棱长,再计算体积即可。
21.正确
【解析】设a=4,4× =1,b=1÷ =5,5>4,即b>a,由此可知题干所述正确。
故答案为:正确。
【分析】在a× =b× 中,>,所以a<b。
22.正确
【解析】解:因为正方体、长方体和圆柱体的体积都可以用底面积乘高来求,即V=sh;
所以原题说法是正确的;
故答案为:正确.
【分析】因为正方体、长方体和圆柱体的体积都可以用底面积乘高来求,即V=sh,所以原题说法是正确的.
23.正确
【解析】解:长方体最多有两个面是正方形。
故答案为:正确。
【分析】根据长方体的特征,一般情况6个面都是长方形,特殊情况有两个相对的面是正方形,据此判断即可。
24.C
【解析】解:÷6=(米)
故答案为:C。
【分析】用绳子的总长度除以平均分的段数即可求出每段的实际长度。
25.D
26.C
【解析】解:看图可知,挖去这个小正方体后,表面积减少了2个小正方形的面,同时增加了4个小正方形的面,所以它的表面积变大。
故答案为:C。
【分析】表面积是物体表面所有面的面积之和,判断出挖去一个正方体后增加和减少小正方形面的个数,然后判断表面积的变化情况。
27.C
【解析】
将三个完全一样的正方体拼成一个大长方体之后,肯定有重合的面,所以表面积会减少。
故答案为:C。
【分析】组合图形的面有被遮挡重合的,所以它的表面积和三个正方体相比,肯定会减少。
28.C
29.B
【解析】解:选项A,不能围成正方体;
选项B,能围成正方体;
选项C,不能围成正方体。
故答案为:B。
【分析】正方体展开有11种,规律如下:中间4个一连串,两边各一随便放;二三紧连错一个,三一相连一随意;两两相连各错一。三个两排一对齐。先找同层隔一面,再找异层隔两面,剩下两面必相对,两个起头按顺序。
30.A
【解析】解:360× +1
=216+1
=217(页)。
故答案为:A。
【分析】他第二天应开始看的页数=这本书的总页数×第一天看的分率+1页。
31.B
【解析】解:设乙数是x,则甲数是10x。
x+10x=23.1
11x=23.1
x=2.1
故答案为:B
【分析】甲数的小数点向左移动一位,正好和乙数相等,说明甲数是乙数的10倍,设乙数是x,则甲数是10x;等量关系:甲数10x+乙数x=23.1,根据等量关系列方程,根据等式性质2解方程。
32.B
【解析】长方体由12条棱组成,而12条棱分为长、宽、高各4条,长方体棱长总和÷4就是一组长宽高的和
解法:(40-4)÷4,
=36÷4,
=9(分米);
答:相交于一点的三条棱的长度和是9分米.
故选:B
33.A
【解析】解:因为真分数小于1,一个非0的数乘小于1的数,积小于原来的数,所以两个真分数的积一定还是真分数。
故答案为:A。
【分析】一个非0的数乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
34. × = 2.1× =1.5 × = + = + ×0=
× = - × = 2- = ×2.4=0.9 ( + )×27=
【解析】分数与分数相乘,用分子相乘的积做分子,分母相乘的积做分母,能约分的要约分;
分数乘小数,可以先把小数化成分数,然后计算即可;
异分母分数加减法,先通分把分数化成同分母分数,然后把分子相加减即可。
35.解:
=
=+1
=
=
=-1
=
=
=
=
=
=1-
=
【解析】(1)运用加法结合律进行简算;
(2)(3)运用减法的性质简算;
(4)运用加法交换律和加法结合律简算。
36.
解:x=-
x=
解:x=+
x=
5y-y=4.8
解:4y=4.8
y=4.8÷4
y=1.2
解: x-=1-
x-=
x= +
x=
解: -x= -
-x=
x=-
x=
解: -x=-
-x=
x=-
x=
【解析】根据加减法之间的关系,乘除法之间的关系解答;
第一题:和-一个加数=另一个加数;
第二题:被减数=差+减数;
第三题:积÷一个因数=另一个因数;
第四题:减数=被减数-差,被减数=差+减数;
第五题:和-一个加数=另一个加数,减数=被减数-差;
第六题:和-一个加数=另一个加数,减数=被减数-差。
37.256cm2;512cm3
38.解:(8×5+8×4+5×4)×2+2.5×2.5×2
=(40+32+20)×2+6.25×2
=92×2+12.5
=184+12.5
=196.5(平方分米)
8×5×4﹣2.5×2.5×2.5
=40×4﹣6.25×2.5
=160﹣15.625
=144.375(立方分米)
答:它的表面积是196.2平方分米,体积是144.375立方分米。
【解析】挖去一个正方体后,表面积减少了2个小正方形面的面积,同时增加了4个小正方形面的面积,所以表面积实际比原来长方体的表面积增加了两个边长2.5分米的正方形面的面积。用原来长方体的体积减去挖去部分正方体的体积即可求出图形的体积。
39.解:左边的图:
右边的图:
【解析】左边的图:
从前面看到一横列,共3个小正方形;
从左面看到一横列,共2个小正方形;
从上面看到三竖列,第一竖列有1个小正方形,第二竖列有2个小正方形,第三竖列有1个小正方形,这三竖列上面对齐。
右边的图:
从前面看到两竖列,第一竖列有1个小正方形,第二竖列有2个小正方形;
从左面看到两竖列,第一竖列有2个小正方形,第二竖列有1个小正方形;
从上面看到两竖列,第一竖列有1个小正方形,第二竖列有2个小正方形,这两竖列下面对齐。
40.(1)东北;1;东;2
(2)西南;西;2;西北方向;1
【解析】解:(1)丁丁乘4路车从科技馆上车,向东北方向坐1站到花园路,再向东面坐2站到商场。
(2)文文乘坐4路车从动物园上车,向西南方向坐1站到幸福路,再向西面坐2站到天文馆,最后向西北方向坐1站到商场。
故答案为:(1)东北;1;东;2;(2)西南;西;2;西北方向;1。
【分析】描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和距离。
41.(1)解:60×25=1500(平方米)
答:游泳池的占地面积是1500平方米。
(2)解:60×25+60×2×2+25×2×2
=1500+240+100
=1840(平方米)
答:抹水泥面积是1840平方米。
(3)解:60×2+25×2
=120+50
=170(米)
答:水位线全长170米。
【解析】(1)要求游泳池的占地面积,用长×宽=长方体的占地面积,据此列式解答;
(2)要求在游泳池底面和内壁抹一层水泥,抹水泥面积是多少平方米,就是求无盖长方体的表面积,用公式:无盖长方体的表面积=长×宽+长×高×2+宽×高×2,据此列式解答;
(3) 沿游泳池的内壁1.5米高处用白漆画一条水位线,要求水位线的长度,就是求两条长与两条宽的长度之和,据此列式解答.
42.解:2×=(千克)
2×=(千克)
答:含蛋白质千克,碳水化合物千克。
【解析】根据题意可知,黄豆的总质量×蛋白质约占总质量的分率=蛋白质的质量, 黄豆的总质量×碳水化合物约占总质量的分率=碳水化合物的质量,据此列式解答。
43.解:设收集易拉罐x个,则收集塑料瓶2.5x个。
x+2.5x=210
3.5x=210
x=210÷3.5
x=60
2.5×60=150(个)
答:收集易拉罐60个,则收集塑料瓶150个。
【解析】等量关系:收集易拉罐个数+收集塑料瓶个数=210个,根据等量关系列方程,根据等式性质解方程。
44.解:64×4×4
=16×4
=64(平方分米)
答:至少需要64平方分米的铁皮。
【解析】正方体的表面积=棱长×棱长×6,本题中由于是通风管,则缺少两个面,所以铁皮的面积=棱长×棱长×4,代入数值计算即可。
45.解:设每分钟漏进x桶水。
25x+450=30×25
25x+450=750
25x=300
x=12
答:每分漏进12桶水。
【解析】本题可以设每分钟漏进x桶水,题中存在的等量关系是:每分钟漏进水的桶数×抽完用的时间+已经漏进的桶数=抽水机每分抽水的桶数×抽完用的时间,据此代入字母和数据作答即可。
46.解: ÷ = (g)
答:一个成年人一天需要 g钙。
【解析】一个成年人一天需要钙质的克数=一杯鲜牛奶含有钙质的克数÷一杯鲜牛奶含有钙质的克数占一个成年人一天所需钙质的几分之几,据此代入数据作答即可。
47.解:设经过x小时两车相遇。
(42+38)×x=400
80x=400
80x÷80=400÷80
x=5
答:经过5小时两车相遇。
【解析】此题主要考查了列方程解决相遇应用题,设经过x小时两车相遇,(甲车的速度+乙车的速度)×相遇时间=总路程,据此列方程解答。
48.解:400×40=16000(cm3)
40×40×(40-35)
=1600×5
=8000(cm3)
16000-8000=8000(cm3)=8(dm3)=8(L)
答:会溢出8升的水。
【解析】长方体铁棒放在容器中的体积=铁棒的横截面积×铁棒的长度,水面以上空间的体积=正方体容器的棱长×正方体容器的棱长×原来水面以上的高度,所以溢出水的体积=长方体铁棒放在容器中的体积-水面以上空间的体积。
49.解:(20×15+20×4)×2+15×4
=(300+80)×2+15×4
=380×2+15×4
=760+60
=820(平方厘米)
答:至少要820平方厘米的硬纸板。
【解析】至少要硬纸板的面积=(长×宽+长×高)×2+宽×高。
50.解:×3.14×42×3÷(5×2)
=×3.14×16×3÷10
=50.24÷10
=5.024(米)
答:这些稻谷铺平能有5.024米。
【解析】这些稻谷铺平后的高度=×π×半径2×圆锥的高÷(长方体粮仓的长×宽)。
21世纪教育网(www.21cnjy.com)
2024-2025学年五年级下册数学期末核心考点突破提升培优卷
一、填空题
1.小明的爸爸在超市里买了一桶净含量为6 的玉米油,如果每天吃掉100 ,这桶油可以吃 天。
2.下面是淘淘从家出发,经过公园到学校的路线图。
淘淘从家出发,先向 , °方向步行 米到达公园,然后,从公园出发向 , °方向步行 米到达学校。
3.在横线里填上“>”“<”或“=”.
÷4 4.2× 88÷ 88×
1÷ 1× ÷ × ×
4.骰子的展开图如图所示,骰子相对的两个面的点数和都是7,那么a面上的点数是 ,b面上的点数是 。
5.有两堆苹果,如果从第一堆拿9个放到第二堆,两堆苹果的个数相等;如果从第二堆拿12个放到第一堆,则第一堆苹果的个数是第二堆苹果个数的2倍。原来第一堆有苹果 个,第二堆有苹果 个。
6.某电脑商店四周类出一批电脑,第一周卖出总台数的,第二周类出总台数的,第三周与第四周类出的台数比是5:2,已知第四周比第三周少类出了180台,则这批电脑原有 台。
7.三个连续偶数的和是18,这三个偶数分别是 , , 。
8.一桶水,当水结成冰时体积增加,当冰化成水时体积减少 。
9.一个长方体长、宽、高都扩大2倍,表面积扩大 倍,体积扩大 倍。
10.在73.5%,,0.7255,中,最大的数是 , 最小的数是 。
11.一个长方形的长和宽互为倒数,这个长方形的面积是 。
12.大小两个正方体棱长比是3:2,那么大小两个正方体表面积的比是 ,体积的比是 。
13.在一个边长为3cm的正方体木块的每面中心打一个相通的洞.洞口是边长为1cm的正方形.每个面与正方体相对的面平行(如下图).挖洞后正方体木块的体积是 .
14.两个连续自然数的倒数之和为 ,这两个自然数分别是 和 。
15.在一个底面直径和高都是10厘米的圆柱形玻璃容器内注入8厘米深的水,然后把一块长6厘米,宽5厘米,高8厘米的长方条铁块浸没在水中。则溢出的水的体积是 立方厘米。
二、判断题
16.棱长为6cm的正方体,表面积和体积相等。( )
17.把3个棱长一样的正方体拼成一个长方体,这个长方体的表面积和原来3个正方体表面积的总和相等.( )
18.棱长6分米的正方体,它的表面积和体积相等。
19.分数乘法的意义是求几个相同加数的和的简便运算。( )
20.一个正方体的棱长之和是12cm,则它的体积是1cm3.( )
21.a的 等于b的 (a、b均不为0),那么a比b小。( )
22.正方体、长方体和圆柱体的体积都等于底面积乘高.( )
23.长方体最多有两个面是正方形.( )
三、单选题
24.把 米长的绳子平均分成6段,每段长( )。
A. 米 B. C. 米 D.
25.“转化”是一种重要的数学思想方法。下列选项中用到转化思想的是( )。
①
②2.4×0.8=
③
④把一张纸的平均分成3份,每份是这张纸的几分之几?÷3=×=。
A.①②③ B.①②④ C.②③④ D.①②③④
26.如图,一个长3厘米、宽和高都是2厘米的长方体,从中取下一个棱长1厘米的小正方体,它的表面积( )。
A.变小 B.不变 C.变大 D.不能确定
27.将三个完全一样的正方体拼成一个大长方体之后,表面积( )。
A.不变 B.增加了 C.减少了 D.无法判断
28.把下面的平面展开图折成正方体后,与“脑”相对的面上的字是( )。
A.敢 B.质 C.疑 D.勤
29.下面( )能围成正方体。
A. B. C.
30.明明看一本360页的书.第一天读了全书的,他第二天应从第( )页读起。
A.217 B.216 C.145
31.甲数的小数点向左移动一位,正好和乙数相等,已知甲、乙两数的和是23.1,乙数是( )
A.21 B.2.1 C.0.21 D.11
32.一根长40分米的铁丝焊成一个长方体框架,还余4分米,这个长方体框架中相交于一点的三条棱的长度和是( )分米
A.12 B.9 C.6
33.两个真分数的积一定还是( )。
A.真分数 B.假分数 C.不确定
四、计算题
34.直接写出得数。
× = 2.1× = × = + = + ×0=
× = - × = 2- = ×2.4= ( + )×27=
35.用简便方法计算下面各题。
解方程。
5y-y=4.8
37.计算下面长方体的表面积和正方体的体积。
38.计算如图的表面积和体积。
五、操作题
39.分别画出下面的立体图形从正面、上面和左面看到的形状。
40.看图回答问题。
(1)丁丁乘4路车从科技馆上车,向 方向坐 站到花园路,再向 面坐 站到商场。
(2)文文乘坐4路车从动物园上车,向 方向坐1站到幸福路,再向 面坐 站到天文馆,最后向 坐 站到商场。
六、解决问题
41.实验中学建一个长方体游泳池,长60米,宽25米,深2米.请你算一算.
(1)游泳池的占地面积是多少平方米?
(2)在游泳池底面和内壁抹一层水泥,抹水泥面积是多少平方米?
(3)沿游泳池的内壁1.5米高处用白漆画一条水位线,水位线全长多少米?
42.黄豆中有很多营养成分,蛋白质约占总质量的 ,碳水化合物约占总质量的 。现在有2kg这样的黄豆,含蛋白质和碳水化合物各多少千克
43.6月5日是“世界环境日”。在这一天,六(1)班同学收集塑料瓶和易拉罐共210个,其中塑料瓶的个数是易拉罐的2.5倍。塑料瓶和易拉罐各收集了多少个?(列方程解答)
44.李师傅要做一个棱长是4dm的正方体通风管,至少需要多少平方分米的铁皮?
45.一艘轮船发生漏水事故,船长一边报警一边安排用大功率抽水机向外抽水。当时已经漏进450桶水,抽水机每分抽30桶,经过25分把水抽完,每分漏进多少桶水?(用方程解)
46.一杯250mL的鲜牛奶含有 g的钙质,占一个成年人一天所需钙质的 .一个成年人一天需要多少钙质?
47.A、B两地间的公路长为400km.甲、乙两辆汽车从两地相向而行,甲车每小时行42km,乙车每小时行38km.两车同时出发,经过多少小时两车相遇?(列方程解决问题)
48.有一个正方体容器,棱长是 40 cm,里面水面高35 cm。有一根长50 cm横截面是400 cm2的长方体铁棒现将铁棒垂直插入水中,会溢出多少升的水?
49.一种长方体影集长20厘米,宽15厘米,厚4厘米。现在要用硬纸板给它做一个封套(右侧不用封),至少要多大面积的硬纸板?
50.一个近似的圆锥形谷堆,底面半径是4m,高是3m。把这堆谷子铺在一个长5m,宽2m的长方体粮仓里,这些谷子铺平能有多高?
参考答案及试题解析
1.升;毫升;60
【解析】解:小明的爸爸在超市里买了一桶净含量为6升的玉米油,如果每天吃掉100毫升,6升=6000毫升,6000÷100=60天,所以这桶油可以吃60天。
故答案为:升;毫升;60。
【分析】先填上合适的单位,然后把单位进行换算,即1升=1000毫升,那么这桶油可以吃的天数=这桶油的毫升数÷每天吃掉的毫升数。
2.北偏东;60;1000;南偏东;60;800
【解析】 淘淘从家出发,先向北偏东,60°方向步行1000米到达公园,然后,从公园出发向南偏东,60°方向步行800米到达学校。
故答案为:北偏东;60;1000;南偏东;60;800。
【分析】此题主要考查了路线图的知识,此图是按“上北下南,左西右东”来规定方向的,图上距离1厘米表示实际距离200米,根据方向和距离描述淘淘上学的路线图。
3.<;>;>;>;>;>
【解析】解:4>1,所以÷4<;4.2>1,所以4.2×>;<1,所以88÷>88×;
<1,所以1÷>1×;<1,所以÷>;>,所以×>×。
故答案为:<;>;>;>;>;>。
【分析】一个非0数乘一个大于1的数,积大于这个数,乘一个小于1的数,积小于这个数;一个非0数除以一个大于1的数,商小于这个数,除以一个小于1的数,商大于这个数。
4.4;6
【解析】 解:折成正方体后,a面的对面点数是3,b面的对面点数是1。
7-3=4
7-1=6
a面上的点数是4,b面上的点数是6。
故答案为:4;6。
【分析】此图属于正方体展开图的“2-2-2”型,折成正方体后,a面的对面点数是3,b面的对面点数是1,c面的对面点数是2,已知相对的两个面的点数和都是7,据此即可求出a面上的点数、b面上的点数。据此解答。
5.72;54
【解析】解:设原来第二堆有x个苹果,则第一堆原来有(x+18)个苹果。
x+18+12=(x-12)×2
x+30=2x-24
2x-24=x+30
2x-24-x=30
x-24=30
x=30+24
x=54
54+18=72(个)
则原来第一堆有72个苹果,第二堆有54个苹果。
故答案为:72;54.
【分析】如果从第一堆拿9个放到第二堆,两堆苹果的个数相等,可知第一堆比第二堆多18个苹果,据此设未知数;
本题等量关系:原来第一堆苹果的个数+12个=(原来第二堆苹果个数-12个)×2倍,根据等量关系列方程,根据等式性质解方程。
6.640
【解析】解:180÷(5-2)×(5+2)
=180÷3×7
=60×7
=420(台)
420÷()
=420÷
=640(台)
故答案为:640。
【分析】已知第三周与第四周卖出的台数比是5:2,可将第三周卖出的台数看作5份,第四周卖出的台数看作2份,则第三周与第四周相差3份,用180除以3求出每份是多少,再乘(5+2)求出第三周和第四周一共卖出的台数。把这批电脑看作单位“1”,减去第一周和第二周卖出的分率,正好与第三周和第四周共卖出的台数相对应,用除法求出这批电脑的总台数。
7.4;6;8
8.
【解析】解:当水结成冰时,水是单位“1”,冰是
当冰化成水时,,冰是单位“1”
故答案为:。
【分析】根据当水结成冰时,体积增加了,假没这一桶水的体积是单位“1”,则结成冰时,冰的体积应是:1+1×=;当冰化成水时,体积减少了几分之几,此时单位“1”是冰,所以列式为(10-9)÷10,计算此式即可得出结果。
9.4;8
【解析】 一个长方体长、宽、高都扩大2倍,表面积扩大2×2=4倍,体积扩大2×2×2=8倍。
故答案为:4;8。
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,一个长方体长、宽、高都扩大a倍,表面积扩大a2倍,体积扩大a3倍,据此列式解答。
10.;
【解析】解:73.5%=0.735, =0.777……, =0.72525……
所以>73.5%> 0.7255 >
故答案为:;
【分析】先把百分数和分数化成小数,先比较整数部分,若整数部分一样,再比较小数部分即可比较出结果。为:>73.5%> 0.7255 >
11.1
【解析】解:长×宽=1,这个长方形的面积是1。
故答案为:1。
【分析】乘积是1的两个数互为倒数。
12.9:4;27:8
【解析】解:大小两个正方体表面积的比是32:22=9:4,体积的比是33:23=27:8。
故答案为:9:4;27:8。
【分析】正方体的表面积的比等于棱长的平方之比;正方体的体积之比等于棱长的立平方之比。
13.20
【解析】3×3×3-1×1×3×3+1×1×1×2
=9×3-9+2
=27-9+2
=18+2
=20(cm3)
故答案为:20.
【分析】根据题意可知,先求出这个大正方体的体积,用公式:正方体的体积=棱长×棱长×棱长;
然后求出挖的3个洞的体积,3个洞的形状都是长方体,洞口部分是边长为1cm的正方形,洞深3cm,中间公共部分是棱长1cm的小正方体,所以用正方体的体积-3个洞的体积+多减的中心部分2个正方体体积=挖洞后的正方体木块的体积,据此列式解答.
14.3;4
【解析】解:因为 ,所以这两个连续自然数是3和4。
故答案为:3;4
【分析】由题意可知,这两个自然数的积是12,和是7,只有3与4的积是12,和是7,因此这两个自然数分别是3和4。
15.83
【解析】解:圆柱的底面半径:10÷2=5(厘米)
圆柱的底面积:3.14×5×5=78.5(立方厘米)
78.5×8+6×5×8-78.5×10
=628+240-785
=83(立方厘米)
故答案为:83。
【分析】圆柱内水的体积+长方条铁块的体积-圆柱能容纳的水的体积=溢出的水的体积。
16.错误
【解析】表面积和体积不能比较大小,原题说法错误。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长,表面积和体积是不同的两种量,无法比较大小,据此判断。
17.错误
【解析】把3个棱长一样的正方体拼成一个长方体,这个长方体的表面积比原来3个正方体表面积的总和要少,原题说法错误.
故答案为:错误.
【分析】根据题意可知,把3个棱长一样的正方体拼成一个长方体,会减少4个正方形面的面积,所以这个长方体的表面积比原来3个正方体表面积的总和要少,据此解答.
18.错误
【解析】解:表面积为:6×6×6=216(平方分米),体积为:6×6×6=216(立方分米),数值相等,单位不同,不能比较大小,故原题说法错误.
故答案为:错误.
【分析】表面积和体积不是同一个量,不能比较大小,据此判断即可.
19.错误
【解析】解:分数乘整数的意义,与整数乘法的意义相同,就是求几个相同加数的和的简便运算;一个数乘分数的意义是求一个数的几分之几是多少,所以原题干说法错误。
故答案为:错误。
【分析】分数乘整数的意义,就是求几个相同加数的和的简便运算;一个数乘分数的意义是求一个数的几分之几是多少。
20.正确
【解析】解:棱长:12÷12=1(cm),体积:1×1×1=1(cm3),所以一个正方体的棱长之和是12cm,则它的体积是1cm3。原题说法正确。
故答案为:正确。
【分析】正方体棱长和=棱长×12,正方体体积=棱长×棱长×棱长,先计算棱长,再计算体积即可。
21.正确
【解析】设a=4,4× =1,b=1÷ =5,5>4,即b>a,由此可知题干所述正确。
故答案为:正确。
【分析】在a× =b× 中,>,所以a<b。
22.正确
【解析】解:因为正方体、长方体和圆柱体的体积都可以用底面积乘高来求,即V=sh;
所以原题说法是正确的;
故答案为:正确.
【分析】因为正方体、长方体和圆柱体的体积都可以用底面积乘高来求,即V=sh,所以原题说法是正确的.
23.正确
【解析】解:长方体最多有两个面是正方形。
故答案为:正确。
【分析】根据长方体的特征,一般情况6个面都是长方形,特殊情况有两个相对的面是正方形,据此判断即可。
24.C
【解析】解:÷6=(米)
故答案为:C。
【分析】用绳子的总长度除以平均分的段数即可求出每段的实际长度。
25.D
26.C
【解析】解:看图可知,挖去这个小正方体后,表面积减少了2个小正方形的面,同时增加了4个小正方形的面,所以它的表面积变大。
故答案为:C。
【分析】表面积是物体表面所有面的面积之和,判断出挖去一个正方体后增加和减少小正方形面的个数,然后判断表面积的变化情况。
27.C
【解析】
将三个完全一样的正方体拼成一个大长方体之后,肯定有重合的面,所以表面积会减少。
故答案为:C。
【分析】组合图形的面有被遮挡重合的,所以它的表面积和三个正方体相比,肯定会减少。
28.C
29.B
【解析】解:选项A,不能围成正方体;
选项B,能围成正方体;
选项C,不能围成正方体。
故答案为:B。
【分析】正方体展开有11种,规律如下:中间4个一连串,两边各一随便放;二三紧连错一个,三一相连一随意;两两相连各错一。三个两排一对齐。先找同层隔一面,再找异层隔两面,剩下两面必相对,两个起头按顺序。
30.A
【解析】解:360× +1
=216+1
=217(页)。
故答案为:A。
【分析】他第二天应开始看的页数=这本书的总页数×第一天看的分率+1页。
31.B
【解析】解:设乙数是x,则甲数是10x。
x+10x=23.1
11x=23.1
x=2.1
故答案为:B
【分析】甲数的小数点向左移动一位,正好和乙数相等,说明甲数是乙数的10倍,设乙数是x,则甲数是10x;等量关系:甲数10x+乙数x=23.1,根据等量关系列方程,根据等式性质2解方程。
32.B
【解析】长方体由12条棱组成,而12条棱分为长、宽、高各4条,长方体棱长总和÷4就是一组长宽高的和
解法:(40-4)÷4,
=36÷4,
=9(分米);
答:相交于一点的三条棱的长度和是9分米.
故选:B
33.A
【解析】解:因为真分数小于1,一个非0的数乘小于1的数,积小于原来的数,所以两个真分数的积一定还是真分数。
故答案为:A。
【分析】一个非0的数乘小于1的数,所得的积小于原来的数,反之,积大于原来的数。
34. × = 2.1× =1.5 × = + = + ×0=
× = - × = 2- = ×2.4=0.9 ( + )×27=
【解析】分数与分数相乘,用分子相乘的积做分子,分母相乘的积做分母,能约分的要约分;
分数乘小数,可以先把小数化成分数,然后计算即可;
异分母分数加减法,先通分把分数化成同分母分数,然后把分子相加减即可。
35.解:
=
=+1
=
=
=-1
=
=
=
=
=
=1-
=
【解析】(1)运用加法结合律进行简算;
(2)(3)运用减法的性质简算;
(4)运用加法交换律和加法结合律简算。
36.
解:x=-
x=
解:x=+
x=
5y-y=4.8
解:4y=4.8
y=4.8÷4
y=1.2
解: x-=1-
x-=
x= +
x=
解: -x= -
-x=
x=-
x=
解: -x=-
-x=
x=-
x=
【解析】根据加减法之间的关系,乘除法之间的关系解答;
第一题:和-一个加数=另一个加数;
第二题:被减数=差+减数;
第三题:积÷一个因数=另一个因数;
第四题:减数=被减数-差,被减数=差+减数;
第五题:和-一个加数=另一个加数,减数=被减数-差;
第六题:和-一个加数=另一个加数,减数=被减数-差。
37.256cm2;512cm3
38.解:(8×5+8×4+5×4)×2+2.5×2.5×2
=(40+32+20)×2+6.25×2
=92×2+12.5
=184+12.5
=196.5(平方分米)
8×5×4﹣2.5×2.5×2.5
=40×4﹣6.25×2.5
=160﹣15.625
=144.375(立方分米)
答:它的表面积是196.2平方分米,体积是144.375立方分米。
【解析】挖去一个正方体后,表面积减少了2个小正方形面的面积,同时增加了4个小正方形面的面积,所以表面积实际比原来长方体的表面积增加了两个边长2.5分米的正方形面的面积。用原来长方体的体积减去挖去部分正方体的体积即可求出图形的体积。
39.解:左边的图:
右边的图:
【解析】左边的图:
从前面看到一横列,共3个小正方形;
从左面看到一横列,共2个小正方形;
从上面看到三竖列,第一竖列有1个小正方形,第二竖列有2个小正方形,第三竖列有1个小正方形,这三竖列上面对齐。
右边的图:
从前面看到两竖列,第一竖列有1个小正方形,第二竖列有2个小正方形;
从左面看到两竖列,第一竖列有2个小正方形,第二竖列有1个小正方形;
从上面看到两竖列,第一竖列有1个小正方形,第二竖列有2个小正方形,这两竖列下面对齐。
40.(1)东北;1;东;2
(2)西南;西;2;西北方向;1
【解析】解:(1)丁丁乘4路车从科技馆上车,向东北方向坐1站到花园路,再向东面坐2站到商场。
(2)文文乘坐4路车从动物园上车,向西南方向坐1站到幸福路,再向西面坐2站到天文馆,最后向西北方向坐1站到商场。
故答案为:(1)东北;1;东;2;(2)西南;西;2;西北方向;1。
【分析】描述路线图时,要先按行走路线确定每一个观测点,然后以每一个观测点为参照物,描述到下一个目标所行走的方向和距离。
41.(1)解:60×25=1500(平方米)
答:游泳池的占地面积是1500平方米。
(2)解:60×25+60×2×2+25×2×2
=1500+240+100
=1840(平方米)
答:抹水泥面积是1840平方米。
(3)解:60×2+25×2
=120+50
=170(米)
答:水位线全长170米。
【解析】(1)要求游泳池的占地面积,用长×宽=长方体的占地面积,据此列式解答;
(2)要求在游泳池底面和内壁抹一层水泥,抹水泥面积是多少平方米,就是求无盖长方体的表面积,用公式:无盖长方体的表面积=长×宽+长×高×2+宽×高×2,据此列式解答;
(3) 沿游泳池的内壁1.5米高处用白漆画一条水位线,要求水位线的长度,就是求两条长与两条宽的长度之和,据此列式解答.
42.解:2×=(千克)
2×=(千克)
答:含蛋白质千克,碳水化合物千克。
【解析】根据题意可知,黄豆的总质量×蛋白质约占总质量的分率=蛋白质的质量, 黄豆的总质量×碳水化合物约占总质量的分率=碳水化合物的质量,据此列式解答。
43.解:设收集易拉罐x个,则收集塑料瓶2.5x个。
x+2.5x=210
3.5x=210
x=210÷3.5
x=60
2.5×60=150(个)
答:收集易拉罐60个,则收集塑料瓶150个。
【解析】等量关系:收集易拉罐个数+收集塑料瓶个数=210个,根据等量关系列方程,根据等式性质解方程。
44.解:64×4×4
=16×4
=64(平方分米)
答:至少需要64平方分米的铁皮。
【解析】正方体的表面积=棱长×棱长×6,本题中由于是通风管,则缺少两个面,所以铁皮的面积=棱长×棱长×4,代入数值计算即可。
45.解:设每分钟漏进x桶水。
25x+450=30×25
25x+450=750
25x=300
x=12
答:每分漏进12桶水。
【解析】本题可以设每分钟漏进x桶水,题中存在的等量关系是:每分钟漏进水的桶数×抽完用的时间+已经漏进的桶数=抽水机每分抽水的桶数×抽完用的时间,据此代入字母和数据作答即可。
46.解: ÷ = (g)
答:一个成年人一天需要 g钙。
【解析】一个成年人一天需要钙质的克数=一杯鲜牛奶含有钙质的克数÷一杯鲜牛奶含有钙质的克数占一个成年人一天所需钙质的几分之几,据此代入数据作答即可。
47.解:设经过x小时两车相遇。
(42+38)×x=400
80x=400
80x÷80=400÷80
x=5
答:经过5小时两车相遇。
【解析】此题主要考查了列方程解决相遇应用题,设经过x小时两车相遇,(甲车的速度+乙车的速度)×相遇时间=总路程,据此列方程解答。
48.解:400×40=16000(cm3)
40×40×(40-35)
=1600×5
=8000(cm3)
16000-8000=8000(cm3)=8(dm3)=8(L)
答:会溢出8升的水。
【解析】长方体铁棒放在容器中的体积=铁棒的横截面积×铁棒的长度,水面以上空间的体积=正方体容器的棱长×正方体容器的棱长×原来水面以上的高度,所以溢出水的体积=长方体铁棒放在容器中的体积-水面以上空间的体积。
49.解:(20×15+20×4)×2+15×4
=(300+80)×2+15×4
=380×2+15×4
=760+60
=820(平方厘米)
答:至少要820平方厘米的硬纸板。
【解析】至少要硬纸板的面积=(长×宽+长×高)×2+宽×高。
50.解:×3.14×42×3÷(5×2)
=×3.14×16×3÷10
=50.24÷10
=5.024(米)
答:这些稻谷铺平能有5.024米。
【解析】这些稻谷铺平后的高度=×π×半径2×圆锥的高÷(长方体粮仓的长×宽)。
21世纪教育网(www.21cnjy.com)
同课章节目录
