八下期末压轴专题：过对称中心的折叠问题

中小学教育资源及组卷应用平台
过对称中心的折叠问题
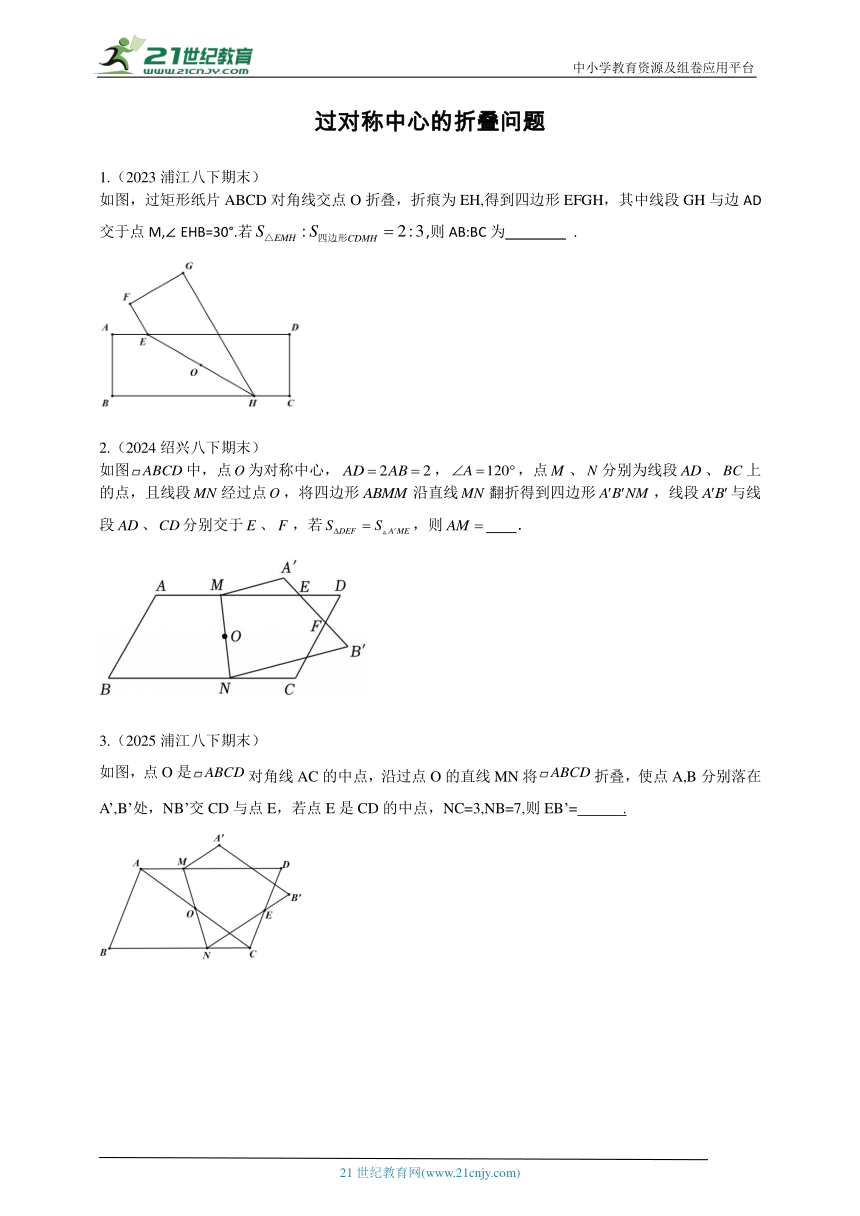
1.（2023浦江八下期末）
如图，过矩形纸片ABCD对角线交点O折叠，折痕为EH,得到四边形EFGH，其中线段GH与边AD交于点M,∠EHB=30°.若,则AB:BC为 .
2.（2024绍兴八下期末）
如图中，点为对称中心，，，点、分别为线段、上的点，且线段经过点，将四边形沿直线翻折得到四边形，线段与线段、分别交于、，若，则　　．
3.（2025浦江八下期末）
如图，点O是对角线AC的中点，沿过点O的直线MN将折叠，使点A,B分别落在A’,B’处，NB’交CD与点E，若点E是CD的中点，NC=3,NB=7,则EB’= .
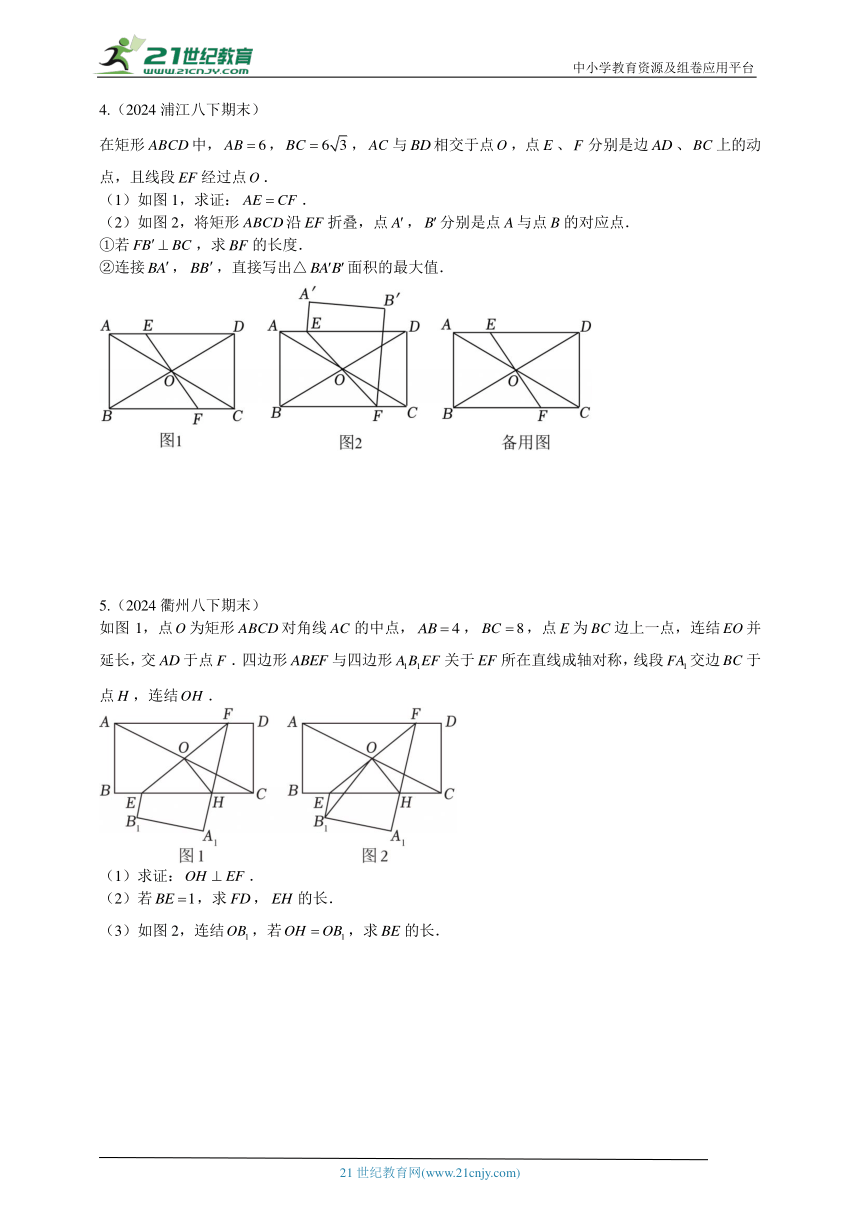
4.（2024浦江八下期末）
在矩形中，，，与相交于点，点、分别是边、上的动点，且线段经过点．
（1）如图1，求证：．
（2）如图2，将矩形沿折叠，点，分别是点与点的对应点．
①若，求的长度．
②连接，，直接写出△面积的最大值．
5.（2024衢州八下期末）
如图1，点为矩形对角线的中点，，，点为边上一点，连结并延长，交于点．四边形与四边形关于所在直线成轴对称，线段交边于点，连结．
（1）求证：．
（2）若，求，的长．
（3）如图2，连结，若，求的长．
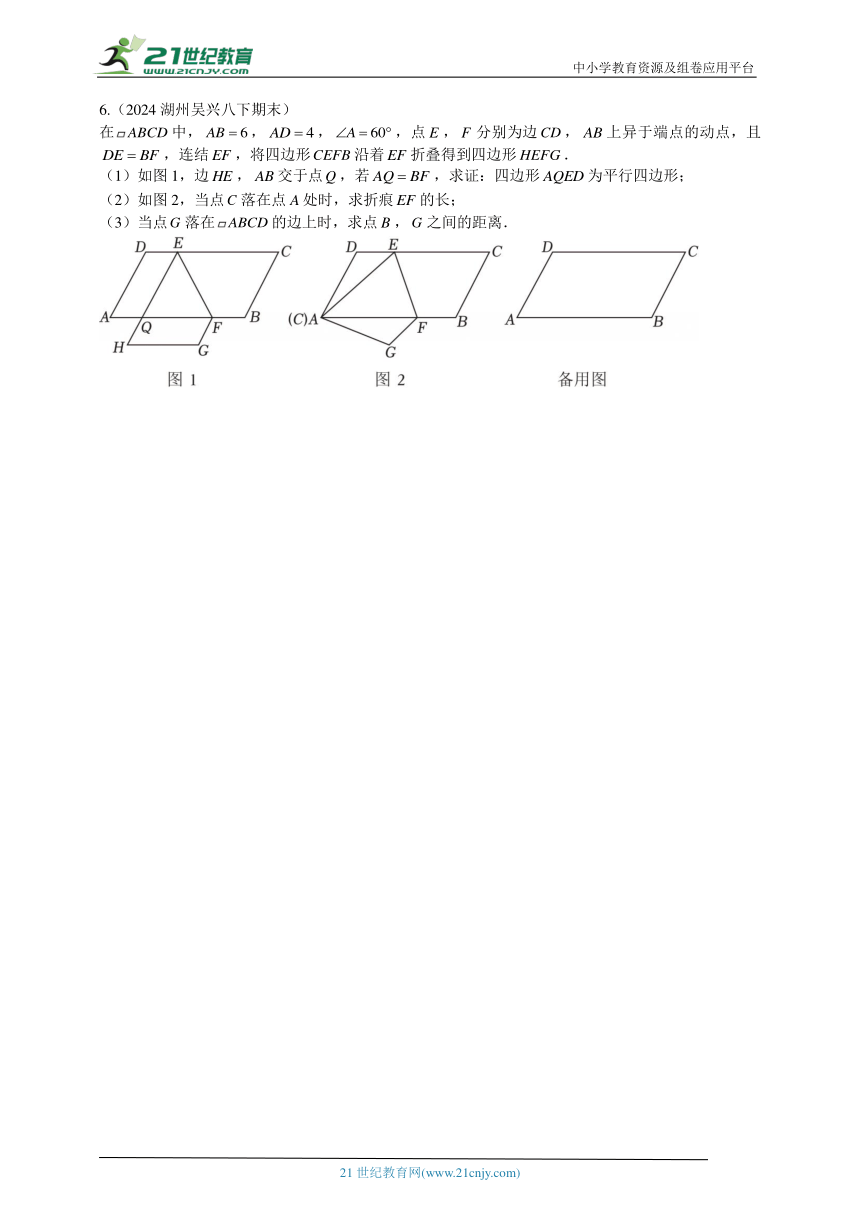
6.（2024湖州吴兴八下期末）
在中，，，，点，分别为边，上异于端点的动点，且，连结，将四边形沿着折叠得到四边形．
（1）如图1，边，交于点，若，求证：四边形为平行四边形；
（2）如图2，当点落在点处时，求折痕的长；
（3）当点落在的边上时，求点，之间的距离．
参考答案：
3.
（1）证明：矩形，，为对角线，
，，
，，
，
；
（2）解：①当在上方和在下方两种情况讨论，
如图，当在上方时，作交于点，
矩形，，，由勾股定理可得，
，是等边三角形，
，
由折叠可知，，，
当在下方时，如图，
同理可得，故 时，；
②，
理由：如图，连接，过点作于点，过点作于点，
由折叠可知，，最大时，△的面积最大，
在点、运动过程中，不变，不变，
由图可知，，由①可知，，△为等边三角形，
，，当与重合时，，
△面积的最大值为：．
4. 2
5.（1）证明：如图1，
是矩形，，．
点为矩形对角线的中点，，
又，．，
为的中点．
四边形与四边形关于所在直线成轴对称，
，．，
又为的中点．；
（2）解：由（1）得，
，
四边形是矩形，
，
，
设，则，．
过点作垂直，如图2，
则四边形为矩形，
，，
．
在中，，
即，解得，．
（3）解：由对称得，
点为矩形对角线的中点，
，
若，则，
当点，，重合满足条件，
连结，如图3，
，，，
△，
，，
与共线，
点、点和点三点共线，
，，，
△，
，
设，则，
在中．
即，
解得，
即．
6.（1）证明：，，
，
在平行四边形中，，
四边形为平行四边形；
（2）解：过点作的垂线，交延长线于点，连结，交于点，如图，
由轴对称性可知：垂直平分，
，
在△中，
，
，
，．
由勾股定理得：，
．
在△中，
由勾股定理得：，
设，则，，
，
解得：，
，
，
由平行四边形的中心对称性，得．
折痕的长为．
（3）解：①当点落在边上时，如图，
由折叠性质可知：，，，
，
，
在平行四边形中，
，
四边形是平行四边形，
，
在△中，
，
，
．
②当点落在边上时，连结交于点，连接，如图，
由平行四边形的中心对称性，得，
由翻折的性质得：
，
△为直角三角形，，
；
③当点落在边上时，连结交于点，如图，
由折叠可知：，
，
．
则垂直平分，
由轴对称性可知垂直平分，
点与点重合．
过点作的垂线交于点，
在△中，
，，
，
由勾股定理，得．
综上所述，点，之间的距离为4或或．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)