河北省平泉县第四中学人教版九年级数学上册课件:24.4 圆锥的侧面积与全面积 (共28张PPT)
文档属性
| 名称 | 河北省平泉县第四中学人教版九年级数学上册课件:24.4 圆锥的侧面积与全面积 (共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 963.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-01 00:00:00 | ||
图片预览







文档简介
课件28张PPT。 圆锥的侧面积全面积1.半径为6,圆心角为60°的扇形的弧长等于 ,面积等于 .
2.已知扇形的圆心角为120°,弧长为20π,扇形的面积为__ .知识再现认识圆锥圆锥知多少1.圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面. 2.把圆锥底面圆周上的
任意一点与圆锥顶点的
连线段叫做圆锥的母线 圆锥的再认识A1A2问题:
圆锥的母线有几条? 3.连结顶点与底面圆心
的线段叫做圆锥的高 如图中 是圆锥的一条母线,
而h就是圆锥的高 4.圆锥的底面半径、
高线、母线长三者之间
间的关系: 根据下列条件求值(其中r、h、 分别是圆锥的底面半径、高线、母线长)
(1) = 2,r=1 则 h=_______
(2) h =3, r=4 则 =_______
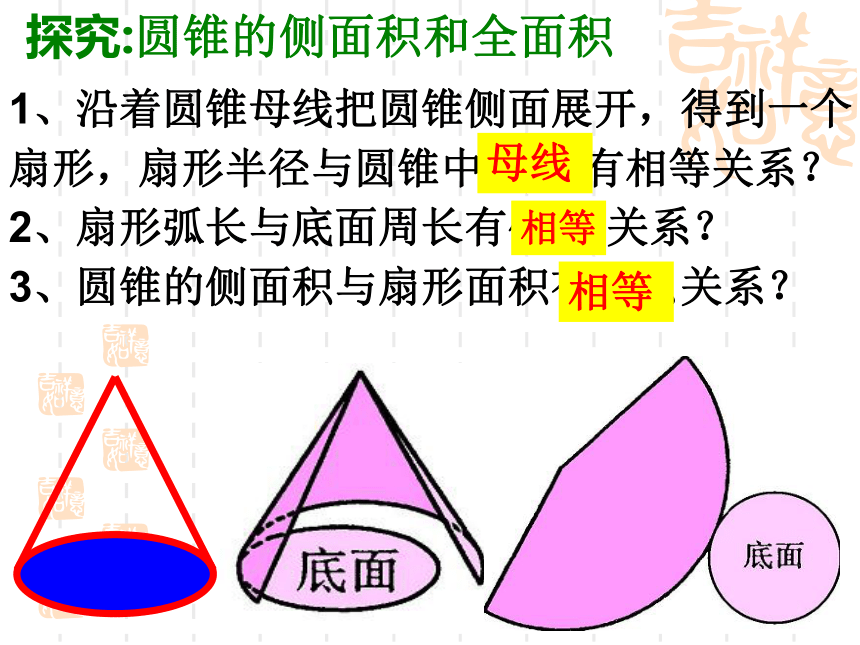
(3) = 10, h = 8 则r=_______56r、h、 三基本元素互求抢答:看谁快!1、沿着圆锥母线把圆锥侧面展开,得到一个扇形,扇形半径与圆锥中什么 有相等关系?
2、扇形弧长与底面周长有什么 关系?
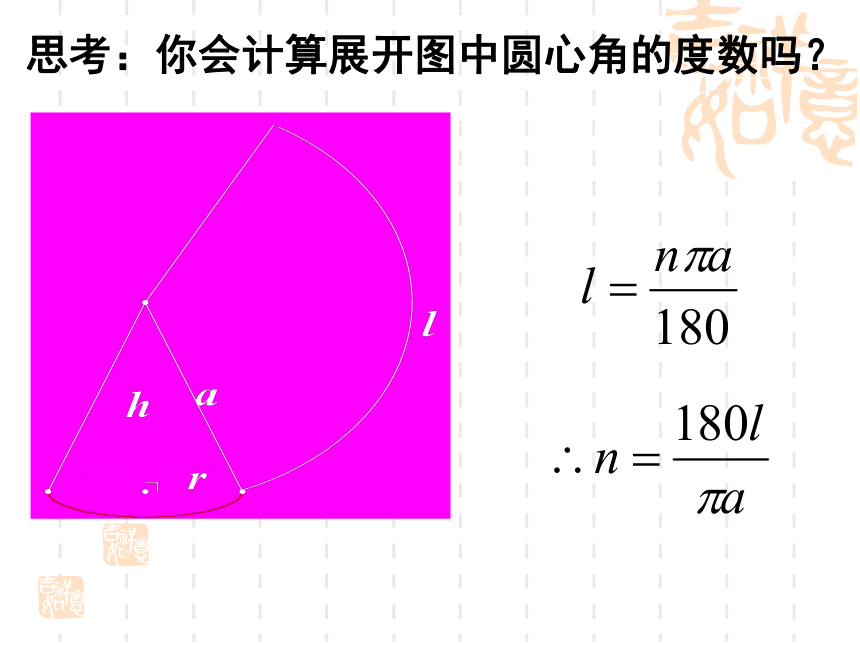
3、圆锥的侧面积与扇形面积有什么关系?相等母线探究:圆锥的侧面积和全面积相等 圆锥的侧面积和全面积 圆锥侧面积就是弧长为圆锥底面周 长、半径为圆锥一条母线长的扇形面积. 圆锥全面积=圆锥侧面积+底面积.思考:你会计算展开图中圆心角的度数吗?填空:(θ 、R为圆锥侧面积展开图扇形圆心角、半径.r、 分别是圆锥底面半径、母线长)
1) = 2,r = 1 则θ=___
2)θ=90°,r=4则 =_____
θ、 r、 三基本元素互求RR例题讲解例1:制作如图所示圆锥形铁皮烟囱帽,其尺寸要求为:底面直径80cm,母线长50cm,求烟囱帽铁皮的面积 变:若圆锥形铁皮烟囱的高为40,底面半径为30,你能求烟囱帽的侧面积吗? 1. 已知圆锥的母线长为2cm,底面半径为1cm,则圆锥的侧面积 .
全面积 .
追踪练习 2. 已知圆锥的母线长为5cm,高为3cm,则圆锥的侧面积 .全面积 .
例2、如图,在扇形中,半径R=10,圆心角θ=120°,用这个扇形围成一个圆锥的侧面.(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高
?
Rhr1.扇形半径为30,圆心角为120°,用它做一个圆锥模型侧面,求这个圆锥底面半径和高.
2.圆锥的侧面展开图是一个半圆,求这个圆锥的母线长与底面半径之比.
3.已知圆锥的母线长为2cm,底面半径为1cm,求圆锥的侧面展开图中扇形的圆心角.
追踪练习 如图,圆锥底面半径为1,母线长6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行最短路线是多少?61B’解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°连接BB’,即为蚂蚁爬行的最短路线拓展延伸:变式:如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少? 已知:在RtΔABC,
求以AB为轴旋转一周所得到的几何体的全面积。BCA拓展延伸: 一个直角三角形的两直角边分别是15cm和20cm,以它的斜边为旋转轴旋转这个三角形,便形成一个旋转体,求这个旋转体的表面积(结果保留π).
追踪练习1、如图,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成一个圆锥模型,设圆的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为 ( )
A.R=2r B.
C.R=3r D.R=4rD巩 固 练 习2、若一个圆锥的底面半径为3,母线长为5,则它的侧面展开图的圆心角是( )
A.60° B.90°
C.120° D.216°D3、如图,圆柱的轴截面ABCD是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短路径长为 ( )A.2 B.2
C.4 D.2
B4、李明同学和马强同学合作,将半径为1米,圆心角为90°的扇形薄铁板围成一个圆锥筒.在计算圆锥的容积(接缝忽略不计)时,李明认为圆锥的高就等于扇形的圆心O到弦AB的距离OC(如图),马强说这样计算不正确,你同意谁的说法?说说你的理由。例4.童心玩具厂欲生产一种圣诞老人的帽子,其圆锥形帽身的母线长为15cm,底面半 径为5cm,生产这种帽身10000个,你 能帮玩具厂算一算至少需多少平方 米的材料吗(不计接缝用料和余料, π取3.14 )?练习1.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.
2.一个圆柱形水池的底面半径为5m,池深1.5m.要在池的内壁和底面涂上油漆,求总计要涂油漆的面积.
3.一种纸帽的底面周长为58cm,高为20cm,要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0.1cm)
课堂练习 练习.一个圆锥形轴截面是一个等边三角形,圆锥的底面半径是6,求圆锥的高线长。 圆柱侧面展开图圆柱的侧面展开图是一个矩形,它的一边长是圆柱的高;它的另一边长是圆柱的底面圆周长 你能找出圆锥及侧面展开图的相关不变量吗?圆柱的侧面积=圆柱的高×底面圆周长 圆柱的全面积=侧面积+两个底面积 练习.一个圆锥形轴截面是顶角450的三角形, 母线长2,求圆锥的底面积。
2.已知扇形的圆心角为120°,弧长为20π,扇形的面积为__ .知识再现认识圆锥圆锥知多少1.圆锥是由一个底面和一个侧面围成的,它的底面是一个圆,侧面是一个曲面. 2.把圆锥底面圆周上的
任意一点与圆锥顶点的
连线段叫做圆锥的母线 圆锥的再认识A1A2问题:
圆锥的母线有几条? 3.连结顶点与底面圆心
的线段叫做圆锥的高 如图中 是圆锥的一条母线,
而h就是圆锥的高 4.圆锥的底面半径、
高线、母线长三者之间
间的关系: 根据下列条件求值(其中r、h、 分别是圆锥的底面半径、高线、母线长)
(1) = 2,r=1 则 h=_______
(2) h =3, r=4 则 =_______
(3) = 10, h = 8 则r=_______56r、h、 三基本元素互求抢答:看谁快!1、沿着圆锥母线把圆锥侧面展开,得到一个扇形,扇形半径与圆锥中什么 有相等关系?
2、扇形弧长与底面周长有什么 关系?
3、圆锥的侧面积与扇形面积有什么关系?相等母线探究:圆锥的侧面积和全面积相等 圆锥的侧面积和全面积 圆锥侧面积就是弧长为圆锥底面周 长、半径为圆锥一条母线长的扇形面积. 圆锥全面积=圆锥侧面积+底面积.思考:你会计算展开图中圆心角的度数吗?填空:(θ 、R为圆锥侧面积展开图扇形圆心角、半径.r、 分别是圆锥底面半径、母线长)
1) = 2,r = 1 则θ=___
2)θ=90°,r=4则 =_____
θ、 r、 三基本元素互求RR例题讲解例1:制作如图所示圆锥形铁皮烟囱帽,其尺寸要求为:底面直径80cm,母线长50cm,求烟囱帽铁皮的面积 变:若圆锥形铁皮烟囱的高为40,底面半径为30,你能求烟囱帽的侧面积吗? 1. 已知圆锥的母线长为2cm,底面半径为1cm,则圆锥的侧面积 .
全面积 .
追踪练习 2. 已知圆锥的母线长为5cm,高为3cm,则圆锥的侧面积 .全面积 .
例2、如图,在扇形中,半径R=10,圆心角θ=120°,用这个扇形围成一个圆锥的侧面.(1)求这个圆锥的底面半径r;
(2)求这个圆锥的高
?
Rhr1.扇形半径为30,圆心角为120°,用它做一个圆锥模型侧面,求这个圆锥底面半径和高.
2.圆锥的侧面展开图是一个半圆,求这个圆锥的母线长与底面半径之比.
3.已知圆锥的母线长为2cm,底面半径为1cm,求圆锥的侧面展开图中扇形的圆心角.
追踪练习 如图,圆锥底面半径为1,母线长6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行最短路线是多少?61B’解:设圆锥的侧面展开图为扇形ABB’, ∠BAB’=n°连接BB’,即为蚂蚁爬行的最短路线拓展延伸:变式:如图,圆锥的底面半径为1,母线长为3,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上,问它爬行的最短路线是多少? 已知:在RtΔABC,
求以AB为轴旋转一周所得到的几何体的全面积。BCA拓展延伸: 一个直角三角形的两直角边分别是15cm和20cm,以它的斜边为旋转轴旋转这个三角形,便形成一个旋转体,求这个旋转体的表面积(结果保留π).
追踪练习1、如图,在正方形铁皮上剪下一个圆形和扇形,使之恰好围成一个圆锥模型,设圆的半径为r,扇形半径为R,则圆的半径与扇形半径之间的关系为 ( )
A.R=2r B.
C.R=3r D.R=4rD巩 固 练 习2、若一个圆锥的底面半径为3,母线长为5,则它的侧面展开图的圆心角是( )
A.60° B.90°
C.120° D.216°D3、如图,圆柱的轴截面ABCD是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短路径长为 ( )A.2 B.2
C.4 D.2
B4、李明同学和马强同学合作,将半径为1米,圆心角为90°的扇形薄铁板围成一个圆锥筒.在计算圆锥的容积(接缝忽略不计)时,李明认为圆锥的高就等于扇形的圆心O到弦AB的距离OC(如图),马强说这样计算不正确,你同意谁的说法?说说你的理由。例4.童心玩具厂欲生产一种圣诞老人的帽子,其圆锥形帽身的母线长为15cm,底面半 径为5cm,生产这种帽身10000个,你 能帮玩具厂算一算至少需多少平方 米的材料吗(不计接缝用料和余料, π取3.14 )?练习1.圆锥的底面直径为80cm.母线长为90cm,求它的全面积.
2.一个圆柱形水池的底面半径为5m,池深1.5m.要在池的内壁和底面涂上油漆,求总计要涂油漆的面积.
3.一种纸帽的底面周长为58cm,高为20cm,要制作20顶这样的纸帽至少要用多少平方厘米的纸?(结果精确到0.1cm)
课堂练习 练习.一个圆锥形轴截面是一个等边三角形,圆锥的底面半径是6,求圆锥的高线长。 圆柱侧面展开图圆柱的侧面展开图是一个矩形,它的一边长是圆柱的高;它的另一边长是圆柱的底面圆周长 你能找出圆锥及侧面展开图的相关不变量吗?圆柱的侧面积=圆柱的高×底面圆周长 圆柱的全面积=侧面积+两个底面积 练习.一个圆锥形轴截面是顶角450的三角形, 母线长2,求圆锥的底面积。
同课章节目录
