河北省平泉县第四中学人教版九年级数学下册课件:27.2.1 相似三角形的判定(第3课时) (共27张PPT)
文档属性
| 名称 | 河北省平泉县第四中学人教版九年级数学下册课件:27.2.1 相似三角形的判定(第3课时) (共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 751.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-01 09:25:16 | ||
图片预览


文档简介
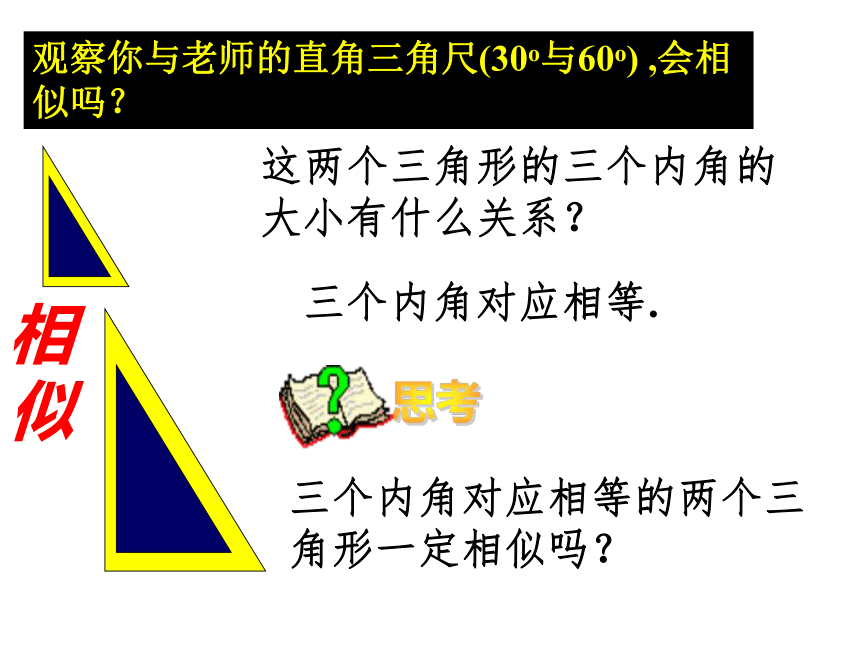
课件27张PPT。第二十七章 相 似相似三角形的判定(第三课时)? 平行于三角形一边的直线与其他两边(或延长线)相交,所构成的三角形与原三角形相似.? 三边对应成比例,两三角形相似.相似三角形的判定方法? 两边对应成比例且夹角相等,两三角形相似.这两个三角形的三个内角的大小有什么关系?三个内角对应相等的两个三角形一定相似吗?三个内角对应相等.观察你与老师的直角三角尺(30o与60o) ,会相似吗?思考相
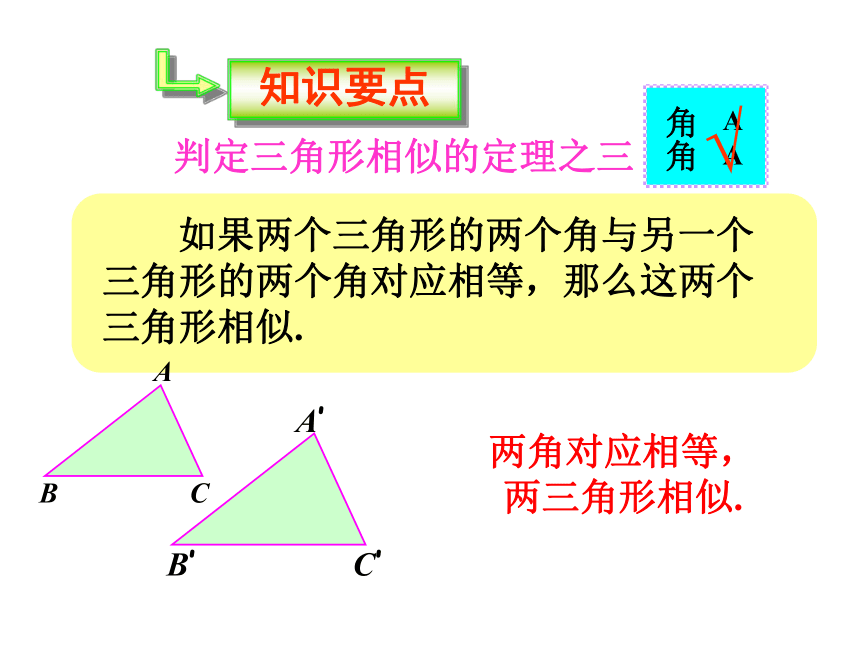
似 如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.判定三角形相似的定理之三两角对应相等,
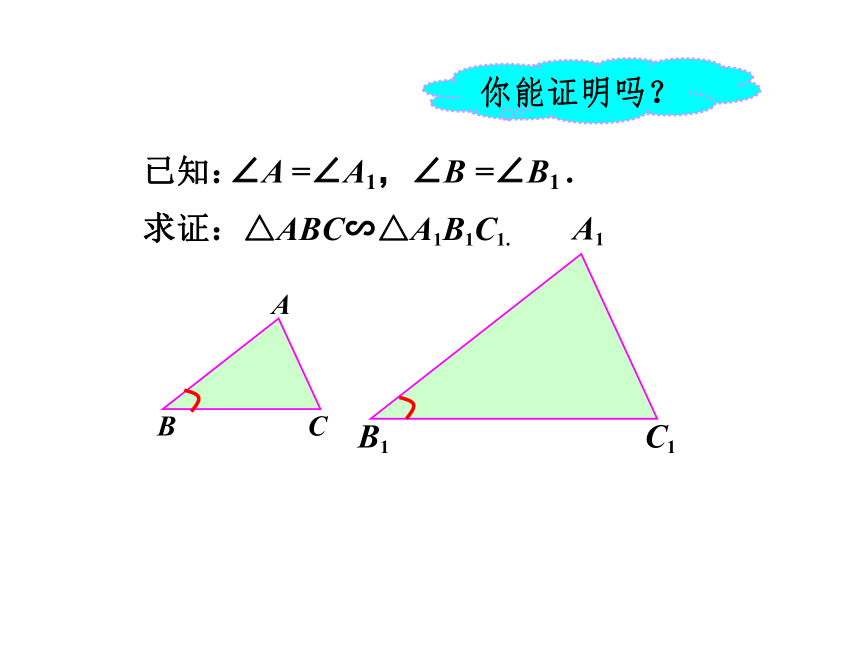
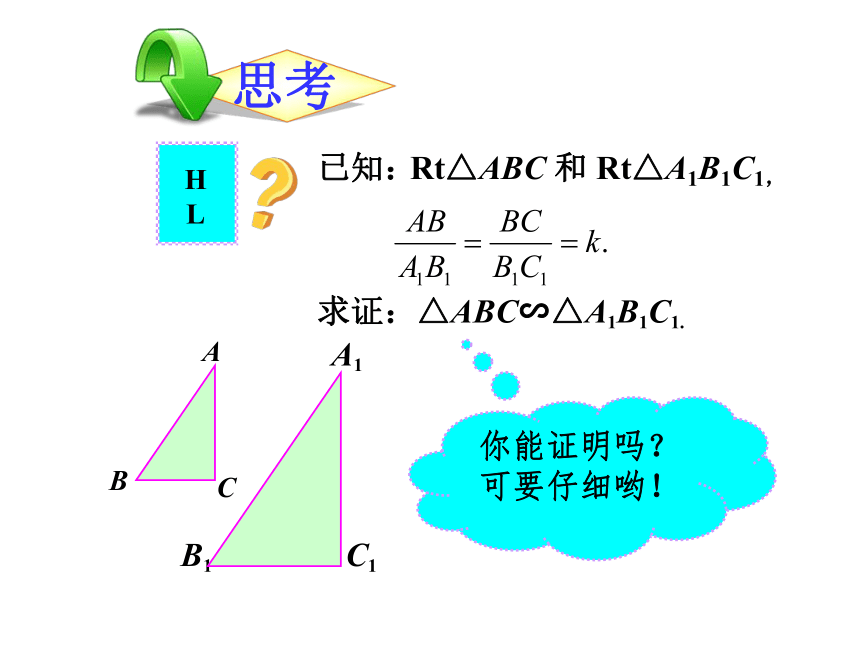
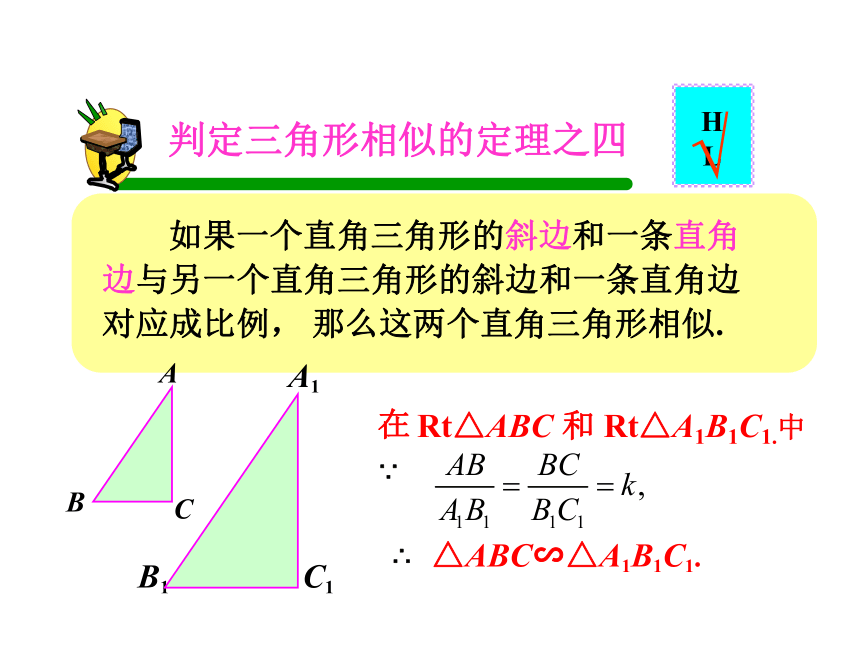
两三角形相似.√已知:△ABC∽△A1B1C1.求证:∠A =∠A1,∠B =∠B1 . 你能证明吗?已知:△ABC∽△A1B1C1.求证:你能证明吗?可要仔细哟!Rt△ABC 和 Rt△A1B1C1, 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.判定三角形相似的定理之四△ABC∽△A1B1C1.在
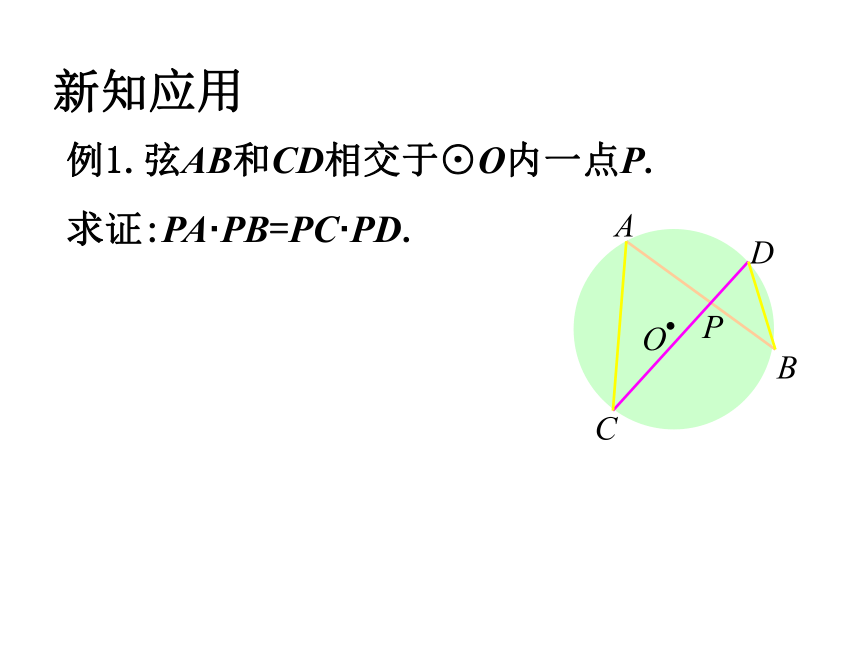
∵∴√Rt△ABC 和 Rt△A1B1C1.中例1.弦AB和CD相交于⊙O内一点P.
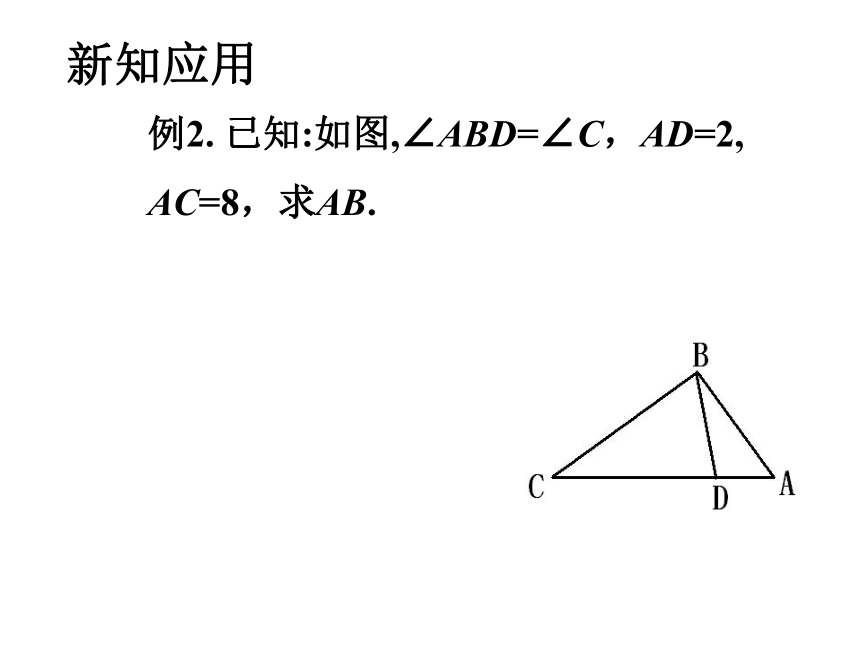
求证:PA·PB=PC·PD.ABCDPO新知应用例2. 已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB. 新知应用例3. 过△ABC(∠C>∠B)的边AB上一点D 作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?CD ●AB在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条? 我们来试一试…课堂小结 相似图形三角形的判定方法: 通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例(三边对应成比例,三角相等)(SSS)(AA)(SAS)(HL)基本图形的形成、变化及发展过程:平行型 斜交型垂直型应用提高1. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 2.填一填
(1)如图3,点D在AB上,当 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
DD3.如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P作直线截ΔABC,使截得的三角形与ΔABC相似,满足这样条件的直线共有 ( )
A.1条 B.2条
C.3条 D.4条画一画4、在△ABC中,∠ACB=90°,CD⊥BA于点D。证明:AC2=AD·AB18 6.已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.7.如图, ∠B=90°,AB=BE=EF=FC=1,求证:
(1) ⊿AEF∽⊿ CEA.
(2) ∠1+ ∠2= 45 °两角分别相等的两个三角形相似AC直角三角形相似的判定
似 如果两个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似.判定三角形相似的定理之三两角对应相等,
两三角形相似.√已知:△ABC∽△A1B1C1.求证:∠A =∠A1,∠B =∠B1 . 你能证明吗?已知:△ABC∽△A1B1C1.求证:你能证明吗?可要仔细哟!Rt△ABC 和 Rt△A1B1C1, 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例, 那么这两个直角三角形相似.判定三角形相似的定理之四△ABC∽△A1B1C1.在
∵∴√Rt△ABC 和 Rt△A1B1C1.中例1.弦AB和CD相交于⊙O内一点P.
求证:PA·PB=PC·PD.ABCDPO新知应用例2. 已知:如图,∠ABD=∠C,AD=2,
AC=8,求AB. 新知应用例3. 过△ABC(∠C>∠B)的边AB上一点D 作一条直线与另一边AC相交,截得的小三角形与△ABC相似,这样的直线有几条?CD ●AB在Rt△ABC的斜边AB上有一点P(点P与点A,B不重合),过点P作直线截得的三角形与△ABC相似,想一想满足条件的直线共有多少条?试画出图形并简要说明理由.思考:若三角形为任意三角形,点P为三角形任意一边上的点,则这样的直线有几条? 我们来试一试…课堂小结 相似图形三角形的判定方法: 通过定义
平行于三角形一边的直线
三边对应成比
两边对应成比例且夹角相等
两角对应相等
两直角三角形的斜边和一条直角边对应成比例(三边对应成比例,三角相等)(SSS)(AA)(SAS)(HL)基本图形的形成、变化及发展过程:平行型 斜交型垂直型应用提高1. 如图,△ABC中,
DE∥BC,EF∥AB,
试说明△ADE∽△EFC. 2.填一填
(1)如图3,点D在AB上,当 时,
△ACD∽△ABC。
(2)如图4,已知点E在AC上,若点D在AB上,则满足
条件 ,就可以使△ADE与原△ABC相似。
DD3.如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P作直线截ΔABC,使截得的三角形与ΔABC相似,满足这样条件的直线共有 ( )
A.1条 B.2条
C.3条 D.4条画一画4、在△ABC中,∠ACB=90°,CD⊥BA于点D。证明:AC2=AD·AB18 6.已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.7.如图, ∠B=90°,AB=BE=EF=FC=1,求证:
(1) ⊿AEF∽⊿ CEA.
(2) ∠1+ ∠2= 45 °两角分别相等的两个三角形相似AC直角三角形相似的判定
