(期末培优卷)期末核心考点突破提升培优卷-2024-2025学年五年级下学期数学西师大版(含答案解析)
文档属性
| 名称 | (期末培优卷)期末核心考点突破提升培优卷-2024-2025学年五年级下学期数学西师大版(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 607.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-28 18:37:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年五年级下册数学期末核心考点突破提升培优卷
一、填空题
1.如下图,王阿姨给客厅长方体茶几的棱贴上防撞条(与地面接触的棱不贴),至少要 dm的防撞条。
2.饭店里运来80袋大米,每天吃a袋,5天后还剩 袋。当a=5时,还剩 袋。
3.三位数75能同时被2,3整除,那么可以是 。
4.(质数与合数)在1~9这九个数中,a、b相邻且都是质数,m、n相邻且都是合数,则a+b+m+n= 。
5.用3个棱长都是4cm的小正方体拼成一个长方体,这个长方体的体积是 cm3,表面积减少了 cm2。
6.用一根长1m的绳子围成一个三角形,一条边长是m,另一条边长是m,第三边长是 m,它是一个 三角形。
7.(最后一个括号里填小数)。
8.如果a÷b=5(a、b都是不等于0的自然数),那么a、b的最大公因数是 ,最小公倍数是 。
9.在括号里填上“>”“<”或“=”。
0.83
10.过冬了,小白兔只储存了180 根胡萝卜制小灰兔只储存了120个大白菜。为了冬天里有萝卜吃,小灰兔用十几个大白菜换了小白兔一些胡萝卜,这时它们储存的食物数量相等,则一个大白菜可以换 根胡萝卜。
11.两个公司的工资待遇
有两个公司贴出了招聘广告,一旦被甲公司聘用,工资待遇为年工资18000元,以后工作每满一年,递增工资2000元.一旦被乙公司聘用,工资待遇为半年工资9000元,以后工作每满半年,递增工资500元.想一想,哪个公司的薪金高呢? (填甲或乙)
12.已知x,y是不同的素数, 且 xy=2x+4y+7, 则x+y= 。
13.李师傅做了有若干个杯子,拿出它的 包装入箱,可装满12箱余60个,把余下的60个与它的 合在一起进行包装,可装满15箱,这批杯子有 个。
二、判断题
14.方程x÷8=7.2与6a-x=51.6的解相同,则a等于18.2。( )
15.因为a>c,所以 ×t>1.( )
16.一个三位数,每个数位上的数字都是a(a不为0),这个三位数一定是3的倍数。( )
17.一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的9倍。( )
180.5a=0不是方程.( )
19.棱长是6dm的正方体的表面积和体积相等。( )
20.两个质数相乘,得到的积一定是合数。( )
21.假分数的倒数一定比1小.( )
22.等式左边加一个数,右边减去同一个数,所得结果仍然是等式.( )
23.a的最大因数和b的最小倍数相等,那么a与b相等。(
)
三、单选题
24.<□< , 在□里填分数, 有( )种填法。
A.3 B.5 C.9 D.无数
25.两个质数相乘,积一定是 ;两个奇数相加,和一定是 。
A.质数 B.合数 C.奇数 D.偶数
A.质数 B.合数 C.奇数 D.偶数
26.用小棒摆a个正方形和b个三角形,共需要用小棒( )根。
A.a+b B.4a+3b C.3a+4b D.4a+b
27.把一个长方体分成几个小正方体后,这些小正方体的表面积之和( )。
A.不变 B.比原来小了 C.比原来大了 D.无法比较
28.棱长为a的两个正方体拼成一个长方体,长方体的表面积比原来减少了( )。
A.4a B.2a C.2a D.4a
29.关于奇数、偶数、质数、合数的讨论,下列说法正确的是( )。
A.所有的质数都是奇数
B.除了 2 以外,任意两个质数的和一定是偶数
C.奇数-奇数=奇数
D.任意两个自然数的积都是合数
30.一种水箱最多可以装4升水,我们就说这种水箱的是( )4升。
A.表面积 B.体积 C.容积 D.重量
31.下面事件适合用下图来表示的是( )
①某冷饮店冰激棱各月的销量。
②某同学一到六年级的身高变化。
③6种不同品牌汽车销售的销量。
④可能表示某位小学生考试成绩的变化。
A.①② B.①③ C.①④ D.②③
32. 与 比较,正确的说法是( )。
A.分数大小相同,分数意义不同
B.分数大小、分数意义都不同
C.分数大小相同, 的分数单位较小
D.分数大小相同, 的分数单位较大
33.专73路和62路公共汽车早6:00同时从公交枢纽首班车发车。专73路车每8分钟发一辆,62 路车每10分钟发一辆。 那么这两路公共汽车第二次同时发车的时间是( )。
A.6:32 B.6:40 C.6:50 D.7:00
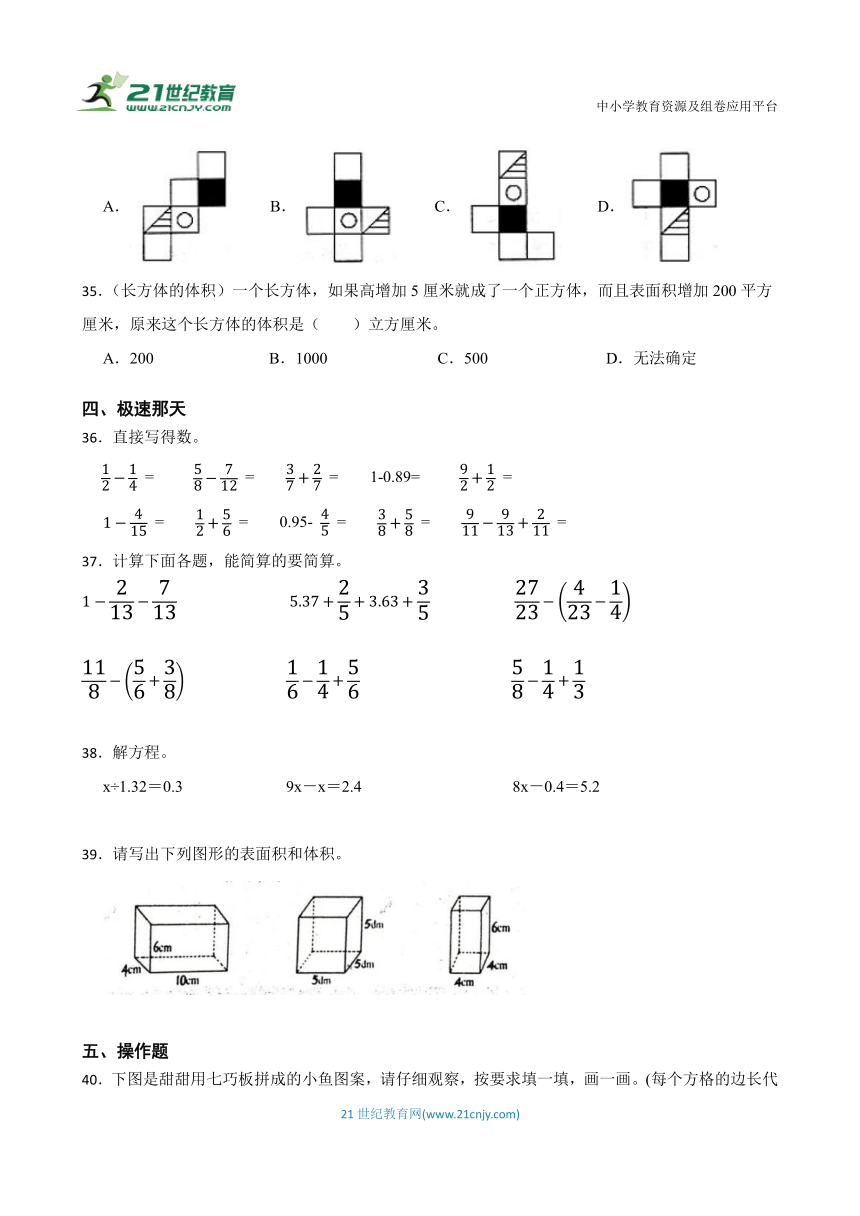
34.把下图中左边正方体的表面展开,得到的展开图是( )。
A. B. C. D.
35.(长方体的体积)一个长方体,如果高增加5厘米就成了一个正方体,而且表面积增加200平方厘米,原来这个长方体的体积是( )立方厘米。
A.200 B.1000 C.500 D.无法确定
四、极速那天
36.直接写得数。
= = = 1-0.89= =
= = 0.95- = = =
37.计算下面各题,能简算的要简算。
38.解方程。
x÷1.32=0.3 9x-x=2.4 8x-0.4=5.2
39.请写出下列图形的表面积和体积。
五、操作题
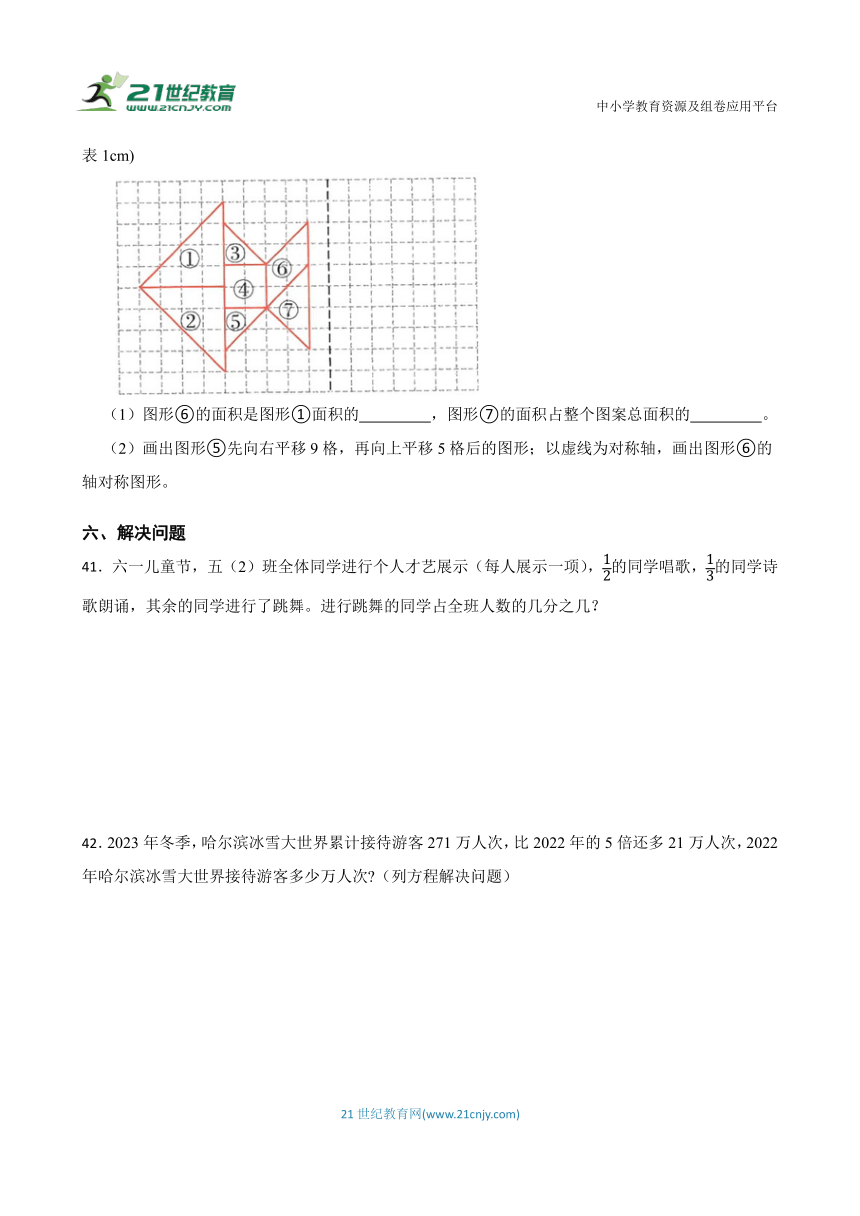
40.下图是甜甜用七巧板拼成的小鱼图案,请仔细观察,按要求填一填,画一画。(每个方格的边长代表1cm)
(1)图形⑥的面积是图形①面积的 ,图形⑦的面积占整个图案总面积的 。
(2)画出图形⑤先向右平移9格,再向上平移5格后的图形;以虚线为对称轴,画出图形⑥的轴对称图形。
六、解决问题
41.六一儿童节,五(2)班全体同学进行个人才艺展示(每人展示一项),的同学唱歌,的同学诗歌朗诵,其余的同学进行了跳舞。进行跳舞的同学占全班人数的几分之几?
42.2023年冬季,哈尔滨冰雪大世界累计接待游客271万人次,比2022年的5倍还多21万人次,2022年哈尔滨冰雪大世界接待游客多少万人次 (列方程解决问题)
43.如图是一个无盖的长方体的展开图,根据这个展开图用玻璃制作一个玻璃容器。
(1)至少需要多少平方分米的玻璃?
(2)在制作好的容器里倒入5L水和体积和为1立方分米的金鱼,容器里水面的高度是多少分米?(容器的厚度忽略不计)
44.一块长30厘米,宽20厘米的长方形铁皮,四个角各切掉一个边长为5厘米的正方形后,做成一个无盖的长方体盒子。做这个盒子用了多少平方厘米铁皮?它的容积是多少立方分米?
45.“火树银花元夕夜,彩灯万盏熠霞流。”为弘扬中华优秀传统文化,元宵节前夕,学校手工社团的同学们做了24盏纱灯和32盏礼花灯,准备参加灯展。把这些灯笼分装到纸箱里,不能混装且每箱的灯笼数量要相等,每箱最多能装几盏灯笼?
46.研学一班有队员48人,研学二班有队员42人。如果把两个班的学生分别分成若干小组,要使两个班每个小组的人数相同,每个小组最多有几人?
47.一辆公交车在始发站上车28人,在文化广场下去a人,又上来b人。
(1)用式子表示现在车上的人数。
(2)当a=9,b=12时,现在车上有多少人?
48.在一根木棍上,有三种刻度线,第一种刻度线将木棍分成10等份;第二种刻度线将木棍分成 12等份:第三种刻度线将木棍分成15等份。如果沿每条刻度线将木锯断,木棍总共被锯成多少段?
49.一个旅游团租车出游,平均每人应付车费40元.后来又增加了8个人,这样每人应付的车费是35元,租车费是多少元?
50.从神舟七号到神舟十八号载人飞船的成功发射,展示了中国载人航天工程在过去十六年中的巨大变化。学校组织五年级8名老师和155名同学前往某航天馆参观,每辆车限载乘客40 人(不算司机),准备出发时发现还剩余3人没有座位。
收费标准 个人票:50元/人(学生半价)
团体票:100人以上(含100人)26元/人
(1)学校一共租了几辆车 (列方程解答)
(2)航天馆的售票方式如图。全员怎样购票更划算
参考答案及试题解析
1.56
【解析】解:12×2+6×2+5×4
=24+12+20
=56(dm)
故答案为:56。
【分析】看图及根据题意可知防撞条由长方体茶几的2条长、2条宽和4条高组成,因此,长×2+宽×2+高×4=至少需要的防撞条长度。
2.80-5a;55
【解析】饭店里运来80袋大米,每天吃a袋,5天后还剩(80-5a)袋。当a=5时,还剩:80-5×5=55(袋)。
故答案为:80-5a;55。
【分析】用每天吃的袋数乘吃的天数求出5天吃的袋数,用总数减去5天吃的袋数表示出还剩的袋数。把a的值带换成5,求出还剩的袋数即可。
3.0或6
【解析】解:设三位数为75M,
则M必须取偶数0,2,4,6,8,
又因为7+5+M=12+M能被3整除,则M只能取0或6。
故答案为:0或6
【分析】一个数能被2整除的条件是其个位数为偶数(即0、2、4、6、8)。
一个数能被3整除的条件是其各个数位上的数字之和能被3整除。
对于三位数75 :
考虑被2整除的条件,这意味着 必须为偶数(0、2、4、6、8)。
考虑被3整除的条件,计算75 的数字之和,即7+5+ 必须能被3整除。
计算数字之和并寻找符合条件的 值:当 =0时,数字之和为7+5+0=12,能被3整除。
当 =2时,数字之和为7+5+2=14,不能被3整除。
当 =4时,数字之和为7+5+4=16,不能被3整除。
当 =6时,数字之和为7+5+6=18,能被3整除。
当 =8时,数字之和为7+5+8=20,不能被3整除。
因此,只有当 =0或 =6时,三位数75 同时满足能被2和3整除的条件。
4.22
【解析】解:在1~9这九个数中,质数有2、3、5、7。其中,只有2和3是相邻的。所以,a=2,b=3。
在1~9这九个数中,合数有4、6、8、9。其中,只有8和9是相邻的。所以,m=8,n=9。
所以,a+b+m+n=2+3+8+9=22。
故答案为:22
【分析】首先,我们需要确定在1~9这九个数中,哪些是质数,哪些是合数。质数是只有1和它本身两个正因数的自然数,而合数则是有其他正因数的自然数。然后,根据题目条件,我们需要找出相邻的质数和相邻的合数。最后,将这些数相加,得到最终的答案。
5.192;64
【解析】解:4×4×4×3
=64×3
=192(cm3)
4×4×4
=16×4
=64(cm2)
故答案为:192;64。
【分析】通过实际操作可知用3个棱长是4cm的小正方体拼成一个长方体,则长方体表面积与原3个正方体表面积的和比较会减少4个接触面的面积和,而长方体的体积等于3个小正方体体积的和,因此,棱长×棱长×棱长=一个小正方体的体积,棱长×棱长×棱长×3=长方体的体积,棱长×棱长=一个接触面的面积,棱长×棱长×4=减少的表面积。
6.;等腰
【解析】解:1--
=-
=(m),
它是一个等腰三角形;
故答案为:;等腰。
【分析】根据题意,已知三角形周长及两条边长,首先计算第三条边的长度,再根据边长关系判断三角形类型。
7.12;18;8;0.75
8.b;a
【解析】解:如果a÷b=5(a、b都是不等于0的自然数),那么a、b的最大公因数是b,最小公倍数是a。
故答案为:b;a。
【分析】一个数是另一个数的倍数,那么较小数就是他们的最大公因数,较大数就是他们的最小公倍数。
9.<;<;>;>
10.3
【解析】解:设小灰兔用x个大白菜换小白兔y根胡萝卜。
120-x+y=(120+180)÷2
120-x+y=150
y-x=30
又因为10为整数,
所以x=15,y=45
y÷x=3
一个大白菜可以换3根胡萝卜。
故答案为:3
【分析】 首先未知数,即1棵白菜可以换多少只胡萝卜。然后,根据题目给出的条件建立一个等式来表示小白兔和小灰兔的粮食数量相等的情况。接下来通过解这个方程来找到未知数的值,即一棵大白菜可以换多少只胡萝卜。
11.乙
【解析】假如工作年限为n年。在甲公司拿的年薪为:18000+2000+2000×1+2000×2+2000×3+···+2000×n
=18000+1000(1+n)n
=18000+500((2+2n)n
在乙公司拿的年薪为:9000+9000+500×1+500×2+500×3+500×4+···+500×2n
=18000+500(1+2n)n
18000+500((2+2n)n>18000+500(1+2n)n
所以在甲公司拿的年薪高。
【分析】把甲的年薪表示出来,把乙方年薪表示出来,然后再比较。
12.22
【解析】解:根据题意,可得
xy=2x+4y+7
xy-2x-4y-7=0
xy-2x-4y+8-8-7=0
(x-4)(y-2)=15
因为15=1×15=3×5
所以,x-4=1,y-2=15或x-4=3,y-2=5
解得,x=5,y=17或x=7,y=7
因为x,y是不同的素数,所以,x=7,y=7不符合,舍去
所以,x=5,y=17
所以,x+y=5+17=22
故答案为:22
【分析】将原等式移项并用十字相乘法进行因式分解,得到(x-4)(y-2)=15。由于x和y是不同的素数,则x-4和y-2也是整数,且只能是1和15或3和5。 解得x=5,y=17,据此即可求解
13.2700
【解析】解:设这批杯子共有x个,则平均每箱有个。
60+x=15×
60+x=
3600+32x=35x-4500
3x=8100
x=8100÷3
x=2700
故答案为:2700。
【分析】依据等量关系式:余下的个数+剩下的分率×杯子的总个数=剩下可以装满的箱数×平均每箱杯子的个数。
14.正确
【解析】
x÷8=7.2
解:x=7.2×8
x=57.6
当x=57.6时,代入方程 6a-x=51.6 ,
即6a-57.6=51.6
解:6a=51.6+57.6
6a=109.2
a=109.2÷6
a=18.2
故答案为:正确。
【分析】根据被除数=商×除数,求出方程x÷8=7.2的解,然后把x的解代入6a-x=51.6,变成6a-57.6=51.6,再根据被减数=差+减数,一个因数=积÷另一个因数即可。
15.错误
【解析】解:因为a>c,当a<0时,则c<0,t<0时,则 ×t<1;
当a<0时,则c<0,t>0时,则 ×t>1;
当c>0时,则a>0,t≤0时,则 ×t<1;
当c>0时,则c>0,t>0时,则 ×t>1;
当a<0时,则c<0,t<0时,则 ×t<1;
故答案为:错误.
【分析】因为a>c,然后考虑a和c的取值及t的取值,进而得出解论.解答此题的关键是,要考虑a和c的取值及t的取值,做出相应的判断.
16.正确
17.错误
【解析】 一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的27倍,原题说法错误。
故答案为:错误。
【分析】 根据正方体的体积公式:V=a3,正方体的棱长扩大到原来的3倍,它的体积扩大3×3×3=27倍,据此判断。
18.错误
【解析】解:这是等式,又含有未知数,是方程,原题说法错误.
故答案为:错误
【分析】含有未知数的等式叫做方程,由此根据方程的意义判断即可.
19.错误
【解析】 表面积和体积不能比较大小,原题说法错误。
故答案为:错误。
【分析】 立体图形的表面积是指组成它的所有面的面积和,而其体积是指它所占空间的大小,所以二者意义不一样,不能比较大小,据此判断。
20.正确
【解析】解:两个质数相乘,得到的积一定是合数,原题说法正确。
故答案为:正确。
【分析】两个质数相乘,得到的积最少有3个因数,所以一定是合数。
21.错误
【解析】解:假分数的倒数小于或等于1,原题说法错误。
故答案为:错误。
【分析】假分数大于或等于1,所以假分数的倒数小于或等于1。
22.错误
【解析】等式左边加一个数,右边减去同一个数,这个数只有是0时,所得结果仍然是等式,其他数都不是等式.
故答案为错误.
【分析】这道题主要考查了等式的基本性质.等式的基本性质:等式的两边同时加上或减去同一个数,同时乘或除以一个非零数,等式仍然成立.
23.正确
【解析】解:a的最大因数是它本身,b的最小倍数是它本身,那么a与b相等。
故答案为:正确。
【分析】一个数的最大因数与最小倍数都等于它本身,所以a与b相等。
24.D
【解析】解:<□< , 在□里填分数, 有无数种填法。
故答案为:D。
【分析】任意两个分数之间有无数个分数,据此解答。
25.B;D
【解析】解:质数×质数=合数;奇数+奇数=偶数。
故答案为:B;D。
【分析】质数是一个大于1的自然数,除了1和它本身以外,不能被其他自然数整除的数;合数是一个大于1的自然数,除了1和它本身以外,还能被其他自然数整除的数;所以当两个质数相乘时,它们的积一定能被这两个质数相乘,它们的积一定是合数。能够被2整除叫做偶数,不能被2整除叫做奇数;两个奇数相加一定能被2整除,所以它们的和一定是偶数。
26.C
【解析】解:4×a+3×b=(4a+3b)(根)。
故答案为:B。
【分析】共需要用小棒的根数=摆一个正方形需要小棒的根数×摆正方形的个数+摆一个三角形需要小棒的根数×摆三角形的个数。
27.C
【解析】解:把一个长方体分成几个小正方体后,这些小正方体的表面积之和比原来大了。
故答案为:C。
【分析】把一个长方体分成几个小正方体后,表面积比原来多了切面的面积,所以这些小正方体的表面积之和比原来大了。
28.C
【解析】解:减少了:a×a×2=2a .
故答案为:C
【分析】把两个正方体拼在一起后会减少两个正方形的面,每个正方形的面积是a×a,由此计算即可.
29.B
【解析】解:A:不是所有的质数都是奇数,原来说法错误;
B:除了 2 以外,任意两个质数的和一定是偶数,原来说法正确;
C:奇数-奇数=偶数,原来说法错误;
D:不是任意两个自然数的积都是合数。原来说法错误。
故答案为:B。
【分析】A:质数是只有1和本身两个因数的数,最小的质数2是偶数,也是所有质数中唯一的偶数;
B:质数中除了2之外都是奇数,两个奇数的和一定是偶数;
C:奇数-奇数=偶数,奇数+奇数=偶数;
D:例如自然数1和3的积就是质数,由此判断即可。
30.C
【解析】解:一种水箱最多可以装4升水,我们就说这种水箱的是容积4升。
故答案为:C。
【分析】容器所能容纳物体的体积就是它的容积。
31.C
【解析】解:下面事件适合用下图来表示的是①④。
故答案为:C。
【分析】①某冷饮店冰激棱各月的销量可以用单式折线统计图表示;
②某同学一到六年级的身高变化,折线趋势不会下降的;
③6种不同品牌汽车销售的销量,要用条形统计图;
④某位小学生考试成绩的变化可以用单式折线统计图表示。
32.A
【解析】解:与比较,分数大小相同,分数的意义不同。
的分数单位是,的分数单位是,因为>,所以的分数单位较大。
故答案为:A。
【分析】与比较大小,先将单位统一,再比较分子的大小。
分数的意义:把单位1平均分成若干份,表示这样一份或几份的数,叫做分数。本题中是将单位1平均分成3份,取其中的2份;是将单位1平均分成9份,取其中的6份。
把单位“1”平均分成若干份取其中的一份的数,叫做分数单位。即分子是1,分母是正整数的分数,又叫单位分数,记为。
33.B
【解析】8=2×2×2,
10=2×5,
8和10的最小公倍数是2×2×2×5=40,
第二次同时发车的时间是6时+40分=6时40分。
故答案为:B。
【分析】此题主要考查了最小公倍数的应用,先将8和10分别分解质因数,然后求出8和10的最小公倍数,最后用首班车发车时间+最小公倍数=第二次同时发车的时刻,据此列式解答。
34.D
【解析】解:A:三角和黑色面不相邻,此选项错误;
B:三角应该在左边。此选项错误;
C:三角和黑色面不相邻,此选项错误;
D:正确。
故答案为:D。
【分析】观察三个面的位置,这三个面是相邻的,根据正方体的特征确定展开图即可。
35.C
【解析】200÷5 =40(厘米)
40÷4=10(厘米) 10-5=5(厘米)
10×10×5=500(立方厘米)
故答案为:C
【分析】
读题可知长方体底面为正方形,通过增加的表面积求出底面周长,(增加表面积为底面周长×增加的高),进而得出底面边长和原长方体的高,最终由体积公式:长×宽×高计算出体积。
36. = = = 1-0.89=0.11 =5
= = 0.95- =0.15 =1 =
【解析】
【分析】同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
37.解:(1)
=
=
(2)
=
=+
=
(3)
=
=
=
(4)
=
=
=1-
=
(5)
=
=
=
(6)
=
=
=
【解析】(1)先将各个减数化成相同分母的分数形式,再根据分数的减法运算规则进行计算。
(2)先将分数转换为小数,再进行加法运算。
(3)先按照运算法则先计算括号内的运算,然后执行括号外的运算。
(4)首先识别表达式中的运算,然后根据分数的性质进行简化,最后完成计算。
(5)先找到一个公共分母,将各分数转换为同分母形式,之后进行加减运算即可得到结果。
(6)本题主要考查异分母分数的加减运算,需要先将异分母分数通过通分变为同分母分数,然后进行加减运算。
38.x=0.396;x=0.3;x=0.7
39.解:(10×4+10×6+6×4)×2
=(40+60+24)×2
=124×2
=248(cm2)
4×6×10
=24×10
=240(cm3)
5×5×6
=25×6
=150(dm2)
5×5×5
=25×5
=125(dm3)
(4×4+4×6+4×6)×2
=(16+24+24)×2
=64×2
=128(cm2)
4×4×6
=16×6
=96(cm3)
【解析】长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积 =长×宽×高;正方体表面积=棱长×棱长×6;正方体体积=棱长×棱长×棱长,据此列式解答。
40.(1);
(2)
【解析】解:(1)图形⑥的面积是2×2=4(cm2), 图形①的面积是4×4÷2=8(cm2), 4÷8=;
图形⑦的面积是4×2÷2=4(cm2), 整个图案的总面积是4×4÷2×2+2×2÷2×2+2×2×2+4×2÷2=32(cm2)
4÷32=
故答案为:(1);。
【分析】(1)平行四边形的面积=底×高,三角形的面积=底×高÷2,正方形的面积=边长×边长,分别求出各图形的面积,要求一个数是另一个数的几分之几,用除法计算;
(2)平移作图的步骤:①找出能表示图形的关键点;②确定平移的方向和距离;③按平移的方向和距离确定关键点平移后的对应点;④按原图的顺序,连接各对应点,据此作图即可;
画轴对称图形的步骤:①点出关键点,找出所有的关键点,即图形中所有线段的端点;②确定关键点到对称轴的距离,关键点离对称轴多远,对称点就离对称轴多远;③点出对称点;④连线,按照给出的一半图形将所有对称点连接成线段。
41.解:1--
=-
=
答:进行跳舞的同学占全班人数的。
【解析】单位1-唱歌的同学占全班人数的几分之几-诗歌朗诵的同学占全班人数的几分之几=跳舞的同学占全班人数的几分之几。
42.解:设2022年哈尔滨冰雪大世界接待游客x万人次。
5x+21=271
5x=271-21
5x=250
x=250÷5
x=50
答:2022年哈尔滨冰雪大世界接待游客50万人次。
【解析】设2022年哈尔滨冰雪大世界接待游客x万人次。 依据等量关系式:2022年哈尔滨冰雪大世界接待游客的人数×5+多的人数=2023年哈尔滨冰雪大世界接待游客的人数,列方程,解方程。
43.(1)21平方分米
(2)1分米
44.500平方厘米;1立方分米
45.解:24和32的最大公因数是8
答:每箱最多能装8盏灯笼。
【解析】因为装箱时,不能混装且每箱的灯笼数量要相等,那么每箱最多能装灯笼的盏数就是24和32的最大公因数,据此作答即可。
46.解:
48和42的最大公因数是:2×3=6
答:每个小组最多有6人。
【解析】每个小组最多的人数=48和42的最大公因数,用短除法求出。
47.(1)解:用式子表示现在车上的人数(28﹣a+b)人。
(2)解:当a=9,b=12时,
28﹣a+b=28﹣9+12=31
答:现在车上有31人。
【解析】(1)现在车上的人数=一辆公交车在始发站上车的人数-在文化广场下去的人数+又上来的人数;
(2)把a=9,b=12代入计算。
48.设木棍的长度为60厘米。
计算每种刻度线的数量:
10等分的每等分长6cm
刻度线数量,10-1=9(条),
12等分的每等分长5cm为
刻度线数量,12-1=11(条),
15等分的为每等分长4cm
刻度线数量,15-1=14(条)。
计算重合的刻度线数量:
第一种与第二种刻度线重合的条数:
6和5的公倍数是30,有1条。
第一种与第三种刻度线重合的条数:
6和4的公倍数是12、24、36、有4条
第二种与第三种刻度线重合的条数:
5和4的公倍数是20,40,有2条。
计算总的刻度线数量:
因此,共有刻度线9+11+14-1-4-2=27(条)。
计算木棍被锯成的段数:
木棍总共被锯成27+1=28(段)
答: 木棍总共被锯成28段。
【解析】首先,设木棍的长度为60厘米(这是10、12和15的最小公倍数,以便于计算)。然后,计算每种刻度线的数量。接着,找出哪些刻度线是重合的,并计算重合的刻度线数量。最后,计算总的刻度线数量,并据此得出木棍被锯成的段数。
49.解:设原来的乘车人数是x人, 40x=35(x+8) 40x=35x+28040x﹣35x=35x+280﹣35x 5x=280 x=5640×56=2240(元)答:租车费是2240元。
【解析】根据人数增加前后的车费不变找等量关系,等量关系:原来人数×每人应付的钱数=增加后的人数×增加后每人应付的钱数,根据等量关系列方程,解方程。
50.(1)解:设一共租了x辆车。
40x+3=8+155
40x+3=163
40x+3-3=163-3
40x=160
40x÷40=160÷40
x=4
答:学校一共租了4辆车。
(2)解:全员购买个人票
50÷2=25(元),
8×50+155×25=4275(元),
全员购买团体票:
(8+155)×26=4238(元),
8名老师和92名学生购买团体票,剩余63名学生购买个人票:100×26+63×25=4175(元),因为4175<4238<4275,
所以8名老师和92名学生购买团体票,剩下63 名学生买个人票更划算,
答:8名老师和92 名学生购买团体票,剩下63名学生买个人票更划算。
【解析】(1) 还剩余3人没有座位 ,说明师生总数比座位数多3,即座位数+3=师生总数。设一共租了x辆车,座位数40X,师生总数155+8.据此列出方程求解。
(2)分三种情况讨论:1、全员购买个人票;2、全员购买团体票;8名教师和92名学生买团体票,剩下学生买个人票(半价)。分别计算出三种购票方式所需要的钱数,然后作比较那种方式划算。
21世纪教育网(www.21cnjy.com)
2024-2025学年五年级下册数学期末核心考点突破提升培优卷
一、填空题
1.如下图,王阿姨给客厅长方体茶几的棱贴上防撞条(与地面接触的棱不贴),至少要 dm的防撞条。
2.饭店里运来80袋大米,每天吃a袋,5天后还剩 袋。当a=5时,还剩 袋。
3.三位数75能同时被2,3整除,那么可以是 。
4.(质数与合数)在1~9这九个数中,a、b相邻且都是质数,m、n相邻且都是合数,则a+b+m+n= 。
5.用3个棱长都是4cm的小正方体拼成一个长方体,这个长方体的体积是 cm3,表面积减少了 cm2。
6.用一根长1m的绳子围成一个三角形,一条边长是m,另一条边长是m,第三边长是 m,它是一个 三角形。
7.(最后一个括号里填小数)。
8.如果a÷b=5(a、b都是不等于0的自然数),那么a、b的最大公因数是 ,最小公倍数是 。
9.在括号里填上“>”“<”或“=”。
0.83
10.过冬了,小白兔只储存了180 根胡萝卜制小灰兔只储存了120个大白菜。为了冬天里有萝卜吃,小灰兔用十几个大白菜换了小白兔一些胡萝卜,这时它们储存的食物数量相等,则一个大白菜可以换 根胡萝卜。
11.两个公司的工资待遇
有两个公司贴出了招聘广告,一旦被甲公司聘用,工资待遇为年工资18000元,以后工作每满一年,递增工资2000元.一旦被乙公司聘用,工资待遇为半年工资9000元,以后工作每满半年,递增工资500元.想一想,哪个公司的薪金高呢? (填甲或乙)
12.已知x,y是不同的素数, 且 xy=2x+4y+7, 则x+y= 。
13.李师傅做了有若干个杯子,拿出它的 包装入箱,可装满12箱余60个,把余下的60个与它的 合在一起进行包装,可装满15箱,这批杯子有 个。
二、判断题
14.方程x÷8=7.2与6a-x=51.6的解相同,则a等于18.2。( )
15.因为a>c,所以 ×t>1.( )
16.一个三位数,每个数位上的数字都是a(a不为0),这个三位数一定是3的倍数。( )
17.一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的9倍。( )
180.5a=0不是方程.( )
19.棱长是6dm的正方体的表面积和体积相等。( )
20.两个质数相乘,得到的积一定是合数。( )
21.假分数的倒数一定比1小.( )
22.等式左边加一个数,右边减去同一个数,所得结果仍然是等式.( )
23.a的最大因数和b的最小倍数相等,那么a与b相等。(
)
三、单选题
24.<□< , 在□里填分数, 有( )种填法。
A.3 B.5 C.9 D.无数
25.两个质数相乘,积一定是 ;两个奇数相加,和一定是 。
A.质数 B.合数 C.奇数 D.偶数
A.质数 B.合数 C.奇数 D.偶数
26.用小棒摆a个正方形和b个三角形,共需要用小棒( )根。
A.a+b B.4a+3b C.3a+4b D.4a+b
27.把一个长方体分成几个小正方体后,这些小正方体的表面积之和( )。
A.不变 B.比原来小了 C.比原来大了 D.无法比较
28.棱长为a的两个正方体拼成一个长方体,长方体的表面积比原来减少了( )。
A.4a B.2a C.2a D.4a
29.关于奇数、偶数、质数、合数的讨论,下列说法正确的是( )。
A.所有的质数都是奇数
B.除了 2 以外,任意两个质数的和一定是偶数
C.奇数-奇数=奇数
D.任意两个自然数的积都是合数
30.一种水箱最多可以装4升水,我们就说这种水箱的是( )4升。
A.表面积 B.体积 C.容积 D.重量
31.下面事件适合用下图来表示的是( )
①某冷饮店冰激棱各月的销量。
②某同学一到六年级的身高变化。
③6种不同品牌汽车销售的销量。
④可能表示某位小学生考试成绩的变化。
A.①② B.①③ C.①④ D.②③
32. 与 比较,正确的说法是( )。
A.分数大小相同,分数意义不同
B.分数大小、分数意义都不同
C.分数大小相同, 的分数单位较小
D.分数大小相同, 的分数单位较大
33.专73路和62路公共汽车早6:00同时从公交枢纽首班车发车。专73路车每8分钟发一辆,62 路车每10分钟发一辆。 那么这两路公共汽车第二次同时发车的时间是( )。
A.6:32 B.6:40 C.6:50 D.7:00
34.把下图中左边正方体的表面展开,得到的展开图是( )。
A. B. C. D.
35.(长方体的体积)一个长方体,如果高增加5厘米就成了一个正方体,而且表面积增加200平方厘米,原来这个长方体的体积是( )立方厘米。
A.200 B.1000 C.500 D.无法确定
四、极速那天
36.直接写得数。
= = = 1-0.89= =
= = 0.95- = = =
37.计算下面各题,能简算的要简算。
38.解方程。
x÷1.32=0.3 9x-x=2.4 8x-0.4=5.2
39.请写出下列图形的表面积和体积。
五、操作题
40.下图是甜甜用七巧板拼成的小鱼图案,请仔细观察,按要求填一填,画一画。(每个方格的边长代表1cm)
(1)图形⑥的面积是图形①面积的 ,图形⑦的面积占整个图案总面积的 。
(2)画出图形⑤先向右平移9格,再向上平移5格后的图形;以虚线为对称轴,画出图形⑥的轴对称图形。
六、解决问题
41.六一儿童节,五(2)班全体同学进行个人才艺展示(每人展示一项),的同学唱歌,的同学诗歌朗诵,其余的同学进行了跳舞。进行跳舞的同学占全班人数的几分之几?
42.2023年冬季,哈尔滨冰雪大世界累计接待游客271万人次,比2022年的5倍还多21万人次,2022年哈尔滨冰雪大世界接待游客多少万人次 (列方程解决问题)
43.如图是一个无盖的长方体的展开图,根据这个展开图用玻璃制作一个玻璃容器。
(1)至少需要多少平方分米的玻璃?
(2)在制作好的容器里倒入5L水和体积和为1立方分米的金鱼,容器里水面的高度是多少分米?(容器的厚度忽略不计)
44.一块长30厘米,宽20厘米的长方形铁皮,四个角各切掉一个边长为5厘米的正方形后,做成一个无盖的长方体盒子。做这个盒子用了多少平方厘米铁皮?它的容积是多少立方分米?
45.“火树银花元夕夜,彩灯万盏熠霞流。”为弘扬中华优秀传统文化,元宵节前夕,学校手工社团的同学们做了24盏纱灯和32盏礼花灯,准备参加灯展。把这些灯笼分装到纸箱里,不能混装且每箱的灯笼数量要相等,每箱最多能装几盏灯笼?
46.研学一班有队员48人,研学二班有队员42人。如果把两个班的学生分别分成若干小组,要使两个班每个小组的人数相同,每个小组最多有几人?
47.一辆公交车在始发站上车28人,在文化广场下去a人,又上来b人。
(1)用式子表示现在车上的人数。
(2)当a=9,b=12时,现在车上有多少人?
48.在一根木棍上,有三种刻度线,第一种刻度线将木棍分成10等份;第二种刻度线将木棍分成 12等份:第三种刻度线将木棍分成15等份。如果沿每条刻度线将木锯断,木棍总共被锯成多少段?
49.一个旅游团租车出游,平均每人应付车费40元.后来又增加了8个人,这样每人应付的车费是35元,租车费是多少元?
50.从神舟七号到神舟十八号载人飞船的成功发射,展示了中国载人航天工程在过去十六年中的巨大变化。学校组织五年级8名老师和155名同学前往某航天馆参观,每辆车限载乘客40 人(不算司机),准备出发时发现还剩余3人没有座位。
收费标准 个人票:50元/人(学生半价)
团体票:100人以上(含100人)26元/人
(1)学校一共租了几辆车 (列方程解答)
(2)航天馆的售票方式如图。全员怎样购票更划算
参考答案及试题解析
1.56
【解析】解:12×2+6×2+5×4
=24+12+20
=56(dm)
故答案为:56。
【分析】看图及根据题意可知防撞条由长方体茶几的2条长、2条宽和4条高组成,因此,长×2+宽×2+高×4=至少需要的防撞条长度。
2.80-5a;55
【解析】饭店里运来80袋大米,每天吃a袋,5天后还剩(80-5a)袋。当a=5时,还剩:80-5×5=55(袋)。
故答案为:80-5a;55。
【分析】用每天吃的袋数乘吃的天数求出5天吃的袋数,用总数减去5天吃的袋数表示出还剩的袋数。把a的值带换成5,求出还剩的袋数即可。
3.0或6
【解析】解:设三位数为75M,
则M必须取偶数0,2,4,6,8,
又因为7+5+M=12+M能被3整除,则M只能取0或6。
故答案为:0或6
【分析】一个数能被2整除的条件是其个位数为偶数(即0、2、4、6、8)。
一个数能被3整除的条件是其各个数位上的数字之和能被3整除。
对于三位数75 :
考虑被2整除的条件,这意味着 必须为偶数(0、2、4、6、8)。
考虑被3整除的条件,计算75 的数字之和,即7+5+ 必须能被3整除。
计算数字之和并寻找符合条件的 值:当 =0时,数字之和为7+5+0=12,能被3整除。
当 =2时,数字之和为7+5+2=14,不能被3整除。
当 =4时,数字之和为7+5+4=16,不能被3整除。
当 =6时,数字之和为7+5+6=18,能被3整除。
当 =8时,数字之和为7+5+8=20,不能被3整除。
因此,只有当 =0或 =6时,三位数75 同时满足能被2和3整除的条件。
4.22
【解析】解:在1~9这九个数中,质数有2、3、5、7。其中,只有2和3是相邻的。所以,a=2,b=3。
在1~9这九个数中,合数有4、6、8、9。其中,只有8和9是相邻的。所以,m=8,n=9。
所以,a+b+m+n=2+3+8+9=22。
故答案为:22
【分析】首先,我们需要确定在1~9这九个数中,哪些是质数,哪些是合数。质数是只有1和它本身两个正因数的自然数,而合数则是有其他正因数的自然数。然后,根据题目条件,我们需要找出相邻的质数和相邻的合数。最后,将这些数相加,得到最终的答案。
5.192;64
【解析】解:4×4×4×3
=64×3
=192(cm3)
4×4×4
=16×4
=64(cm2)
故答案为:192;64。
【分析】通过实际操作可知用3个棱长是4cm的小正方体拼成一个长方体,则长方体表面积与原3个正方体表面积的和比较会减少4个接触面的面积和,而长方体的体积等于3个小正方体体积的和,因此,棱长×棱长×棱长=一个小正方体的体积,棱长×棱长×棱长×3=长方体的体积,棱长×棱长=一个接触面的面积,棱长×棱长×4=减少的表面积。
6.;等腰
【解析】解:1--
=-
=(m),
它是一个等腰三角形;
故答案为:;等腰。
【分析】根据题意,已知三角形周长及两条边长,首先计算第三条边的长度,再根据边长关系判断三角形类型。
7.12;18;8;0.75
8.b;a
【解析】解:如果a÷b=5(a、b都是不等于0的自然数),那么a、b的最大公因数是b,最小公倍数是a。
故答案为:b;a。
【分析】一个数是另一个数的倍数,那么较小数就是他们的最大公因数,较大数就是他们的最小公倍数。
9.<;<;>;>
10.3
【解析】解:设小灰兔用x个大白菜换小白兔y根胡萝卜。
120-x+y=(120+180)÷2
120-x+y=150
y-x=30
又因为10
所以x=15,y=45
y÷x=3
一个大白菜可以换3根胡萝卜。
故答案为:3
【分析】 首先未知数,即1棵白菜可以换多少只胡萝卜。然后,根据题目给出的条件建立一个等式来表示小白兔和小灰兔的粮食数量相等的情况。接下来通过解这个方程来找到未知数的值,即一棵大白菜可以换多少只胡萝卜。
11.乙
【解析】假如工作年限为n年。在甲公司拿的年薪为:18000+2000+2000×1+2000×2+2000×3+···+2000×n
=18000+1000(1+n)n
=18000+500((2+2n)n
在乙公司拿的年薪为:9000+9000+500×1+500×2+500×3+500×4+···+500×2n
=18000+500(1+2n)n
18000+500((2+2n)n>18000+500(1+2n)n
所以在甲公司拿的年薪高。
【分析】把甲的年薪表示出来,把乙方年薪表示出来,然后再比较。
12.22
【解析】解:根据题意,可得
xy=2x+4y+7
xy-2x-4y-7=0
xy-2x-4y+8-8-7=0
(x-4)(y-2)=15
因为15=1×15=3×5
所以,x-4=1,y-2=15或x-4=3,y-2=5
解得,x=5,y=17或x=7,y=7
因为x,y是不同的素数,所以,x=7,y=7不符合,舍去
所以,x=5,y=17
所以,x+y=5+17=22
故答案为:22
【分析】将原等式移项并用十字相乘法进行因式分解,得到(x-4)(y-2)=15。由于x和y是不同的素数,则x-4和y-2也是整数,且只能是1和15或3和5。 解得x=5,y=17,据此即可求解
13.2700
【解析】解:设这批杯子共有x个,则平均每箱有个。
60+x=15×
60+x=
3600+32x=35x-4500
3x=8100
x=8100÷3
x=2700
故答案为:2700。
【分析】依据等量关系式:余下的个数+剩下的分率×杯子的总个数=剩下可以装满的箱数×平均每箱杯子的个数。
14.正确
【解析】
x÷8=7.2
解:x=7.2×8
x=57.6
当x=57.6时,代入方程 6a-x=51.6 ,
即6a-57.6=51.6
解:6a=51.6+57.6
6a=109.2
a=109.2÷6
a=18.2
故答案为:正确。
【分析】根据被除数=商×除数,求出方程x÷8=7.2的解,然后把x的解代入6a-x=51.6,变成6a-57.6=51.6,再根据被减数=差+减数,一个因数=积÷另一个因数即可。
15.错误
【解析】解:因为a>c,当a<0时,则c<0,t<0时,则 ×t<1;
当a<0时,则c<0,t>0时,则 ×t>1;
当c>0时,则a>0,t≤0时,则 ×t<1;
当c>0时,则c>0,t>0时,则 ×t>1;
当a<0时,则c<0,t<0时,则 ×t<1;
故答案为:错误.
【分析】因为a>c,然后考虑a和c的取值及t的取值,进而得出解论.解答此题的关键是,要考虑a和c的取值及t的取值,做出相应的判断.
16.正确
17.错误
【解析】 一个正方体的棱长扩大为原来的3倍,它的体积就扩大为原来的27倍,原题说法错误。
故答案为:错误。
【分析】 根据正方体的体积公式:V=a3,正方体的棱长扩大到原来的3倍,它的体积扩大3×3×3=27倍,据此判断。
18.错误
【解析】解:这是等式,又含有未知数,是方程,原题说法错误.
故答案为:错误
【分析】含有未知数的等式叫做方程,由此根据方程的意义判断即可.
19.错误
【解析】 表面积和体积不能比较大小,原题说法错误。
故答案为:错误。
【分析】 立体图形的表面积是指组成它的所有面的面积和,而其体积是指它所占空间的大小,所以二者意义不一样,不能比较大小,据此判断。
20.正确
【解析】解:两个质数相乘,得到的积一定是合数,原题说法正确。
故答案为:正确。
【分析】两个质数相乘,得到的积最少有3个因数,所以一定是合数。
21.错误
【解析】解:假分数的倒数小于或等于1,原题说法错误。
故答案为:错误。
【分析】假分数大于或等于1,所以假分数的倒数小于或等于1。
22.错误
【解析】等式左边加一个数,右边减去同一个数,这个数只有是0时,所得结果仍然是等式,其他数都不是等式.
故答案为错误.
【分析】这道题主要考查了等式的基本性质.等式的基本性质:等式的两边同时加上或减去同一个数,同时乘或除以一个非零数,等式仍然成立.
23.正确
【解析】解:a的最大因数是它本身,b的最小倍数是它本身,那么a与b相等。
故答案为:正确。
【分析】一个数的最大因数与最小倍数都等于它本身,所以a与b相等。
24.D
【解析】解:<□< , 在□里填分数, 有无数种填法。
故答案为:D。
【分析】任意两个分数之间有无数个分数,据此解答。
25.B;D
【解析】解:质数×质数=合数;奇数+奇数=偶数。
故答案为:B;D。
【分析】质数是一个大于1的自然数,除了1和它本身以外,不能被其他自然数整除的数;合数是一个大于1的自然数,除了1和它本身以外,还能被其他自然数整除的数;所以当两个质数相乘时,它们的积一定能被这两个质数相乘,它们的积一定是合数。能够被2整除叫做偶数,不能被2整除叫做奇数;两个奇数相加一定能被2整除,所以它们的和一定是偶数。
26.C
【解析】解:4×a+3×b=(4a+3b)(根)。
故答案为:B。
【分析】共需要用小棒的根数=摆一个正方形需要小棒的根数×摆正方形的个数+摆一个三角形需要小棒的根数×摆三角形的个数。
27.C
【解析】解:把一个长方体分成几个小正方体后,这些小正方体的表面积之和比原来大了。
故答案为:C。
【分析】把一个长方体分成几个小正方体后,表面积比原来多了切面的面积,所以这些小正方体的表面积之和比原来大了。
28.C
【解析】解:减少了:a×a×2=2a .
故答案为:C
【分析】把两个正方体拼在一起后会减少两个正方形的面,每个正方形的面积是a×a,由此计算即可.
29.B
【解析】解:A:不是所有的质数都是奇数,原来说法错误;
B:除了 2 以外,任意两个质数的和一定是偶数,原来说法正确;
C:奇数-奇数=偶数,原来说法错误;
D:不是任意两个自然数的积都是合数。原来说法错误。
故答案为:B。
【分析】A:质数是只有1和本身两个因数的数,最小的质数2是偶数,也是所有质数中唯一的偶数;
B:质数中除了2之外都是奇数,两个奇数的和一定是偶数;
C:奇数-奇数=偶数,奇数+奇数=偶数;
D:例如自然数1和3的积就是质数,由此判断即可。
30.C
【解析】解:一种水箱最多可以装4升水,我们就说这种水箱的是容积4升。
故答案为:C。
【分析】容器所能容纳物体的体积就是它的容积。
31.C
【解析】解:下面事件适合用下图来表示的是①④。
故答案为:C。
【分析】①某冷饮店冰激棱各月的销量可以用单式折线统计图表示;
②某同学一到六年级的身高变化,折线趋势不会下降的;
③6种不同品牌汽车销售的销量,要用条形统计图;
④某位小学生考试成绩的变化可以用单式折线统计图表示。
32.A
【解析】解:与比较,分数大小相同,分数的意义不同。
的分数单位是,的分数单位是,因为>,所以的分数单位较大。
故答案为:A。
【分析】与比较大小,先将单位统一,再比较分子的大小。
分数的意义:把单位1平均分成若干份,表示这样一份或几份的数,叫做分数。本题中是将单位1平均分成3份,取其中的2份;是将单位1平均分成9份,取其中的6份。
把单位“1”平均分成若干份取其中的一份的数,叫做分数单位。即分子是1,分母是正整数的分数,又叫单位分数,记为。
33.B
【解析】8=2×2×2,
10=2×5,
8和10的最小公倍数是2×2×2×5=40,
第二次同时发车的时间是6时+40分=6时40分。
故答案为:B。
【分析】此题主要考查了最小公倍数的应用,先将8和10分别分解质因数,然后求出8和10的最小公倍数,最后用首班车发车时间+最小公倍数=第二次同时发车的时刻,据此列式解答。
34.D
【解析】解:A:三角和黑色面不相邻,此选项错误;
B:三角应该在左边。此选项错误;
C:三角和黑色面不相邻,此选项错误;
D:正确。
故答案为:D。
【分析】观察三个面的位置,这三个面是相邻的,根据正方体的特征确定展开图即可。
35.C
【解析】200÷5 =40(厘米)
40÷4=10(厘米) 10-5=5(厘米)
10×10×5=500(立方厘米)
故答案为:C
【分析】
读题可知长方体底面为正方形,通过增加的表面积求出底面周长,(增加表面积为底面周长×增加的高),进而得出底面边长和原长方体的高,最终由体积公式:长×宽×高计算出体积。
36. = = = 1-0.89=0.11 =5
= = 0.95- =0.15 =1 =
【解析】
【分析】同分母分数相加减,分母不变,分子相加减;异分母分数相加减,先通分,然后按照同分母分数加减法的法则进行计算。
37.解:(1)
=
=
(2)
=
=+
=
(3)
=
=
=
(4)
=
=
=1-
=
(5)
=
=
=
(6)
=
=
=
【解析】(1)先将各个减数化成相同分母的分数形式,再根据分数的减法运算规则进行计算。
(2)先将分数转换为小数,再进行加法运算。
(3)先按照运算法则先计算括号内的运算,然后执行括号外的运算。
(4)首先识别表达式中的运算,然后根据分数的性质进行简化,最后完成计算。
(5)先找到一个公共分母,将各分数转换为同分母形式,之后进行加减运算即可得到结果。
(6)本题主要考查异分母分数的加减运算,需要先将异分母分数通过通分变为同分母分数,然后进行加减运算。
38.x=0.396;x=0.3;x=0.7
39.解:(10×4+10×6+6×4)×2
=(40+60+24)×2
=124×2
=248(cm2)
4×6×10
=24×10
=240(cm3)
5×5×6
=25×6
=150(dm2)
5×5×5
=25×5
=125(dm3)
(4×4+4×6+4×6)×2
=(16+24+24)×2
=64×2
=128(cm2)
4×4×6
=16×6
=96(cm3)
【解析】长方体的表面积=(长×宽+长×高+宽×高)×2;长方体的体积 =长×宽×高;正方体表面积=棱长×棱长×6;正方体体积=棱长×棱长×棱长,据此列式解答。
40.(1);
(2)
【解析】解:(1)图形⑥的面积是2×2=4(cm2), 图形①的面积是4×4÷2=8(cm2), 4÷8=;
图形⑦的面积是4×2÷2=4(cm2), 整个图案的总面积是4×4÷2×2+2×2÷2×2+2×2×2+4×2÷2=32(cm2)
4÷32=
故答案为:(1);。
【分析】(1)平行四边形的面积=底×高,三角形的面积=底×高÷2,正方形的面积=边长×边长,分别求出各图形的面积,要求一个数是另一个数的几分之几,用除法计算;
(2)平移作图的步骤:①找出能表示图形的关键点;②确定平移的方向和距离;③按平移的方向和距离确定关键点平移后的对应点;④按原图的顺序,连接各对应点,据此作图即可;
画轴对称图形的步骤:①点出关键点,找出所有的关键点,即图形中所有线段的端点;②确定关键点到对称轴的距离,关键点离对称轴多远,对称点就离对称轴多远;③点出对称点;④连线,按照给出的一半图形将所有对称点连接成线段。
41.解:1--
=-
=
答:进行跳舞的同学占全班人数的。
【解析】单位1-唱歌的同学占全班人数的几分之几-诗歌朗诵的同学占全班人数的几分之几=跳舞的同学占全班人数的几分之几。
42.解:设2022年哈尔滨冰雪大世界接待游客x万人次。
5x+21=271
5x=271-21
5x=250
x=250÷5
x=50
答:2022年哈尔滨冰雪大世界接待游客50万人次。
【解析】设2022年哈尔滨冰雪大世界接待游客x万人次。 依据等量关系式:2022年哈尔滨冰雪大世界接待游客的人数×5+多的人数=2023年哈尔滨冰雪大世界接待游客的人数,列方程,解方程。
43.(1)21平方分米
(2)1分米
44.500平方厘米;1立方分米
45.解:24和32的最大公因数是8
答:每箱最多能装8盏灯笼。
【解析】因为装箱时,不能混装且每箱的灯笼数量要相等,那么每箱最多能装灯笼的盏数就是24和32的最大公因数,据此作答即可。
46.解:
48和42的最大公因数是:2×3=6
答:每个小组最多有6人。
【解析】每个小组最多的人数=48和42的最大公因数,用短除法求出。
47.(1)解:用式子表示现在车上的人数(28﹣a+b)人。
(2)解:当a=9,b=12时,
28﹣a+b=28﹣9+12=31
答:现在车上有31人。
【解析】(1)现在车上的人数=一辆公交车在始发站上车的人数-在文化广场下去的人数+又上来的人数;
(2)把a=9,b=12代入计算。
48.设木棍的长度为60厘米。
计算每种刻度线的数量:
10等分的每等分长6cm
刻度线数量,10-1=9(条),
12等分的每等分长5cm为
刻度线数量,12-1=11(条),
15等分的为每等分长4cm
刻度线数量,15-1=14(条)。
计算重合的刻度线数量:
第一种与第二种刻度线重合的条数:
6和5的公倍数是30,有1条。
第一种与第三种刻度线重合的条数:
6和4的公倍数是12、24、36、有4条
第二种与第三种刻度线重合的条数:
5和4的公倍数是20,40,有2条。
计算总的刻度线数量:
因此,共有刻度线9+11+14-1-4-2=27(条)。
计算木棍被锯成的段数:
木棍总共被锯成27+1=28(段)
答: 木棍总共被锯成28段。
【解析】首先,设木棍的长度为60厘米(这是10、12和15的最小公倍数,以便于计算)。然后,计算每种刻度线的数量。接着,找出哪些刻度线是重合的,并计算重合的刻度线数量。最后,计算总的刻度线数量,并据此得出木棍被锯成的段数。
49.解:设原来的乘车人数是x人, 40x=35(x+8) 40x=35x+28040x﹣35x=35x+280﹣35x 5x=280 x=5640×56=2240(元)答:租车费是2240元。
【解析】根据人数增加前后的车费不变找等量关系,等量关系:原来人数×每人应付的钱数=增加后的人数×增加后每人应付的钱数,根据等量关系列方程,解方程。
50.(1)解:设一共租了x辆车。
40x+3=8+155
40x+3=163
40x+3-3=163-3
40x=160
40x÷40=160÷40
x=4
答:学校一共租了4辆车。
(2)解:全员购买个人票
50÷2=25(元),
8×50+155×25=4275(元),
全员购买团体票:
(8+155)×26=4238(元),
8名老师和92名学生购买团体票,剩余63名学生购买个人票:100×26+63×25=4175(元),因为4175<4238<4275,
所以8名老师和92名学生购买团体票,剩下63 名学生买个人票更划算,
答:8名老师和92 名学生购买团体票,剩下63名学生买个人票更划算。
【解析】(1) 还剩余3人没有座位 ,说明师生总数比座位数多3,即座位数+3=师生总数。设一共租了x辆车,座位数40X,师生总数155+8.据此列出方程求解。
(2)分三种情况讨论:1、全员购买个人票;2、全员购买团体票;8名教师和92名学生买团体票,剩下学生买个人票(半价)。分别计算出三种购票方式所需要的钱数,然后作比较那种方式划算。
21世纪教育网(www.21cnjy.com)
同课章节目录
