1.1.1探索勾股定理 课件(共18张PPT) 北师大版(2024)数学八年级上册
文档属性
| 名称 | 1.1.1探索勾股定理 课件(共18张PPT) 北师大版(2024)数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 725.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
北师大版八年级数学上册
第一章 勾股定理
1.1.1 探索勾股定理
情景引入
由于安全问题,电力工人打算加一条钢索用来稳固电线杆.从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么电力工人应准备多长的钢索?
学习目标
1.经历勾股定理探索的过程,理解并掌握直角三角形三边之间的数量关系
2.能够运用勾股定理进行简单的计算
合作交流,探索新知
(1)在方格纸上画若干个直角三角形,分别测量它们的三条边,看看三条边的平方之间有怎样的关系?
(思考·交流)
合作交流,探索新知
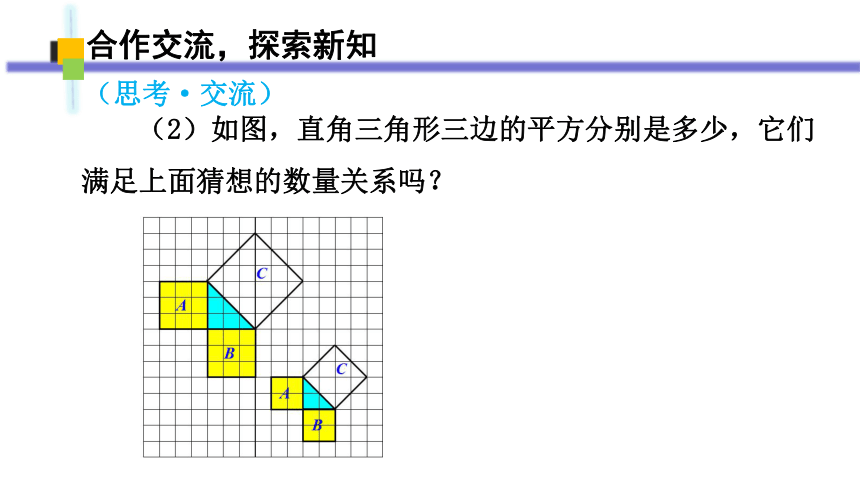
(2)如图,直角三角形三边的平方分别是多少,它们满足上面猜想的数量关系吗?
(思考·交流)
合作交流,探索新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
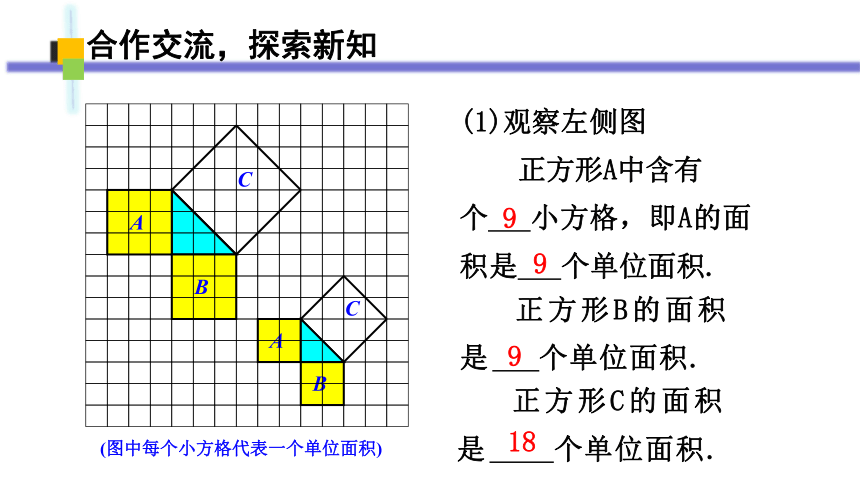
(1)观察左侧图
正方形A中含有 个 小方格,即A的面积是 个单位面积.
正方形B的面积是 个单位面积.
正方形C的面积是 个单位面积.
9
9
9
18
合作交流,探索新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
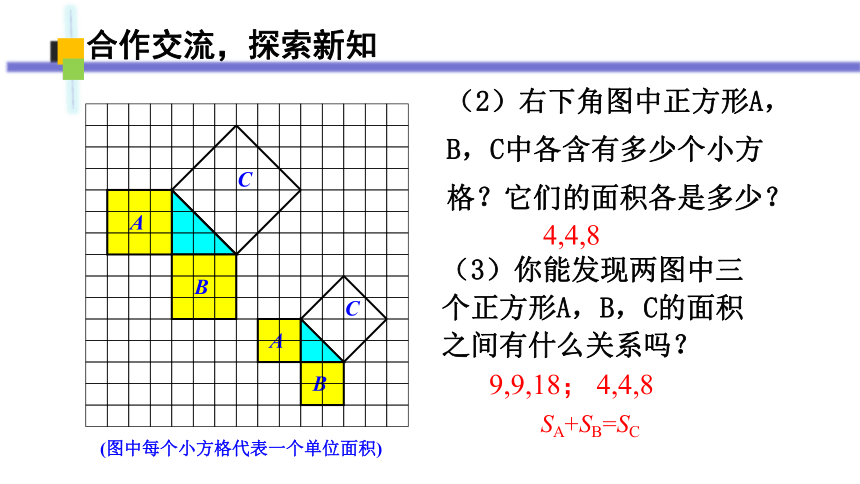
(2)右下角图中正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
4,4,8
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
9,9,18; 4,4,8
SA+SB=SC
合作交流,探索新知
(3)如果直角三角形的两直角边长分别为1.6个单位长度和2.4个单位长度,那么上面所猜想的数量关系还成立吗?说说你的理由
(思考·交流)
归纳总结
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在Rt△ABC中 ,
∵∠C=90°,
∴由勾股定理得a2+b2=c2.
数学语言:
如果a,b和c分别表示直角三角形的两直角边和斜边,
那么a2+b2=c2.
课外阅读——数学小知识
我国古代称直角三角形的较短的直角边为勾,较长的直角边为股,斜边为弦,这便是勾股定理的由来。
精讲精练,应用新知
例1:如图直角三角形两直角边长分别为BC=3cm,AC=4cm,求斜边AB的长度.
D
思考:如何求AB边上的高呢?
解:由题知在Rt△ABC中 ,
∵∠ACB=90°,
∴由勾股定理得AC2+BC2=AB2.
即:32+42=AB2
∵AB>0
∴AB=5cm
等面积法求高
精讲精练,应用新知
精练1:求下列图形中未知边的长度
解:由题知在Rt△ABC中∵∠ACB=90°,
∴由勾股定理得AC2+BC2=AB2.
即:62+x2=102
∴BC2=102-62=64
∵BC>0∴BC=8
例2:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,四边形ADEB为长方形,且AD=2,则S长方形ADEB= .
精讲精练,应用新知
精练2:如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 .
精讲精练,应用新知
1.(教材P3随堂练习1)求下图中字母所代表的正方形的面积。
(1)
(2)
解:A 所代表的正方形的面积是625;
B 所代表的正方形的面积是144.
当堂检测,巩固新知
2.(教材P3随堂练习2)小明家买了一台55in(1 in=25.4mm)的电视机。小明量了电视机的屏幕后,发现屏幕只有121.5cm长和68.5cm宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
当堂检测,巩固新知
解:不同意,理由如下:
电视机的尺寸是指屏幕的对角线长
课堂总结,升华新知
本节课你都有哪些收获?
课堂总结,升华新知
认识勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
北师大版八年级数学上册
第一章 勾股定理
1.1.1 探索勾股定理
情景引入
由于安全问题,电力工人打算加一条钢索用来稳固电线杆.从电线杆离地面8m处向地面拉一条钢索,如果这条钢索在地面的固定点距离电线杆底部6m,那么电力工人应准备多长的钢索?
学习目标
1.经历勾股定理探索的过程,理解并掌握直角三角形三边之间的数量关系
2.能够运用勾股定理进行简单的计算
合作交流,探索新知
(1)在方格纸上画若干个直角三角形,分别测量它们的三条边,看看三条边的平方之间有怎样的关系?
(思考·交流)
合作交流,探索新知
(2)如图,直角三角形三边的平方分别是多少,它们满足上面猜想的数量关系吗?
(思考·交流)
合作交流,探索新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
(1)观察左侧图
正方形A中含有 个 小方格,即A的面积是 个单位面积.
正方形B的面积是 个单位面积.
正方形C的面积是 个单位面积.
9
9
9
18
合作交流,探索新知
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
(2)右下角图中正方形A,B,C中各含有多少个小方格?它们的面积各是多少?
4,4,8
(3)你能发现两图中三个正方形A,B,C的面积之间有什么关系吗?
9,9,18; 4,4,8
SA+SB=SC
合作交流,探索新知
(3)如果直角三角形的两直角边长分别为1.6个单位长度和2.4个单位长度,那么上面所猜想的数量关系还成立吗?说说你的理由
(思考·交流)
归纳总结
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
在Rt△ABC中 ,
∵∠C=90°,
∴由勾股定理得a2+b2=c2.
数学语言:
如果a,b和c分别表示直角三角形的两直角边和斜边,
那么a2+b2=c2.
课外阅读——数学小知识
我国古代称直角三角形的较短的直角边为勾,较长的直角边为股,斜边为弦,这便是勾股定理的由来。
精讲精练,应用新知
例1:如图直角三角形两直角边长分别为BC=3cm,AC=4cm,求斜边AB的长度.
D
思考:如何求AB边上的高呢?
解:由题知在Rt△ABC中 ,
∵∠ACB=90°,
∴由勾股定理得AC2+BC2=AB2.
即:32+42=AB2
∵AB>0
∴AB=5cm
等面积法求高
精讲精练,应用新知
精练1:求下列图形中未知边的长度
解:由题知在Rt△ABC中∵∠ACB=90°,
∴由勾股定理得AC2+BC2=AB2.
即:62+x2=102
∴BC2=102-62=64
∵BC>0∴BC=8
例2:如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,四边形ADEB为长方形,且AD=2,则S长方形ADEB= .
精讲精练,应用新知
精练2:如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为 .
精讲精练,应用新知
1.(教材P3随堂练习1)求下图中字母所代表的正方形的面积。
(1)
(2)
解:A 所代表的正方形的面积是625;
B 所代表的正方形的面积是144.
当堂检测,巩固新知
2.(教材P3随堂练习2)小明家买了一台55in(1 in=25.4mm)的电视机。小明量了电视机的屏幕后,发现屏幕只有121.5cm长和68.5cm宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?
当堂检测,巩固新知
解:不同意,理由如下:
电视机的尺寸是指屏幕的对角线长
课堂总结,升华新知
本节课你都有哪些收获?
课堂总结,升华新知
认识勾股定理
如果直角三角形两直角边长分别为a,b,斜边长为 c ,那么a2+b2=c2
利用勾股定理进行计算
同课章节目录
