2.2 第1课时 有理数的加法法则 课件(共23张PPT) 北师大版数学七年级上册
文档属性
| 名称 | 2.2 第1课时 有理数的加法法则 课件(共23张PPT) 北师大版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
北师大版数学七年级上册
第二章 有理数及其运算
汇报人:孙老师
汇报班级:X级X班
2.2 有理数的加减运算
2.2 第1课时 有理数的加法法则
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.经历探索有理数加法法则的过程,体会分类和归纳的思想方法;
2.理解有理数的加法法则;
3.能熟练地进行有理数加法的运算.
第贰章节
新课导入
新课导入
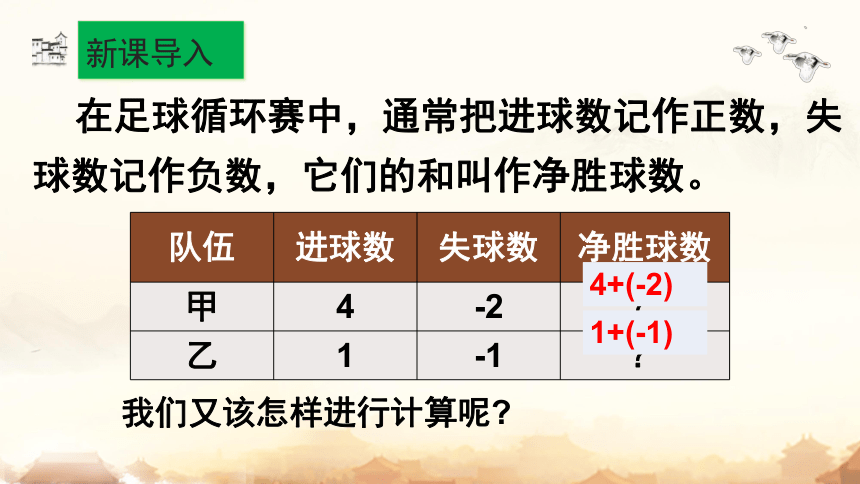
在足球循环赛中,通常把进球数记作正数,失球数记作负数,它们的和叫作净胜球数。
队伍 进球数 失球数 净胜球数
甲 4 -2 ?
乙 1 -1 ?
4+(-2)
1+(-1)
我们又该怎样进行计算呢
第叁章节
新知探究
新知探究
活动:某班举行知识竞赛,评分标准是:
答对 1 题加 1 分,答错 1 题扣 1 分,不回答得 0 分。 每个参赛队的基本分均为 0 分。
“加 1 分、扣 1 分,得 0 分”、“扣 1 分、加 1 分,得 0 分”可以如何表示?
(+1) + (-1) = 0
(-1) + (+1) = 0
有理数的加法
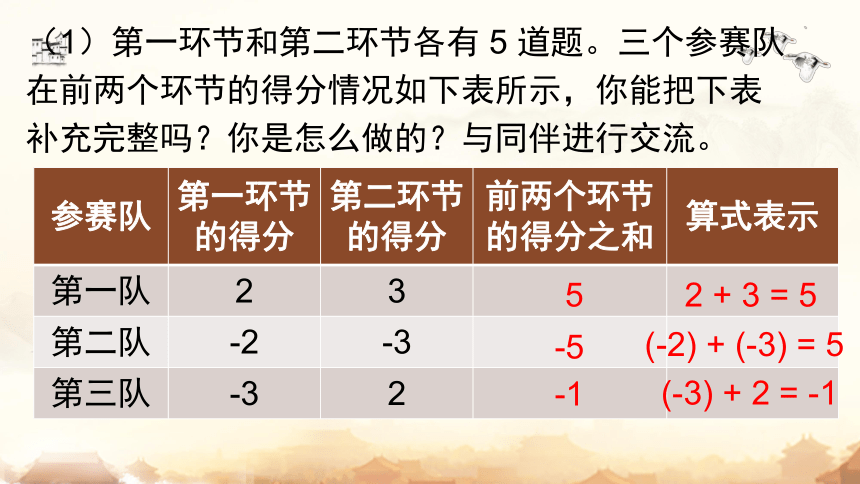
(1)第一环节和第二环节各有 5 道题。三个参赛队在前两个环节的得分情况如下表所示,你能把下表补充完整吗?你是怎么做的?与同伴进行交流。
参赛队 第一环节的得分 第二环节的得分 前两个环节的得分之和 算式表示
第一队 2 3
第二队 -2 -3
第三队 -3 2
5
-5
-1
2 + 3 = 5
(-2) + (-3) = 5
(-3) + 2 = -1
(2)小明用 1 个 表示 +1,用 1个 表示 -1,用 直观表示 (+1) + (-1) = 0,用 直观表示
(-1) + (+1) = 0。他列出了两个算式,并给出了直观的解释,你能理解他的做法吗?
→
→
(-2) + (-3) = -5
(-3) + 2 = -1
解:可能会出现:5 + (-5) = 0 或 -5 + 0 = -5
(3)如果有第四个参赛队,那么第四队前两个环节的得分可能会出现哪些情形,据此可以列出哪些算式?你能直观解释运算过程和结果吗?
→
→
( - 2 ) + ( - 3 ) = - ( 2 + 3 )= - 5
两个有理数相加,和的符号怎样确定?和的绝对值如何确定?
两个加数的绝对值相加
同号两数相加
取相同符号
议一议
↓ ↓ ↓
( + 2 ) + ( + 3 ) = + ( 2 + 3 )= + 5
( - 5 ) + ( + 5 ) = - ( 5 - 5) = 0
↓ ↓
异号两数相加,绝对值相等
↓
和为 0
( - 3 ) + (+ 2) = - ( 3 - 2) = - 1
↓ ↓ ↓
较大的绝对值减去较小的绝对值
异号两数相加,
绝对值不等
取绝对值较大的数的符号
( - 5 ) + 0 = - ( 5 - 0) = - 5
与 0 相加
仍得这个数
有理数加法法则:
归纳总结
异号两数相加,绝对值相等时和为 0;
同号两数相加,取相同的符号,并把绝对值相加;
绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减较小的绝对值。
一个数同 0 相加,仍得这个数。
例1 计算:
(1) 180 + (-10); (2) (-10) + (-1);
(3) 5 + (-5); (4) 0 + (-2)。
解:(1)180 + (-10) = +(180 - 10) = 170;
典例精析
(2)(-10) + (-1) = -(10 + 1) = -11;
(3)5 + (-5) = 0;
(4)0 + (-2) = -2。
第肆章节
随堂练习
随堂练习
1.计算:(-2)+(-5)= ( )
A. -7
B. 7
C. -3
D.3
2.如图,数轴上A,B两点表示的数的和是( )
A. 1
B. -2
C. -3
D.2
A
B
3.下列各式中,计算结果为正的是( )
A. (-3) + 5
B. (-6) + 2
C. 4.1+(-5.5)
D. 0+(-)
4.已知|a|=1,b是2的相反数,则a+b的值为_______。
A
-3或-1
5.计算:
(1) (-18)+35;
(2) (-8)+0;
(3) (-15)+(-19);
(4) (-4 )+ 4 。
解:原式=17;
解:原式=-8;
解:原式=-34;
解:原式= 0。
解:用正号表示上升,用负号表示下降。
6.某直升机在空中做升降练习,第一次上升210 m,第二次下降232 m,请问此时直升机是否又回到了原来的高度?如果没有,比原来升高了还是降低了?升高或降低了多少?
(+210)+(-232)=-22(m)。
因此,此时直升机没有回到原来的高度,比原来降低了,降低了22 m。
第伍章节
课堂小结
课堂小结
有理数的加法
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加
2.异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值
3.一个数同0相加,仍得这个数
有理数加法法则的运用:
1.首先判断加法类型;
2.再确定和的符号;
3.最后确定和的绝对值
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
北师大版数学七年级上册
第二章 有理数及其运算
汇报人:孙老师
汇报班级:X级X班
2.2 有理数的加减运算
2.2 第1课时 有理数的加法法则
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.经历探索有理数加法法则的过程,体会分类和归纳的思想方法;
2.理解有理数的加法法则;
3.能熟练地进行有理数加法的运算.
第贰章节
新课导入
新课导入
在足球循环赛中,通常把进球数记作正数,失球数记作负数,它们的和叫作净胜球数。
队伍 进球数 失球数 净胜球数
甲 4 -2 ?
乙 1 -1 ?
4+(-2)
1+(-1)
我们又该怎样进行计算呢
第叁章节
新知探究
新知探究
活动:某班举行知识竞赛,评分标准是:
答对 1 题加 1 分,答错 1 题扣 1 分,不回答得 0 分。 每个参赛队的基本分均为 0 分。
“加 1 分、扣 1 分,得 0 分”、“扣 1 分、加 1 分,得 0 分”可以如何表示?
(+1) + (-1) = 0
(-1) + (+1) = 0
有理数的加法
(1)第一环节和第二环节各有 5 道题。三个参赛队在前两个环节的得分情况如下表所示,你能把下表补充完整吗?你是怎么做的?与同伴进行交流。
参赛队 第一环节的得分 第二环节的得分 前两个环节的得分之和 算式表示
第一队 2 3
第二队 -2 -3
第三队 -3 2
5
-5
-1
2 + 3 = 5
(-2) + (-3) = 5
(-3) + 2 = -1
(2)小明用 1 个 表示 +1,用 1个 表示 -1,用 直观表示 (+1) + (-1) = 0,用 直观表示
(-1) + (+1) = 0。他列出了两个算式,并给出了直观的解释,你能理解他的做法吗?
→
→
(-2) + (-3) = -5
(-3) + 2 = -1
解:可能会出现:5 + (-5) = 0 或 -5 + 0 = -5
(3)如果有第四个参赛队,那么第四队前两个环节的得分可能会出现哪些情形,据此可以列出哪些算式?你能直观解释运算过程和结果吗?
→
→
( - 2 ) + ( - 3 ) = - ( 2 + 3 )= - 5
两个有理数相加,和的符号怎样确定?和的绝对值如何确定?
两个加数的绝对值相加
同号两数相加
取相同符号
议一议
↓ ↓ ↓
( + 2 ) + ( + 3 ) = + ( 2 + 3 )= + 5
( - 5 ) + ( + 5 ) = - ( 5 - 5) = 0
↓ ↓
异号两数相加,绝对值相等
↓
和为 0
( - 3 ) + (+ 2) = - ( 3 - 2) = - 1
↓ ↓ ↓
较大的绝对值减去较小的绝对值
异号两数相加,
绝对值不等
取绝对值较大的数的符号
( - 5 ) + 0 = - ( 5 - 0) = - 5
与 0 相加
仍得这个数
有理数加法法则:
归纳总结
异号两数相加,绝对值相等时和为 0;
同号两数相加,取相同的符号,并把绝对值相加;
绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减较小的绝对值。
一个数同 0 相加,仍得这个数。
例1 计算:
(1) 180 + (-10); (2) (-10) + (-1);
(3) 5 + (-5); (4) 0 + (-2)。
解:(1)180 + (-10) = +(180 - 10) = 170;
典例精析
(2)(-10) + (-1) = -(10 + 1) = -11;
(3)5 + (-5) = 0;
(4)0 + (-2) = -2。
第肆章节
随堂练习
随堂练习
1.计算:(-2)+(-5)= ( )
A. -7
B. 7
C. -3
D.3
2.如图,数轴上A,B两点表示的数的和是( )
A. 1
B. -2
C. -3
D.2
A
B
3.下列各式中,计算结果为正的是( )
A. (-3) + 5
B. (-6) + 2
C. 4.1+(-5.5)
D. 0+(-)
4.已知|a|=1,b是2的相反数,则a+b的值为_______。
A
-3或-1
5.计算:
(1) (-18)+35;
(2) (-8)+0;
(3) (-15)+(-19);
(4) (-4 )+ 4 。
解:原式=17;
解:原式=-8;
解:原式=-34;
解:原式= 0。
解:用正号表示上升,用负号表示下降。
6.某直升机在空中做升降练习,第一次上升210 m,第二次下降232 m,请问此时直升机是否又回到了原来的高度?如果没有,比原来升高了还是降低了?升高或降低了多少?
(+210)+(-232)=-22(m)。
因此,此时直升机没有回到原来的高度,比原来降低了,降低了22 m。
第伍章节
课堂小结
课堂小结
有理数的加法
有理数加法法则:
1.同号两数相加,取相同的符号,并把绝对值相加
2.异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值
3.一个数同0相加,仍得这个数
有理数加法法则的运用:
1.首先判断加法类型;
2.再确定和的符号;
3.最后确定和的绝对值
北师大版数学七年级上册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
同课章节目录
