六年级数学下册课件 用“转化”的策略解决图形问题(苏教版)
文档属性
| 名称 | 六年级数学下册课件 用“转化”的策略解决图形问题(苏教版) |
|
|
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-02 00:00:00 | ||
图片预览







文档简介
课件44张PPT。用“转化”的策略解决图形问题导入新授试一试练一练比一比总结教学目标
1.教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3. 使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验。教学重、难点
教学重点:感受“转化”策略的价值,会用“转化”的策略解决问题,丰富学生的策略意识。
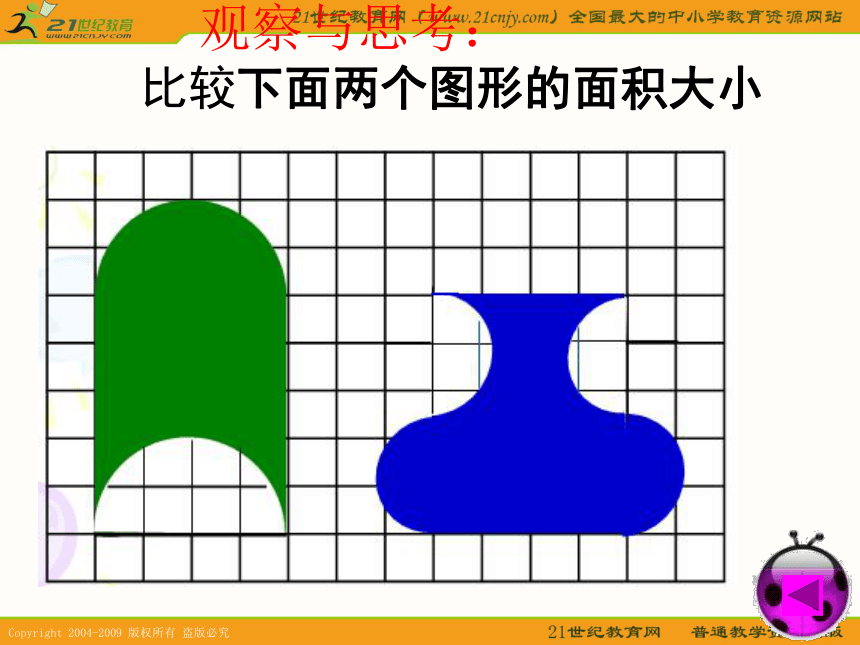
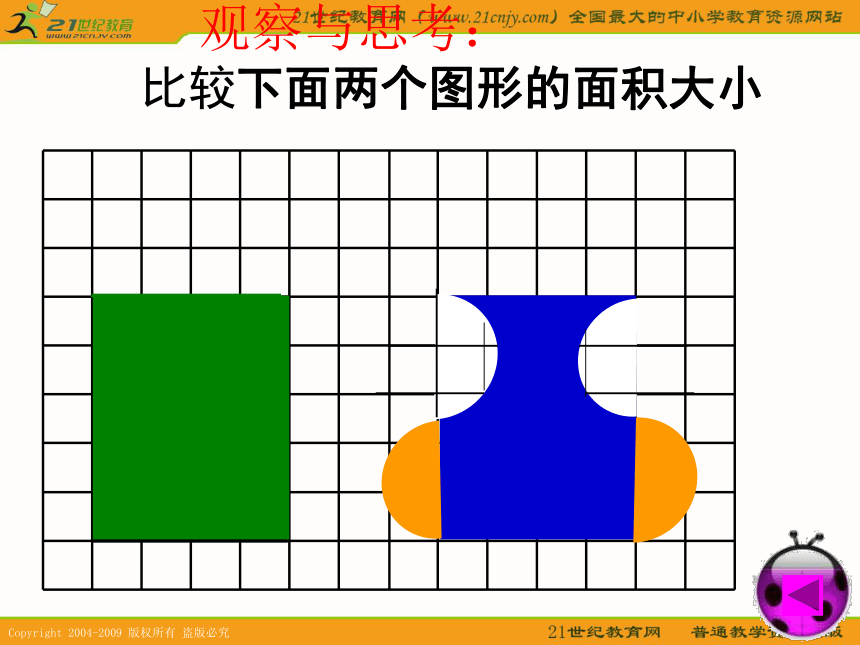
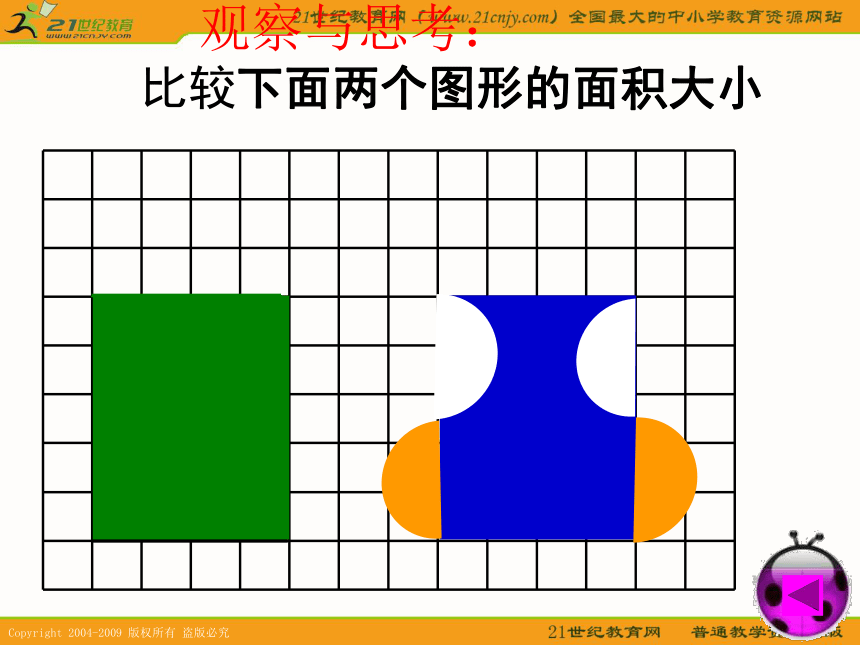
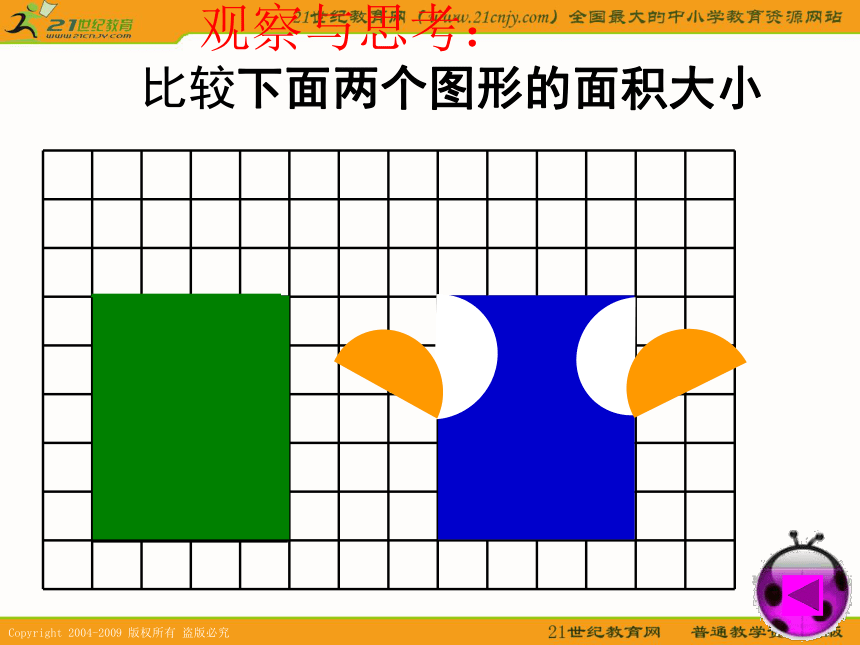
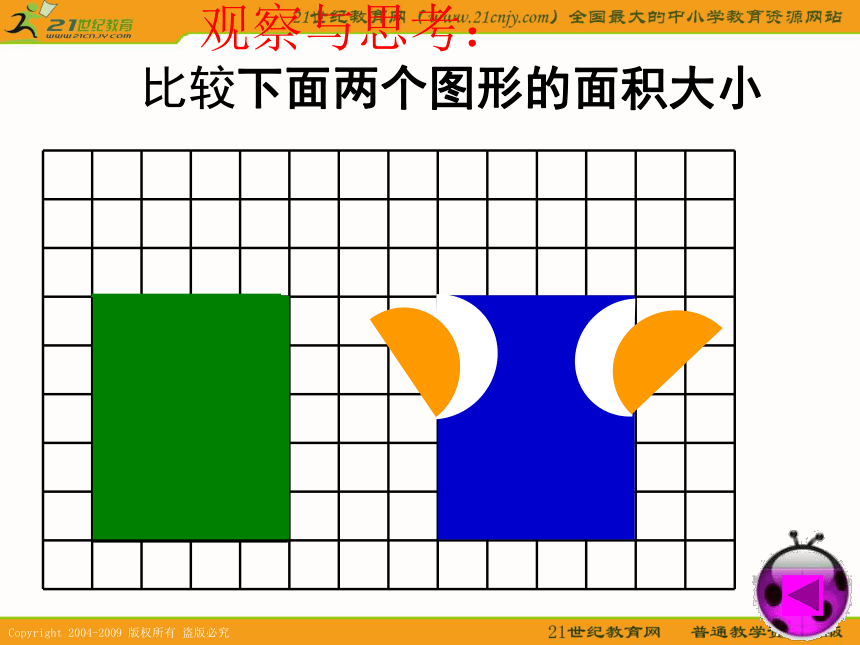
教学难点:掌握转化的方法和技巧,会用“转化”的策略解决问题。 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 回顾一下,我们曾经运用转化的策略解决过哪些图形问题?转化 推导平行四边形的面积公式时,把平行四边形转化成长方形。 计算圆柱的体积时,把圆柱转化成长方体。例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便? 每个小方格的边长是1cm,右边图形的周长是多少cm?例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便? 每个小方格的边长是1cm,右边图形的周长是多少cm?练一练用分数表示各图中的涂色部分上页试一试如图,正方形的边长是4厘米。E、F分别是BC和CD的中点,求阴影部分的面积。123比一比计算下面图形的周长
计算
计算
11×4=4(m)返回2 × ∏ × 4÷2 + ∏ × 4 =25.12(m)返回 森林考察队员小虎要穿越一片长3千米,宽2千米的长方形树林,这片树林的树只有柏树和桦树两种,且成行成列排列。小虎从西南角进入树林,每遇到一棵柏树就向东走,遇到一棵桦树就向北走,最后他从树林东北角走了出来。请问他一共走了多少千米?2森林探险 下图的蒙古包是由一个圆柱和一个圆锥组成。蒙古包所占的空间大约是多少立方米?28 m1.2 m2.1m22221、求阴影部分的面积。2厘米2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米32、比较下面两个图形的周长大小33 下面图是两个同样大的圆,半径为1厘米,而且两个阴影部分A、B的面积相等,那么图中长方形的面积是多少平方厘米? ABCD用转化的策略解决问题数学活动的实质就是思维的转化过程。
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
掌握转化的策略,对学好数学至关重要。 多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。 有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只灯泡的容积是多少。阿普顿是普林顿大学数学系高材生,又在德国深造了一年,数学素养相当不错。他拿着这只梨形的灯泡,打量了好半天,又特地找来皮尺,上下量了尺寸,画出了各种示意图,还列出了一道又一道的算式。一个钟头过去了。爱迪生着急了,跑来问他算出来了没有。“正算到一半。”阿普顿慌忙回答,豆大的汗珠从他的额角上滚了下来。“才算到一半?”爱迪生十分诧异,走近一看,哎呀,在阿普顿的面前,好几张白纸上写满了密密麻麻的算式。“何必这么复杂呢?”爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是我们所需要的容积。”
“哦!”阿普顿恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。用转化的策略解决问题用转化的策略解决问题!?新——旧复杂——简单教学后记本节课突出“四性”:即现实性、趣味性、思考性、开放性,以激发学生的兴趣和思考。又以培养学生运用所学知识解决实际问题的能力,培养学生的数学意识,培养学生的探索精神和创新能力为核心理念而设计的一堂课。为今后更高层次的创新而奠定基础。
分析本节课,纵观全程,既把平移,旋转运用到图形等积变化的问题中,又蕴涵探索图形面积公式的转化,还有计算小数乘法的和分数除法时的转化,还有数量关系之间的转化等。通过回忆和交流,意识到转化是经常使用的策略,从而主动应用转化的策略解决问题。基于此,于是采用以下步骤解决。一.创设情境,感知策略。二.合作交流,探究策略。三.拓展运用,提升策略。
1.教材让学生在直观的情境中想到转化,并应用图形的平移和旋转知识进行图形的等积,等周长的变形。
2.在解决实际问题过程中体会转化的含义和应用的手段,感受转化在解决这个问题时的价值。
3. 使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,主动克服在解决问题中遇到的困难,获得成功的体验。教学重、难点
教学重点:感受“转化”策略的价值,会用“转化”的策略解决问题,丰富学生的策略意识。
教学难点:掌握转化的方法和技巧,会用“转化”的策略解决问题。 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 观察与思考: 比较下面两个图形的面积大小 回顾一下,我们曾经运用转化的策略解决过哪些图形问题?转化 推导平行四边形的面积公式时,把平行四边形转化成长方形。 计算圆柱的体积时,把圆柱转化成长方体。例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便? 每个小方格的边长是1cm,右边图形的周长是多少cm?例:观察下面的两个图形,想一想,要求右边图形的周长,怎样计算比较简便? 每个小方格的边长是1cm,右边图形的周长是多少cm?练一练用分数表示各图中的涂色部分上页试一试如图,正方形的边长是4厘米。E、F分别是BC和CD的中点,求阴影部分的面积。123比一比计算下面图形的周长
计算
计算
11×4=4(m)返回2 × ∏ × 4÷2 + ∏ × 4 =25.12(m)返回 森林考察队员小虎要穿越一片长3千米,宽2千米的长方形树林,这片树林的树只有柏树和桦树两种,且成行成列排列。小虎从西南角进入树林,每遇到一棵柏树就向东走,遇到一棵桦树就向北走,最后他从树林东北角走了出来。请问他一共走了多少千米?2森林探险 下图的蒙古包是由一个圆柱和一个圆锥组成。蒙古包所占的空间大约是多少立方米?28 m1.2 m2.1m22221、求阴影部分的面积。2厘米2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米31、求阴影部分的面积。2厘米2厘米32、比较下面两个图形的周长大小33 下面图是两个同样大的圆,半径为1厘米,而且两个阴影部分A、B的面积相等,那么图中长方形的面积是多少平方厘米? ABCD用转化的策略解决问题数学活动的实质就是思维的转化过程。
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
掌握转化的策略,对学好数学至关重要。 多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。 有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只灯泡的容积是多少。阿普顿是普林顿大学数学系高材生,又在德国深造了一年,数学素养相当不错。他拿着这只梨形的灯泡,打量了好半天,又特地找来皮尺,上下量了尺寸,画出了各种示意图,还列出了一道又一道的算式。一个钟头过去了。爱迪生着急了,跑来问他算出来了没有。“正算到一半。”阿普顿慌忙回答,豆大的汗珠从他的额角上滚了下来。“才算到一半?”爱迪生十分诧异,走近一看,哎呀,在阿普顿的面前,好几张白纸上写满了密密麻麻的算式。“何必这么复杂呢?”爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是我们所需要的容积。”
“哦!”阿普顿恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。用转化的策略解决问题用转化的策略解决问题!?新——旧复杂——简单教学后记本节课突出“四性”:即现实性、趣味性、思考性、开放性,以激发学生的兴趣和思考。又以培养学生运用所学知识解决实际问题的能力,培养学生的数学意识,培养学生的探索精神和创新能力为核心理念而设计的一堂课。为今后更高层次的创新而奠定基础。
分析本节课,纵观全程,既把平移,旋转运用到图形等积变化的问题中,又蕴涵探索图形面积公式的转化,还有计算小数乘法的和分数除法时的转化,还有数量关系之间的转化等。通过回忆和交流,意识到转化是经常使用的策略,从而主动应用转化的策略解决问题。基于此,于是采用以下步骤解决。一.创设情境,感知策略。二.合作交流,探究策略。三.拓展运用,提升策略。
