六年级数学下册课件 用转化的策略解决问题 2(苏教版)
文档属性
| 名称 | 六年级数学下册课件 用转化的策略解决问题 2(苏教版) |  | |
| 格式 | rar | ||
| 文件大小 | 771.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-02 18:48:00 | ||
图片预览






文档简介
课件40张PPT。苏教版六年级数学下册教学目标 1.初步学会运用转化的策略分析问题,灵活确定解决问题的思路,并能根据问题的特点确定具体的转化方法,从而有效地解决问题。
2.通过回顾曾经运用转化策略解决问题的过程,感受转化策略的应用价值。
3.进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识。 在内蒙古,有兄弟俩都是剽悍的骑士。他们常常打赌看谁的马跑得快,结果是各有胜负,因而他们也觉得乏味了。 于是哥哥提议:“我们比一比谁的马第二个而不是第一个跑到终点。”
“好啊,比谁的马跑得慢!”弟弟爽块的答应了。
听说有这种奇异得比赛来了不少观众!
比赛开始,观众们一起呐喊着:
“一!二!三!……”
可是兄弟俩骑着马都一动不动。
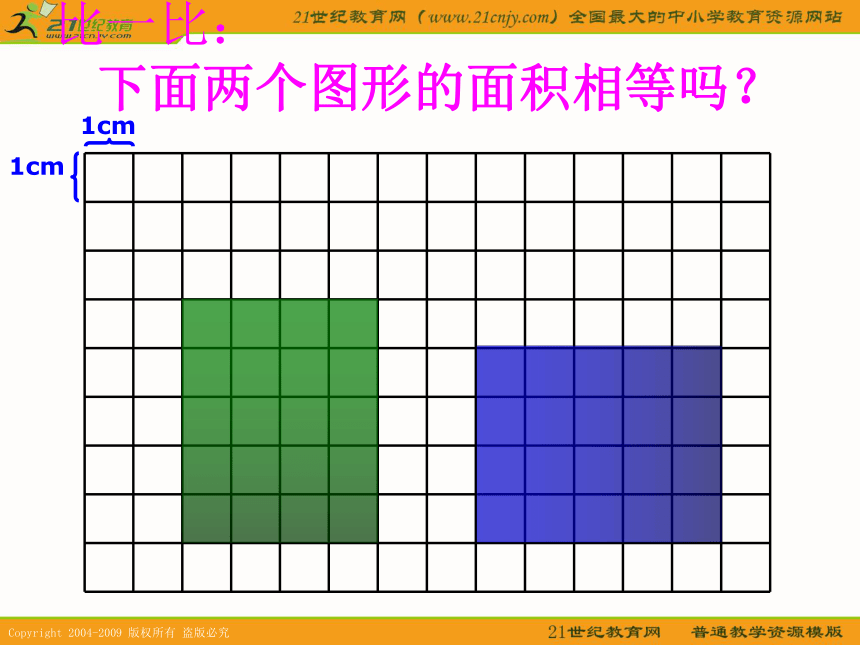
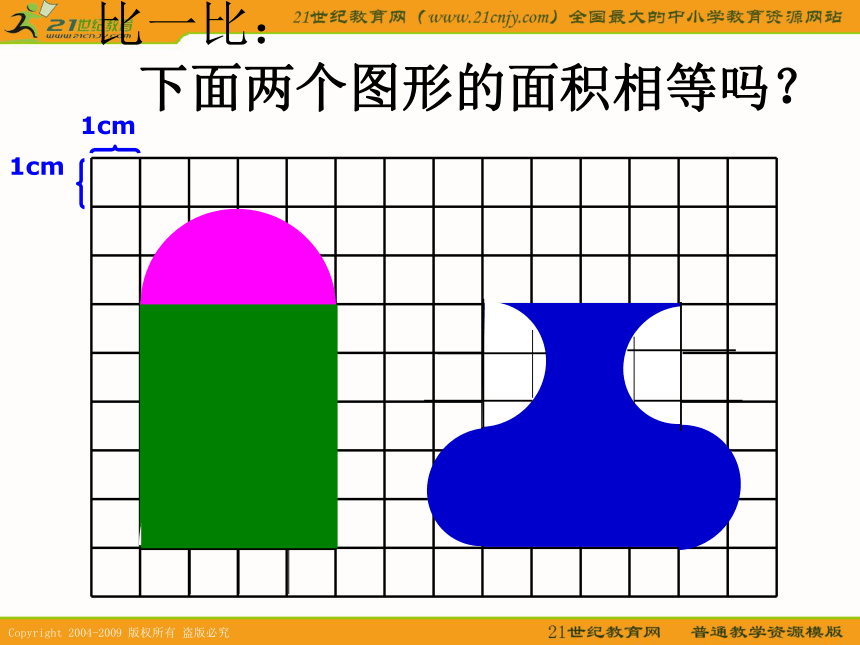
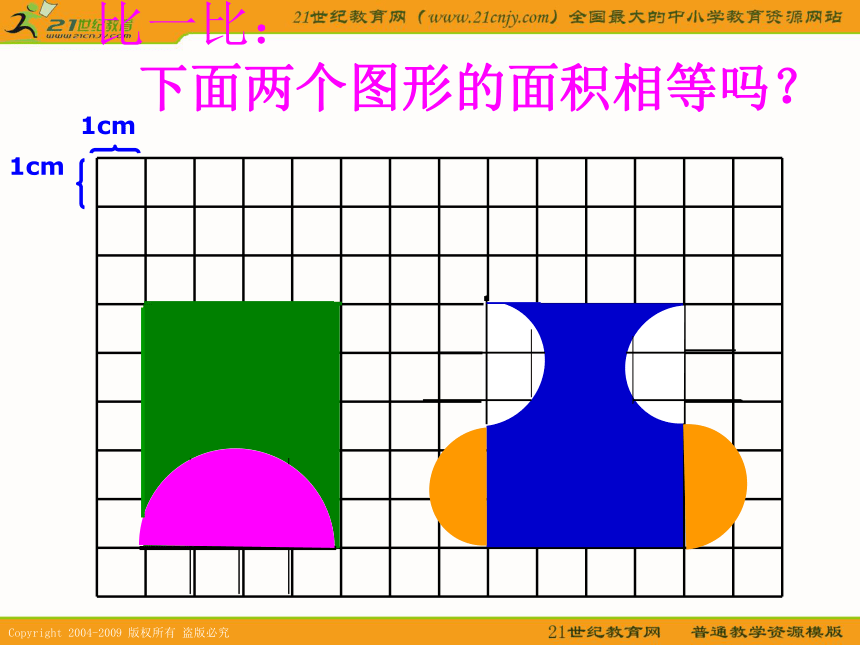
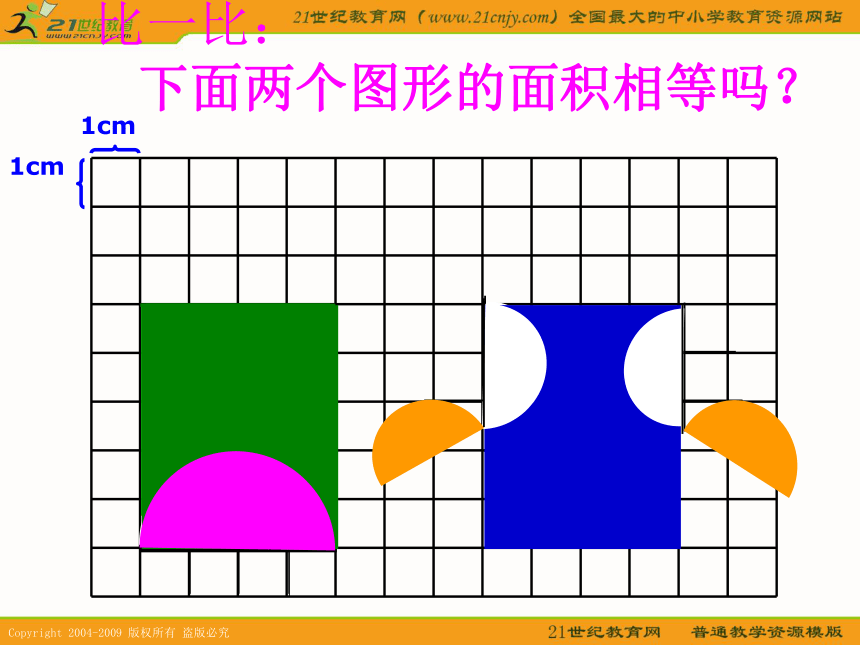
时间一分一秒的过去,两匹马还是一动不动……这样比要比到猴年马月?观众们议论纷纷,哄笑起来。比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm演示1演示2小结比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm返回马上试试用分数表示各图中的阴影部分。1cm1cm比一比: 下面两个图形的周长相等吗?周长马上试试O4cm1m计算下面图形的周长。AB1×4=4(m)周长是多少?返回黑:2×3.14×4÷2=12.56(cm)
红:3.14×4=12.56(cm)12.56+12.56=25.12(cm)4cm4cm返回2×3.14×4=25.12(cm)
返回4cmo.
回顾一下:在我们学过的图形问题中哪些地方还运用到了转化的策略?
s平s三s圆v柱计算推导平行四边形的面积公式时,把平行四边形转化成长方形。推导平行四边形的面积公式时,把平行四边形转化成长方形。返回 推导三角形的面积公式时,把三角形转化成平行四边形。 推导三角形的面积公式时,把三角形转化成平行四边形。 计算圆的面积时,把圆转化成长方形。12345678910111213141516 计算圆柱的体积时,把圆柱转化成长方体。1.7×1.4 = 异分母分数
转化
同分母分数小数乘法 转化 整数乘法 分数除法
转化
分数乘法巧计算这是一道展示你聪明才智的计算题++1 =庄子说:一尺之棰(木棍),日取其半,万世不竭。 有16支足球队参加比赛,比赛以单场淘汰制(即每场比赛淘汰1支球队)进行。一共要进行多少场比赛后才能产生冠军?848+4+2+1=15 (场) 有16支足球队参加比赛,比赛以单场淘汰制进行。一共要进行多少场比赛后才能产生冠军?
16-1=15 (场) 如果有64支球队参加比赛,产 生冠军要比赛多少场?(淘汰多少支球队?)如果有N支球队参加比赛,产 生冠军要比赛多少场? 有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只梨形灯泡的容积是多少……
一个钟头过去了,才算到一半
“何必这么复杂呢?”爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是灯泡的容积。”
“哦!”阿普顿恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。用转化的策略解决问题用转化的策略解决问题 多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。”!? 小洪把一杯纯牛奶喝掉 ,加满水, 摇匀,喝掉 ,加满水,摇匀,再喝 掉 ,再加满水,最后整杯喝掉。请 问,喝的水多,还是牛奶多?用分数表示各图中的涂色部分上页2×23×31+3+5返回1+3+5+7+9+11+74
×
4+95
×
5+116
×
6=36
2.通过回顾曾经运用转化策略解决问题的过程,感受转化策略的应用价值。
3.进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识。 在内蒙古,有兄弟俩都是剽悍的骑士。他们常常打赌看谁的马跑得快,结果是各有胜负,因而他们也觉得乏味了。 于是哥哥提议:“我们比一比谁的马第二个而不是第一个跑到终点。”
“好啊,比谁的马跑得慢!”弟弟爽块的答应了。
听说有这种奇异得比赛来了不少观众!
比赛开始,观众们一起呐喊着:
“一!二!三!……”
可是兄弟俩骑着马都一动不动。
时间一分一秒的过去,两匹马还是一动不动……这样比要比到猴年马月?观众们议论纷纷,哄笑起来。比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm演示1演示2小结比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm比一比: 下面两个图形的面积相等吗?1cm1cm返回马上试试用分数表示各图中的阴影部分。1cm1cm比一比: 下面两个图形的周长相等吗?周长马上试试O4cm1m计算下面图形的周长。AB1×4=4(m)周长是多少?返回黑:2×3.14×4÷2=12.56(cm)
红:3.14×4=12.56(cm)12.56+12.56=25.12(cm)4cm4cm返回2×3.14×4=25.12(cm)
返回4cmo.
回顾一下:在我们学过的图形问题中哪些地方还运用到了转化的策略?
s平s三s圆v柱计算推导平行四边形的面积公式时,把平行四边形转化成长方形。推导平行四边形的面积公式时,把平行四边形转化成长方形。返回 推导三角形的面积公式时,把三角形转化成平行四边形。 推导三角形的面积公式时,把三角形转化成平行四边形。 计算圆的面积时,把圆转化成长方形。12345678910111213141516 计算圆柱的体积时,把圆柱转化成长方体。1.7×1.4 = 异分母分数
转化
同分母分数小数乘法 转化 整数乘法 分数除法
转化
分数乘法巧计算这是一道展示你聪明才智的计算题++1 =庄子说:一尺之棰(木棍),日取其半,万世不竭。 有16支足球队参加比赛,比赛以单场淘汰制(即每场比赛淘汰1支球队)进行。一共要进行多少场比赛后才能产生冠军?848+4+2+1=15 (场) 有16支足球队参加比赛,比赛以单场淘汰制进行。一共要进行多少场比赛后才能产生冠军?
16-1=15 (场) 如果有64支球队参加比赛,产 生冠军要比赛多少场?(淘汰多少支球队?)如果有N支球队参加比赛,产 生冠军要比赛多少场? 有一次,爱迪生把一只灯泡交给他的助手阿普顿,让他计算一下这只梨形灯泡的容积是多少……
一个钟头过去了,才算到一半
“何必这么复杂呢?”爱迪生微笑着说,“你把这只灯泡装满水,再把水倒在量杯里,量杯量出来的水的体积,就是灯泡的容积。”
“哦!”阿普顿恍然大悟。他飞快地跑进实验室,不到1分钟,没有经过任何运算,就把灯泡的容积准确地求出来了。用转化的策略解决问题用转化的策略解决问题 多位数学家说过:“什么叫解题?解题就是把题目转化为已经解过的题。”!? 小洪把一杯纯牛奶喝掉 ,加满水, 摇匀,喝掉 ,加满水,摇匀,再喝 掉 ,再加满水,最后整杯喝掉。请 问,喝的水多,还是牛奶多?用分数表示各图中的涂色部分上页2×23×31+3+5返回1+3+5+7+9+11+74
×
4+95
×
5+116
×
6=36
