苏教版六年级下册数学面积的变化 课件(共16张PPT)
文档属性
| 名称 | 苏教版六年级下册数学面积的变化 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 420.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-29 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
变变会啊化 德
面积的变化
苏教版六年级数学下册
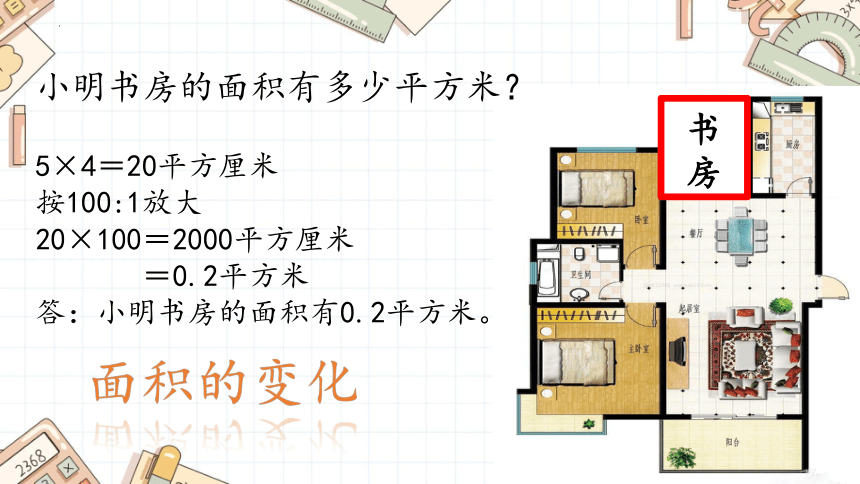
小明书房的面积有多少平方米?
面积的变化
5×4=20平方厘米
按100:1放大
20×100=2000平方厘米
=0.2平方米
答:小明书房的面积有0.2平方米。
书
房
学习目标:
1.结合具体的实例,探索并发现平面图形按比例放大后面积的变化规律。
2.加深对图形放大与缩小的含义以及比例意义的理解。
2.在经历探索规律的过程中,积累观察、比较、分析、概括、归纳等活动经验,感悟由特殊到一般的归纳思想,发展数学思维。
提出问题
下面的大长方形是小长方形按比例放大得到的。
1.分别量出它们的长和宽,写出对应边长的比?
2.分别计算面积,求出大长方形与小长方形面积比?
活动一:组学(限时4分钟)
1.独立完成 【学习任务一】
2.完成后在小组内交流自己的想法。
3.小组汇报交流成果。
提出问题
其它平面图形按比例放大后,
面积的比又会怎样变化呢
这其中会不会蕴含着什么规律呢?
大长方形与小长方形的
长度的比是( 3):( 1),
面积的比是( 9):( 1)。
观察这两个比,这两个比有什么关系?
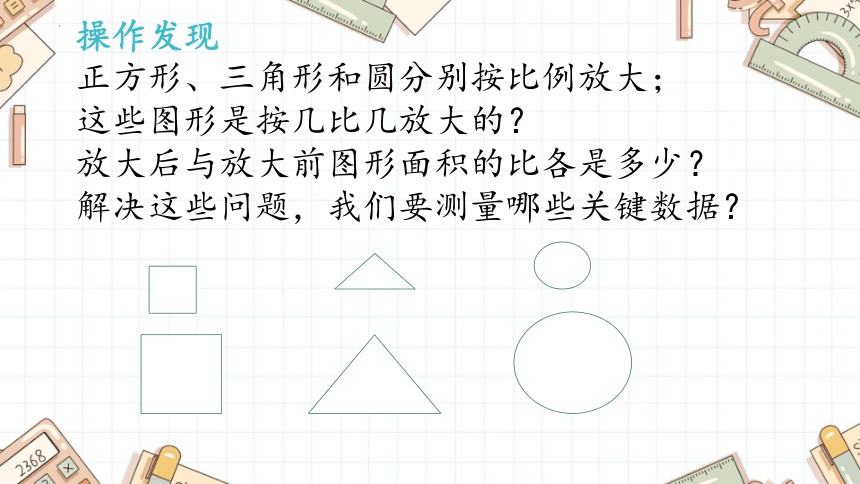
正方形、三角形和圆分别按比例放大;
这些图形是按几比几放大的?
放大后与放大前图形面积的比各是多少?
解决这些问题,我们要测量哪些关键数据?
操作发现
放大前 放大后 放大后与放大前的比
正方形 边长/cm
面积/cm2
三角形 底/cm
高/cm
面积/cm2
圆 半径/cm
面积/cm2
请同学们通过测量和计算,把下表填写完整。
操作发现
活动二:组学(限时5分钟)
1.独立完成 【学习任务二】
(1)计算放大后与放大前的面积。
(2)放大后与放大前图形的长度比各是几比几?
放大后与放大前图形面积的比各是几比几?
(3)把数据填入表格中。
2.完成后在小组内交流自己的想法。
3.在组长安排下进行小组汇报。
操作发现
小对子讨论: 比较每个图形放大后与放大前的长度比和面积比,你能发现什么规律?
两个比的后项都是1,面积比的前项是长度比前项的平方。
长度比是2:1,面积比是4:1;
长度比是3:1,面积比是9:1;
长度比是4:1,面积比是16:1…
如果把一个图形按n:1的比放大,就是放大后与放大前图形的长度比是( ):( ),那么放大后与放大前图形的面积比是( ):( )。
得出结论
活动三:组学(限时4分钟)
1.独立完成 【学习任务三】
(1)在方格纸上画一个平行四边形(1格表示1厘米),小组成员分别按不同比例放大。
(2)放大后与放大前图形的长度比、面积比。
(3)看看是不是符合上面发现的规律。
2.完成后在小组内交流自己的想法。
3.小组长进行汇报。
验证规律
平面图中小明的书房按100:1放大后,书房的面积有多少平方米?
解决问题
5×4=20平方厘米
按100:1放大,放大后与放大前的面积比是10000:1。
20×10000=200000平方厘米
=20平方米
答:小明书房的面积有20平方米。
书 房
4cm
5cm
同学们: 回顾探索规律的过程,你有什么收获?
收获
扩展延伸
课后作业
谢谢!
变变会啊化 德
面积的变化
苏教版六年级数学下册
小明书房的面积有多少平方米?
面积的变化
5×4=20平方厘米
按100:1放大
20×100=2000平方厘米
=0.2平方米
答:小明书房的面积有0.2平方米。
书
房
学习目标:
1.结合具体的实例,探索并发现平面图形按比例放大后面积的变化规律。
2.加深对图形放大与缩小的含义以及比例意义的理解。
2.在经历探索规律的过程中,积累观察、比较、分析、概括、归纳等活动经验,感悟由特殊到一般的归纳思想,发展数学思维。
提出问题
下面的大长方形是小长方形按比例放大得到的。
1.分别量出它们的长和宽,写出对应边长的比?
2.分别计算面积,求出大长方形与小长方形面积比?
活动一:组学(限时4分钟)
1.独立完成 【学习任务一】
2.完成后在小组内交流自己的想法。
3.小组汇报交流成果。
提出问题
其它平面图形按比例放大后,
面积的比又会怎样变化呢
这其中会不会蕴含着什么规律呢?
大长方形与小长方形的
长度的比是( 3):( 1),
面积的比是( 9):( 1)。
观察这两个比,这两个比有什么关系?
正方形、三角形和圆分别按比例放大;
这些图形是按几比几放大的?
放大后与放大前图形面积的比各是多少?
解决这些问题,我们要测量哪些关键数据?
操作发现
放大前 放大后 放大后与放大前的比
正方形 边长/cm
面积/cm2
三角形 底/cm
高/cm
面积/cm2
圆 半径/cm
面积/cm2
请同学们通过测量和计算,把下表填写完整。
操作发现
活动二:组学(限时5分钟)
1.独立完成 【学习任务二】
(1)计算放大后与放大前的面积。
(2)放大后与放大前图形的长度比各是几比几?
放大后与放大前图形面积的比各是几比几?
(3)把数据填入表格中。
2.完成后在小组内交流自己的想法。
3.在组长安排下进行小组汇报。
操作发现
小对子讨论: 比较每个图形放大后与放大前的长度比和面积比,你能发现什么规律?
两个比的后项都是1,面积比的前项是长度比前项的平方。
长度比是2:1,面积比是4:1;
长度比是3:1,面积比是9:1;
长度比是4:1,面积比是16:1…
如果把一个图形按n:1的比放大,就是放大后与放大前图形的长度比是( ):( ),那么放大后与放大前图形的面积比是( ):( )。
得出结论
活动三:组学(限时4分钟)
1.独立完成 【学习任务三】
(1)在方格纸上画一个平行四边形(1格表示1厘米),小组成员分别按不同比例放大。
(2)放大后与放大前图形的长度比、面积比。
(3)看看是不是符合上面发现的规律。
2.完成后在小组内交流自己的想法。
3.小组长进行汇报。
验证规律
平面图中小明的书房按100:1放大后,书房的面积有多少平方米?
解决问题
5×4=20平方厘米
按100:1放大,放大后与放大前的面积比是10000:1。
20×10000=200000平方厘米
=20平方米
答:小明书房的面积有20平方米。
书 房
4cm
5cm
同学们: 回顾探索规律的过程,你有什么收获?
收获
扩展延伸
课后作业
谢谢!
