人教版六年级上册数学数学广角—数与形+运用数形结合发现规律 课件(共20张PPT)
文档属性
| 名称 | 人教版六年级上册数学数学广角—数与形+运用数形结合发现规律 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-29 09:05:13 | ||
图片预览




文档简介
(共20张PPT)
人教版数学六年级(上)
第1课时 运用数形结合发现规律
数学广角——数与形
8
数形结合思想是学习数学的一种重要
思想,运用数形结合的方法,探究数
学规律,可以使数学问题解决起来更
简单。
数与形
学习目标
在解决数学问题的过程中,体会和掌握数形结合、归纳推理等基本的数学思想。
能够借助“形”来直观感受“形”与“数”之间
的关系,解决与“数”有关的实际问题。
体会数与形的联系,进一步积累数形结合数学活动经验,培养学生数形结合的数学思想意识;
请同学们用最快的速度计算下面的算式的结果。
1+3+5+7+9+11+13+…+99=?
超级神算:只要从1开始的连续奇数相加,我都能脱口而出,你相信吗?
1+3=( )
4
1+3 +5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+11+13+15+17+19=( )
100
你发现了什么?
从1开始的连续奇数相加的和,正好是这些奇数的个数的平方。
计算出结果。
2个奇数相加
3个奇数相加
4个奇数相加
10个奇数相加
想一想,说一说:在刚才的计算中,你发现了什么?
你能发现其中的规律吗?这节课我们学习数形结合的方法,使你能更快地发现规律,更容易地进行计算。
算式右边分别是2、3、4……的平方
算式左边是连续的奇数相加。
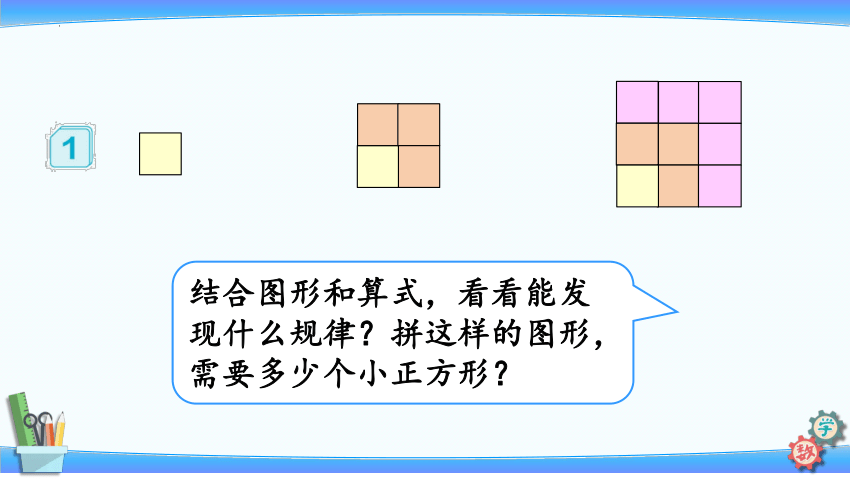
结合图形和算式,看看能发现什么规律?拼这样的图形,需要多少个小正方形?
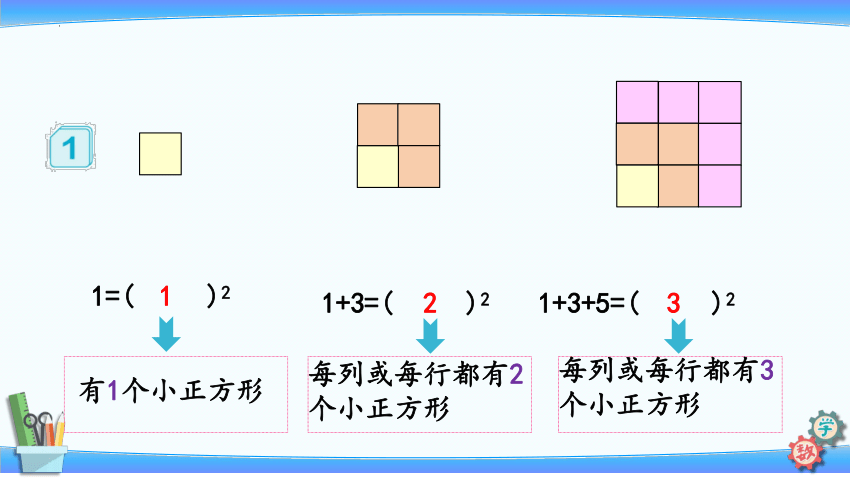
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
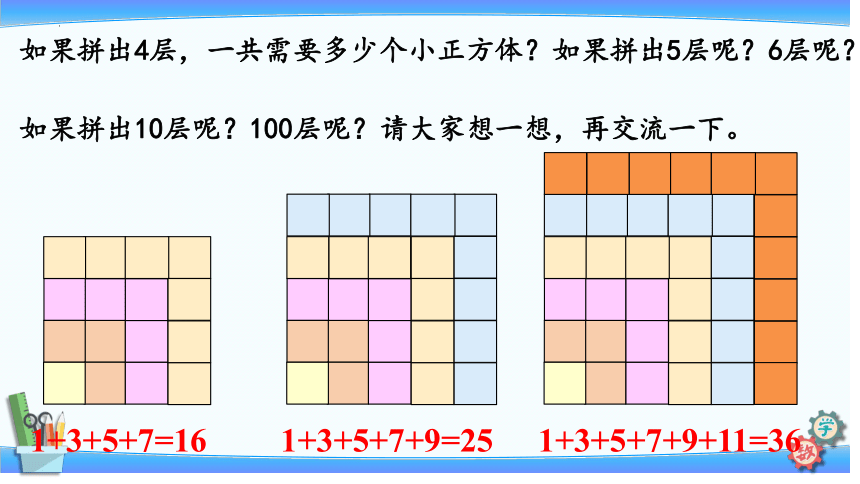
如果拼出4层,一共需要多少个小正方体?如果拼出5层呢?6层呢?
1+3+5+7=16
1+3+5+7+9=25
1+3+5+7+9+11=36
如果拼出10层呢?100层呢?请大家想一想,再交流一下。
从1开始,5个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,10个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,15个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
25
100
225
我发现,算式左边的加数是每个正方形图左下角的小正方形和其他“ ”形图中所包含的小正方形个数之和,正好等于每个正方形图中每行或列小正方形个数的平方。
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
课堂练习
请你根据例1的结论算一算。
1+3+5+7+9+11+13+11+9+7+5+3+1=
+
= 85
1+3+5+7+5+3+1 =( )
25
72
62
72
62
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?。
做一做
绿色:
1
2
3
4
蓝色:
8
10
12
14
照这样画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
6
18
10
26
绿色
蓝色
绿色 1 2 3 4 … 6 … 10
蓝色 8 10 12 14 … 18 … 26
5
16
n
2(n+3)
道理:第n个图形有n个红色小正方形,有2(n+3)个蓝色小正方形。
白色:_____ ______ ______ ______
黑色:_____ ______ ______ ______
1.下面每个图形中各有多少个白色小正方形和多少个灰色小正方形
作业设计
1
4
4
8
9
12
16
16
照这样接着画下去,第n个图形中有( )个白色小正方形和( )个灰色小正方形。
n2
4n
2.下面每个图中最外圈有多少个小正方形?
照这样画下去,第5个图形最外圈有( )个小正方形。
40
3 -1=8
2
5 -3 =16
2
2
7 -5 =24
2
2
11 -9 =40
2
2
你能解释其中的道理吗?
第n(n>0)图形最外圈有
(2n+1)-(2n-1)=8n(个)小正方形。
2
2
3. 按照规律接着画一画、填一填。
3
1
6
10
1+2
1+2+3
1+2+3+4
1
2
3
4
图的个数
图里圆的个数
如果不画,你知道第8个图有几个圆吗?第18个?第35个呢?
发现1:画第几个图,就是在前一个图的基础上加几,如第4个图,就是在前一个图上再加4;
发现2:画到第n个图,这个图里圆的个数就是1+2+3+…+n。比如画到第3个图时,这个图里的个数就是1+2+3,画到第5个图时,这个图里圆的个数就是1+2+3+4+5。
4.照这样画下去,第50个图形有( )个这样的小黑点。
2500
第几个图形,小黑点的个数就是几的平方,即第50个图形,就有2500个小黑点。
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
人教版数学六年级(上)
第1课时 运用数形结合发现规律
数学广角——数与形
8
数形结合思想是学习数学的一种重要
思想,运用数形结合的方法,探究数
学规律,可以使数学问题解决起来更
简单。
数与形
学习目标
在解决数学问题的过程中,体会和掌握数形结合、归纳推理等基本的数学思想。
能够借助“形”来直观感受“形”与“数”之间
的关系,解决与“数”有关的实际问题。
体会数与形的联系,进一步积累数形结合数学活动经验,培养学生数形结合的数学思想意识;
请同学们用最快的速度计算下面的算式的结果。
1+3+5+7+9+11+13+…+99=?
超级神算:只要从1开始的连续奇数相加,我都能脱口而出,你相信吗?
1+3=( )
4
1+3 +5=( )
9
1+3+5+7=( )
16
1+3+5+7+9+11+13+15+17+19=( )
100
你发现了什么?
从1开始的连续奇数相加的和,正好是这些奇数的个数的平方。
计算出结果。
2个奇数相加
3个奇数相加
4个奇数相加
10个奇数相加
想一想,说一说:在刚才的计算中,你发现了什么?
你能发现其中的规律吗?这节课我们学习数形结合的方法,使你能更快地发现规律,更容易地进行计算。
算式右边分别是2、3、4……的平方
算式左边是连续的奇数相加。
结合图形和算式,看看能发现什么规律?拼这样的图形,需要多少个小正方形?
1=( )2
1+3=( )2
1+3+5=( )2
1
2
3
每列或每行都有2个小正方形
每列或每行都有3个小正方形
有1个小正方形
如果拼出4层,一共需要多少个小正方体?如果拼出5层呢?6层呢?
1+3+5+7=16
1+3+5+7+9=25
1+3+5+7+9+11=36
如果拼出10层呢?100层呢?请大家想一想,再交流一下。
从1开始,5个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,10个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
从1开始,15个连续奇数的小正方形组成的大正方形里,有几个这样的小正方形?
25
100
225
我发现,算式左边的加数是每个正方形图左下角的小正方形和其他“ ”形图中所包含的小正方形个数之和,正好等于每个正方形图中每行或列小正方形个数的平方。
我发现,从1开始的连续奇数的和正好是这串数个数的平方。
课堂练习
请你根据例1的结论算一算。
1+3+5+7+9+11+13+11+9+7+5+3+1=
+
= 85
1+3+5+7+5+3+1 =( )
25
72
62
72
62
可以看成两部分:1+3+5+7=42
5+3+1= 32
42+ 32 =25
下面每个图中各有多少个绿色小正方形和多少个蓝色小正方形?。
做一做
绿色:
1
2
3
4
蓝色:
8
10
12
14
照这样画下去,第6个图形有多少个绿色小正方形和多少个蓝色小正方形?第10个图形呢?你能解释这其中的道理吗?
6
18
10
26
绿色
蓝色
绿色 1 2 3 4 … 6 … 10
蓝色 8 10 12 14 … 18 … 26
5
16
n
2(n+3)
道理:第n个图形有n个红色小正方形,有2(n+3)个蓝色小正方形。
白色:_____ ______ ______ ______
黑色:_____ ______ ______ ______
1.下面每个图形中各有多少个白色小正方形和多少个灰色小正方形
作业设计
1
4
4
8
9
12
16
16
照这样接着画下去,第n个图形中有( )个白色小正方形和( )个灰色小正方形。
n2
4n
2.下面每个图中最外圈有多少个小正方形?
照这样画下去,第5个图形最外圈有( )个小正方形。
40
3 -1=8
2
5 -3 =16
2
2
7 -5 =24
2
2
11 -9 =40
2
2
你能解释其中的道理吗?
第n(n>0)图形最外圈有
(2n+1)-(2n-1)=8n(个)小正方形。
2
2
3. 按照规律接着画一画、填一填。
3
1
6
10
1+2
1+2+3
1+2+3+4
1
2
3
4
图的个数
图里圆的个数
如果不画,你知道第8个图有几个圆吗?第18个?第35个呢?
发现1:画第几个图,就是在前一个图的基础上加几,如第4个图,就是在前一个图上再加4;
发现2:画到第n个图,这个图里圆的个数就是1+2+3+…+n。比如画到第3个图时,这个图里的个数就是1+2+3,画到第5个图时,这个图里圆的个数就是1+2+3+4+5。
4.照这样画下去,第50个图形有( )个这样的小黑点。
2500
第几个图形,小黑点的个数就是几的平方,即第50个图形,就有2500个小黑点。
这节课你们都学会了哪些知识?
1.把图形与算式结合起来,是发现规律的关键。
2.从1开始的连续几个奇数的和与正方形数的关系,即有几个连续奇数相加,每边小正方形个数就是几的平方。
