贵州省毕节市金沙县2024-2025学年八年级下学期期末考试数学模拟练习卷(含答案)
文档属性
| 名称 | 贵州省毕节市金沙县2024-2025学年八年级下学期期末考试数学模拟练习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 381.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 10:29:00 | ||
图片预览


文档简介
贵州省毕节市金沙县2024-2025学年八年级下学期期末考试数学模拟练习卷
一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
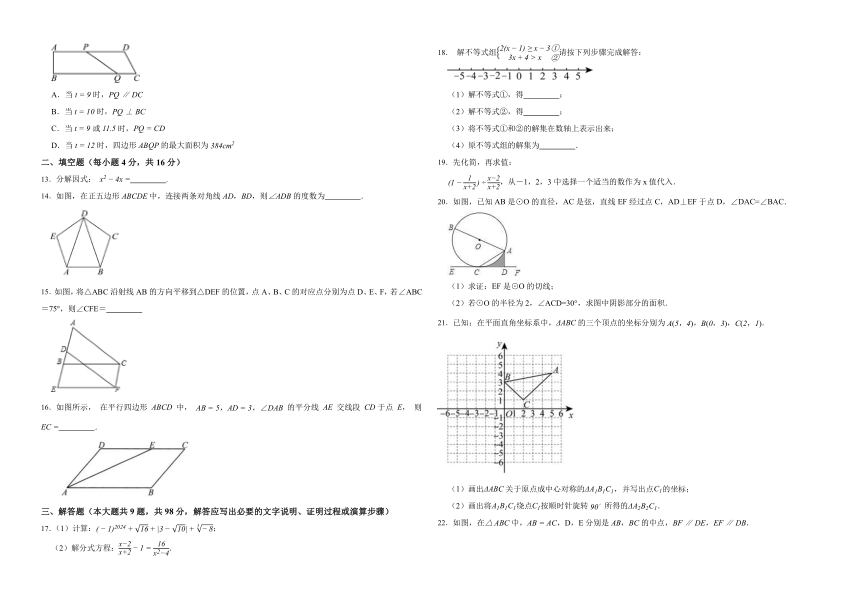
1.下列图形中,是中心对称图形的是 ( )
A. B.
C. D.
2.如图,数轴上的点与点所表示的数分别为a,b,则下列不等式成立的是( )
A.a-2>b-2 B. C. D.
3.要使分式有意义,则x的取值应满足( )
A. B. C. D.
4.下列各式计算正确的是( )
A. B.
C. D.
5.在平面直角坐标系中,点先向左平移3个单位,再向上平移5个单位后得到的点的坐标为( )
A. B. C. D.
6.将不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
7.如图所示,中,,将绕点顺时针旋转得到,使点的对应点落在边上,连接,则的度数为( )
A. B. C. D.
8.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点,则根据图象可知关于x的不等式的解集是( )
A. B. C. D.
9.A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C.+4=9 D.
10.已知关于x的分式方程的解是非负数,则m的取值范围是( )
A. B.
C.且 D.且
11.如图,已知直线,,,那么的大小为( )
A.80° B.70° C.90° D.100°
12.如图,四边形中,,.点从点A出发,以的速度向点D运动;点从点C同时出发,以的速度向点B运动.规定其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为秒,下列结论错误的是( )
A.当时,
B.当时,
C.当或时,
D.当时,四边形的最大面积为
二、填空题(每小题4分,共16分)
13.分解因式: .
14.如图,在正五边形中,连接两条对角线,,则的度数为 .
15.如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
16.如图所示, 在平行四边形 中, 的平分线 交线段 于点 , 则 .
三、解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(1)计算:;
(2)解分式方程:.
18. 解不等式组请按下列步骤完成解答:
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)将不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为 .
19.先化简,再求值:
,从-1,2,3中选择一个适当的数作为x值代入.
20.如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
21.已知:在平面直角坐标系中,的三个顶点的坐标分别为,,.
(1)画出关于原点成中心对称的,并写出点的坐标;
(2)画出将绕点按顺时针旋转所得的.
22.如图,在中,,D,E分别是,的中点,,.
(1)求证:四边形是菱形;
(2)连接交于点M,连接,若,,求,的长.
23. 如图,在中,过中点的直线分别交,的延长线于点,.
(1)求证:;
(2)连结,若,,的周长为16,求的周长.
24.如图,一次函数的图象与反比例函数的图象交于点,.
(1)求反比例函数和一次函数的解析式;
(2)利用图象,直接写出不等式的解集为 ;
(3)在轴上找一点,使△的周长最小,并求出最小值.
25.综合与实践
特例感知:
如图,在等边三角形中,是延长线上一点,且,以为边作等边三角形,连接,分别过点作,过点作,交于点,连接,与交于点.
(1)试判断和的数量关系,并说明理由.
(2)猜想论证:
将绕点按顺时针方向旋转一定角度得到图,则中和的数量关系是否仍然成立?请说明理由.
(3)拓展延伸:
将如图所示的绕点按逆时针方向旋转角度,当时,请直接写出的值.
参考答案
1.B
2.C
3.B
4.D
5.C
6.A
7.C
8.C
9.A
10.D
11.A
12.C
13.
14.
15.105°
16.2
17.(1)解:原式
;
(2)解:方程两边同时乘x2-4,得,
解得:,
经检验,不是原分式方程的解,
原分式方程无解.
18.(1)
(2)
(3)
(4)
19.解:
=,
∵当x+2≠0且x﹣2≠0,即x≠﹣2且x≠2时分式有意义,
∴取x=3,
当x=3时,原式==4.
20.(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥EF,
∴OC⊥EF,
则EF为圆O的切线;
(2)解:∵∠ACD=30°,∠ADC=90°,
∴∠CAD=∠OCA=60°,
∴△AOC为等边三角形,
∴AC=OC=OA=2,
在Rt△ACD中,∠ACD=30°,
∴AD=AC=1,根据勾股定理得:CD=,
∴S阴影=S△ACD-(S扇形AOC-S△AOC)=×1×-()=.
21.(1)解:如图所示,
∴即为所求,其中点的坐标为.
(2)解:如图所示,
∴即为所求
22.(1)证明:∵,,
∴四边形是平行四边形,
∵,
∴,
∵D,E分别是,的中点,
∴是的中位线,,
∴,
∴,
∴四边形是菱形;
(2)解:如图所示:
∵四边形是菱形,
∴,,
∴,
是的中位线,
∴,,
在中,,
在中,,
∴.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,AD=BC,AD∥BC,
∴∠OAF=∠OCE,∠F=∠E,
在和中,
,
∴,
∴AF=CE,
∴CE-BC=AF-AD,
∴BE=DF;
(2)解:如图,连接CF,
∵EF⊥AC,AO=CO,
∴EF垂直平分AC,
∴AF=CF,
∵,,
∴2+DC+AF=16,
∴2+DC+AD+DF=2+DC+AD+2=4+DC+AD=16,
∴DC+AD=12,
∴的周长为2(DC+AD)=2×12=24.
24.(1)解:反比例函数的图象经过,
,
解得,
反比例函数的解析式为;
在中,当时,,
,
一次函数的图象与反比例函数的图象交于点,,
,
解得,
一次函数解析式为
(2)
(3)解:如图所示,作点关于轴的对称点,连接,,,,则,
由轴对称的性质可得,
,,
,
△的周长,
当有最小值时,△的周长有最小值,
,
当有最小值时,△的周长有最小值,
,
当、、三点共线时,有最小值,即此时△的周长有最小值,最小值为,
,,
,
△的周长的最小值为;
设直线解析式为,
则,
,
直线解析式为,
在中,当时,,
;
综上所述,当点的坐标为时,△的周长有最小值,最小值为.
25.(1)解:,理由如下:
和都是等边三角形,
,,,
,
,
,
,
,
,,
四边形是平行四边形,
,
,
在和中,
,
∴,
;
(2)解:仍然成立,理由如下:
如图,延长,交于,
和都是等边三角形,
,,,
,
,
,
,
,
,,
四边形是平行四边形,
,
,
在和中,
,
∴,
;
(3)解:①当α<90°,如图,延长,交ED的延长线于,
和都是等边三角形,
∴∠ABC=∠CDE=60°,
∵∠ABF=90°,
,
,
,
∵∠CDE=∠R+∠DCR,
,
,
②如图,延长交于,
由上知:,,
∵∠CED=∠CWE+∠WCE,
,
,
,
综上所述:或.
一、选择题(每小题3分,共36分.每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在答题卡相应位置填涂)
1.下列图形中,是中心对称图形的是 ( )
A. B.
C. D.
2.如图,数轴上的点与点所表示的数分别为a,b,则下列不等式成立的是( )
A.a-2>b-2 B. C. D.
3.要使分式有意义,则x的取值应满足( )
A. B. C. D.
4.下列各式计算正确的是( )
A. B.
C. D.
5.在平面直角坐标系中,点先向左平移3个单位,再向上平移5个单位后得到的点的坐标为( )
A. B. C. D.
6.将不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
7.如图所示,中,,将绕点顺时针旋转得到,使点的对应点落在边上,连接,则的度数为( )
A. B. C. D.
8.数形结合是解决数学问题常用的思想方法.如图,直线和直线相交于点,则根据图象可知关于x的不等式的解集是( )
A. B. C. D.
9.A,B两地相距48千米,一艘轮船从A地顺流航行至B地,又立即从B地逆流返回A地,共用去9小时,已知水流速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则可列方程( )
A. B.
C.+4=9 D.
10.已知关于x的分式方程的解是非负数,则m的取值范围是( )
A. B.
C.且 D.且
11.如图,已知直线,,,那么的大小为( )
A.80° B.70° C.90° D.100°
12.如图,四边形中,,.点从点A出发,以的速度向点D运动;点从点C同时出发,以的速度向点B运动.规定其中一个动点到达终点时,另一个动点也随之停止运动,设运动时间为秒,下列结论错误的是( )
A.当时,
B.当时,
C.当或时,
D.当时,四边形的最大面积为
二、填空题(每小题4分,共16分)
13.分解因式: .
14.如图,在正五边形中,连接两条对角线,,则的度数为 .
15.如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
16.如图所示, 在平行四边形 中, 的平分线 交线段 于点 , 则 .
三、解答题(本大题共9题,共98分,解答应写出必要的文字说明、证明过程或演算步骤)
17.(1)计算:;
(2)解分式方程:.
18. 解不等式组请按下列步骤完成解答:
(1)解不等式①,得 ;
(2)解不等式②,得 ;
(3)将不等式①和②的解集在数轴上表示出来;
(4)原不等式组的解集为 .
19.先化简,再求值:
,从-1,2,3中选择一个适当的数作为x值代入.
20.如图,已知AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为2,∠ACD=30°,求图中阴影部分的面积.
21.已知:在平面直角坐标系中,的三个顶点的坐标分别为,,.
(1)画出关于原点成中心对称的,并写出点的坐标;
(2)画出将绕点按顺时针旋转所得的.
22.如图,在中,,D,E分别是,的中点,,.
(1)求证:四边形是菱形;
(2)连接交于点M,连接,若,,求,的长.
23. 如图,在中,过中点的直线分别交,的延长线于点,.
(1)求证:;
(2)连结,若,,的周长为16,求的周长.
24.如图,一次函数的图象与反比例函数的图象交于点,.
(1)求反比例函数和一次函数的解析式;
(2)利用图象,直接写出不等式的解集为 ;
(3)在轴上找一点,使△的周长最小,并求出最小值.
25.综合与实践
特例感知:
如图,在等边三角形中,是延长线上一点,且,以为边作等边三角形,连接,分别过点作,过点作,交于点,连接,与交于点.
(1)试判断和的数量关系,并说明理由.
(2)猜想论证:
将绕点按顺时针方向旋转一定角度得到图,则中和的数量关系是否仍然成立?请说明理由.
(3)拓展延伸:
将如图所示的绕点按逆时针方向旋转角度,当时,请直接写出的值.
参考答案
1.B
2.C
3.B
4.D
5.C
6.A
7.C
8.C
9.A
10.D
11.A
12.C
13.
14.
15.105°
16.2
17.(1)解:原式
;
(2)解:方程两边同时乘x2-4,得,
解得:,
经检验,不是原分式方程的解,
原分式方程无解.
18.(1)
(2)
(3)
(4)
19.解:
=,
∵当x+2≠0且x﹣2≠0,即x≠﹣2且x≠2时分式有意义,
∴取x=3,
当x=3时,原式==4.
20.(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠DAC=∠BAC,
∴∠DAC=∠OCA,
∴AD∥OC,
∵AD⊥EF,
∴OC⊥EF,
则EF为圆O的切线;
(2)解:∵∠ACD=30°,∠ADC=90°,
∴∠CAD=∠OCA=60°,
∴△AOC为等边三角形,
∴AC=OC=OA=2,
在Rt△ACD中,∠ACD=30°,
∴AD=AC=1,根据勾股定理得:CD=,
∴S阴影=S△ACD-(S扇形AOC-S△AOC)=×1×-()=.
21.(1)解:如图所示,
∴即为所求,其中点的坐标为.
(2)解:如图所示,
∴即为所求
22.(1)证明:∵,,
∴四边形是平行四边形,
∵,
∴,
∵D,E分别是,的中点,
∴是的中位线,,
∴,
∴,
∴四边形是菱形;
(2)解:如图所示:
∵四边形是菱形,
∴,,
∴,
是的中位线,
∴,,
在中,,
在中,,
∴.
23.(1)证明:∵四边形ABCD是平行四边形,
∴AO=CO,AD=BC,AD∥BC,
∴∠OAF=∠OCE,∠F=∠E,
在和中,
,
∴,
∴AF=CE,
∴CE-BC=AF-AD,
∴BE=DF;
(2)解:如图,连接CF,
∵EF⊥AC,AO=CO,
∴EF垂直平分AC,
∴AF=CF,
∵,,
∴2+DC+AF=16,
∴2+DC+AD+DF=2+DC+AD+2=4+DC+AD=16,
∴DC+AD=12,
∴的周长为2(DC+AD)=2×12=24.
24.(1)解:反比例函数的图象经过,
,
解得,
反比例函数的解析式为;
在中,当时,,
,
一次函数的图象与反比例函数的图象交于点,,
,
解得,
一次函数解析式为
(2)
(3)解:如图所示,作点关于轴的对称点,连接,,,,则,
由轴对称的性质可得,
,,
,
△的周长,
当有最小值时,△的周长有最小值,
,
当有最小值时,△的周长有最小值,
,
当、、三点共线时,有最小值,即此时△的周长有最小值,最小值为,
,,
,
△的周长的最小值为;
设直线解析式为,
则,
,
直线解析式为,
在中,当时,,
;
综上所述,当点的坐标为时,△的周长有最小值,最小值为.
25.(1)解:,理由如下:
和都是等边三角形,
,,,
,
,
,
,
,
,,
四边形是平行四边形,
,
,
在和中,
,
∴,
;
(2)解:仍然成立,理由如下:
如图,延长,交于,
和都是等边三角形,
,,,
,
,
,
,
,
,,
四边形是平行四边形,
,
,
在和中,
,
∴,
;
(3)解:①当α<90°,如图,延长,交ED的延长线于,
和都是等边三角形,
∴∠ABC=∠CDE=60°,
∵∠ABF=90°,
,
,
,
∵∠CDE=∠R+∠DCR,
,
,
②如图,延长交于,
由上知:,,
∵∠CED=∠CWE+∠WCE,
,
,
,
综上所述:或.
同课章节目录
