1.4.2.1 空间中的距离问题-暑期自我训练(含解析)高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.4.2.1 空间中的距离问题-暑期自我训练(含解析)高二上学期数学人教A版(2019)选择性必修第一册 |

|
|
| 格式 | docx | ||
| 文件大小 | 216.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 00:00:00 | ||
图片预览



文档简介
高二上学期数学人教A版(2019)选择性必修第一册
1.4.2.1 空间中的距离问题
A级——基础过关练
1.已知平面α的一个法向量为n=(-1,-2,2),A(0,1,0)为α内一点,则点P(1,0,1)到平面α的距离为( )
A.4 B.3
C.2 D.1
2.已知直线l经过点A(2,3,1),且向量n=(1,0,-1)所在直线与l垂直,则点P(4,3,2)到l的距离为( )
A. B.
C. D.1
3.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离等于( )
A. B.
C. D.
4.已知直线l的方向向量为a=(-1,0,1),点A(1,2,-1)在l上,则点P(2,-1,2)到l的距离为( )
A. B.4
C. D.3
5.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,M为棱A1B1上的一点,且A1M=λ(0<λ<2),设N为ME的中点,则点N到平面D1EF的距离为( )
A.λ B.
C.λ D.
6.(多选)下列四个命题中,正确的命题有( )
A.若一向量p在基底{a,b,c}下的坐标为(1,-2,3),则向量p在基底{a+b,a-b,c}下的坐标为
B.若向量a=(2,-1,2),b=(-4,2,m)且a⊥b,则m=-5
C.已知AB为平面α的一条斜线段,点A(1,2,-1)在平面α上,n=(1,0,1)为平面α的法向量,则点B(2,1,1)到平面α的距离为
D.若两个不同平面α,β的法向量分别是u,v,且u=(1,2,-2),v=(-2,-4,4),则α∥β
7.在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的中点,则直线MN到平面ACD1的距离为________.
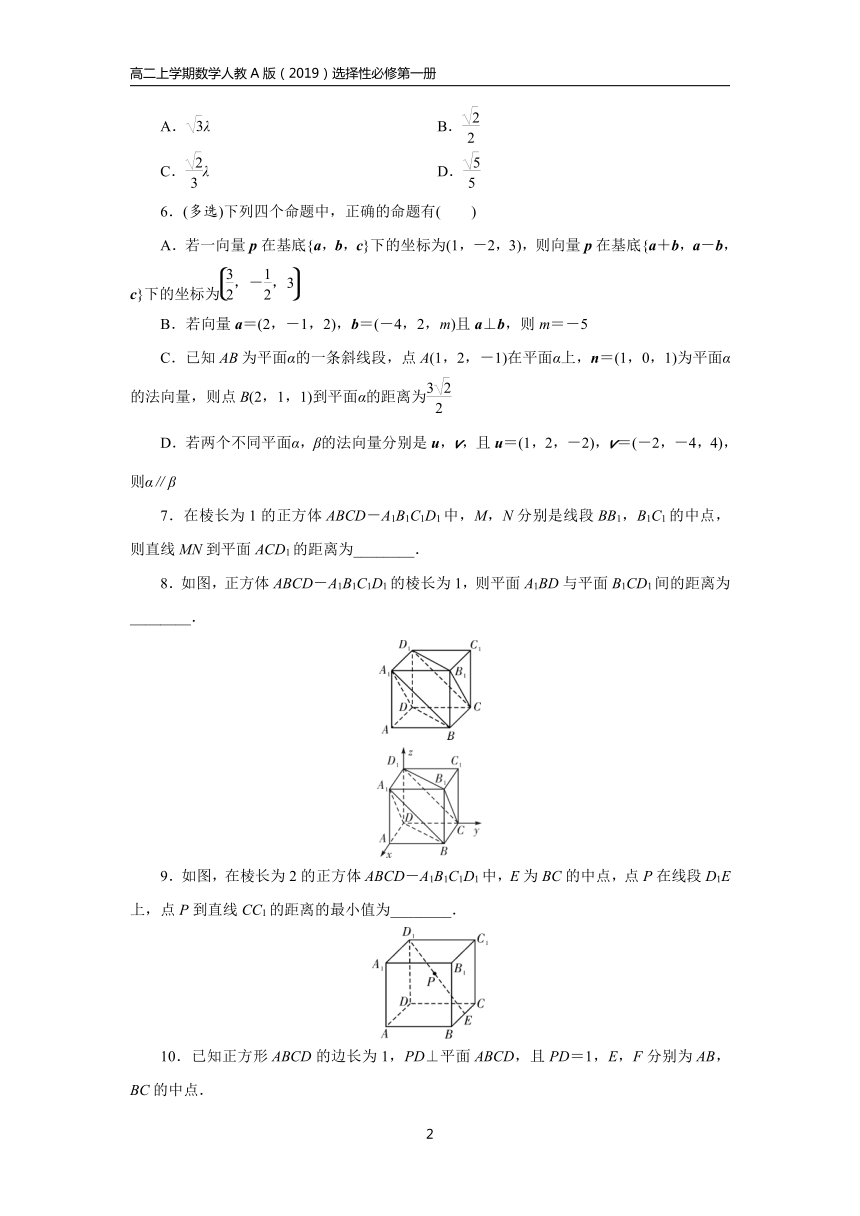
8.如图,正方体ABCD-A1B1C1D1的棱长为1,则平面A1BD与平面B1CD1间的距离为________.
9.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为________.
10.已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.
(1)求点P到直线EF的距离;
(2)求点D到平面PEF的距离;
(3)求直线AC到平面PEF的距离.
B级——综合运用练
11.(多选)如图,在四棱锥P-ABCD中,底面ABCD为矩形,AP⊥底面ABCD,AB=1,AD=3,AP=2,点E在PD上,=2,点M在棱PB上,则点M到平面ACE的距离可能为( )
A. B.
C. D.
12.如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,若AB=4,BC=2,CC1=3,BE=1,则||=________,点C到平面AEC1F的距离为________.
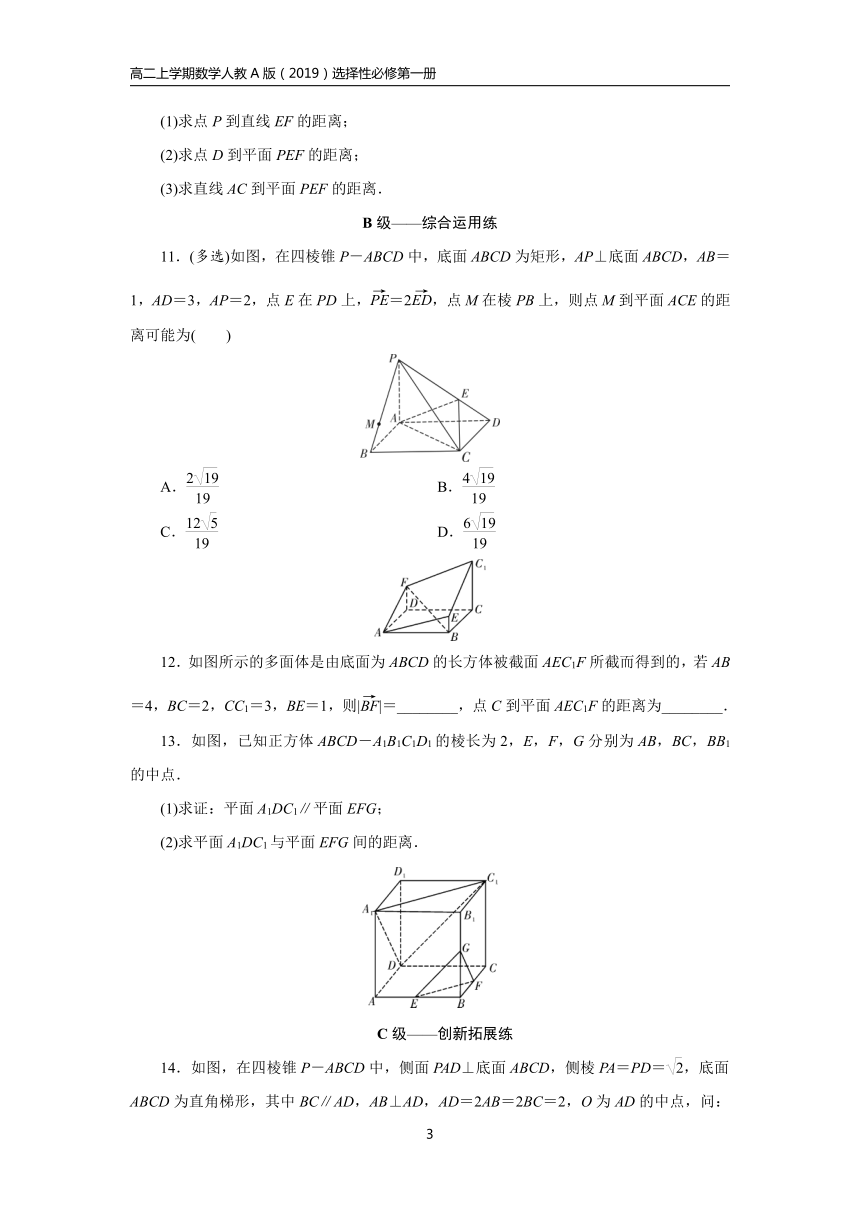
13.如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F,G分别为AB,BC,BB1的中点.
(1)求证:平面A1DC1∥平面EFG;
(2)求平面A1DC1与平面EFG间的距离.
C级——创新拓展练
14.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD的中点,问:线段AD上是否存在一点Q,使得它到平面PCD的距离为?若存在,求出的值;若不存在,说明理由.
参考答案
A级——基础过关练
1.【答案】D
【解析】因为=(1,-1,1),n=(-1,-2,2),所以·n=-1+2+2=3,|n|==3,则点P到平面α的距离d==1.故选D.
2.【答案】B
【解析】因为=(-2,0,-1),n与l垂直,所以点P到l的距离d===.故选B.
3.【答案】D
【解析】以D1为坐标原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(图略),则B1(2,2,0),C1(0,2,0),E(2,1,2),F(1,2,2),=(0,-1,2),=(-1,0,2).设平面B1EF的法向量为n=(x,y,z),则即令z=1,得n=(2,2,1).又因为=(-2,0,0),所以点C1到平面B1EF的距离h==.故选D.
4.【答案】C
【解析】因为A(1,2,-1),P(2,-1,2),所以=(-1,3,-3),则||=,|·|=,由点到直线的距离公式得d==.故选C.
5.【答案】D
【解析】以D为坐标原点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立空间直角坐标系(图略),则M(2,λ,2),D1(0,0,2),E(2,0,1),F(2,2,1),=(-2,0,1),=(0,2,0),=(0,λ,1).设平面D1EF的法向量为n=(x,y,z),则取x=1,得n=(1,0,2),所以点M到平面D1EF的距离d===.因为N为EM的中点,所以点N到平面D1EF的距离为.故选D.
6.【答案】CD
【解析】对于A,因为向量p在基底{a,b,c}下的坐标为(1,-2,3),则p=a-2b+3c,设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则p=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,所以解得x=-,y=,z=3,所以向量p在基底{a+b,a-b,c}下的坐标为,故A不正确;对于B,因为向量a=(2,-1,2),b=(-4,2,m),且a⊥b,所以a·b=-8-2+2m=0,解得m=5,故B不正确;对于C,=(1,-1,2),点B到平面α的距离d===,故C正确;对于D,两个不同平面α,β的法向量分别是u,v,且u=(1,2,-2),v=(-2,-4,4),因为v=-2u,所以v∥u,则α∥β,故D正确.故选CD.
7.【答案】
【解析】如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则D(0,0,0),C(0,1,0),D1(0,0,1),M,A(1,0,0).所以=,=(-1,1,0),AD1=(-1,0,1).设平面ACD1的法向量为n=(x,y,z),则即令x=1,则y=z=1,所以n=(1,1,1).所以点M到平面ACD1的距离d==.
8.【答案】
【解析】以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则D(0,0,0),A1(1,0,1),B(1,1,0),D1(0,0,1),则=(0,1,-1),=(-1,0,-1),=(-1,0,0).设平面A1BD的法向量为n=(x,y,z),则所以令z=1,得y=1,x=-1,所以n=(-1,1,1).所以点D1到平面A1BD的距离d===.因为平面A1BD与平面B1CD1间的距离等于点D1到平面A1BD的距离,所以平面A1BD与平面B1CD1间的距离为.
9.【答案】
【解析】如图,建立空间直角坐标系,则D1(0,0,2),E(1,2,0),=(-1,-2,2).
设P(x,y,z),=λ,λ∈[0,1],则=(x-1,y-2,z).所以(x-1,y-2,z)=λ(-1,-2,2),解得x=1-λ,y=2-2λ,z=2λ.所以P(1-λ,2-2λ,2λ).设点P在直线CC1上的射影为Q,得Q(0,2,2λ),||==,当λ=时,||min=.
10.解:建立如图所示的空间直角坐标系,则D(0,0,0),P(0,0,1),A(1,0,0),C(0,1,0),E,F.
(1)∵=,
取a==,u==×=,
则a2=,a·u=.
∴点P到直线EF的距离为==.
(2)∵=,=,=,设平面PEF的法向量为n=(x,y,z),
则解得
令x=2,则n=(2,2,3),
∴点D到平面PEF的距离d===.
(3)∵AC∥EF,∴直线AC到平面PEF的距离即点A到平面PEF的距离.
∵=,
∴点A到平面PEF的距离d===.
∴直线AC到平面PEF的距离为.
B级——综合运用练
11.【答案】BD
【解析】如图,以A为原点,,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系Axyz,
则A(0,0,0),P(0,0,2),B(1,0,0),C(1,3,0),E,所以=(1,3,0),=,=(-1,0,2).设平面ACE的法向量为n=(x,y,z),
由得令x=3,得n=(3,-1,3).设=λ(0≤λ≤1),则=+λ=(1-λ,0,2λ),所以点M到平面ACE的距离d==(λ+1).因为0≤λ≤1,所以≤d≤.故选BD.
12.【答案】2
【解析】如图,以D为原点,DA,DC,DF所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,a),由=,得(-2,0,a)=(-2,0,2),∴a=2,∴F(0,0,2),=(-2,-4,2),∴||=2.=(0,4,1),=(-2,0,2),设n=(x,y,z)为平面AEC1F的法向量,由得取z=1,则n=,∵=(0,0,3),∴点C到平面AEC1F的距离d==.
13.解:(1)∵E是AB的中点,F是BC的中点,
∴连接AC,得EF∥AC.
∵AA1∥CC1,∴ACC1A1是平行四边形.
∴A1C1∥AC.∴EF∥A1C1.
又∵A1C1 平面A1C1D,EF 平面A1C1D,
∴EF∥平面A1C1D.
同理,连接AB1,可得EG∥AB1∥DC1,可得EG∥平面A1C1D.
∵EF∩EG=E,EF,EG 平面EFG,
∴平面A1C1D∥平面EFG﹒
(2)如图,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Dxyz,则A1(2,0,2),C1(0,2,2),E(2,1,0),
∴=(2,0,2),1=(0,2,2),=(0,1,-2).
设平面A1DC1的法向量为n=(x,y,z),
则即取n=(1,1,-1),
则平面A1DC1与平面EFG间的距离为==﹒
C级——创新拓展练
14.解:存在.在△PAD中,PA=PD,O为AD的中点,所以PO⊥AD.
又因为侧面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PO⊥平面ABCD.
建立如图所示的空间直角坐标系,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),P(0,0,1),所以=(-1,0,1),=(-1,1,0).
假设存在点Q,使它到平面PCD的距离为.
设Q(0,y,0)(-1≤y≤1),则=(-1,y,0).
设平面PCD的法向量为n=(x0,y0,z0),则
所以即x0=y0=z0,
取x0=1,则平面PCD的一个法向量为n=(1,1,1).
所以点Q到平面PCD的距离d===,
所以y=-或y=(舍去).
此时AQ=,QD=.
所以存在点Q满足题意,此时=.
1.4.2.1 空间中的距离问题
A级——基础过关练
1.已知平面α的一个法向量为n=(-1,-2,2),A(0,1,0)为α内一点,则点P(1,0,1)到平面α的距离为( )
A.4 B.3
C.2 D.1
2.已知直线l经过点A(2,3,1),且向量n=(1,0,-1)所在直线与l垂直,则点P(4,3,2)到l的距离为( )
A. B.
C. D.1
3.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别是棱AB,BC的中点,则点C1到平面B1EF的距离等于( )
A. B.
C. D.
4.已知直线l的方向向量为a=(-1,0,1),点A(1,2,-1)在l上,则点P(2,-1,2)到l的距离为( )
A. B.4
C. D.3
5.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,BB1的中点,M为棱A1B1上的一点,且A1M=λ(0<λ<2),设N为ME的中点,则点N到平面D1EF的距离为( )
A.λ B.
C.λ D.
6.(多选)下列四个命题中,正确的命题有( )
A.若一向量p在基底{a,b,c}下的坐标为(1,-2,3),则向量p在基底{a+b,a-b,c}下的坐标为
B.若向量a=(2,-1,2),b=(-4,2,m)且a⊥b,则m=-5
C.已知AB为平面α的一条斜线段,点A(1,2,-1)在平面α上,n=(1,0,1)为平面α的法向量,则点B(2,1,1)到平面α的距离为
D.若两个不同平面α,β的法向量分别是u,v,且u=(1,2,-2),v=(-2,-4,4),则α∥β
7.在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是线段BB1,B1C1的中点,则直线MN到平面ACD1的距离为________.
8.如图,正方体ABCD-A1B1C1D1的棱长为1,则平面A1BD与平面B1CD1间的距离为________.
9.如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,点P到直线CC1的距离的最小值为________.
10.已知正方形ABCD的边长为1,PD⊥平面ABCD,且PD=1,E,F分别为AB,BC的中点.
(1)求点P到直线EF的距离;
(2)求点D到平面PEF的距离;
(3)求直线AC到平面PEF的距离.
B级——综合运用练
11.(多选)如图,在四棱锥P-ABCD中,底面ABCD为矩形,AP⊥底面ABCD,AB=1,AD=3,AP=2,点E在PD上,=2,点M在棱PB上,则点M到平面ACE的距离可能为( )
A. B.
C. D.
12.如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,若AB=4,BC=2,CC1=3,BE=1,则||=________,点C到平面AEC1F的距离为________.
13.如图,已知正方体ABCD-A1B1C1D1的棱长为2,E,F,G分别为AB,BC,BB1的中点.
(1)求证:平面A1DC1∥平面EFG;
(2)求平面A1DC1与平面EFG间的距离.
C级——创新拓展练
14.如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD的中点,问:线段AD上是否存在一点Q,使得它到平面PCD的距离为?若存在,求出的值;若不存在,说明理由.
参考答案
A级——基础过关练
1.【答案】D
【解析】因为=(1,-1,1),n=(-1,-2,2),所以·n=-1+2+2=3,|n|==3,则点P到平面α的距离d==1.故选D.
2.【答案】B
【解析】因为=(-2,0,-1),n与l垂直,所以点P到l的距离d===.故选B.
3.【答案】D
【解析】以D1为坐标原点,,,的方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(图略),则B1(2,2,0),C1(0,2,0),E(2,1,2),F(1,2,2),=(0,-1,2),=(-1,0,2).设平面B1EF的法向量为n=(x,y,z),则即令z=1,得n=(2,2,1).又因为=(-2,0,0),所以点C1到平面B1EF的距离h==.故选D.
4.【答案】C
【解析】因为A(1,2,-1),P(2,-1,2),所以=(-1,3,-3),则||=,|·|=,由点到直线的距离公式得d==.故选C.
5.【答案】D
【解析】以D为坐标原点,DA所在直线为x轴,DC所在直线为y轴,DD1所在直线为z轴,建立空间直角坐标系(图略),则M(2,λ,2),D1(0,0,2),E(2,0,1),F(2,2,1),=(-2,0,1),=(0,2,0),=(0,λ,1).设平面D1EF的法向量为n=(x,y,z),则取x=1,得n=(1,0,2),所以点M到平面D1EF的距离d===.因为N为EM的中点,所以点N到平面D1EF的距离为.故选D.
6.【答案】CD
【解析】对于A,因为向量p在基底{a,b,c}下的坐标为(1,-2,3),则p=a-2b+3c,设向量p在基底{a+b,a-b,c}下的坐标为(x,y,z),则p=x(a+b)+y(a-b)+zc=(x+y)a+(x-y)b+zc,所以解得x=-,y=,z=3,所以向量p在基底{a+b,a-b,c}下的坐标为,故A不正确;对于B,因为向量a=(2,-1,2),b=(-4,2,m),且a⊥b,所以a·b=-8-2+2m=0,解得m=5,故B不正确;对于C,=(1,-1,2),点B到平面α的距离d===,故C正确;对于D,两个不同平面α,β的法向量分别是u,v,且u=(1,2,-2),v=(-2,-4,4),因为v=-2u,所以v∥u,则α∥β,故D正确.故选CD.
7.【答案】
【解析】如图,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则D(0,0,0),C(0,1,0),D1(0,0,1),M,A(1,0,0).所以=,=(-1,1,0),AD1=(-1,0,1).设平面ACD1的法向量为n=(x,y,z),则即令x=1,则y=z=1,所以n=(1,1,1).所以点M到平面ACD1的距离d==.
8.【答案】
【解析】以D为坐标原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立如图所示的空间直角坐标系,则D(0,0,0),A1(1,0,1),B(1,1,0),D1(0,0,1),则=(0,1,-1),=(-1,0,-1),=(-1,0,0).设平面A1BD的法向量为n=(x,y,z),则所以令z=1,得y=1,x=-1,所以n=(-1,1,1).所以点D1到平面A1BD的距离d===.因为平面A1BD与平面B1CD1间的距离等于点D1到平面A1BD的距离,所以平面A1BD与平面B1CD1间的距离为.
9.【答案】
【解析】如图,建立空间直角坐标系,则D1(0,0,2),E(1,2,0),=(-1,-2,2).
设P(x,y,z),=λ,λ∈[0,1],则=(x-1,y-2,z).所以(x-1,y-2,z)=λ(-1,-2,2),解得x=1-λ,y=2-2λ,z=2λ.所以P(1-λ,2-2λ,2λ).设点P在直线CC1上的射影为Q,得Q(0,2,2λ),||==,当λ=时,||min=.
10.解:建立如图所示的空间直角坐标系,则D(0,0,0),P(0,0,1),A(1,0,0),C(0,1,0),E,F.
(1)∵=,
取a==,u==×=,
则a2=,a·u=.
∴点P到直线EF的距离为==.
(2)∵=,=,=,设平面PEF的法向量为n=(x,y,z),
则解得
令x=2,则n=(2,2,3),
∴点D到平面PEF的距离d===.
(3)∵AC∥EF,∴直线AC到平面PEF的距离即点A到平面PEF的距离.
∵=,
∴点A到平面PEF的距离d===.
∴直线AC到平面PEF的距离为.
B级——综合运用练
11.【答案】BD
【解析】如图,以A为原点,,,的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系Axyz,
则A(0,0,0),P(0,0,2),B(1,0,0),C(1,3,0),E,所以=(1,3,0),=,=(-1,0,2).设平面ACE的法向量为n=(x,y,z),
由得令x=3,得n=(3,-1,3).设=λ(0≤λ≤1),则=+λ=(1-λ,0,2λ),所以点M到平面ACE的距离d==(λ+1).因为0≤λ≤1,所以≤d≤.故选BD.
12.【答案】2
【解析】如图,以D为原点,DA,DC,DF所在直线分别为x轴、y轴、z轴建立空间直角坐标系,则D(0,0,0),B(2,4,0),A(2,0,0),C(0,4,0),E(2,4,1),C1(0,4,3).设F(0,0,a),由=,得(-2,0,a)=(-2,0,2),∴a=2,∴F(0,0,2),=(-2,-4,2),∴||=2.=(0,4,1),=(-2,0,2),设n=(x,y,z)为平面AEC1F的法向量,由得取z=1,则n=,∵=(0,0,3),∴点C到平面AEC1F的距离d==.
13.解:(1)∵E是AB的中点,F是BC的中点,
∴连接AC,得EF∥AC.
∵AA1∥CC1,∴ACC1A1是平行四边形.
∴A1C1∥AC.∴EF∥A1C1.
又∵A1C1 平面A1C1D,EF 平面A1C1D,
∴EF∥平面A1C1D.
同理,连接AB1,可得EG∥AB1∥DC1,可得EG∥平面A1C1D.
∵EF∩EG=E,EF,EG 平面EFG,
∴平面A1C1D∥平面EFG﹒
(2)如图,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Dxyz,则A1(2,0,2),C1(0,2,2),E(2,1,0),
∴=(2,0,2),1=(0,2,2),=(0,1,-2).
设平面A1DC1的法向量为n=(x,y,z),
则即取n=(1,1,-1),
则平面A1DC1与平面EFG间的距离为==﹒
C级——创新拓展练
14.解:存在.在△PAD中,PA=PD,O为AD的中点,所以PO⊥AD.
又因为侧面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
所以PO⊥平面ABCD.
建立如图所示的空间直角坐标系,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),P(0,0,1),所以=(-1,0,1),=(-1,1,0).
假设存在点Q,使它到平面PCD的距离为.
设Q(0,y,0)(-1≤y≤1),则=(-1,y,0).
设平面PCD的法向量为n=(x0,y0,z0),则
所以即x0=y0=z0,
取x0=1,则平面PCD的一个法向量为n=(1,1,1).
所以点Q到平面PCD的距离d===,
所以y=-或y=(舍去).
此时AQ=,QD=.
所以存在点Q满足题意,此时=.
