1.8.1 有理数的乘法 课件 (共26张PPT) 冀教版(2024)数学七年级上册
文档属性
| 名称 | 1.8.1 有理数的乘法 课件 (共26张PPT) 冀教版(2024)数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 14.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-30 16:07:47 | ||
图片预览








文档简介
(共26张PPT)
[图片]
冀教版(2024)
七年级上册
1.8.1 有理数的乘法
学习目标
理解有理数乘法法则,会用法则进行乘法运算.(重点)
01
能借助有理数乘法掌握倒数的概念,准确找出非零有理数的倒数.(重点)
02
运用有理数的乘法,解决实际问题.(难点)
03
我们学过的乘法,乘数都是正数或0. 在有理数范围内,如何进行乘法运算呢?
新课导学
有理数乘法法则:
两数相乘,同号为正,异号得负,并把绝对值相乘;
任何数与0相乘,都得0.
新知探索
通过测量某学校实验楼的楼梯得知,每级台阶的高都是15cm. 现在规定:一楼大厅地面的高度为0cm,从一楼大厅往楼上方向为正方向,从一楼大厅往地下室方向为负方向.
小亮从一楼大厅向楼上走1,2,3,4级台阶时,他所在的高度分别为
15 1 15 (cm); 15 2 30 (cm);
15 3 45 (cm); 15 4 60 (cm).
新知探索
1.请在下面的横线上分别填写大华从一楼大厅向地下室走1,2,3,4级台阶时,他所在的高度:
(15) 1 _____ (cm); (15) 2 _____(cm);
(15) 3 _____ (cm); (15) 4 _____ (cm).
2.比较上面的两组算式,你认为当两数相乘时,如果把一个因数换成它的相反数,那么它们的乘积有什么关系?
解:当两数相乘时,把一个因数换成它的相反数,乘积也变为原来的相反数.
15
60
45
30
新知探索
3.根据你的判断,写出以下各式的结果.
(15) (1) ____(cm);
(15) (2) ____(cm);
(15) (3) ____(cm);
(15) (4) ____(cm).
15
45
30
60
新知探索
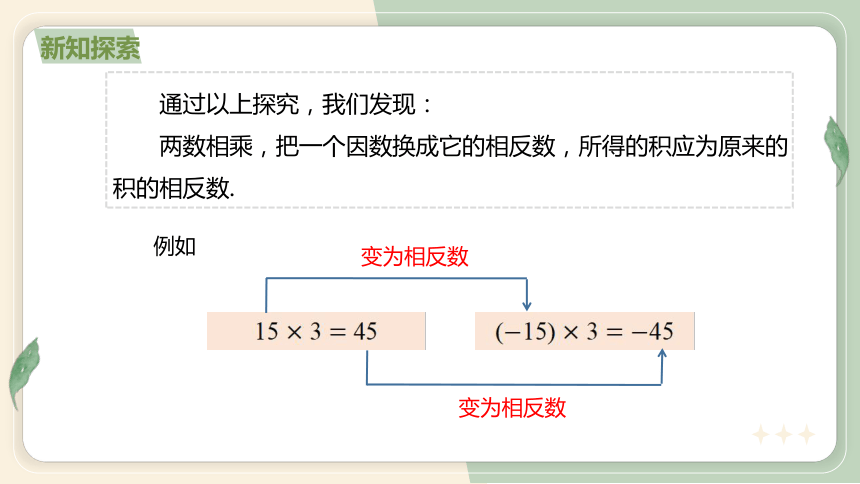
通过以上探究,我们发现:
两数相乘,把一个因数换成它的相反数,所得的积应为原来的积的相反数.
例如
15 3 45
(15) 3 45
变为相反数
变为相反数
有理数乘法法则
新知探索
两数相乘,同号得正,异号得负,并把这两数的绝对值相乘.
任何数同 0 相乘,仍得 0.
新知探索
新知探索
倒数
新知探索
如果两个有理数的乘积是1,那么我们称其中一个数为另一个数的倒数,也称这两个有理数互为倒数.
例如,是6的倒数,和6互为倒数;2是 的倒数,2和 互为倒数. 0没有倒数.
显然,一个正数的倒数是正数,一个负数的倒数是负数.
新知探索
例2 通常情况下,海拔每增加1km,气温就降低大约6°C(气温降低记为负). 某校七年级科技兴趣小组在海拔为1000m 的山腰上测得气温为12°C. 请推算此山海拔为3500m处的气温大约是多少摄氏度.
新知探索
解:1000m 1km,3500m 3.5km.
12 (6) (3.51)
= 12 (15)
= 12 15
= 3(℃).
答:此山海拔为3500m处的气温大约是零下 3℃.
练习
解:(1)正;(2)负;
(3)负; (4)正.
练习
练习
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
6
新知探索
1、有理数的乘法法则.
2、倒数的概念.
课堂总结
谢谢观看
[图片]
冀教版(2024)
七年级上册
1.8.1 有理数的乘法
学习目标
理解有理数乘法法则,会用法则进行乘法运算.(重点)
01
能借助有理数乘法掌握倒数的概念,准确找出非零有理数的倒数.(重点)
02
运用有理数的乘法,解决实际问题.(难点)
03
我们学过的乘法,乘数都是正数或0. 在有理数范围内,如何进行乘法运算呢?
新课导学
有理数乘法法则:
两数相乘,同号为正,异号得负,并把绝对值相乘;
任何数与0相乘,都得0.
新知探索
通过测量某学校实验楼的楼梯得知,每级台阶的高都是15cm. 现在规定:一楼大厅地面的高度为0cm,从一楼大厅往楼上方向为正方向,从一楼大厅往地下室方向为负方向.
小亮从一楼大厅向楼上走1,2,3,4级台阶时,他所在的高度分别为
15 1 15 (cm); 15 2 30 (cm);
15 3 45 (cm); 15 4 60 (cm).
新知探索
1.请在下面的横线上分别填写大华从一楼大厅向地下室走1,2,3,4级台阶时,他所在的高度:
(15) 1 _____ (cm); (15) 2 _____(cm);
(15) 3 _____ (cm); (15) 4 _____ (cm).
2.比较上面的两组算式,你认为当两数相乘时,如果把一个因数换成它的相反数,那么它们的乘积有什么关系?
解:当两数相乘时,把一个因数换成它的相反数,乘积也变为原来的相反数.
15
60
45
30
新知探索
3.根据你的判断,写出以下各式的结果.
(15) (1) ____(cm);
(15) (2) ____(cm);
(15) (3) ____(cm);
(15) (4) ____(cm).
15
45
30
60
新知探索
通过以上探究,我们发现:
两数相乘,把一个因数换成它的相反数,所得的积应为原来的积的相反数.
例如
15 3 45
(15) 3 45
变为相反数
变为相反数
有理数乘法法则
新知探索
两数相乘,同号得正,异号得负,并把这两数的绝对值相乘.
任何数同 0 相乘,仍得 0.
新知探索
新知探索
倒数
新知探索
如果两个有理数的乘积是1,那么我们称其中一个数为另一个数的倒数,也称这两个有理数互为倒数.
例如,是6的倒数,和6互为倒数;2是 的倒数,2和 互为倒数. 0没有倒数.
显然,一个正数的倒数是正数,一个负数的倒数是负数.
新知探索
例2 通常情况下,海拔每增加1km,气温就降低大约6°C(气温降低记为负). 某校七年级科技兴趣小组在海拔为1000m 的山腰上测得气温为12°C. 请推算此山海拔为3500m处的气温大约是多少摄氏度.
新知探索
解:1000m 1km,3500m 3.5km.
12 (6) (3.51)
= 12 (15)
= 12 15
= 3(℃).
答:此山海拔为3500m处的气温大约是零下 3℃.
练习
解:(1)正;(2)负;
(3)负; (4)正.
练习
练习
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
6
新知探索
1、有理数的乘法法则.
2、倒数的概念.
课堂总结
谢谢观看
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
