人教版2024—2025学年八年级下册数学期末考试模拟试卷(二)(含答案)
文档属性
| 名称 | 人教版2024—2025学年八年级下册数学期末考试模拟试卷(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1010.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 12:47:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年八年级下册数学期末考试模拟试卷(二)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.一组数据是:35,42,36,38,40,75,42,50,这组数据的中位数是( )
A.38 B.39 C.40 D.41
2.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
3.下列各组数中,能构成直角三角形的是( )
A. B. C.3,4,5 D.1,2,3
4.如图,在平行四边形中,,则的度数是( )
A. B. C. D.
5.如图,在菱形中,,,则菱形的面积为( )
A.8 B. C. D.
6.在平面直角坐标系中,函数的图象会经过第( )
A.一、二、三象限 B.一、二、四象限
C.一、三、四象限 D.二、三、四象限
7.如图,在中,,,.点E、F分别是边、上的点,连结,将沿翻折,使得点的对称点落在边的中点处,则的长为( )
A. B. C.3 D.2
8.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,连接,交于点P.如图所示,若,,则正方形的面积为( )
A.28 B.25 C.30 D.24
9.如图,在中,,,,为边上一动点,于,于,连接,则的最小值为( )
A.1.5 B.2 C.2.4 D.2.5
10.如图(),点为边的中点,点在上,动点以每秒的速度沿图()的边运动,运动路径为,相应的的面积()关于运动时间()的函数图象如图(),若,则下列结论正确的个数有( )
①图()中长;
②图()中的长是;
③图()中点表示4秒时的值为;
④图()中的点表示12秒时值为.
A. 个 B. 个 C. 个 D. 个
二、填空题(每小题3分,满分18分)
11.学校举行科技创新比赛,对创新设计和现场展示两个方面评分的权重分别设为来计算选手的综合成绩.小华本次比赛的两项成绩分别是:创新设计分,现场展示分,则他的综合成绩是 分.
12.裕固族工匠用银片制作饰品,其中有一个长方形银片的面积为,长为,则该长方形银片的宽为 .
13.如图,点在同侧,,则 .
14.如图,直线(为常数且)与直线(为常数)交于点,则关于的不等式的解集是 .
15.如图,在中,的平分线交于点E,交的延长线于点F,若,,则 .
16.如图,在中,,以的三条边为边在上方作正方形,正方形,正方形,且恰好经过点,、交于点,若,则的面积是 .
人教版2024—2025学年八年级下册数学期末考试模拟试卷(二)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);(2).
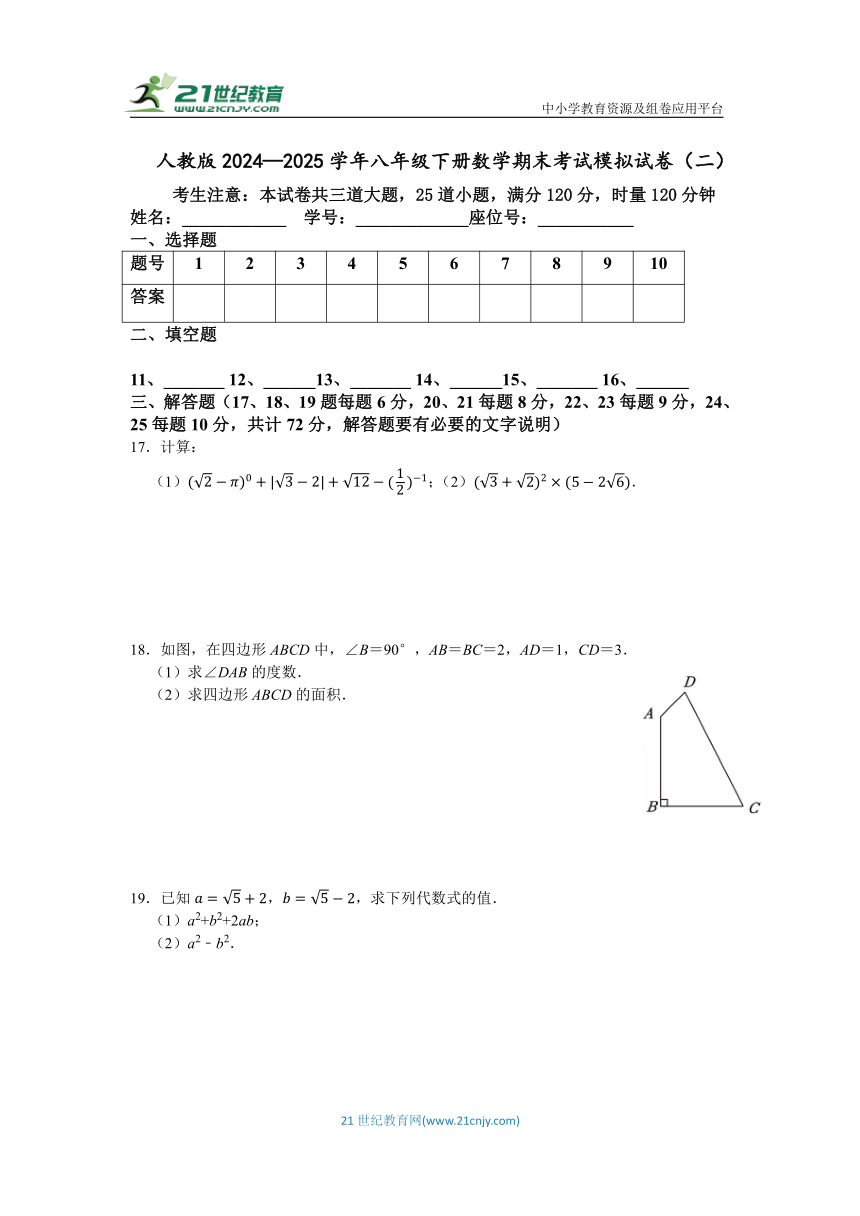
18.如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
19.已知,,求下列代数式的值.
(1)a2+b2+2ab;
(2)a2﹣b2.
20.在△ABC中,∠BAC=90°,AD=BD,过点A作AE∥BC,且AE=BD,连结CE.
(1)证明:四边形ADCE是菱形;
(2)连接DE交AC于点O,作AF⊥CD于F,若,,求线段AF的长.
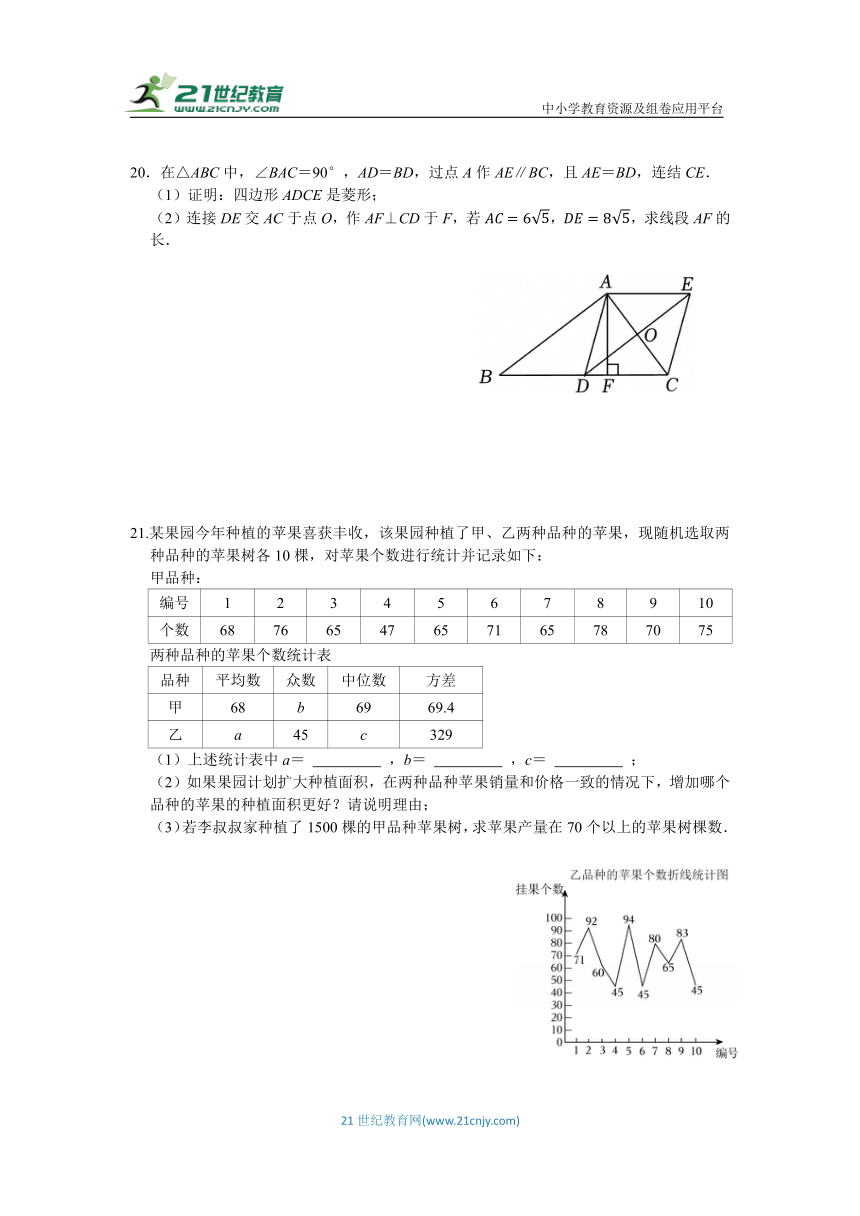
21.某果园今年种植的苹果喜获丰收,该果园种植了甲、乙两种品种的苹果,现随机选取两种品种的苹果树各10棵,对苹果个数进行统计并记录如下:
甲品种:
编号 1 2 3 4 5 6 7 8 9 10
个数 68 76 65 47 65 71 65 78 70 75
两种品种的苹果个数统计表
品种 平均数 众数 中位数 方差
甲 68 b 69 69.4
乙 a 45 c 329
(1)上述统计表中a= ,b= ,c= ;
(2)如果果园计划扩大种植面积,在两种品种苹果销量和价格一致的情况下,增加哪个品种的苹果的种植面积更好?请说明理由;
(3)若李叔叔家种植了1500棵的甲品种苹果树,求苹果产量在70个以上的苹果树棵数.
22.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,EF⊥AB于F点,OG∥EF交AB于点G.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BD的长.
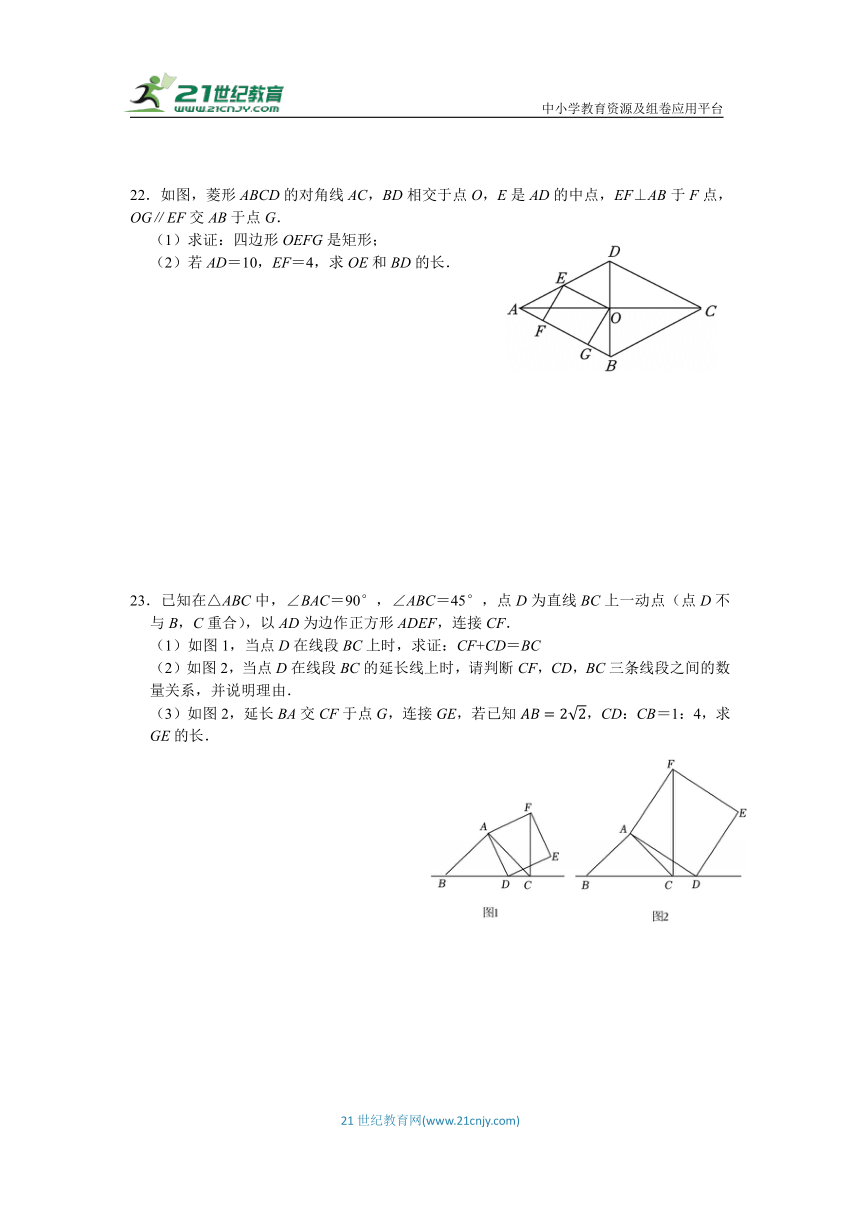
23.已知在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与B,C重合),以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:CF+CD=BC
(2)如图2,当点D在线段BC的延长线上时,请判断CF,CD,BC三条线段之间的数量关系,并说明理由.
(3)如图2,延长BA交CF于点G,连接GE,若已知,CD:CB=1:4,求GE的长.
24.在平面直角坐标系xOy中,点A(0,3),点B(m,0),以AB为腰作等腰Rt△ABC,如图所示.
(1)若S△ABC的值为5平方单位,求m的值;
(2)BC交y轴于点D,CE⊥y轴于点E,当y轴平分∠BAC时,求的值;
(3)连接OC,当OC+AC最小时,求点C的坐标.
25.如图,O为原点,四边形OABC为矩形,已知A(10,0),C(0,3),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当t= 时,四边形PODB是平行四边形;
(2)在线段BC上是否存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)在线段PB上有一点M,且PM=5,求四边形OAMP周长的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D D C A A C D
二、填空题
11.【解】解:由题意得:他的综合成绩是分(分),
故答案为:.
12.【解】解:∵长方形银片的面积为,长为,
∴该长方形银片的宽为,
故选:.
13.【解】解:过点作垂线交于点,即
,即是的垂直平分线,
∵,
在同一线上,
,
故答案为:.
14.【解】解:∵直线与直线交于点,
∴根据图象可知,当时,直线的图象在线的下面,
∴关于x的不等式的解集是.
故答案为:.
15.【解】解:∵平分,
∴,
∵,
∴
∴,,
∴,
∴,,
∵,,
∴,
∴,
故答案为:15.
16.【解】解:如图:
∵四边形是正方形,
∴,
∴,
∴
∴,
∵四边形是正方形,
∴,,
∵,
∴,
∴,
∴,
∴,
∵
,
,
∴,
∴,
∵,,
∴
∵
.
故答案为:.
三、解答题
17.【解答】解:(1)
;
(2)
=25﹣24
=1.
18.【解答】解:(1)连接AC,
∵∠B=90°,AB=BC=2,
∴,∠BAC=45°,
∵AD=1,CD=3,
∴,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=135°.
(2)在 Rt△ABC中,,
在 Rt△ADC中,.
∴.
19.【解答】解:(1)原式=(a+b)2
=20;
(2)原式=(a+b)(a﹣b)
.
20.【解答】(1)证明:∵AE∥BC,AE=BD,
∴四边形AEDB是平行四边形,
∴AB∥DE,
∵∠BAC=90°,AD=BD,
∴∠B=∠BAD,
∵∠B+∠ACB=∠BAD+∠CAD=90°,
∴∠ACD=∠CAD,
∴AD=CD,
∵AE=BD,
∴AE=CD,
∴四边形ADCE是平行四边形,
∵AD=CD,
∴四边形ADCE是菱形;
(2)解:∵四边形ADCE是菱形,,,
∴,,
在Rt△AOD中,,
∴,
即,
∴.
21.【解答】解:(1)乙品种的平均数为(71+92+60+45+94+45+80+65+83+45)÷10=68(个),
甲品种的众数为65,
乙品种的中位数为68;
故答案为:68,65,68;
(2)增加甲品种的苹果种植面积更好,
理由:甲品种平均产量和乙品种一致,但甲品种方差更小,稳定性更好,同时它的众数和中位数均高于乙品种,大面积种植风险更小,故选甲;
(3)1500600(棵),
答:苹果产量在70个以上的苹果树约有600棵.
22.【解答】(1)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=10,AC⊥BD,
∴∠AOD=90°,
∵E是AD的中点,
∴,
由(1)可知,四边形EFCO是矩形,
∴FG=OE=5,
∵EF⊥AB,
∴∠EFA=90°,
∴,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2,
∵在直角三角形OGB中OB2=BG2+OG2=22+42=20,
∴,
∴.
23.【解答】(1)证明:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∵BD+CD=BC,
∴CF+CD=BC;
(2)解:CF﹣CD=BC;理由如下:
∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴BC+CD=CF,
∴CF﹣CD=BC;
(3)解:如图2,过点A作AN⊥BC,过点E作EH⊥CF,
∵,
∴,
∵AN⊥BC,
∴BN=CN=2,
∵∠ABC=45°,AN⊥BC,
∴AN=BN=2,
∵BC:CD=4:1,
∴CD=1,
∴ND=3,
由(2)知:△ABD≌△ACF,
∴BD=CF=BC+CD=5,∠ACF=∠B=45°,∠AFC=∠ADB,
∴∠BCF=∠ACB+∠ACF=90°,
∵∠B=45°,
∴BC=CG=4,
∴FG=1,
∵∠AFC+∠EFC=∠AFE=90°,∠ADB+∠DAN=90°,∠AFC=∠ADB,
∴∠DAN=∠EFC,
在△AND和△FHE中,
,
∴△AND≌△FHE(AAS),
∴EH=DN=3,HF=AN=2,
∴GH=FH﹣FG=1,
在直角三角形EHG中,由勾股定理得:.
24.【解答】解:(1)∵△ABC是等腰直角三角形,
∴S△ABCAB2,
∴AB2=10,
∵AO2+BO2=AB2,
∴9+BO2=10,
∴BO=1,
∵点B在x轴的负半轴,
∴m=﹣1;
(2)如图2,延长CE,AB交于点H,
∵y轴平分∠BAC,
∴∠CAE=∠HAE,
在△AEH和△AEC中,
,
∴△AEH≌△AEC(ASA),
∴HE=EC,
∴CH=2EC,
∵∠H+∠HAE=90°,∠H+∠HCB=90°,
∴∠HAE=∠HCE,
又∵AB=BC,∠ABC=∠CBH=90°,
∴△ABD≌△CBH(ASA),
∴AD=CH=2CE,
∴2;
(3)如图3,过点C作CP⊥x轴于P,
∵∠ABO+∠CBP=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠CBP,
又∵∠AOB=∠BPC=90°,AB=BC,
∴△ABO≌△BCP(AAS),
∴BO=CP=﹣m,AO=BP=3,
∴OP=m+3,
∴点C坐标为(m+3,m),
∴点C在直线y=x﹣3上运动,
如图,直线y=x﹣3与x轴交于点K,与y轴交于点M,过点O作MK的对称点N,连接ON交直线MK于点F,连接AN交MK于点C',即点C'为所求点,
∴点M(0,﹣3),点N(3,0),
∴OM=OK,
∵点O,点N关于直线MK对称,
∴OF⊥MK,OF=FN,
∴点F(,),
∴点N(3,﹣3),
∴直线AN解析式为:y=﹣2x+3,
联立方程组,
解得,
∴点C坐标为(2,﹣1).
25.【解答】解:(1)∵四边形OABC为矩形,A(10,0),C(0,3),动点P在线段BC上以每秒2个单位长的速度由点C向B运动,点P的运动时间为t,
∴CB=OA=10,AB=OC=3,∠B=∠OAB=∠OCB=90°,CB∥OA,
∵点D是OA的中点,
∴,
由题意得:CP=2t,
∴PB=CB﹣CP=10﹣2t,
∵四边形PODB是平行四边形,
∴PB=OD=5,
∴10﹣2t=5,
∴t=2.5,
故答案为:2.5;
(2)在线段BC上存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形;理由如下:
分两种情况讨论:
①如图,当Q点在P的右边时,
∵四边形ODQP为菱形,
∴OP=PQ=OD=5,
在Rt△OPC中,由勾股定理得:,
∴2t=4,
∴t=2,
∵CQ=CP+PQ=4+5=9,
∴Q(9,3);
②如图2,当Q点在P的左边时,
∵四边形ODQP为菱形,
∴OQ=PQ=OD=5,
在Rt△OCQ中,,
∴CP=CQ+PQ=4+5=9,
∴2t=9,
∴t=4.5,
∵CQ=4,
∴Q(4,3);
综上所述,t=2秒时,Q(9,3);t=4.5秒时,Q(4,3);
(3)如图3,由(1)知:OD=5,
∵PM=5,
∴OD=PM,
∵CB∥OA,
∴四边形OPMD是平行四边形,
∴OP=DM,
∵四边形OAMP的周长为:
OA+AM+PM+OP
=10+AM+5+DM
=15+AM+DM,
∴AM+DM最小时,四边形OAMP的周长最小,
∴作点A关于BC的对称点E,连接DE交PB于M,
∴AM=EM,
∴AM+DM=DM+EM,
∵两点之间线段最短,
∴此时DM+EM最小,即AM+DM最小,
∵AE=AB+BE=3+3=6,
∴AM+DM的最小值为:,
∴四边形OAMP的周长最小值为.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年八年级下册数学期末考试模拟试卷(二)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.一组数据是:35,42,36,38,40,75,42,50,这组数据的中位数是( )
A.38 B.39 C.40 D.41
2.下列二次根式中,属于最简二次根式的是( )
A. B. C. D.
3.下列各组数中,能构成直角三角形的是( )
A. B. C.3,4,5 D.1,2,3
4.如图,在平行四边形中,,则的度数是( )
A. B. C. D.
5.如图,在菱形中,,,则菱形的面积为( )
A.8 B. C. D.
6.在平面直角坐标系中,函数的图象会经过第( )
A.一、二、三象限 B.一、二、四象限
C.一、三、四象限 D.二、三、四象限
7.如图,在中,,,.点E、F分别是边、上的点,连结,将沿翻折,使得点的对称点落在边的中点处,则的长为( )
A. B. C.3 D.2
8.我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,连接,交于点P.如图所示,若,,则正方形的面积为( )
A.28 B.25 C.30 D.24
9.如图,在中,,,,为边上一动点,于,于,连接,则的最小值为( )
A.1.5 B.2 C.2.4 D.2.5
10.如图(),点为边的中点,点在上,动点以每秒的速度沿图()的边运动,运动路径为,相应的的面积()关于运动时间()的函数图象如图(),若,则下列结论正确的个数有( )
①图()中长;
②图()中的长是;
③图()中点表示4秒时的值为;
④图()中的点表示12秒时值为.
A. 个 B. 个 C. 个 D. 个
二、填空题(每小题3分,满分18分)
11.学校举行科技创新比赛,对创新设计和现场展示两个方面评分的权重分别设为来计算选手的综合成绩.小华本次比赛的两项成绩分别是:创新设计分,现场展示分,则他的综合成绩是 分.
12.裕固族工匠用银片制作饰品,其中有一个长方形银片的面积为,长为,则该长方形银片的宽为 .
13.如图,点在同侧,,则 .
14.如图,直线(为常数且)与直线(为常数)交于点,则关于的不等式的解集是 .
15.如图,在中,的平分线交于点E,交的延长线于点F,若,,则 .
16.如图,在中,,以的三条边为边在上方作正方形,正方形,正方形,且恰好经过点,、交于点,若,则的面积是 .
人教版2024—2025学年八年级下册数学期末考试模拟试卷(二)
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1);(2).
18.如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.
(1)求∠DAB的度数.
(2)求四边形ABCD的面积.
19.已知,,求下列代数式的值.
(1)a2+b2+2ab;
(2)a2﹣b2.
20.在△ABC中,∠BAC=90°,AD=BD,过点A作AE∥BC,且AE=BD,连结CE.
(1)证明:四边形ADCE是菱形;
(2)连接DE交AC于点O,作AF⊥CD于F,若,,求线段AF的长.
21.某果园今年种植的苹果喜获丰收,该果园种植了甲、乙两种品种的苹果,现随机选取两种品种的苹果树各10棵,对苹果个数进行统计并记录如下:
甲品种:
编号 1 2 3 4 5 6 7 8 9 10
个数 68 76 65 47 65 71 65 78 70 75
两种品种的苹果个数统计表
品种 平均数 众数 中位数 方差
甲 68 b 69 69.4
乙 a 45 c 329
(1)上述统计表中a= ,b= ,c= ;
(2)如果果园计划扩大种植面积,在两种品种苹果销量和价格一致的情况下,增加哪个品种的苹果的种植面积更好?请说明理由;
(3)若李叔叔家种植了1500棵的甲品种苹果树,求苹果产量在70个以上的苹果树棵数.
22.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,EF⊥AB于F点,OG∥EF交AB于点G.
(1)求证:四边形OEFG是矩形;
(2)若AD=10,EF=4,求OE和BD的长.
23.已知在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与B,C重合),以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:CF+CD=BC
(2)如图2,当点D在线段BC的延长线上时,请判断CF,CD,BC三条线段之间的数量关系,并说明理由.
(3)如图2,延长BA交CF于点G,连接GE,若已知,CD:CB=1:4,求GE的长.
24.在平面直角坐标系xOy中,点A(0,3),点B(m,0),以AB为腰作等腰Rt△ABC,如图所示.
(1)若S△ABC的值为5平方单位,求m的值;
(2)BC交y轴于点D,CE⊥y轴于点E,当y轴平分∠BAC时,求的值;
(3)连接OC,当OC+AC最小时,求点C的坐标.
25.如图,O为原点,四边形OABC为矩形,已知A(10,0),C(0,3),点D是OA的中点,动点P在线段BC上以每秒2个单位长的速度由点C向B运动.设动点P的运动时间为t秒.
(1)当t= 时,四边形PODB是平行四边形;
(2)在线段BC上是否存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(3)在线段PB上有一点M,且PM=5,求四边形OAMP周长的最小值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D D C A A C D
二、填空题
11.【解】解:由题意得:他的综合成绩是分(分),
故答案为:.
12.【解】解:∵长方形银片的面积为,长为,
∴该长方形银片的宽为,
故选:.
13.【解】解:过点作垂线交于点,即
,即是的垂直平分线,
∵,
在同一线上,
,
故答案为:.
14.【解】解:∵直线与直线交于点,
∴根据图象可知,当时,直线的图象在线的下面,
∴关于x的不等式的解集是.
故答案为:.
15.【解】解:∵平分,
∴,
∵,
∴
∴,,
∴,
∴,,
∵,,
∴,
∴,
故答案为:15.
16.【解】解:如图:
∵四边形是正方形,
∴,
∴,
∴
∴,
∵四边形是正方形,
∴,,
∵,
∴,
∴,
∴,
∴,
∵
,
,
∴,
∴,
∵,,
∴
∵
.
故答案为:.
三、解答题
17.【解答】解:(1)
;
(2)
=25﹣24
=1.
18.【解答】解:(1)连接AC,
∵∠B=90°,AB=BC=2,
∴,∠BAC=45°,
∵AD=1,CD=3,
∴,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
∴∠DAB=∠DAC+∠BAC=135°.
(2)在 Rt△ABC中,,
在 Rt△ADC中,.
∴.
19.【解答】解:(1)原式=(a+b)2
=20;
(2)原式=(a+b)(a﹣b)
.
20.【解答】(1)证明:∵AE∥BC,AE=BD,
∴四边形AEDB是平行四边形,
∴AB∥DE,
∵∠BAC=90°,AD=BD,
∴∠B=∠BAD,
∵∠B+∠ACB=∠BAD+∠CAD=90°,
∴∠ACD=∠CAD,
∴AD=CD,
∵AE=BD,
∴AE=CD,
∴四边形ADCE是平行四边形,
∵AD=CD,
∴四边形ADCE是菱形;
(2)解:∵四边形ADCE是菱形,,,
∴,,
在Rt△AOD中,,
∴,
即,
∴.
21.【解答】解:(1)乙品种的平均数为(71+92+60+45+94+45+80+65+83+45)÷10=68(个),
甲品种的众数为65,
乙品种的中位数为68;
故答案为:68,65,68;
(2)增加甲品种的苹果种植面积更好,
理由:甲品种平均产量和乙品种一致,但甲品种方差更小,稳定性更好,同时它的众数和中位数均高于乙品种,大面积种植风险更小,故选甲;
(3)1500600(棵),
答:苹果产量在70个以上的苹果树约有600棵.
22.【解答】(1)证明:∵四边形ABCD是菱形,
∴OB=OD,
∵E是AD的中点,
∴OE是△ABD的中位线,
∴OE∥FG,
∵OG∥EF,
∴四边形OEFG是平行四边形,
∵EF⊥AB,
∴∠EFG=90°,
∴平行四边形OEFG是矩形;
(2)解:∵四边形ABCD是菱形,
∴AB=AD=10,AC⊥BD,
∴∠AOD=90°,
∵E是AD的中点,
∴,
由(1)可知,四边形EFCO是矩形,
∴FG=OE=5,
∵EF⊥AB,
∴∠EFA=90°,
∴,
∴BG=AB﹣AF﹣FG=10﹣3﹣5=2,
∵在直角三角形OGB中OB2=BG2+OG2=22+42=20,
∴,
∴.
23.【解答】(1)证明:∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∵BD+CD=BC,
∴CF+CD=BC;
(2)解:CF﹣CD=BC;理由如下:
∵∠BAC=90°,∠ABC=45°,
∴∠ACB=∠ABC=45°,
∴AB=AC,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAD=90°﹣∠DAC,∠CAF=90°﹣∠DAC,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
,
∴△BAD≌△CAF(SAS),
∴BD=CF,
∴BC+CD=CF,
∴CF﹣CD=BC;
(3)解:如图2,过点A作AN⊥BC,过点E作EH⊥CF,
∵,
∴,
∵AN⊥BC,
∴BN=CN=2,
∵∠ABC=45°,AN⊥BC,
∴AN=BN=2,
∵BC:CD=4:1,
∴CD=1,
∴ND=3,
由(2)知:△ABD≌△ACF,
∴BD=CF=BC+CD=5,∠ACF=∠B=45°,∠AFC=∠ADB,
∴∠BCF=∠ACB+∠ACF=90°,
∵∠B=45°,
∴BC=CG=4,
∴FG=1,
∵∠AFC+∠EFC=∠AFE=90°,∠ADB+∠DAN=90°,∠AFC=∠ADB,
∴∠DAN=∠EFC,
在△AND和△FHE中,
,
∴△AND≌△FHE(AAS),
∴EH=DN=3,HF=AN=2,
∴GH=FH﹣FG=1,
在直角三角形EHG中,由勾股定理得:.
24.【解答】解:(1)∵△ABC是等腰直角三角形,
∴S△ABCAB2,
∴AB2=10,
∵AO2+BO2=AB2,
∴9+BO2=10,
∴BO=1,
∵点B在x轴的负半轴,
∴m=﹣1;
(2)如图2,延长CE,AB交于点H,
∵y轴平分∠BAC,
∴∠CAE=∠HAE,
在△AEH和△AEC中,
,
∴△AEH≌△AEC(ASA),
∴HE=EC,
∴CH=2EC,
∵∠H+∠HAE=90°,∠H+∠HCB=90°,
∴∠HAE=∠HCE,
又∵AB=BC,∠ABC=∠CBH=90°,
∴△ABD≌△CBH(ASA),
∴AD=CH=2CE,
∴2;
(3)如图3,过点C作CP⊥x轴于P,
∵∠ABO+∠CBP=90°,∠ABO+∠BAO=90°,
∴∠BAO=∠CBP,
又∵∠AOB=∠BPC=90°,AB=BC,
∴△ABO≌△BCP(AAS),
∴BO=CP=﹣m,AO=BP=3,
∴OP=m+3,
∴点C坐标为(m+3,m),
∴点C在直线y=x﹣3上运动,
如图,直线y=x﹣3与x轴交于点K,与y轴交于点M,过点O作MK的对称点N,连接ON交直线MK于点F,连接AN交MK于点C',即点C'为所求点,
∴点M(0,﹣3),点N(3,0),
∴OM=OK,
∵点O,点N关于直线MK对称,
∴OF⊥MK,OF=FN,
∴点F(,),
∴点N(3,﹣3),
∴直线AN解析式为:y=﹣2x+3,
联立方程组,
解得,
∴点C坐标为(2,﹣1).
25.【解答】解:(1)∵四边形OABC为矩形,A(10,0),C(0,3),动点P在线段BC上以每秒2个单位长的速度由点C向B运动,点P的运动时间为t,
∴CB=OA=10,AB=OC=3,∠B=∠OAB=∠OCB=90°,CB∥OA,
∵点D是OA的中点,
∴,
由题意得:CP=2t,
∴PB=CB﹣CP=10﹣2t,
∵四边形PODB是平行四边形,
∴PB=OD=5,
∴10﹣2t=5,
∴t=2.5,
故答案为:2.5;
(2)在线段BC上存在一点Q,使得O,D,Q,P四点为顶点的四边形是菱形;理由如下:
分两种情况讨论:
①如图,当Q点在P的右边时,
∵四边形ODQP为菱形,
∴OP=PQ=OD=5,
在Rt△OPC中,由勾股定理得:,
∴2t=4,
∴t=2,
∵CQ=CP+PQ=4+5=9,
∴Q(9,3);
②如图2,当Q点在P的左边时,
∵四边形ODQP为菱形,
∴OQ=PQ=OD=5,
在Rt△OCQ中,,
∴CP=CQ+PQ=4+5=9,
∴2t=9,
∴t=4.5,
∵CQ=4,
∴Q(4,3);
综上所述,t=2秒时,Q(9,3);t=4.5秒时,Q(4,3);
(3)如图3,由(1)知:OD=5,
∵PM=5,
∴OD=PM,
∵CB∥OA,
∴四边形OPMD是平行四边形,
∴OP=DM,
∵四边形OAMP的周长为:
OA+AM+PM+OP
=10+AM+5+DM
=15+AM+DM,
∴AM+DM最小时,四边形OAMP的周长最小,
∴作点A关于BC的对称点E,连接DE交PB于M,
∴AM=EM,
∴AM+DM=DM+EM,
∵两点之间线段最短,
∴此时DM+EM最小,即AM+DM最小,
∵AE=AB+BE=3+3=6,
∴AM+DM的最小值为:,
∴四边形OAMP的周长最小值为.
21世纪教育网(www.21cnjy.com)
同课章节目录
