北师大版2024—2025学年七年级下学期数学期末复习强化提分练习(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下学期数学期末复习强化提分练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 927.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览




文档简介
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
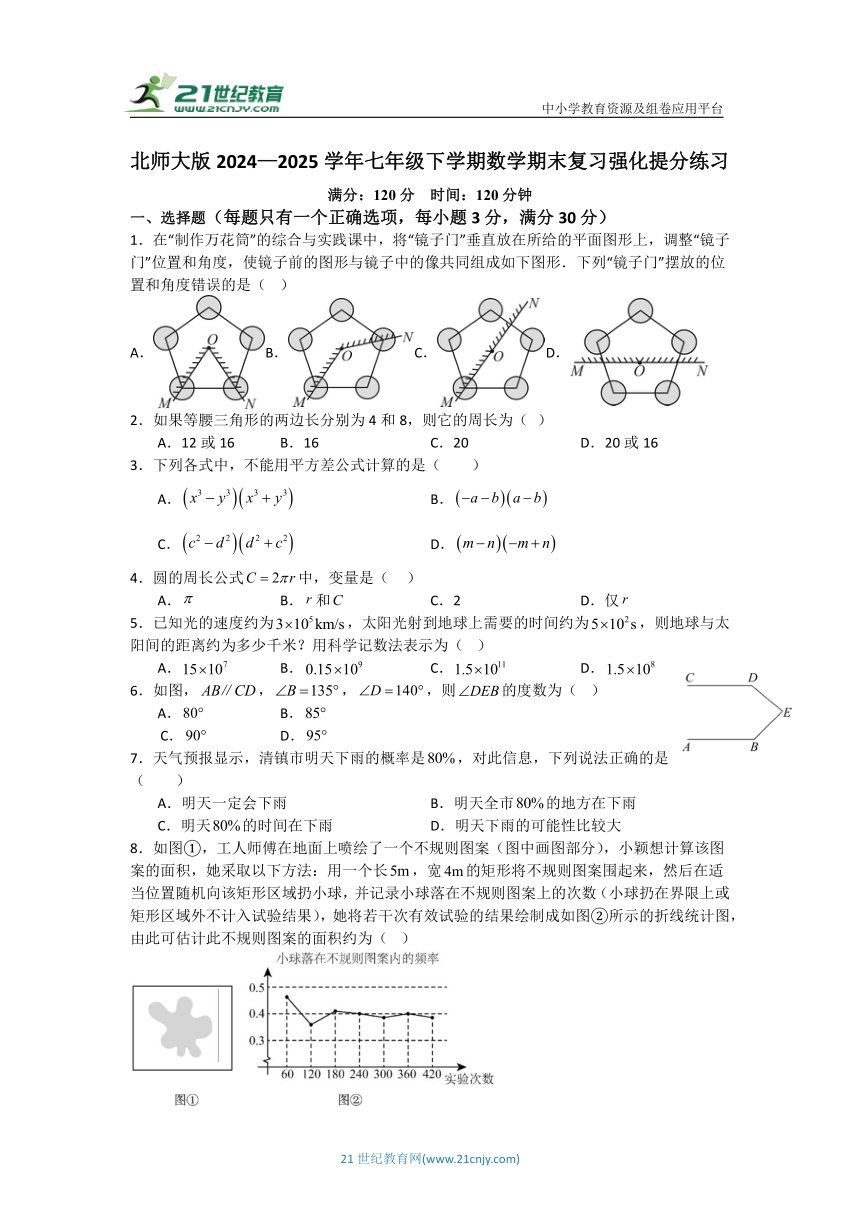
1.在“制作万花筒”的综合与实践课中,将“镜子门”垂直放在所给的平面图形上,调整“镜子门”位置和角度,使镜子前的图形与镜子中的像共同组成如下图形.下列“镜子门”摆放的位置和角度错误的是( )
A.B.C.D.
2.如果等腰三角形的两边长分别为4和8,则它的周长为( )
A.12或16 B.16 C.20 D.20或16
3.下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
4.圆的周长公式中,变量是( )
A. B.和 C.2 D.仅
5.已知光的速度约为,太阳光射到地球上需要的时间约为,则地球与太阳间的距离约为多少千米?用科学记数法表示为( )
A. B. C. D.
6.如图,,,,则的度数为( )
B.
C. D.
7.天气预报显示,清镇市明天下雨的概率是,对此信息,下列说法正确的是( )
A.明天一定会下雨 B.明天全市的地方在下雨
C.明天的时间在下雨 D.明天下雨的可能性比较大
8.如图①,工人师傅在地面上喷绘了一个不规则图案(图中画图部分),小颖想计算该图案的面积,她采取以下方法:用一个长,宽的矩形将不规则图案围起来,然后在适当位置随机向该矩形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界限上或矩形区域外不计入试验结果),她将若干次有效试验的结果绘制成如图②所示的折线统计图,由此可估计此不规则图案的面积约为( )
A. B. C. D.无法确定
9.若展开后不含x的一次项,则p与q的关系是( )
A. B. C. D.
10.如图,在中,,,,直线垂直平分线段,若点为边的中点,点为直线上一动点,连接、,则的周长的最小值为( )
A.13 B.12
C.11 D.10
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.某书店对外租赁图书,收费办法是:每本书在租赁后的头两天每天按0.5元收费,以后每天按0.7元收费(不足一天按一天计算)(元)和租赁天数(x≥2)之间的关系式为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
16.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
第II卷
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1) (2)
18.先化简,再求值:,其中,.
19.若多项式与的乘积中不含x的一次项.
(1)求的值;
(2)若,求的值.
20.一个不透明的盒子里装有4颗薄荷糖、5颗巧克力糖和1颗草莓糖,除颜色外完全相同.
(1)随机摸出一颗糖是薄荷糖的概率是多少?
(2)若从盒中取出若干颗薄荷糖,并放入相同数量的草莓糖,调整后随机摸出一颗是草莓糖的概率为.问取走了多少颗薄荷糖?
21.如图,在四边形中,,平分,E是上一点,交于点F.
(1)求的大小;
(2)若,求的大小.
22.已知琳琳家、超市、邮局在同一直线上,琳琳从家出发,跑步去超市买了土特产品,又步行去邮局把物品寄出,然后走回家.琳琳离家的距离与时间之间的关系如图所示.
请根据图象解决下列问题:
(1)琳琳家离超市的距离为______;
(2)琳琳邮寄物品用了______;
(3)求琳琳从邮局走回家的速度是多少?
23.如图,在边长为单位1的正方形网格中有,点A,B,C均在格点上.
(1)在图中作出关于直线l对称的(和A对应,和B对应,和C对应);
(2)求的面积;
(3)在直线l上作点P,使的值最小.
24.教科书第一章《整式的乘除》中,我们学习了整式的几种乘除运算,学会了研究运算的方法.现定义了一种新运算“”,对于任意有理数,,,规定.例如:.
请解答下列问题:
(1)填空: = ;
(2)若的代数式中不含的一次项时,求的值;
(3)如图1,在六边形中,对角线和相交于点,当四边形和四边形都为正方形时,设正方形和正方形的边长分别为,,若,,求出阴影部分的面积.
(4)如图2,小长方形长为,宽为,用张图中的小长方形按照图方式不重叠地放在大长方形内,其中,大长方形中未被覆盖的两个部分图中阴影部分,设左下角长方形的面积为,右上角长方形的面积为,当时,求的值.
25.已知是一条折线段,且,为平行线间的一点.
(1)如图1,若,求的度数;
(2)如图2,作的平分线交直线于点F,若,,求证:;
(3)如图3,作的平分线交直线于点F,射线交直线于点M,且为射线上一动点,连接的平分线交直线于点Q.设,请直接写出与的数量关系.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B D B D B B B
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:y与x的关系式为y=45﹣6x.
故答案为:y=45﹣6x.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
故答案为:15.
14.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
15.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
16.【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题
17.【解】(1)解:原式
;
(2)原式;
.
18.【解】解:
当,时,
原式.
19.【解】(1)解:
,
∵多项式乘积中不含x的一次项,
∴,
∴
∴
;
(2)解:∵
∴,
∴,
∴,
解得:,
∴
.
20.【解】(1)解:∵一个不透明的盒子里装有4颗薄荷糖、5颗巧克力糖和1颗草莓糖,且每颗糖被摸出的概率相同,
∴随机摸出一颗糖是薄荷糖的概率为;
(2)解:设取走了x颗薄荷糖.
由题意得,,
解得,
答:取走了2颗薄荷糖.
21.【解】(1)解:∵,
∴,
∴,
∵平分,
∴,
∴;
(2)∵,
∴,
∵,
∴,
∴,
∴.
22.【解】(1)解:由所给图象可知,超市离琳琳家.
故答案为:.
(2)解:由题意,,
琳琳在邮局停留了,即琳琳邮寄物品用了.
故答案为:.
(3)解:由图象可得,邮局离琳琳家距离为,琳琳走的时间为:,,
答:琳琳从邮局走回家的速度是.
23.【解】(1)解:如图所示,即为所求;
(2)解:;
(3)解:如图所示,点P即为所求;
24.【解】(1)解:根据新运算,
对于;
故答案为:.
(2),
∵代数式中不含x的一次项,
∴一次项系数,
∴解得;
(3),
可得:,
即,
∴,
∵,
∴,
∴,
∴,
阴影部分面积为两个三角形面积和;
(4)∵,
∴,,
∵
∴,
即,
∴
.
25.【解】(1)解:如图,过点作的平行线,
,,
,,
,
;
(2)解:,
,
是的平分线,
,
,,
,
;
(3)解:当点在点左边时,如图,
,,平分,
,
平分,
,
,
,
平分,
,
,即;
当点在点右边时,如图,
,,
平分,
,
,
,即,
综上,或.
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在“制作万花筒”的综合与实践课中,将“镜子门”垂直放在所给的平面图形上,调整“镜子门”位置和角度,使镜子前的图形与镜子中的像共同组成如下图形.下列“镜子门”摆放的位置和角度错误的是( )
A.B.C.D.
2.如果等腰三角形的两边长分别为4和8,则它的周长为( )
A.12或16 B.16 C.20 D.20或16
3.下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
4.圆的周长公式中,变量是( )
A. B.和 C.2 D.仅
5.已知光的速度约为,太阳光射到地球上需要的时间约为,则地球与太阳间的距离约为多少千米?用科学记数法表示为( )
A. B. C. D.
6.如图,,,,则的度数为( )
B.
C. D.
7.天气预报显示,清镇市明天下雨的概率是,对此信息,下列说法正确的是( )
A.明天一定会下雨 B.明天全市的地方在下雨
C.明天的时间在下雨 D.明天下雨的可能性比较大
8.如图①,工人师傅在地面上喷绘了一个不规则图案(图中画图部分),小颖想计算该图案的面积,她采取以下方法:用一个长,宽的矩形将不规则图案围起来,然后在适当位置随机向该矩形区域扔小球,并记录小球落在不规则图案上的次数(小球扔在界限上或矩形区域外不计入试验结果),她将若干次有效试验的结果绘制成如图②所示的折线统计图,由此可估计此不规则图案的面积约为( )
A. B. C. D.无法确定
9.若展开后不含x的一次项,则p与q的关系是( )
A. B. C. D.
10.如图,在中,,,,直线垂直平分线段,若点为边的中点,点为直线上一动点,连接、,则的周长的最小值为( )
A.13 B.12
C.11 D.10
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.某书店对外租赁图书,收费办法是:每本书在租赁后的头两天每天按0.5元收费,以后每天按0.7元收费(不足一天按一天计算)(元)和租赁天数(x≥2)之间的关系式为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
16.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
第II卷
北师大版2024—2025学年七年级下学期数学期末复习强化提分练习
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:
(1) (2)
18.先化简,再求值:,其中,.
19.若多项式与的乘积中不含x的一次项.
(1)求的值;
(2)若,求的值.
20.一个不透明的盒子里装有4颗薄荷糖、5颗巧克力糖和1颗草莓糖,除颜色外完全相同.
(1)随机摸出一颗糖是薄荷糖的概率是多少?
(2)若从盒中取出若干颗薄荷糖,并放入相同数量的草莓糖,调整后随机摸出一颗是草莓糖的概率为.问取走了多少颗薄荷糖?
21.如图,在四边形中,,平分,E是上一点,交于点F.
(1)求的大小;
(2)若,求的大小.
22.已知琳琳家、超市、邮局在同一直线上,琳琳从家出发,跑步去超市买了土特产品,又步行去邮局把物品寄出,然后走回家.琳琳离家的距离与时间之间的关系如图所示.
请根据图象解决下列问题:
(1)琳琳家离超市的距离为______;
(2)琳琳邮寄物品用了______;
(3)求琳琳从邮局走回家的速度是多少?
23.如图,在边长为单位1的正方形网格中有,点A,B,C均在格点上.
(1)在图中作出关于直线l对称的(和A对应,和B对应,和C对应);
(2)求的面积;
(3)在直线l上作点P,使的值最小.
24.教科书第一章《整式的乘除》中,我们学习了整式的几种乘除运算,学会了研究运算的方法.现定义了一种新运算“”,对于任意有理数,,,规定.例如:.
请解答下列问题:
(1)填空: = ;
(2)若的代数式中不含的一次项时,求的值;
(3)如图1,在六边形中,对角线和相交于点,当四边形和四边形都为正方形时,设正方形和正方形的边长分别为,,若,,求出阴影部分的面积.
(4)如图2,小长方形长为,宽为,用张图中的小长方形按照图方式不重叠地放在大长方形内,其中,大长方形中未被覆盖的两个部分图中阴影部分,设左下角长方形的面积为,右上角长方形的面积为,当时,求的值.
25.已知是一条折线段,且,为平行线间的一点.
(1)如图1,若,求的度数;
(2)如图2,作的平分线交直线于点F,若,,求证:;
(3)如图3,作的平分线交直线于点F,射线交直线于点M,且为射线上一动点,连接的平分线交直线于点Q.设,请直接写出与的数量关系.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D B D B D B B B
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:y与x的关系式为y=45﹣6x.
故答案为:y=45﹣6x.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
故答案为:15.
14.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
15.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
16.【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题
17.【解】(1)解:原式
;
(2)原式;
.
18.【解】解:
当,时,
原式.
19.【解】(1)解:
,
∵多项式乘积中不含x的一次项,
∴,
∴
∴
;
(2)解:∵
∴,
∴,
∴,
解得:,
∴
.
20.【解】(1)解:∵一个不透明的盒子里装有4颗薄荷糖、5颗巧克力糖和1颗草莓糖,且每颗糖被摸出的概率相同,
∴随机摸出一颗糖是薄荷糖的概率为;
(2)解:设取走了x颗薄荷糖.
由题意得,,
解得,
答:取走了2颗薄荷糖.
21.【解】(1)解:∵,
∴,
∴,
∵平分,
∴,
∴;
(2)∵,
∴,
∵,
∴,
∴,
∴.
22.【解】(1)解:由所给图象可知,超市离琳琳家.
故答案为:.
(2)解:由题意,,
琳琳在邮局停留了,即琳琳邮寄物品用了.
故答案为:.
(3)解:由图象可得,邮局离琳琳家距离为,琳琳走的时间为:,,
答:琳琳从邮局走回家的速度是.
23.【解】(1)解:如图所示,即为所求;
(2)解:;
(3)解:如图所示,点P即为所求;
24.【解】(1)解:根据新运算,
对于;
故答案为:.
(2),
∵代数式中不含x的一次项,
∴一次项系数,
∴解得;
(3),
可得:,
即,
∴,
∵,
∴,
∴,
∴,
阴影部分面积为两个三角形面积和;
(4)∵,
∴,,
∵
∴,
即,
∴
.
25.【解】(1)解:如图,过点作的平行线,
,,
,,
,
;
(2)解:,
,
是的平分线,
,
,,
,
;
(3)解:当点在点左边时,如图,
,,平分,
,
平分,
,
,
,
平分,
,
,即;
当点在点右边时,如图,
,,
平分,
,
,
,即,
综上,或.
同课章节目录
