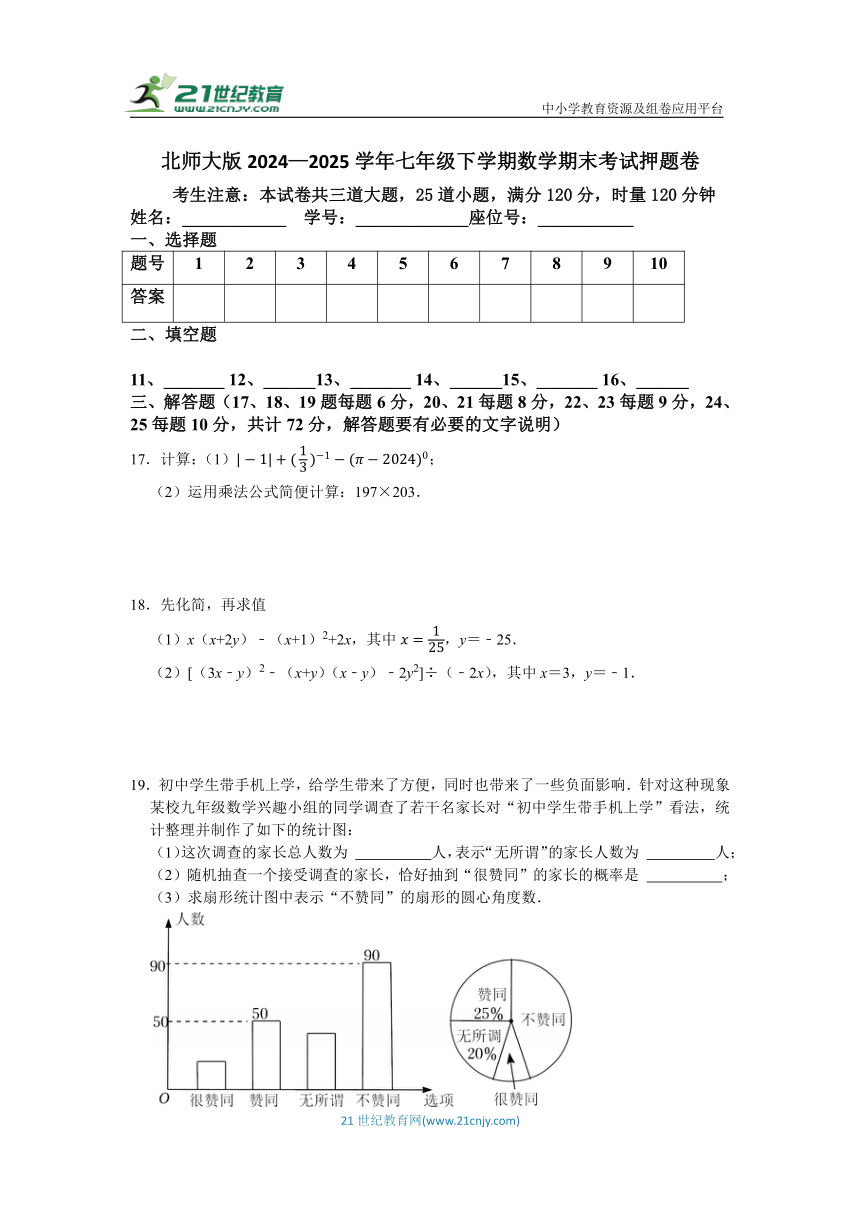
北师大版2024—2025学年七年级下学期数学期末考试押题卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下学期数学期末考试押题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 831.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 12:51:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下学期数学期末考试押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.汉字是中华文明的标志,每种字体都有着各自鲜明的艺术特征.下面的小篆体字是轴对称图形的是( )
A. B. C. D.
2.某遥感卫星每秒向地面站传回的数据量为比特.后续发射的升级型号卫星数据传输速率是原遥感卫星的25倍,达到比特,则的值为( )
A. B. C. D.
3.若,则的值为( )
A.1 B. C.6 D.
4.如图,有三张边长分别为a,b,c的正方形纸片A,B,C,将三张纸片按图1,图2两种不同方式放置于同一长方形中.记图1中阴影部分周长为,面积为;图2中阴影部分周长为,面积为,若,则b与c满足的关系为( )
A. B. C. D.
5.下列各式不能使用平方差公式的是( )
A. B.
C. D.
6.端午节到了,小红煮好了10个粽子,其中有6个红枣粽子,4个绿豆粽子.小红想从煮好的粽子中随机捞一个,若每个粽子形状大小完全相同,被捞到的机会相等,则她捞到红枣粽子的概率是( )
A. B. C. D.
7.如图,相交于点,且,添加下列条件,仍无法判定的是( )
A. B. C. D.
8.某商品的售价x(元)与销量y(件)之间存在如下关系,估计当售价x为137元时,销量y可能为( )
售价x/元 90 100 110 120 130 140
销量y/件 90 80 70 60 50 40
A.33件 B.43件 C.53件 D.63件
9.如图,在中, 垂直平分边,若的周长为,,则的长为( )
A. B. C. D.
10.如图,在中,,,面积是12,的垂直平分线分别交,边于点E,F.若点D为边的中点,点P为线段上一动点,则周长的最小值是( )
A.8 B.3 C.6 D.4
二、填空题(每小题3分,满分18分)
11.若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .
12.如图,在△ABC中,AD平分∠BAC,DE=1,则S△ACD= .
13.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨)(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),则抽到的节气在夏季的概率为 .
14.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置点A、B分别落在直线m、n上.若∠1=70°,则∠2的度数为 .
15.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=60°,∠C=40°,则∠DAE= 度.
16.如图,在△ABC中,∠ACB=90°,∠A=26°,点D是AC边上一动点,将△ABD沿直线BD翻折,使点A落在点F处,连接BF,交AC于点E,当△DEF是直角三角形时,则∠BDC的度数为 .
北师大版2024—2025学年七年级下学期数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:(1);
(2)运用乘法公式简便计算:197×203.
18.先化简,再求值
(1)x(x+2y)﹣(x+1)2+2x,其中,y=﹣25.
(2)[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷(﹣2x),其中x=3,y=﹣1.
19.初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总人数为 人,表示“无所谓”的家长人数为 人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是 ;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
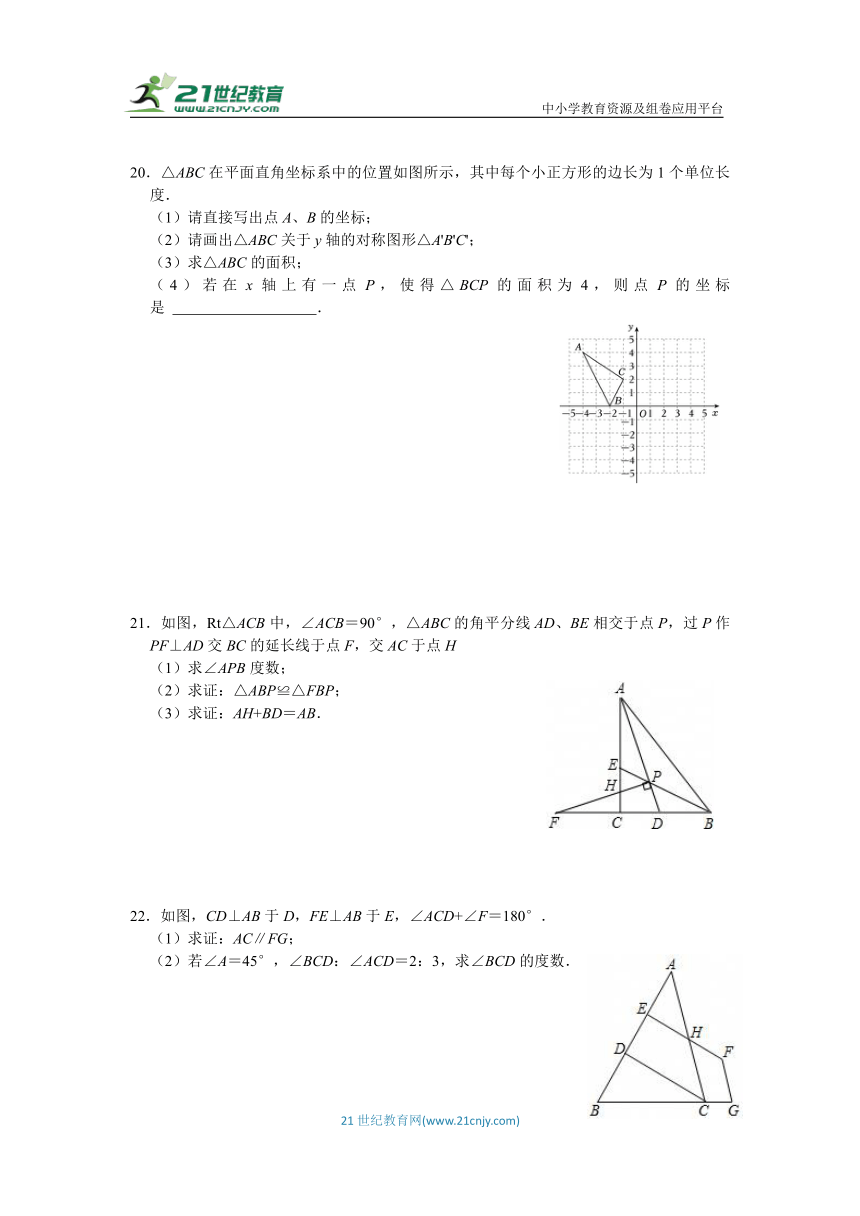
20.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)请直接写出点A、B的坐标;
(2)请画出△ABC关于y轴的对称图形△A'B'C';
(3)求△ABC的面积;
(4)若在x轴上有一点P,使得△BCP的面积为4,则点P的坐标是 .
21.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
22.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
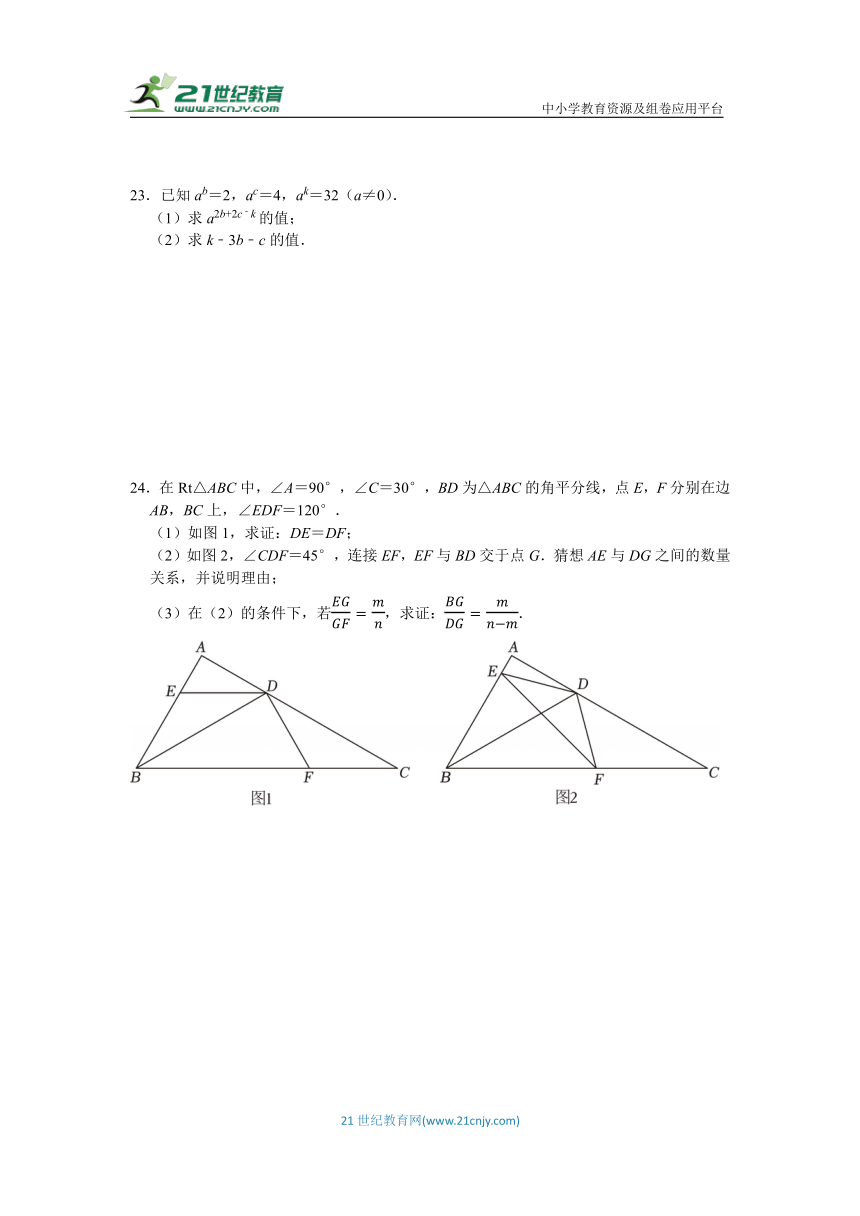
23.已知ab=2,ac=4,ak=32(a≠0).
(1)求a2b+2c﹣k的值;
(2)求k﹣3b﹣c的值.
24.在Rt△ABC中,∠A=90°,∠C=30°,BD为△ABC的角平分线,点E,F分别在边AB,BC上,∠EDF=120°.
(1)如图1,求证:DE=DF;
(2)如图2,∠CDF=45°,连接EF,EF与BD交于点G.猜想AE与DG之间的数量关系,并说明理由;
(3)在(2)的条件下,若,求证:.
25.已知直线EF与直线AB、CD分别交于E、F两点,∠BEF和∠DFE的角平分线交于点P,且∠BEP+∠DFP=90°.
(1)求证:AB∥CD;
(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;
(3)如图3,若∠BEP=60°,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时开始旋转,当射线EP1∥FP2时,求满足条件的t的值为多少.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A C A C C B A A
二、填空题
11.【解答】解:①5是腰长时,三角形的三边分别为5、3,2,
能组成三角形,
周长=5+6+2=12,
②5是底边时,三角形的三边分别为7、2、5,
不能组成三角形,
故答案为:12.
12.【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,
∴DE=DF=1,
∵AC=2,
∴S△ACD=AC DF
=×2×1
=8,
故答案为:1.
13.【解答】解:从二十四个节气中选一个节气,则抽到的节气在夏季的概率为=,
故答案为:.
14.【解答】解:如图:
∵m∥n,
∴∠ABD=∠1=70°,
∴∠2=70°﹣30°=40°.
故答案为:40°.
15.【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
又∵AE平分∠BAC,
∴∠BAE∠BAC80°=40°.
∵AD是BC上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10.
16.【解答】解:由翻折得∠F=∠A=26°,∠ABD=∠EBD,
当△DEF为直角三角形,且∠EDF=90°时,如图1,
∴∠DEF=90°﹣∠F=90°﹣26°=64°,
∴∠ABE=∠DEF﹣∠F=64°﹣26°=38°,
∴,
∴∠BDC=∠ABD+∠A=19°+26°=45°;
当△DEF为直角三角形,且∠DEF=90° 时,如图2,此时点E与点C重合,
∴∠DEB=90°,且BE,CF共线,
∵∠ABE=90°﹣∠A=90°﹣26°=64°
∴,
∴∠BDC=90°﹣∠DBE=90°﹣32°=58°,
综上所述:∠BCD的度数为45°或58°,
故答案为:45°或58°.
三、解答题
17.【解答】解:(1)
=1+3﹣1
=3;
(2)197×203
=(200﹣3)(200+3)
=2002﹣32
=40000﹣9
=39991.
18.【解答】解:(1)x(x+2y)﹣(x+1)2+2x
=x2+2xy﹣x2﹣2x﹣1+2x
=2xy﹣1
当,y=﹣25时,
原式;
(2)[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷(﹣2x)
=[9x2﹣6xy+y2﹣x2+y2﹣2y2]÷(﹣2x)
=[8x2﹣6xy]÷(﹣2x)
=﹣4x+3y,
当x=3,y=﹣1时,
原式=﹣4×3+3×(﹣1)=﹣15.
19.【解答】解:(1)这次调查的家长总人数为:50÷25%=200(人),
表示“无所谓”的家长人数为:200×20%=40(人).
故答案为:200,40;
(2)“很赞同”的家长人数为:200﹣90﹣50﹣40=20(人),
抽到“很赞同”的家长的概率是20÷200.
故答案为:;
(3)“不赞同”的扇形的圆心角度数为:360°=162°.
20.【解答】解:(1)由图可得,A(﹣4,4),B(﹣2,0).
(2)如图,△A'B'C'即为所求.
(3)△ABC的面积为9﹣1﹣4=4.
(4)设点P的坐标是(m,0),
∵△BCP的面积为4,
∴4,
解得m=2或﹣6,
∴点P的坐标是(2,0)或(﹣6,0).
故答案为:(2,0)或(﹣6,0).
21.【解答】解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA(∠ABC+∠BAC)=45°,
∴∠APB=180°﹣45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
22.【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
23.【解答】解:(1)∵ab=2,ac=4,ak=32,
∴a2b+2c﹣k
=a2b a2c÷ak
=(ab)2 (ac)2÷ak
=22×42÷32
=4×16÷32
=2;
(2)ak﹣3b﹣c
=ak÷a3b÷ac
=ak÷(ab)3÷ac
=32÷23÷4
=32÷8÷4
=1,
∵ab=2,
∴a≠±1,
∵ak﹣3b﹣c=1(a≠0,a≠±1),
∴k﹣3b﹣c=0.
24.【解答】(1)证明:过D作DM⊥BC.
∵BD为△ABC的角平分线,
∴DM=DA.
∵∠C=30°,
∴∠MDF+∠FDC=60°,
∵∠EDF=120°,
∴∠ADE+∠FDC=60°,
∴∠ADE=∠MDF.
在△AED和△MDF中,
,
∴△AED≌△MDF(AAS),
∴DE=DF.
(2)过F作FQ⊥GD,过D作DM⊥BC.
由(1)知△AED≌△MDF,
∴MF=AE,∠MDF=∠ADE,
∵∠EDF=∠EDM+∠MDF=120°,
∴∠EDM+∠ADE=120°,
∠ADM=120°,
∵∠A=∠DMB=90°,∠ABD=∠DBM,
∴∠ADB=∠BDM,
∵∠ADB+∠BDM=∠ADM=120°,
∴∠ADB=∠BDM=60°,
∵∠FDC=45°,∠EDF=120°,
∴∠ADE=15°,
∴∠EDG=60°﹣15°=45°.
∴∠GDF=120°﹣45°=75°.
∵∠EDF=120°,DE=DF,
∴∠DEG=∠DFG=30°,
∴∠FGD=75°,
∴∠FDG=∠FGD,
∴FG=FD,
∴GD=2QD.
在△FQD和△DMF中,
,
∴△FQD≌△DMF(AAS),
∴QD=MF,
∴DG=2AE.
(3)过E作EN⊥BDD,过F作FH⊥BD,过D作DM⊥BC,DR⊥EF.
由(2)∠AED=90°﹣∠ADE=75°,
∴∠BEG=180°﹣∠AED﹣∠DEG=75°,
又∠EGB=∠DGF=75°,
∴∠BEG=∠BGE,
∴BE=BG,
同理:FG=FD.
∴.
设BE=mx,BF=nx,
∵∠BEG=∠BGE=75°,
∴BG=BE=mx,
同理:BD=BF=nx,
∴GD=BD﹣BG=nx﹣mx=(n﹣m)x,
∴.
25.【解答】解:(1)∵∠BEF和∠DFE的角平分线交于点P,
∴∠EBF=2∠BEP,∠DFE=2∠DFP,
∴∠EBF+∠DFE=2(∠BEP+∠DFP)=2×90°=180°,
∴AB∥CD.
(2)∵∠BEP+∠DFP=90°,又AB∥CD.
∴∠P=180﹣(∠PEF+∠PFE)=180°﹣(∠BEP+∠DFP)=90°,
由外角性质得:∠Q=∠MFQ﹣∠MEQ
=∠MFP﹣∠MEP
=(∠MFP﹣∠MEP)
=,
∵∠P=90°,
∴∠Q==45°.
(3)当FP2在EF右侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t+60°,∠EFP2=3t+30°,
∴15t+60°+3t+30°=180,
解得t=5.
当FP2在EF左侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t﹣60°,∠EFP2=3t﹣30°,
∴15t﹣60°+3t﹣30°=180°,
解得t=15,t=30
综上分析,t=5或t=15或30时,EP1∥FP2.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下学期数学期末考试押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.汉字是中华文明的标志,每种字体都有着各自鲜明的艺术特征.下面的小篆体字是轴对称图形的是( )
A. B. C. D.
2.某遥感卫星每秒向地面站传回的数据量为比特.后续发射的升级型号卫星数据传输速率是原遥感卫星的25倍,达到比特,则的值为( )
A. B. C. D.
3.若,则的值为( )
A.1 B. C.6 D.
4.如图,有三张边长分别为a,b,c的正方形纸片A,B,C,将三张纸片按图1,图2两种不同方式放置于同一长方形中.记图1中阴影部分周长为,面积为;图2中阴影部分周长为,面积为,若,则b与c满足的关系为( )
A. B. C. D.
5.下列各式不能使用平方差公式的是( )
A. B.
C. D.
6.端午节到了,小红煮好了10个粽子,其中有6个红枣粽子,4个绿豆粽子.小红想从煮好的粽子中随机捞一个,若每个粽子形状大小完全相同,被捞到的机会相等,则她捞到红枣粽子的概率是( )
A. B. C. D.
7.如图,相交于点,且,添加下列条件,仍无法判定的是( )
A. B. C. D.
8.某商品的售价x(元)与销量y(件)之间存在如下关系,估计当售价x为137元时,销量y可能为( )
售价x/元 90 100 110 120 130 140
销量y/件 90 80 70 60 50 40
A.33件 B.43件 C.53件 D.63件
9.如图,在中, 垂直平分边,若的周长为,,则的长为( )
A. B. C. D.
10.如图,在中,,,面积是12,的垂直平分线分别交,边于点E,F.若点D为边的中点,点P为线段上一动点,则周长的最小值是( )
A.8 B.3 C.6 D.4
二、填空题(每小题3分,满分18分)
11.若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .
12.如图,在△ABC中,AD平分∠BAC,DE=1,则S△ACD= .
13.二十四节气,它基本概括了一年中四季交替的准确时间以及大自然中一些物候等自然现象发生的规律,二十四个节气分别为:春季(立春、雨水、惊蛰、春分、清明、谷雨)(立夏、小满、芒种、夏至、小暑、大暑),秋季(立秋、处暑、白露、秋分、寒露、霜降),冬季(立冬、小雪、大雪、冬至、小寒、大寒),则抽到的节气在夏季的概率为 .
14.已知直线m∥n,将一块含30°角的直角三角板ABC按如图方式放置点A、B分别落在直线m、n上.若∠1=70°,则∠2的度数为 .
15.如图,△ABC中,AD是BC上的高,AE平分∠BAC,∠B=60°,∠C=40°,则∠DAE= 度.
16.如图,在△ABC中,∠ACB=90°,∠A=26°,点D是AC边上一动点,将△ABD沿直线BD翻折,使点A落在点F处,连接BF,交AC于点E,当△DEF是直角三角形时,则∠BDC的度数为 .
北师大版2024—2025学年七年级下学期数学期末考试押题卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:(1);
(2)运用乘法公式简便计算:197×203.
18.先化简,再求值
(1)x(x+2y)﹣(x+1)2+2x,其中,y=﹣25.
(2)[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷(﹣2x),其中x=3,y=﹣1.
19.初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总人数为 人,表示“无所谓”的家长人数为 人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是 ;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
20.△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.
(1)请直接写出点A、B的坐标;
(2)请画出△ABC关于y轴的对称图形△A'B'C';
(3)求△ABC的面积;
(4)若在x轴上有一点P,使得△BCP的面积为4,则点P的坐标是 .
21.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
22.如图,CD⊥AB于D,FE⊥AB于E,∠ACD+∠F=180°.
(1)求证:AC∥FG;
(2)若∠A=45°,∠BCD:∠ACD=2:3,求∠BCD的度数.
23.已知ab=2,ac=4,ak=32(a≠0).
(1)求a2b+2c﹣k的值;
(2)求k﹣3b﹣c的值.
24.在Rt△ABC中,∠A=90°,∠C=30°,BD为△ABC的角平分线,点E,F分别在边AB,BC上,∠EDF=120°.
(1)如图1,求证:DE=DF;
(2)如图2,∠CDF=45°,连接EF,EF与BD交于点G.猜想AE与DG之间的数量关系,并说明理由;
(3)在(2)的条件下,若,求证:.
25.已知直线EF与直线AB、CD分别交于E、F两点,∠BEF和∠DFE的角平分线交于点P,且∠BEP+∠DFP=90°.
(1)求证:AB∥CD;
(2)如图2,∠PEF和∠PFM的角平分线交于点Q,求∠Q的度数;
(3)如图3,若∠BEP=60°,延长线段EP得射线EP1,延长线段FP得射线FP2,射线EP1绕点E以每秒15°的速度逆时针旋转360°后停止,射线FP2绕点F以每秒3°的速度顺时针旋转180°以后停止.设它们同时开始旋转,当射线EP1∥FP2时,求满足条件的t的值为多少.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A C A C C B A A
二、填空题
11.【解答】解:①5是腰长时,三角形的三边分别为5、3,2,
能组成三角形,
周长=5+6+2=12,
②5是底边时,三角形的三边分别为7、2、5,
不能组成三角形,
故答案为:12.
12.【解答】解:过点D作DF⊥AC,垂足为F,
∵AD平分∠BAC,DE⊥AB,
∴DE=DF=1,
∵AC=2,
∴S△ACD=AC DF
=×2×1
=8,
故答案为:1.
13.【解答】解:从二十四个节气中选一个节气,则抽到的节气在夏季的概率为=,
故答案为:.
14.【解答】解:如图:
∵m∥n,
∴∠ABD=∠1=70°,
∴∠2=70°﹣30°=40°.
故答案为:40°.
15.【解答】解:在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°﹣∠B﹣∠C=180°﹣60°﹣40°=80°,
又∵AE平分∠BAC,
∴∠BAE∠BAC80°=40°.
∵AD是BC上的高,
∴∠ADB=90°,
∴∠BAD=90°﹣∠B=90°﹣60°=30°,
∴∠DAE=∠BAE﹣∠BAD=40°﹣30°=10°.
故答案为:10.
16.【解答】解:由翻折得∠F=∠A=26°,∠ABD=∠EBD,
当△DEF为直角三角形,且∠EDF=90°时,如图1,
∴∠DEF=90°﹣∠F=90°﹣26°=64°,
∴∠ABE=∠DEF﹣∠F=64°﹣26°=38°,
∴,
∴∠BDC=∠ABD+∠A=19°+26°=45°;
当△DEF为直角三角形,且∠DEF=90° 时,如图2,此时点E与点C重合,
∴∠DEB=90°,且BE,CF共线,
∵∠ABE=90°﹣∠A=90°﹣26°=64°
∴,
∴∠BDC=90°﹣∠DBE=90°﹣32°=58°,
综上所述:∠BCD的度数为45°或58°,
故答案为:45°或58°.
三、解答题
17.【解答】解:(1)
=1+3﹣1
=3;
(2)197×203
=(200﹣3)(200+3)
=2002﹣32
=40000﹣9
=39991.
18.【解答】解:(1)x(x+2y)﹣(x+1)2+2x
=x2+2xy﹣x2﹣2x﹣1+2x
=2xy﹣1
当,y=﹣25时,
原式;
(2)[(3x﹣y)2﹣(x+y)(x﹣y)﹣2y2]÷(﹣2x)
=[9x2﹣6xy+y2﹣x2+y2﹣2y2]÷(﹣2x)
=[8x2﹣6xy]÷(﹣2x)
=﹣4x+3y,
当x=3,y=﹣1时,
原式=﹣4×3+3×(﹣1)=﹣15.
19.【解答】解:(1)这次调查的家长总人数为:50÷25%=200(人),
表示“无所谓”的家长人数为:200×20%=40(人).
故答案为:200,40;
(2)“很赞同”的家长人数为:200﹣90﹣50﹣40=20(人),
抽到“很赞同”的家长的概率是20÷200.
故答案为:;
(3)“不赞同”的扇形的圆心角度数为:360°=162°.
20.【解答】解:(1)由图可得,A(﹣4,4),B(﹣2,0).
(2)如图,△A'B'C'即为所求.
(3)△ABC的面积为9﹣1﹣4=4.
(4)设点P的坐标是(m,0),
∵△BCP的面积为4,
∴4,
解得m=2或﹣6,
∴点P的坐标是(2,0)或(﹣6,0).
故答案为:(2,0)或(﹣6,0).
21.【解答】解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA(∠ABC+∠BAC)=45°,
∴∠APB=180°﹣45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
22.【解答】(1)证明:∵CD⊥AB,FE⊥AB,
∴∠AEH=∠ADC=90°,
∴EF∥DC,
∴∠AHE=∠ACD,
∵∠ACD+∠F=180°.
∴∠AHE+∠F=180°,
∵∠AHE+∠EHC=180°,
∴∠EHC=∠F,
∴AC∥FG;
(2)解:∵∠BCD:∠ACD=2:3,
∴设∠BCD=2x,∠ACD=3x,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A+∠ACD=90°,
∴解得x=15°,
∴∠BCD=2x=30°.
答:∠BCD的度数为30°.
23.【解答】解:(1)∵ab=2,ac=4,ak=32,
∴a2b+2c﹣k
=a2b a2c÷ak
=(ab)2 (ac)2÷ak
=22×42÷32
=4×16÷32
=2;
(2)ak﹣3b﹣c
=ak÷a3b÷ac
=ak÷(ab)3÷ac
=32÷23÷4
=32÷8÷4
=1,
∵ab=2,
∴a≠±1,
∵ak﹣3b﹣c=1(a≠0,a≠±1),
∴k﹣3b﹣c=0.
24.【解答】(1)证明:过D作DM⊥BC.
∵BD为△ABC的角平分线,
∴DM=DA.
∵∠C=30°,
∴∠MDF+∠FDC=60°,
∵∠EDF=120°,
∴∠ADE+∠FDC=60°,
∴∠ADE=∠MDF.
在△AED和△MDF中,
,
∴△AED≌△MDF(AAS),
∴DE=DF.
(2)过F作FQ⊥GD,过D作DM⊥BC.
由(1)知△AED≌△MDF,
∴MF=AE,∠MDF=∠ADE,
∵∠EDF=∠EDM+∠MDF=120°,
∴∠EDM+∠ADE=120°,
∠ADM=120°,
∵∠A=∠DMB=90°,∠ABD=∠DBM,
∴∠ADB=∠BDM,
∵∠ADB+∠BDM=∠ADM=120°,
∴∠ADB=∠BDM=60°,
∵∠FDC=45°,∠EDF=120°,
∴∠ADE=15°,
∴∠EDG=60°﹣15°=45°.
∴∠GDF=120°﹣45°=75°.
∵∠EDF=120°,DE=DF,
∴∠DEG=∠DFG=30°,
∴∠FGD=75°,
∴∠FDG=∠FGD,
∴FG=FD,
∴GD=2QD.
在△FQD和△DMF中,
,
∴△FQD≌△DMF(AAS),
∴QD=MF,
∴DG=2AE.
(3)过E作EN⊥BDD,过F作FH⊥BD,过D作DM⊥BC,DR⊥EF.
由(2)∠AED=90°﹣∠ADE=75°,
∴∠BEG=180°﹣∠AED﹣∠DEG=75°,
又∠EGB=∠DGF=75°,
∴∠BEG=∠BGE,
∴BE=BG,
同理:FG=FD.
∴.
设BE=mx,BF=nx,
∵∠BEG=∠BGE=75°,
∴BG=BE=mx,
同理:BD=BF=nx,
∴GD=BD﹣BG=nx﹣mx=(n﹣m)x,
∴.
25.【解答】解:(1)∵∠BEF和∠DFE的角平分线交于点P,
∴∠EBF=2∠BEP,∠DFE=2∠DFP,
∴∠EBF+∠DFE=2(∠BEP+∠DFP)=2×90°=180°,
∴AB∥CD.
(2)∵∠BEP+∠DFP=90°,又AB∥CD.
∴∠P=180﹣(∠PEF+∠PFE)=180°﹣(∠BEP+∠DFP)=90°,
由外角性质得:∠Q=∠MFQ﹣∠MEQ
=∠MFP﹣∠MEP
=(∠MFP﹣∠MEP)
=,
∵∠P=90°,
∴∠Q==45°.
(3)当FP2在EF右侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t+60°,∠EFP2=3t+30°,
∴15t+60°+3t+30°=180,
解得t=5.
当FP2在EF左侧时,EP1∥FP2时,∠P1EF+∠EFP2=180°,
根据题意可知:∠P1EF=15t﹣60°,∠EFP2=3t﹣30°,
∴15t﹣60°+3t﹣30°=180°,
解得t=15,t=30
综上分析,t=5或t=15或30时,EP1∥FP2.
21世纪教育网(www.21cnjy.com)
同课章节目录
