北师大版2024—2025学年七年级下册数学期末素养检测卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下册数学期末素养检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 771.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 12:52:04 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下册数学期末素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
选择题(每题只有一个正确选项,每小题3分,满分30分)
1.正方形的周长C与其边长a的函数关系式为,其中常量是( )
A.4 B.a C.C D.
2.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅图案分别代表“立春、立夏、芒种、大雪”,其中不是轴对称图形的是( )
A. B. C. D.
3.经过近60年的发展,我国已建成目前世界上技术手段最为完 备的国家授时系统,授时精度从开始的毫秒级(千分之一秒)到了如今的百皮秒级(百亿分之一秒),提高了7个数量级,处于世界领先水平.已知1秒毫秒,1毫秒皮秒,则10秒等于( )
A.皮秒 B.皮秒 C.皮秒 D.皮秒
4.若的乘积中不含项,则常数m的值为( )
A.5 B. C. D.
5.下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
6.如图,有三张边长分别为,,的正方形纸片,,,将三张纸片按图1,图2两种不同方式放置于同一长方形中.记图1中阴影部分周长为,面积为;图2中阴影部分周长为,面积为,若,则与满足的关系为( )
A. B. C. D.
7.下列说法不正确的是( )
A.为了了解春节联欢晚会的收视率,选择抽样调查
B.为了审核书稿中的错别字,选择全面调查
C.“经过交通信号灯的路口,遇到红灯”是必然事件
D.“射击运动员射击一次命中靶心”是随机事件
8.下面每组中的三条线段,能围成三角形的是( )
A. B. C. D.
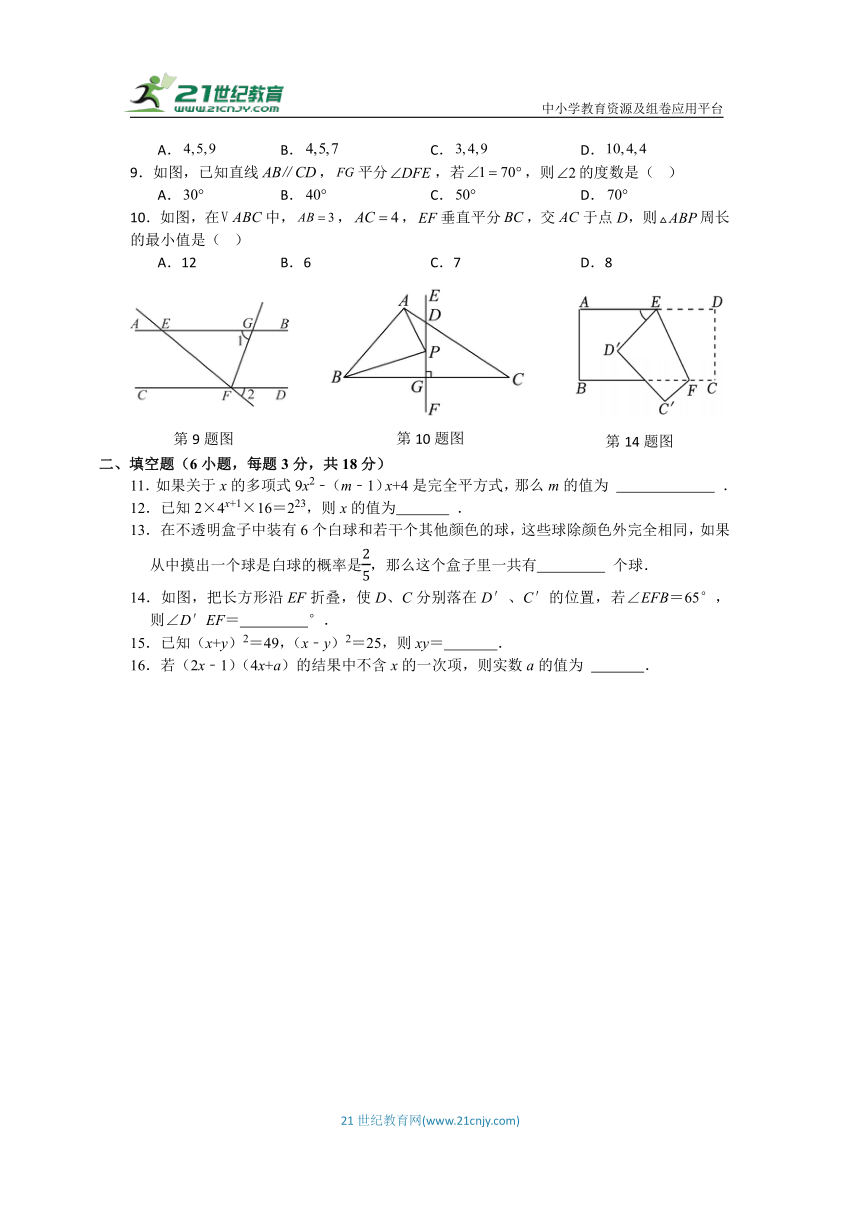
9.如图,已知直线,平分,若,则的度数是( )
A. B. C. D.
10.如图,在中,,,垂直平分,交于点D,则周长的最小值是( )
A.12 B.6 C.7 D.8
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.已知2×4x+1×16=223,则x的值为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如图,把长方形沿EF折叠,使D、C分别落在D′、C′的位置,若∠EFB=65°,则∠D′EF= °.
15.已知(x+y)2=49,(x﹣y)2=25,则xy= .
16.若(2x﹣1)(4x+a)的结果中不含x的一次项,则实数a的值为 .
第II卷
北师大版2024—2025学年七年级下册数学期末素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
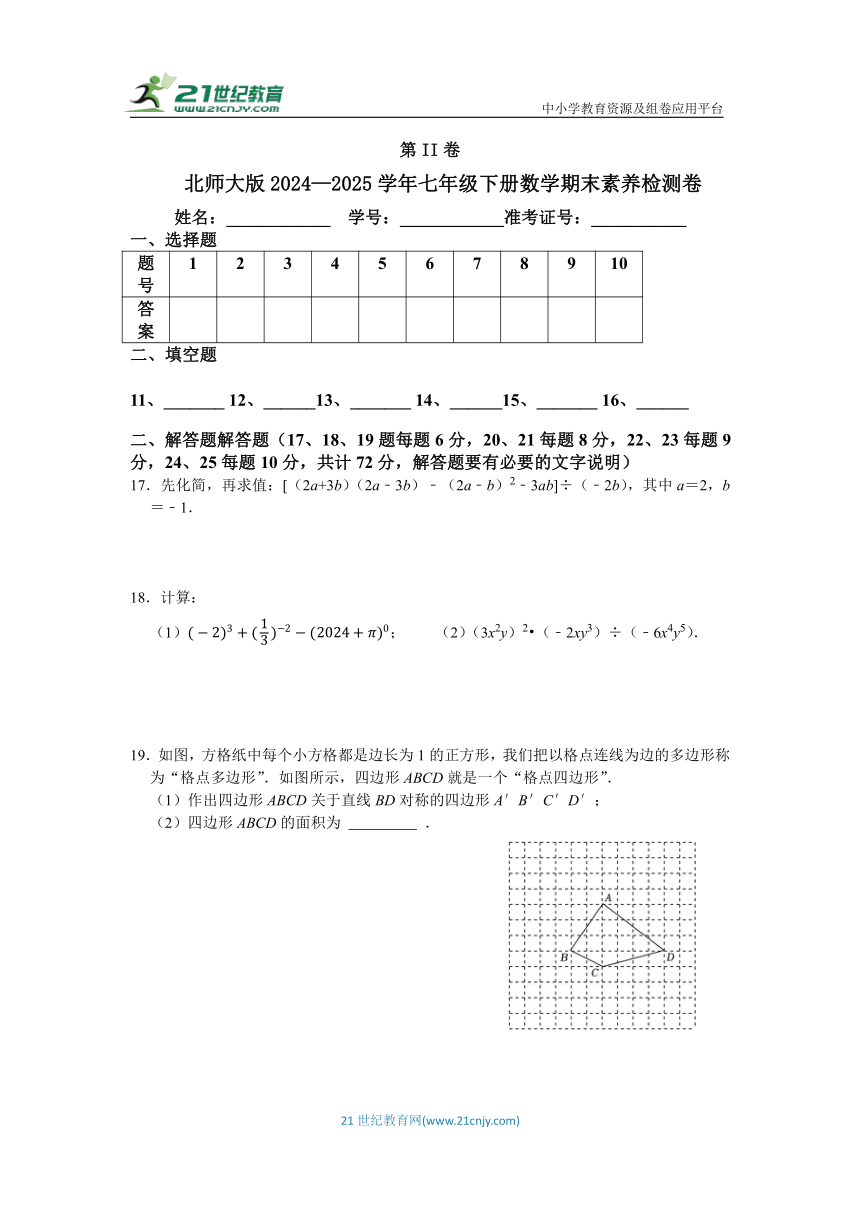
17.先化简,再求值:[(2a+3b)(2a﹣3b)﹣(2a﹣b)2﹣3ab]÷(﹣2b),其中a=2,b=﹣1.
18.计算:
(1); (2)(3x2y)2 (﹣2xy3)÷(﹣6x4y5).
19.如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图所示,四边形ABCD就是一个“格点四边形”.
(1)作出四边形ABCD关于直线BD对称的四边形A′B′C′D′;
(2)四边形ABCD的面积为 .
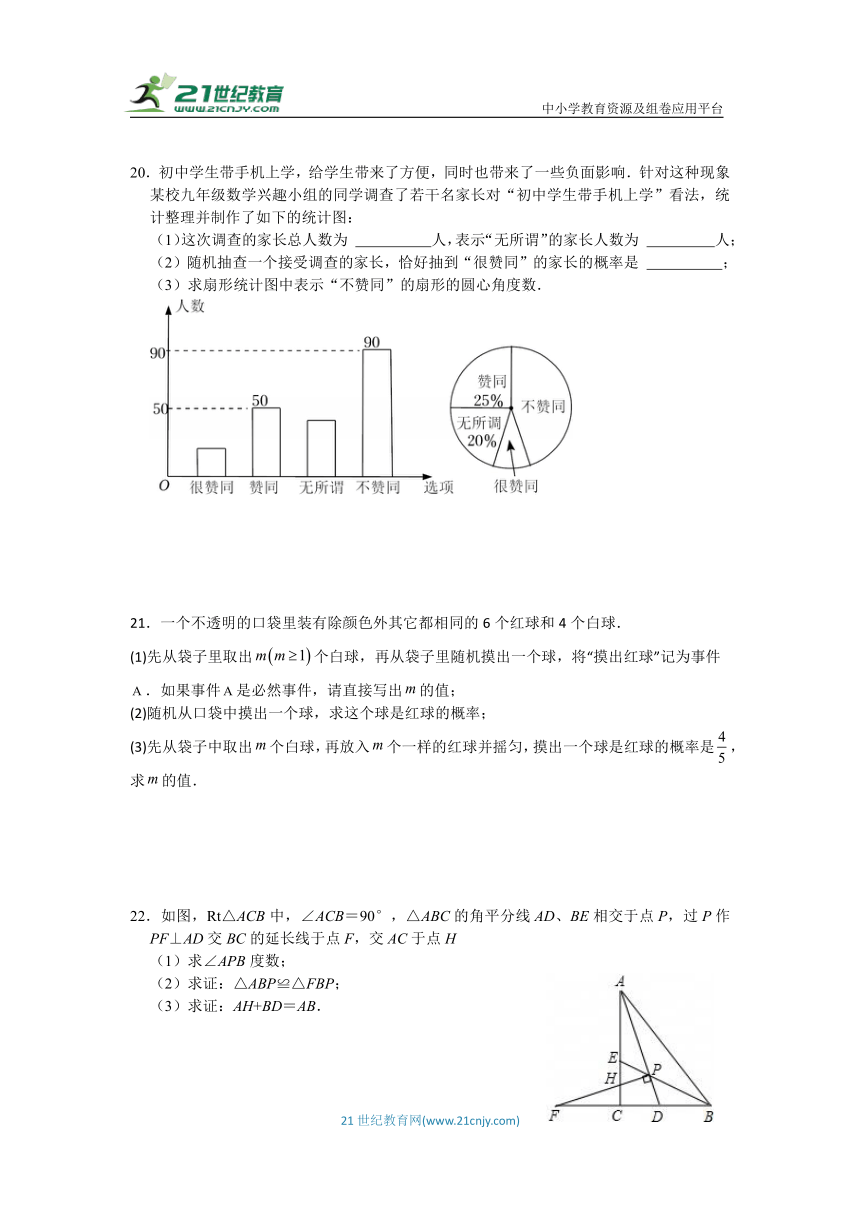
20.初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总人数为 人,表示“无所谓”的家长人数为 人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是 ;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
21.一个不透明的口袋里装有除颜色外其它都相同的6个红球和4个白球.
(1)先从袋子里取出个白球,再从袋子里随机摸出一个球,将“摸出红球”记为事件.如果事件是必然事件,请直接写出的值;
(2)随机从口袋中摸出一个球,求这个球是红球的概率;
(3)先从袋子中取出个白球,再放入个一样的红球并摇匀,摸出一个球是红球的概率是,求的值.
22.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
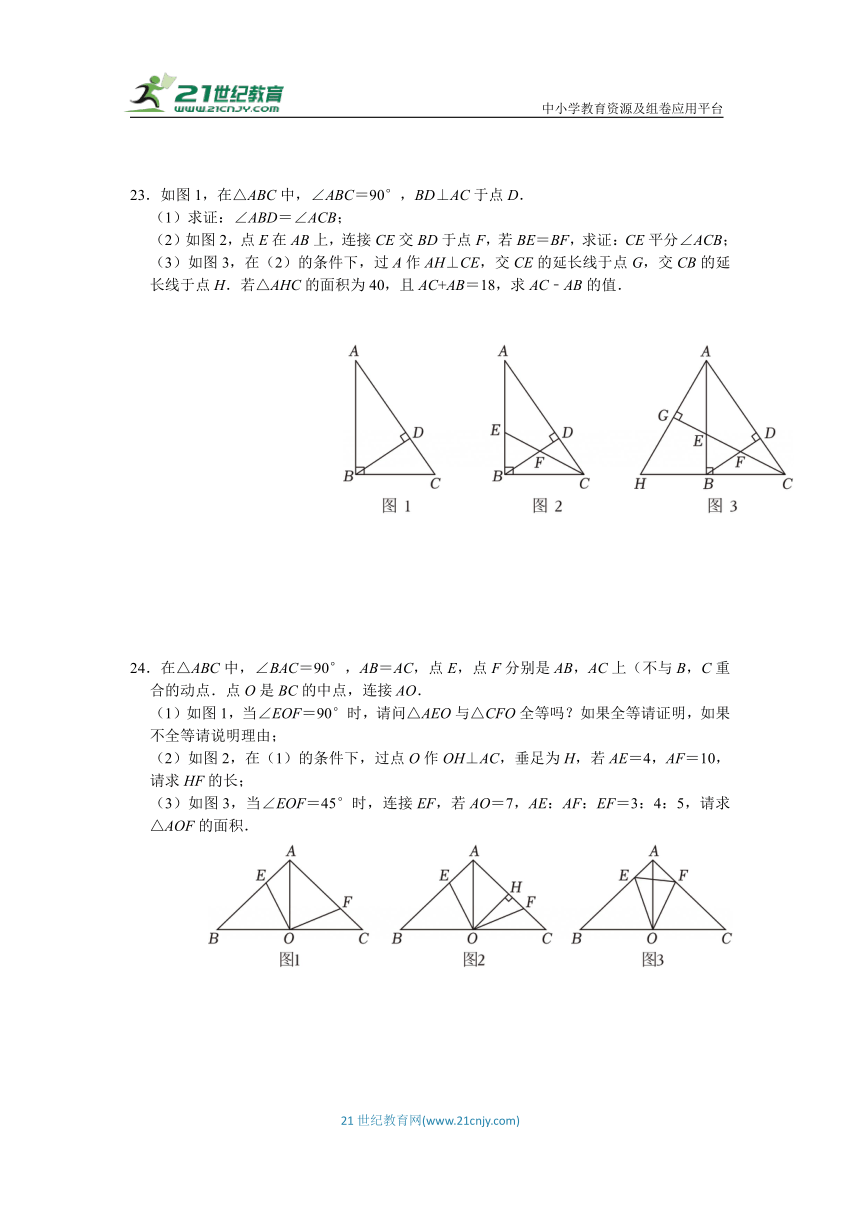
23.如图1,在△ABC中,∠ABC=90°,BD⊥AC于点D.
(1)求证:∠ABD=∠ACB;
(2)如图2,点E在AB上,连接CE交BD于点F,若BE=BF,求证:CE平分∠ACB;
(3)如图3,在(2)的条件下,过A作AH⊥CE,交CE的延长线于点G,交CB的延长线于点H.若△AHC的面积为40,且AC+AB=18,求AC﹣AB的值.
24.在△ABC中,∠BAC=90°,AB=AC,点E,点F分别是AB,AC上(不与B,C重合的动点.点O是BC的中点,连接AO.
(1)如图1,当∠EOF=90°时,请问△AEO与△CFO全等吗?如果全等请证明,如果不全等请说明理由;
(2)如图2,在(1)的条件下,过点O作OH⊥AC,垂足为H,若AE=4,AF=10,请求HF的长;
(3)如图3,当∠EOF=45°时,连接EF,若AO=7,AE:AF:EF=3:4:5,请求△AOF的面积.
25.如图1,有边长分别为m,n的两个正方形和两个长宽分别为n,m的长方形,将它们拼成如图2所示的大正方形ABCD.四边形AHOE,HDGO,OGCF,EOFB的面积分别为S1,S2,S3,S4.
(1)用两种方法表示图2的面积,可以得到一个关于m,n的等式为 ;
(2)在图2中,若S1=3,S2=9,则m+n= ;若m+n=12,S1=35,则S2+S4= ;
(3)如图3,连接AF交EO于点N,连接GF.若△FGN与△AEN的面积之差为18,求m的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B C D D C B B C
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:∵2×4x+1×16
=2×22x+2×24
=22x+7
=223,
∴2x+7=23,
∴x=8.
故答案为:8.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
14.【解答】解:∵AD∥BC,
∴∠EFB=∠FED=65°,
由折叠的性质知,∠D′EF=∠FED=65°,
故答案为:65.
15.【解答】解:∵(x+y)2=49,
∴x2+2xy+y2=49①,
∵(x﹣y)2=25,
∴x2﹣2xy+y2=25②,
①﹣②,得4xy=24,
∴xy=6,
故答案为:6.
16.【解答】解:(2x﹣1)(4x+a)=8x2+2ax﹣4x﹣a=8x2+(2a﹣4)x﹣a,
∵结果不含x的一次项,
∴2a﹣4=0,
解得:a=2;
故答案为:2.
三、解答题
17.【解答】解:原式=[4a2﹣9b2﹣(4a2﹣4ab+b2)﹣3ab]÷(﹣2b)
=(4a2﹣9b2﹣4a2+4ab﹣b2﹣3ab)÷(﹣2b)
=(﹣10b2+ab)÷(﹣2b)
=5ba,
当a=2,b=﹣1时,
原式=5×(﹣1)2
=﹣5﹣1
=﹣6.
18.【解答】解:(1)原式=﹣8+9﹣1
=0;
(2)原式=9x4y2 (﹣2xy3)÷(﹣6x4y5)
=﹣18x5y5÷(﹣6x4y5)
=3x.
19.【解答】解:(1)如图所示,四边形A′B′C′D′即为所求;
(2),
故答案为:12.
20.【解答】解:(1)这次调查的家长总人数为:50÷25%=200(人),
表示“无所谓”的家长人数为:200×20%=40(人).
故答案为:200,40;
(2)“很赞同”的家长人数为:200﹣90﹣50﹣40=20(人),
抽到“很赞同”的家长的概率是20÷200.
故答案为:;
(3)“不赞同”的扇形的圆心角度数为:360°=162°.
21.【解答】(1)解:如果事件是必然事件,则袋子里全是红球,
;
(2)解:随机从口袋中摸出一个球,这个球是红球的概率为;
(3)解:根据题意得:,
解得:.
22.【解答】解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA(∠ABC+∠BAC)=45°,
∴∠APB=180°﹣45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
23.【解答】(1)证明:∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵BD⊥AC,
∴∠ACB+∠CBD=90°,
∴∠ABD=∠ACB;
(2)证明:同(1)的方法可得:∠A=∠CBD,
∵BE=BF,
∴∠BEF=∠BFE,
∵∠BEF=∠A+∠ACE,∠BFE=∠CBD+∠BCE,
∴∠ACE=∠BCE,
∴CE平分∠ACB;
(3)解:在△ACG和△HCG中,
,
∴△ACG≌△HCG(ASA),
∴AC=CH,
∵△AHC的面积为40,
∴AB HC=40,
∴2AB HC=160,
∴2AB AC=160,
∵AC+AB=18,
∴(AC+AB)2=324,
∴AC2+2AB AC+AB2=324,
∴AC2﹣2AB AC+AB2=4,
∴(AC﹣AB)2=4,
∴AC﹣AB=2.
24.【解答】解:(1)△AEO≌△CFO,
理由:∵点O是BC的中点,
∴OB=OC,
∵AB=AC,
∴AD⊥BC,
∴∠AOB=∠AOD=90°,
∴∠AOF+∠COF=90°,
∵∠EOF=90°,
∴∠AOE+∠AOF=90°,
∴∠AOE=∠COF,
在Rt△ABC中,AB=AC,∠BAC=90°,AD⊥BC,
∴OC=OA,∠C=∠B=45°,,
∴∠OAC=∠C,
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA);
(2)由(1)知,∠AOC=90°,OA=OC,
∵OH⊥AC,
∴,
由(1)知,△AOE≌△COF,
∴CF=AE,
∵AE=4,
∴CF=4,
∵AF=10,
∴AC=AF+CF=14,
∴4=3;
(3)∵AE:AF:EF=3:4:5,设AE=3x,AF=4x,EF=5x,如图,过点O作OG⊥OE交AC于G,过点O作OM⊥AC于点M,
∴∠EOG=90°,
∵∠EOF=45°,
∴∠FOG=∠EOG﹣∠EOF=45°=∠EOF,
同(1)的方法得,△AOE≌△COG(ASA),
∴AE=CG=3x,OE=OG,
∵OF=OF,
∴△EOF≌△GOF(SAS),
∴EF=FG=5x,
同(1)的方法得,∠AOC=90°,OA=OC,
∴,
∴AC=AF+FG+CG=4x+5x+3x=12x,
∴,
过点O作OM⊥AC于M,则,
∴.
24.【解答】解:(1)∵S1=S3=mn,S2=n2,S4=m2,AD=AB=m+n,
∴(m+n)2=mn+n2+mn+m2=m2+2mn+n2,
故答案为:(m+n)2=m2+2mn+n2;
(2)若S1=3,S2=9,则mn=3,n2=9,
∴n=3,m=1,
∴m+n=1+3=4;
若m+n=12,S1=35,
∴m+n=12,mn=35,
∴m=5,n=7,
∴S2=72=49,S4=52=25,
∴S2+S4=49+25=74;
故答案为:4;74;
(3)∵△FGN与△AEN的面积之差为18,
∴S△FGN﹣S△AEN=18,
∴(S△FGN+S梯形BENF)﹣(S△AEN+S梯形BENF)=18,
即S梯形BEGF﹣S△ABF=18,
∴m(2m+n)m(m+n)=18,
∴m[(2m+n)﹣(m+n)]=18,
∴m2=36,
∴m=6或m=﹣6(负值舍去),
故m的值为6.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下册数学期末素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
选择题(每题只有一个正确选项,每小题3分,满分30分)
1.正方形的周长C与其边长a的函数关系式为,其中常量是( )
A.4 B.a C.C D.
2.中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅图案分别代表“立春、立夏、芒种、大雪”,其中不是轴对称图形的是( )
A. B. C. D.
3.经过近60年的发展,我国已建成目前世界上技术手段最为完 备的国家授时系统,授时精度从开始的毫秒级(千分之一秒)到了如今的百皮秒级(百亿分之一秒),提高了7个数量级,处于世界领先水平.已知1秒毫秒,1毫秒皮秒,则10秒等于( )
A.皮秒 B.皮秒 C.皮秒 D.皮秒
4.若的乘积中不含项,则常数m的值为( )
A.5 B. C. D.
5.下列各式中,不能用平方差公式计算的是( )
A. B.
C. D.
6.如图,有三张边长分别为,,的正方形纸片,,,将三张纸片按图1,图2两种不同方式放置于同一长方形中.记图1中阴影部分周长为,面积为;图2中阴影部分周长为,面积为,若,则与满足的关系为( )
A. B. C. D.
7.下列说法不正确的是( )
A.为了了解春节联欢晚会的收视率,选择抽样调查
B.为了审核书稿中的错别字,选择全面调查
C.“经过交通信号灯的路口,遇到红灯”是必然事件
D.“射击运动员射击一次命中靶心”是随机事件
8.下面每组中的三条线段,能围成三角形的是( )
A. B. C. D.
9.如图,已知直线,平分,若,则的度数是( )
A. B. C. D.
10.如图,在中,,,垂直平分,交于点D,则周长的最小值是( )
A.12 B.6 C.7 D.8
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.已知2×4x+1×16=223,则x的值为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如图,把长方形沿EF折叠,使D、C分别落在D′、C′的位置,若∠EFB=65°,则∠D′EF= °.
15.已知(x+y)2=49,(x﹣y)2=25,则xy= .
16.若(2x﹣1)(4x+a)的结果中不含x的一次项,则实数a的值为 .
第II卷
北师大版2024—2025学年七年级下册数学期末素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:[(2a+3b)(2a﹣3b)﹣(2a﹣b)2﹣3ab]÷(﹣2b),其中a=2,b=﹣1.
18.计算:
(1); (2)(3x2y)2 (﹣2xy3)÷(﹣6x4y5).
19.如图,方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.如图所示,四边形ABCD就是一个“格点四边形”.
(1)作出四边形ABCD关于直线BD对称的四边形A′B′C′D′;
(2)四边形ABCD的面积为 .
20.初中学生带手机上学,给学生带来了方便,同时也带来了一些负面影响.针对这种现象某校九年级数学兴趣小组的同学调查了若干名家长对“初中学生带手机上学”看法,统计整理并制作了如下的统计图:
(1)这次调查的家长总人数为 人,表示“无所谓”的家长人数为 人;
(2)随机抽查一个接受调查的家长,恰好抽到“很赞同”的家长的概率是 ;
(3)求扇形统计图中表示“不赞同”的扇形的圆心角度数.
21.一个不透明的口袋里装有除颜色外其它都相同的6个红球和4个白球.
(1)先从袋子里取出个白球,再从袋子里随机摸出一个球,将“摸出红球”记为事件.如果事件是必然事件,请直接写出的值;
(2)随机从口袋中摸出一个球,求这个球是红球的概率;
(3)先从袋子中取出个白球,再放入个一样的红球并摇匀,摸出一个球是红球的概率是,求的值.
22.如图,Rt△ACB中,∠ACB=90°,△ABC的角平分线AD、BE相交于点P,过P作PF⊥AD交BC的延长线于点F,交AC于点H
(1)求∠APB度数;
(2)求证:△ABP≌△FBP;
(3)求证:AH+BD=AB.
23.如图1,在△ABC中,∠ABC=90°,BD⊥AC于点D.
(1)求证:∠ABD=∠ACB;
(2)如图2,点E在AB上,连接CE交BD于点F,若BE=BF,求证:CE平分∠ACB;
(3)如图3,在(2)的条件下,过A作AH⊥CE,交CE的延长线于点G,交CB的延长线于点H.若△AHC的面积为40,且AC+AB=18,求AC﹣AB的值.
24.在△ABC中,∠BAC=90°,AB=AC,点E,点F分别是AB,AC上(不与B,C重合的动点.点O是BC的中点,连接AO.
(1)如图1,当∠EOF=90°时,请问△AEO与△CFO全等吗?如果全等请证明,如果不全等请说明理由;
(2)如图2,在(1)的条件下,过点O作OH⊥AC,垂足为H,若AE=4,AF=10,请求HF的长;
(3)如图3,当∠EOF=45°时,连接EF,若AO=7,AE:AF:EF=3:4:5,请求△AOF的面积.
25.如图1,有边长分别为m,n的两个正方形和两个长宽分别为n,m的长方形,将它们拼成如图2所示的大正方形ABCD.四边形AHOE,HDGO,OGCF,EOFB的面积分别为S1,S2,S3,S4.
(1)用两种方法表示图2的面积,可以得到一个关于m,n的等式为 ;
(2)在图2中,若S1=3,S2=9,则m+n= ;若m+n=12,S1=35,则S2+S4= ;
(3)如图3,连接AF交EO于点N,连接GF.若△FGN与△AEN的面积之差为18,求m的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B C D D C B B C
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:∵2×4x+1×16
=2×22x+2×24
=22x+7
=223,
∴2x+7=23,
∴x=8.
故答案为:8.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
14.【解答】解:∵AD∥BC,
∴∠EFB=∠FED=65°,
由折叠的性质知,∠D′EF=∠FED=65°,
故答案为:65.
15.【解答】解:∵(x+y)2=49,
∴x2+2xy+y2=49①,
∵(x﹣y)2=25,
∴x2﹣2xy+y2=25②,
①﹣②,得4xy=24,
∴xy=6,
故答案为:6.
16.【解答】解:(2x﹣1)(4x+a)=8x2+2ax﹣4x﹣a=8x2+(2a﹣4)x﹣a,
∵结果不含x的一次项,
∴2a﹣4=0,
解得:a=2;
故答案为:2.
三、解答题
17.【解答】解:原式=[4a2﹣9b2﹣(4a2﹣4ab+b2)﹣3ab]÷(﹣2b)
=(4a2﹣9b2﹣4a2+4ab﹣b2﹣3ab)÷(﹣2b)
=(﹣10b2+ab)÷(﹣2b)
=5ba,
当a=2,b=﹣1时,
原式=5×(﹣1)2
=﹣5﹣1
=﹣6.
18.【解答】解:(1)原式=﹣8+9﹣1
=0;
(2)原式=9x4y2 (﹣2xy3)÷(﹣6x4y5)
=﹣18x5y5÷(﹣6x4y5)
=3x.
19.【解答】解:(1)如图所示,四边形A′B′C′D′即为所求;
(2),
故答案为:12.
20.【解答】解:(1)这次调查的家长总人数为:50÷25%=200(人),
表示“无所谓”的家长人数为:200×20%=40(人).
故答案为:200,40;
(2)“很赞同”的家长人数为:200﹣90﹣50﹣40=20(人),
抽到“很赞同”的家长的概率是20÷200.
故答案为:;
(3)“不赞同”的扇形的圆心角度数为:360°=162°.
21.【解答】(1)解:如果事件是必然事件,则袋子里全是红球,
;
(2)解:随机从口袋中摸出一个球,这个球是红球的概率为;
(3)解:根据题意得:,
解得:.
22.【解答】解:(1)∵AD平分∠BAC,BE平分∠ABC,
∴∠PAB+∠PBA(∠ABC+∠BAC)=45°,
∴∠APB=180°﹣45°=135°;
(2)∵∠APB=135°,
∴∠DPB=45°,
∵PF⊥AD,
∴∠BPF=135°,
在△ABP和△FBP中,
,
∴△ABP≌△FBP(ASA);
(3)∵△ABP≌△FBP,
∴∠F=∠BAD,AP=PF,AB=BF,
∵∠BAD=∠CAD,
∴∠F=∠CAD,
在△APH和△FPD中,
,
∴△APH≌△FPD(ASA),
∴AH=DF,
∵BF=DF+BD,
∴AB=AH+BD.
23.【解答】(1)证明:∵∠ABC=90°,
∴∠ABD+∠CBD=90°,
∵BD⊥AC,
∴∠ACB+∠CBD=90°,
∴∠ABD=∠ACB;
(2)证明:同(1)的方法可得:∠A=∠CBD,
∵BE=BF,
∴∠BEF=∠BFE,
∵∠BEF=∠A+∠ACE,∠BFE=∠CBD+∠BCE,
∴∠ACE=∠BCE,
∴CE平分∠ACB;
(3)解:在△ACG和△HCG中,
,
∴△ACG≌△HCG(ASA),
∴AC=CH,
∵△AHC的面积为40,
∴AB HC=40,
∴2AB HC=160,
∴2AB AC=160,
∵AC+AB=18,
∴(AC+AB)2=324,
∴AC2+2AB AC+AB2=324,
∴AC2﹣2AB AC+AB2=4,
∴(AC﹣AB)2=4,
∴AC﹣AB=2.
24.【解答】解:(1)△AEO≌△CFO,
理由:∵点O是BC的中点,
∴OB=OC,
∵AB=AC,
∴AD⊥BC,
∴∠AOB=∠AOD=90°,
∴∠AOF+∠COF=90°,
∵∠EOF=90°,
∴∠AOE+∠AOF=90°,
∴∠AOE=∠COF,
在Rt△ABC中,AB=AC,∠BAC=90°,AD⊥BC,
∴OC=OA,∠C=∠B=45°,,
∴∠OAC=∠C,
在△AEO和△CFO中,
∴△AEO≌△CFO(ASA);
(2)由(1)知,∠AOC=90°,OA=OC,
∵OH⊥AC,
∴,
由(1)知,△AOE≌△COF,
∴CF=AE,
∵AE=4,
∴CF=4,
∵AF=10,
∴AC=AF+CF=14,
∴4=3;
(3)∵AE:AF:EF=3:4:5,设AE=3x,AF=4x,EF=5x,如图,过点O作OG⊥OE交AC于G,过点O作OM⊥AC于点M,
∴∠EOG=90°,
∵∠EOF=45°,
∴∠FOG=∠EOG﹣∠EOF=45°=∠EOF,
同(1)的方法得,△AOE≌△COG(ASA),
∴AE=CG=3x,OE=OG,
∵OF=OF,
∴△EOF≌△GOF(SAS),
∴EF=FG=5x,
同(1)的方法得,∠AOC=90°,OA=OC,
∴,
∴AC=AF+FG+CG=4x+5x+3x=12x,
∴,
过点O作OM⊥AC于M,则,
∴.
24.【解答】解:(1)∵S1=S3=mn,S2=n2,S4=m2,AD=AB=m+n,
∴(m+n)2=mn+n2+mn+m2=m2+2mn+n2,
故答案为:(m+n)2=m2+2mn+n2;
(2)若S1=3,S2=9,则mn=3,n2=9,
∴n=3,m=1,
∴m+n=1+3=4;
若m+n=12,S1=35,
∴m+n=12,mn=35,
∴m=5,n=7,
∴S2=72=49,S4=52=25,
∴S2+S4=49+25=74;
故答案为:4;74;
(3)∵△FGN与△AEN的面积之差为18,
∴S△FGN﹣S△AEN=18,
∴(S△FGN+S梯形BENF)﹣(S△AEN+S梯形BENF)=18,
即S梯形BEGF﹣S△ABF=18,
∴m(2m+n)m(m+n)=18,
∴m[(2m+n)﹣(m+n)]=18,
∴m2=36,
∴m=6或m=﹣6(负值舍去),
故m的值为6.
21世纪教育网(www.21cnjy.com)
同课章节目录
