北师大版2024—2025学年八年级下学期数学期末复习押题卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年八年级下学期数学期末复习押题卷(含答案) | 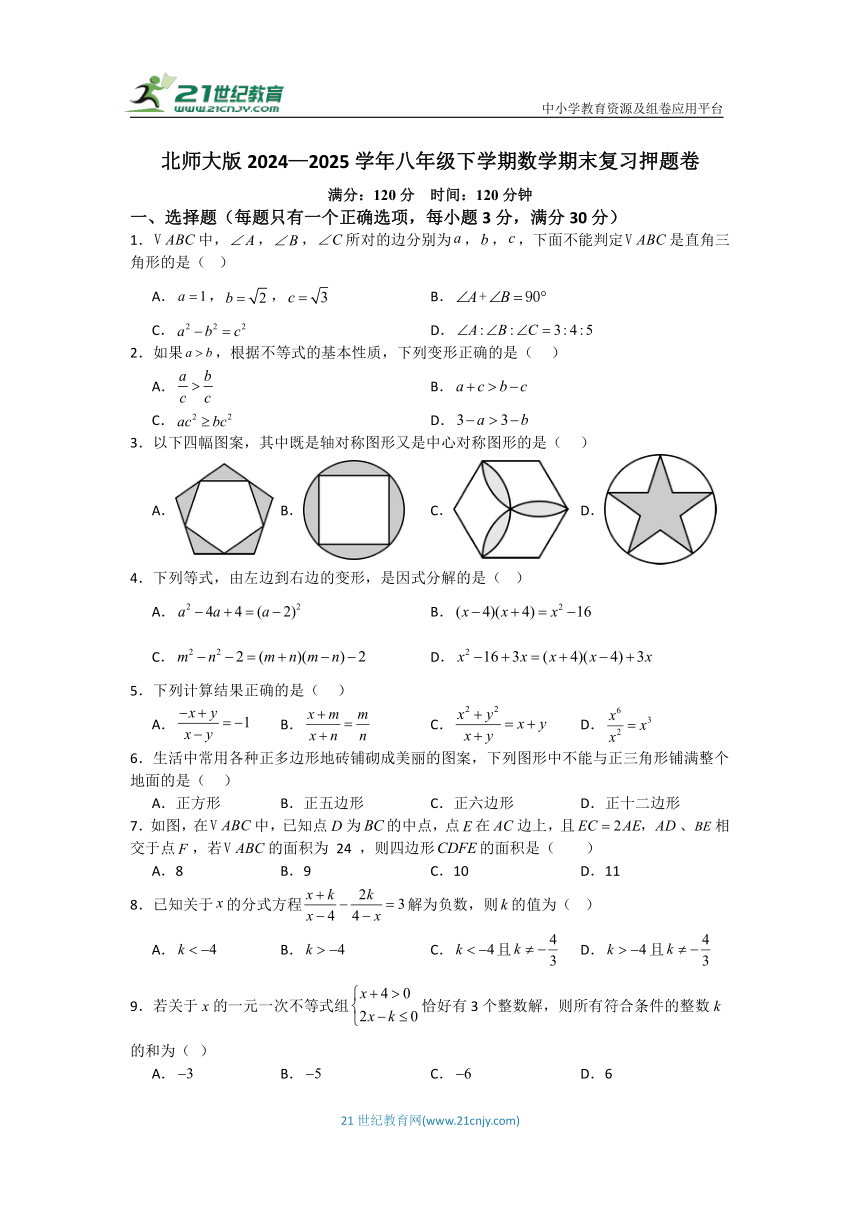 | |
| 格式 | docx | ||
| 文件大小 | 889.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 12:55:04 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年八年级下学期数学期末复习押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.中,,,所对的边分别为,,,下面不能判定是直角三角形的是( )
A.,, B.
C. D.
2.如果,根据不等式的基本性质,下列变形正确的是( )
A. B.
C. D.
3.以下四幅图案,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列等式,由左边到右边的变形,是因式分解的是( )
A. B.
C. D.
5.下列计算结果正确的是( )
A. B. C. D.
6.生活中常用各种正多边形地砖铺砌成美丽的图案,下列图形中不能与正三角形铺满整个地面的是( )
A.正方形 B.正五边形 C.正六边形 D.正十二边形
7.如图,在中,已知点D为的中点,点在边上,且、相交于点,若的面积为 24 ,则四边形的面积是( )
A.8 B.9 C.10 D.11
8.已知关于的分式方程解为负数,则的值为( )
A. B. C.且 D.且
9.若关于x的一元一次不等式组恰好有3个整数解,则所有符合条件的整数k的和为( )
A. B. C. D.6
10.如图,在平面直角坐标系中,已知一次函数的图像与轴交于点,与轴交于点,,是该函数图像上的两个动点,且,连结、,则周长的最小值为( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.若不等式(m﹣2024)x>m﹣2024两边同时除以(m﹣2024),得x<1,则m的取值范围是 .
12.若点P(a﹣2,5)在第二象限,且a为正整数,则a的值为 .
13.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= .
14.如图,在△ABC中,AB=8,点D、E分别是边AB、AC的中点,点F是线段DE上的一点且EF=2,连接AF、BF,若∠AFB=90°,则线段BC的长为 .
15.若关于x的不等式组无解,则a的取值范围为 .
16.某种商品的进价为400元,出售时标价为500元,商店准备打折出售,但要保持利润率不低于10%,则至多可以打 折.
第II卷
北师大版2024—2025学年八年级下学期数学期末复习押题卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
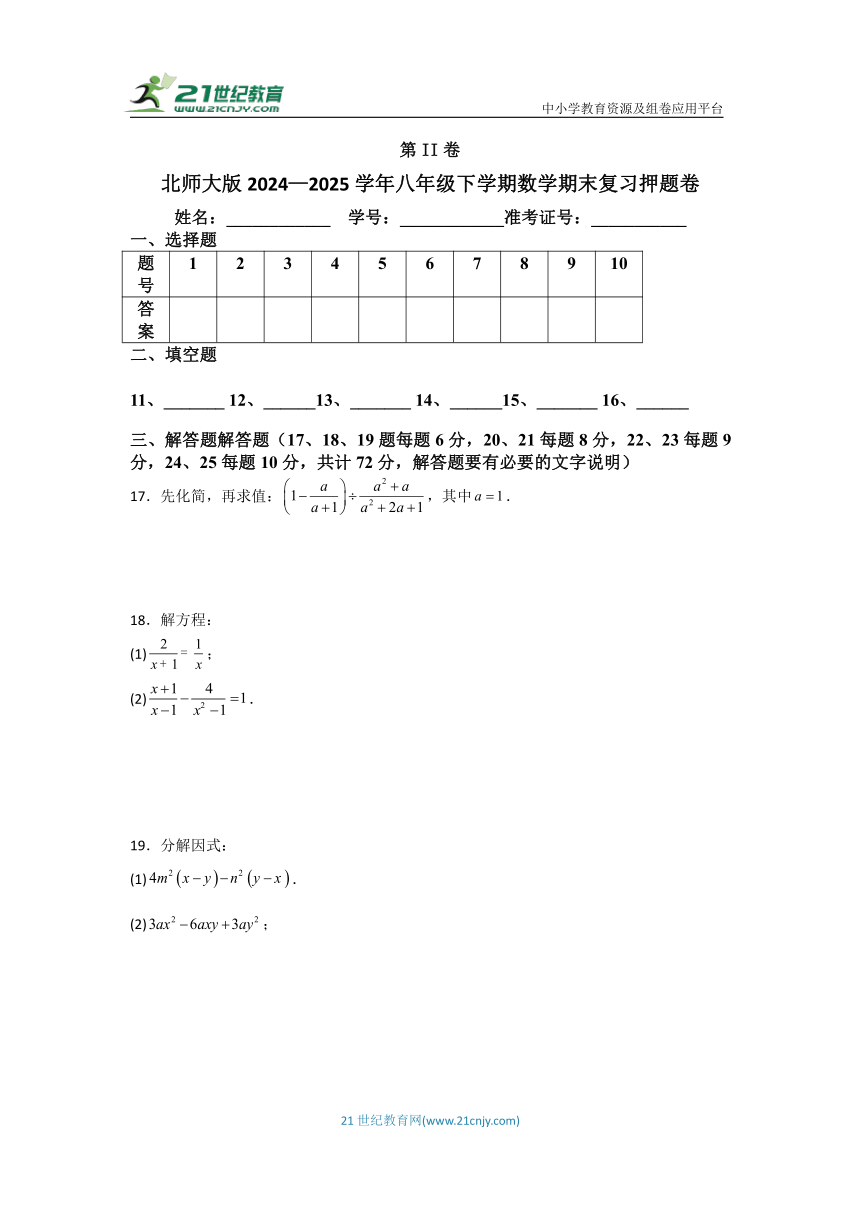
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中.
18.解方程:
(1);
(2).
19.分解因式:
(1).
(2);
20.(1)解不等式:;
(2)解不等式组:,利用数轴求不等式组的解集.
21.三角形在如图所示的平面直角坐标系中,将其平移得到三角形,若点的对应点的坐标为.
(1)在图中画出三角形;
(2)此次平移可以看作将三角形向 平移 个单位长度,再向 平移 个单位长度得到三角形;
(3)求三角形的面积.
22.习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲,乙两种农机具,已知1件乙种农机具比1件甲种农机具多0.5万元,用20万元购买甲种农机具的数量和用25万元购买乙种农机具的数量相同.
(1)求购买1件甲种农机具和1件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲,乙两种农机具共30件,且乙的件数不低于甲件数的一半.设购买甲种农机具m件,购买的总费用为W万元,求购买这批农机具最少要用多少万元?
23.已知中,为边上的中线,且,
(1)如图1,求证:;
(2)如图2,延长到点E,使得,连接,求证:;
(3)如图3,在(2)的条件下,连接,点F在上,点G在边下方,连接,且满足,,若, ,求长.
24.在中,,点是边上一点,连接.
(1)如图1,若,求的度数;
(2)如图2,若点是的中点,点是边上一点,且,求证:;
(3)如图3,若平分,点是上一动点,点是上一动点,连接,若的面积为10,,请直接写出的最小值.
25.新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“相依方程”,例如:方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“相依方程”.
(1)在方程①;②中,不等式组的“相依方程”是________;(填序号)
(2)若关于的方程是不等式组的“相依方程”,求的取值范围;
(3)若关于的方程是关于的不等式组的“相依方程”,且此时不等式组有个整数解,试求的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B A A B C A A C
二、填空题
11.【解答】解:由题意得:m﹣2024<0,
解得:m<2024,
故答案为:m<2024.
12.【解答】解:∵点P(a﹣2,5)在第二象限,
∴a﹣2<0,
解得a<2,
∵a为正整数,
∴a=1,
故答案为:1.
13.【解答】解:∵△ABC为等边三角形,BD为△ABC的高,
∴点D为AC的中点,AC=BC,
∵CE=CD=1,
∴AC=2CD=2,
∴BC=2,
∴BE=BC+CE=2+1=3,
故答案为:3.
14.【解答】解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DEBC,
∵∠AFB=90°,D是AB的中点,AB=8,
∴DFAB8=4,
∵EF=2.
∴DE=EF+DF=6.
∴BC=12,
故答案为:12.
15.【解答】解:∵关于x的不等式组无解,
∴a﹣1≥2,
∴a≥3,
故答案为:a≥3.
16.【解答】解:要保持利润率不低于10%,设可打x折.
则500400≥400×10%,
解得x≥8.8.
故答案为:8.8.
三、解答题
17.【解】解:
,
∵,
∴.
18【解】(1)解:
去分母得,
解得
检验:将代入
∴是原方程的解;
(2)解:
去分母得,
解得
检验:将代入
∴是原方程的增根
∴原方程无解.
19.【解】(1)解:
;
(2)解:
.
20.【解】解:()
∴;
(),
解不等式得,
解不等式得,
在数轴上表示解集如图,
∴不等式组解集为.
21.【解】(1)解:如图,三角形即为所求;
(2)解:此次平移可以看作将向右平移6个单位长度,再向下平移1个单位长度,得;
(3)解:.
22.【解】(1)解:设购买1件甲种农机具需要万元,则购买1件乙种农机具需要万元,
由题意,得:,
解得:,
经检验:是原方程的解且符合题意;
∴,
答:购买1件甲种农机具需要万元,购买1件乙种农机具需要万元;
(2)设购买甲种农机具m件,则购买乙种农机具件,
由题意,得:,
解得:,
∵,
∴随着的增大而减小,
∴当时,有最小值,最小值;
答:购买这批农机具最少要用65万元.
23.【解】(1)证明:∵,
∴,,
∵,
∴,即;
(2)证明:取的中点,连接,
∵,
∴设,则,
∴,
∵,点是的中点,
∴,
∴,
∴是等边三角形,
∴;
(3)解:取的中点M,连接,过点G作 交 的延长线于点N,
∵D 为的中点,
∴,
∵,
∴,
设,
∴,
∴,,
∵,
∴,
∴,
∴,
∵D为的中点,M为的中点,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,,
∵,,
∴,
∴,
∵点M是的中点,
∴,
∴,
∵,
∴,
由(2)知,
∵,
∴,
∴,
在中,,
∴,
在中,,
∴,
∴.
24.【解】(1)解:∵,
∴,
∵,
∴,
∵,
∴;
(2)证明:延长至点H,使得,交于点G,如图,
∵点是的中点,
∴,
∵,,
∴,
∴,,
设,
∵,
∴,,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
则;
(3)解:过点C作于点M,CM交BD于点,过点作于点,如图,
则,
∵平分,
∴,
当点P位于点,,此时,的最小值,
∵的面积为10,,
∴,解得.
25.【解】(1)解:方程①,
解得:,
②,
解得:,
不等式组,
解得:,
∵在范围内,不在范围内,
∴方程①是不等式组的“相依方程”,
故答案为:①;
(2)不等式组,
解得:,
解关于的方程,
解得:,
∵关于的方程是不等式组的“相依方程”,
∴,
解得:;
(3)解关于的方程,
解得:,
解关于的不等式组,
解不等式①,得:,
解不等式②,得:,
∴不等式组的解集为,
∵不等式组有个整数解,
令整数的值为,,,,,,,
则有:,,
∴,
∴且,
∴,
∴,
∴,
∴,
∵关于的方程是关于的不等式组的“相依方程”,
∴,
解得:,
∴的取值范围是.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年八年级下学期数学期末复习押题卷
满分:120分 时间:120分钟
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.中,,,所对的边分别为,,,下面不能判定是直角三角形的是( )
A.,, B.
C. D.
2.如果,根据不等式的基本性质,下列变形正确的是( )
A. B.
C. D.
3.以下四幅图案,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
4.下列等式,由左边到右边的变形,是因式分解的是( )
A. B.
C. D.
5.下列计算结果正确的是( )
A. B. C. D.
6.生活中常用各种正多边形地砖铺砌成美丽的图案,下列图形中不能与正三角形铺满整个地面的是( )
A.正方形 B.正五边形 C.正六边形 D.正十二边形
7.如图,在中,已知点D为的中点,点在边上,且、相交于点,若的面积为 24 ,则四边形的面积是( )
A.8 B.9 C.10 D.11
8.已知关于的分式方程解为负数,则的值为( )
A. B. C.且 D.且
9.若关于x的一元一次不等式组恰好有3个整数解,则所有符合条件的整数k的和为( )
A. B. C. D.6
10.如图,在平面直角坐标系中,已知一次函数的图像与轴交于点,与轴交于点,,是该函数图像上的两个动点,且,连结、,则周长的最小值为( )
A. B. C. D.
二、填空题(每小题3分,满分18分)
11.若不等式(m﹣2024)x>m﹣2024两边同时除以(m﹣2024),得x<1,则m的取值范围是 .
12.若点P(a﹣2,5)在第二象限,且a为正整数,则a的值为 .
13.已知△ABC为等边三角形,BD为△ABC的高,延长BC至E,使CE=CD=1,连接DE,则BE= .
14.如图,在△ABC中,AB=8,点D、E分别是边AB、AC的中点,点F是线段DE上的一点且EF=2,连接AF、BF,若∠AFB=90°,则线段BC的长为 .
15.若关于x的不等式组无解,则a的取值范围为 .
16.某种商品的进价为400元,出售时标价为500元,商店准备打折出售,但要保持利润率不低于10%,则至多可以打 折.
第II卷
北师大版2024—2025学年八年级下学期数学期末复习押题卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值:,其中.
18.解方程:
(1);
(2).
19.分解因式:
(1).
(2);
20.(1)解不等式:;
(2)解不等式组:,利用数轴求不等式组的解集.
21.三角形在如图所示的平面直角坐标系中,将其平移得到三角形,若点的对应点的坐标为.
(1)在图中画出三角形;
(2)此次平移可以看作将三角形向 平移 个单位长度,再向 平移 个单位长度得到三角形;
(3)求三角形的面积.
22.习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买甲,乙两种农机具,已知1件乙种农机具比1件甲种农机具多0.5万元,用20万元购买甲种农机具的数量和用25万元购买乙种农机具的数量相同.
(1)求购买1件甲种农机具和1件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲,乙两种农机具共30件,且乙的件数不低于甲件数的一半.设购买甲种农机具m件,购买的总费用为W万元,求购买这批农机具最少要用多少万元?
23.已知中,为边上的中线,且,
(1)如图1,求证:;
(2)如图2,延长到点E,使得,连接,求证:;
(3)如图3,在(2)的条件下,连接,点F在上,点G在边下方,连接,且满足,,若, ,求长.
24.在中,,点是边上一点,连接.
(1)如图1,若,求的度数;
(2)如图2,若点是的中点,点是边上一点,且,求证:;
(3)如图3,若平分,点是上一动点,点是上一动点,连接,若的面积为10,,请直接写出的最小值.
25.新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“相依方程”,例如:方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“相依方程”.
(1)在方程①;②中,不等式组的“相依方程”是________;(填序号)
(2)若关于的方程是不等式组的“相依方程”,求的取值范围;
(3)若关于的方程是关于的不等式组的“相依方程”,且此时不等式组有个整数解,试求的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B A A B C A A C
二、填空题
11.【解答】解:由题意得:m﹣2024<0,
解得:m<2024,
故答案为:m<2024.
12.【解答】解:∵点P(a﹣2,5)在第二象限,
∴a﹣2<0,
解得a<2,
∵a为正整数,
∴a=1,
故答案为:1.
13.【解答】解:∵△ABC为等边三角形,BD为△ABC的高,
∴点D为AC的中点,AC=BC,
∵CE=CD=1,
∴AC=2CD=2,
∴BC=2,
∴BE=BC+CE=2+1=3,
故答案为:3.
14.【解答】解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∴DEBC,
∵∠AFB=90°,D是AB的中点,AB=8,
∴DFAB8=4,
∵EF=2.
∴DE=EF+DF=6.
∴BC=12,
故答案为:12.
15.【解答】解:∵关于x的不等式组无解,
∴a﹣1≥2,
∴a≥3,
故答案为:a≥3.
16.【解答】解:要保持利润率不低于10%,设可打x折.
则500400≥400×10%,
解得x≥8.8.
故答案为:8.8.
三、解答题
17.【解】解:
,
∵,
∴.
18【解】(1)解:
去分母得,
解得
检验:将代入
∴是原方程的解;
(2)解:
去分母得,
解得
检验:将代入
∴是原方程的增根
∴原方程无解.
19.【解】(1)解:
;
(2)解:
.
20.【解】解:()
∴;
(),
解不等式得,
解不等式得,
在数轴上表示解集如图,
∴不等式组解集为.
21.【解】(1)解:如图,三角形即为所求;
(2)解:此次平移可以看作将向右平移6个单位长度,再向下平移1个单位长度,得;
(3)解:.
22.【解】(1)解:设购买1件甲种农机具需要万元,则购买1件乙种农机具需要万元,
由题意,得:,
解得:,
经检验:是原方程的解且符合题意;
∴,
答:购买1件甲种农机具需要万元,购买1件乙种农机具需要万元;
(2)设购买甲种农机具m件,则购买乙种农机具件,
由题意,得:,
解得:,
∵,
∴随着的增大而减小,
∴当时,有最小值,最小值;
答:购买这批农机具最少要用65万元.
23.【解】(1)证明:∵,
∴,,
∵,
∴,即;
(2)证明:取的中点,连接,
∵,
∴设,则,
∴,
∵,点是的中点,
∴,
∴,
∴是等边三角形,
∴;
(3)解:取的中点M,连接,过点G作 交 的延长线于点N,
∵D 为的中点,
∴,
∵,
∴,
设,
∴,
∴,,
∵,
∴,
∴,
∴,
∵D为的中点,M为的中点,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,,
∵,,
∴,
∴,
∵点M是的中点,
∴,
∴,
∵,
∴,
由(2)知,
∵,
∴,
∴,
在中,,
∴,
在中,,
∴,
∴.
24.【解】(1)解:∵,
∴,
∵,
∴,
∵,
∴;
(2)证明:延长至点H,使得,交于点G,如图,
∵点是的中点,
∴,
∵,,
∴,
∴,,
设,
∵,
∴,,,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
则;
(3)解:过点C作于点M,CM交BD于点,过点作于点,如图,
则,
∵平分,
∴,
当点P位于点,,此时,的最小值,
∵的面积为10,,
∴,解得.
25.【解】(1)解:方程①,
解得:,
②,
解得:,
不等式组,
解得:,
∵在范围内,不在范围内,
∴方程①是不等式组的“相依方程”,
故答案为:①;
(2)不等式组,
解得:,
解关于的方程,
解得:,
∵关于的方程是不等式组的“相依方程”,
∴,
解得:;
(3)解关于的方程,
解得:,
解关于的不等式组,
解不等式①,得:,
解不等式②,得:,
∴不等式组的解集为,
∵不等式组有个整数解,
令整数的值为,,,,,,,
则有:,,
∴,
∴且,
∴,
∴,
∴,
∴,
∵关于的方程是关于的不等式组的“相依方程”,
∴,
解得:,
∴的取值范围是.
21世纪教育网(www.21cnjy.com)
同课章节目录
