人教版2024—2025学年八年级下学期数学期末复习调研与押题训练(含答案)
文档属性
| 名称 | 人教版2024—2025学年八年级下学期数学期末复习调研与押题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 929.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 13:04:51 | ||
图片预览


文档简介
人教版2024—2025学年八年级下学期数学期末复习调研与押题训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若数据1,4,2,x,5的平均数是3,则中位数是( )
A.4 B.3 C.2 D.1
2.下列二次根式中是最简二次根式的是( )
A. B. C. D.
3.下列四组数中,不是勾股数的是( )
A.,, B.,,
C.,, D.,,
4.如图,在矩形中,对角线,相交于点,若要使矩形成为正方形,添加的条件不正确的是( )
A. B. C. D.
5.若一次函数的图象经过第一、三、四象限,则( )
A. B. C. D.
6.估计的值应在( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
7.的两边,满足,则是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.等腰直角三角形
8.如图,菱形中,,,则菱形的周长为( )
A. B. C. D.
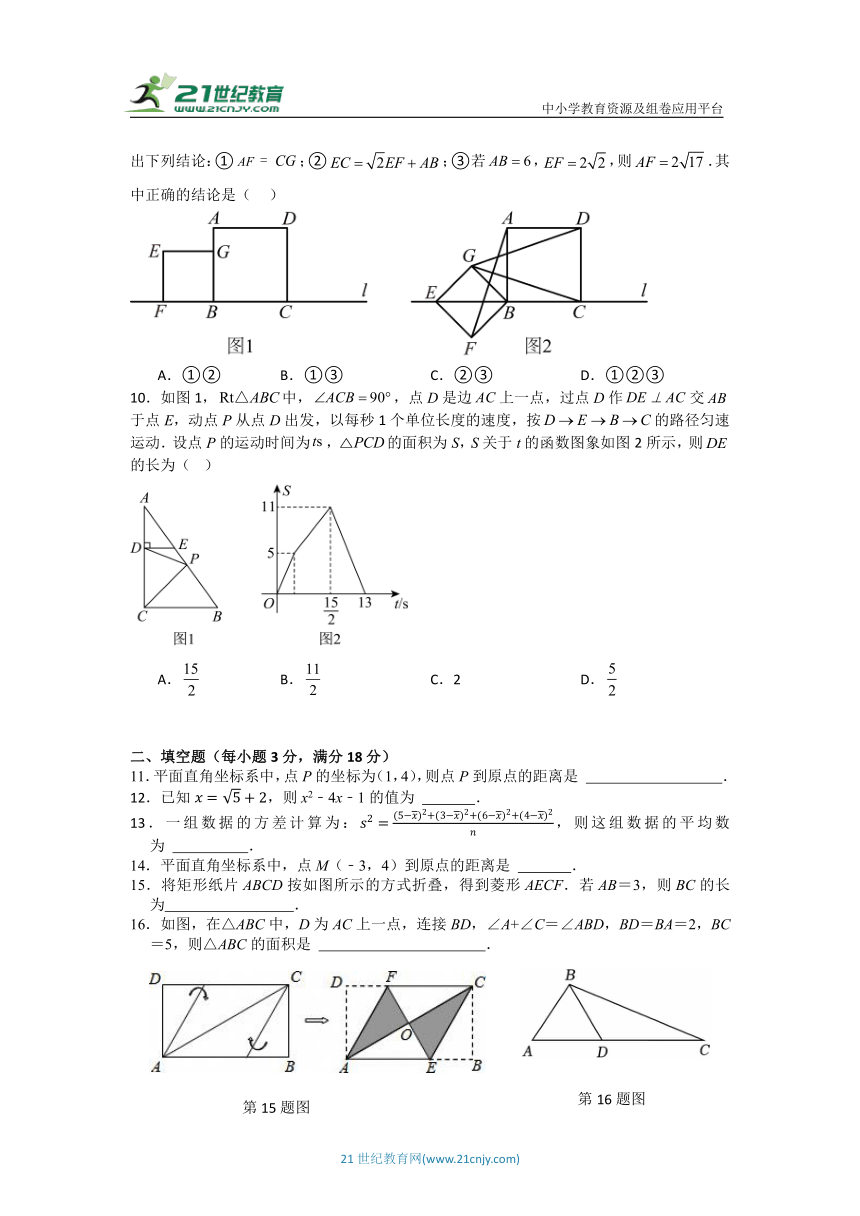
9.如图1,四边形、均为正方形,且点,,在同一直线上,将正方形绕点逆时针旋转,如图2,点,,在同一直线点,连接,,.给出下列结论:①;②;③若,,则.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
10.如图1,中,,点D是边上一点,过点D作交于点E,动点P从点D出发,以每秒1个单位长度的速度,按的路径匀速运动.设点P的运动时间为,的面积为S,S关于t的函数图象如图2所示,则的长为( )
A. B. C.2 D.
二、填空题(每小题3分,满分18分)
11.平面直角坐标系中,点P的坐标为(1,4),则点P到原点的距离是 .
12.已知,则x2﹣4x﹣1的值为 .
13.一组数据的方差计算为:,则这组数据的平均数为 .
14.平面直角坐标系中,点M(﹣3,4)到原点的距离是 .
15.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 .
16.如图,在△ABC中,D为AC上一点,连接BD,∠A+∠C=∠ABD,BD=BA=2,BC=5,则△ABC的面积是 .
人教版2024—2025学年八年级下学期数学期末复习调研与押题训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
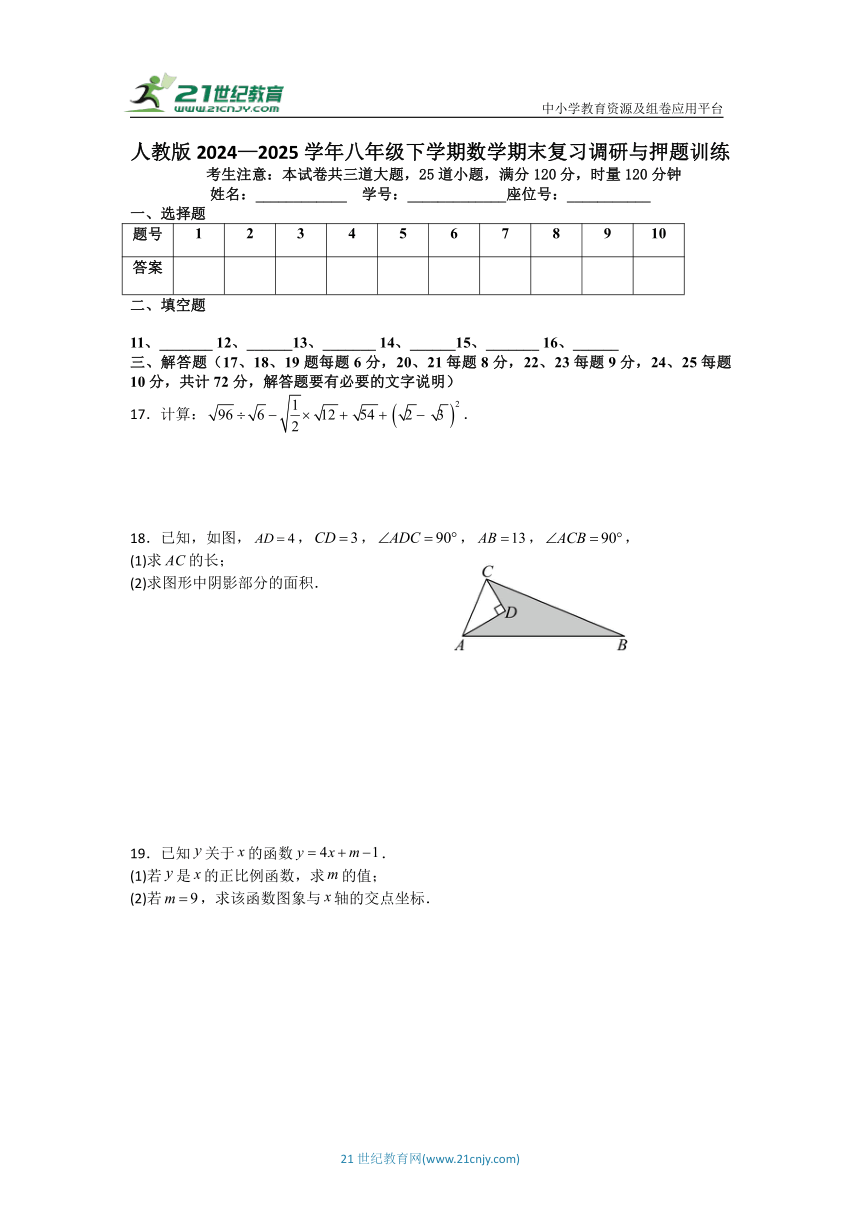
17.计算:.
18.已知,如图,,,,,,
(1)求的长;
(2)求图形中阴影部分的面积.
19.已知关于的函数.
(1)若是的正比例函数,求的值;
(2)若,求该函数图象与轴的交点坐标.
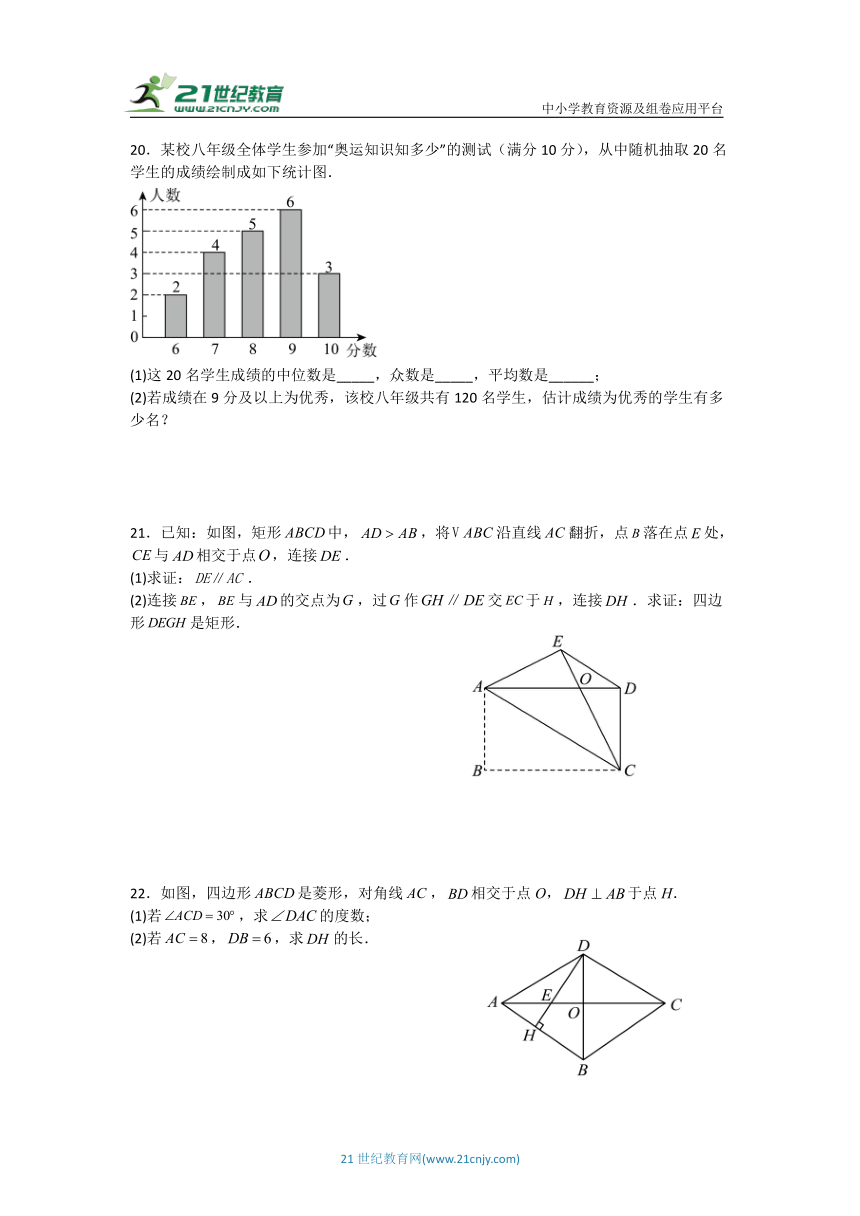
20.某校八年级全体学生参加“奥运知识知多少”的测试(满分10分),从中随机抽取20名学生的成绩绘制成如下统计图.
(1)这20名学生成绩的中位数是_____,众数是_____,平均数是______;
(2)若成绩在9分及以上为优秀,该校八年级共有120名学生,估计成绩为优秀的学生有多少名?
21.已知:如图,矩形中,,将沿直线翻折,点落在点处,与相交于点,连接.
(1)求证:.
(2)连接,与的交点为,过作交于,连接.求证:四边形是矩形.
22.如图,四边形是菱形,对角线,相交于点O,于点H.
(1)若,求的度数;
(2)若,,求的长.
23.随着deepseek的AI技术开发,更大激活智能机器人应用市场,为了更方便的服务广大读者,某图书馆准备引进智能机器人服务读者,购进甲、乙两种型号的机器人,已知甲种型号的单价比乙种型号的机器人多3万元,经过调研发现130万购买的甲中型号机器人和100万购买的乙种型号的机器人数量一样.
(1)求甲乙两种型号的机器人的单价是多少万元?
(2)图书馆经过统筹安排,准备用不低于114万的资金购进甲、乙两种型号的机器人共10套(两种型号均有),则有几种购买方案,购买乙种智能机器人多少套,所花资金最少?
24.如图1,在平面直角坐标系中,坐标原点为O,直线交x轴于点A,点B的坐标为,点C的坐标为.
(1)求直线的解析式和点A的坐标;
(2)以点C为直角顶点作,射线交x轴的正半轴于点E,射线交y轴的负半轴于点F.当绕着点C旋转时,的值是否发生变化,若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M是x轴上的一个动点,点P是坐标平面内一点.若B、C、M、P四点能构成菱形,求出满足条件的所有点P的坐标。
25.如图,在平面直角坐标系中,满足,过点分别作轴于点,轴于点.
(1)______,______.
(2)如图1,点,分别在线段,上(不与端点重合),,连接,,以,为边向右侧作.若,,则是什么特殊四边形?请说明理由.
(3)如图2,过作,交轴正半轴于点,若,求点的坐标.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D A B D D D D
二、填空题
11.【解答】解:由点P的坐标为(1,4),
则点P到原点的距离.
故答案为:.
12.【解答】解:∵,
∴x2﹣4x﹣1
=(x2﹣4x+4)﹣1﹣4
=(x﹣2)2﹣5
=(2﹣2)2﹣5
=()2﹣5
=5﹣5
=0.
故答案为:0.
13.【解答】解:由题意可知这组数据为5、3、6、4,
∴平均数为:(5+3+4+6)÷4=4.5.
故答案为:4.5.
14.【解答】解:作MA⊥x轴于A,则MA=4,OA=3.
则根据勾股定理,得OM=5.
故答案为5.
15.【解答】解:∵AECF为菱形,
∴∠FCO=∠ECO,
由折叠的性质可知,∠ECO=∠BCE,
又∠FCO+∠ECO+∠BCE=90°,
∴∠FCO=∠ECO=∠BCE=30°,
在Rt△EBC中,EC=2EB,
又EC=AE,
AB=AE+EB=3,
∴EB=1,EC=2,
∴Rt△BCE中,BCBE,
故答案为:.
16.【解答】解:延长CB,作AE⊥CB于点E,
∴∠EBA=∠BAC+∠C,
∵∠BAC+∠C=∠ABD,
∴∠EBA=∠ABD,
作AF⊥BD于点F,
∴AE=AF,
作BH⊥AD,
∵S△ABC BC AEAE,S△ABD BD AF=AF,
∴S△ABC:S△ABD=2:5,
∴AD:AC=2:5,
设AD=2x,
∴AC=5x,DC=3x,
∵BA=BD,
∴AH=DH=x,
∴HC=4x,
∴22﹣x2=52﹣(4x)2,
∴x,
∵BH2=22﹣()2,
∴BH,
∴S△ABC5.
故答案为:.
三、解答题
17.【解】解:原式
.
18.【解】(1)解:在中,;
(2)解:在中,,
.
∵,
.
19.【解】(1)解: 关于的函数是的正比例函数,
,解得.
(2)解:当时,该函数的表达式为,
令,得,解得:,
当时,函数图象与轴的交点坐标为.
20.【解】(1)解:由题意知,中位数是第10,11位数的平均数,即,
众数是9,
平均数为,
故答案为:8,9,;
(2)解:由题意知,(名),
答:估计该校120名学生中,成绩为优秀的学生有54名.
21.【解】(1)证明:矩形,
∴,.
∴,
∵沿直线翻折
.
.
,
∴.
∵,
∴,
∴.
.
.
在中,.
在中,.
又,
,
.
.
(2)证明:如图:
沿直线翻折,
.
,
,
,
,,
,
∴.
.
又.
.
,
,.
又,
.
,
∴四边形是平行四边形.
平行四边形是矩形.
22.【解】(1)解:∵四边形是菱形,
∴
∴;
(2)解:∵四边形是菱形
∴,,
∴在中,
∵,
∴,
∴.
23.【解】(1)解:设甲种型号的机器人的单价是x万元,则乙种型号的机器人的单价是万元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
∴(万元).
答:甲种型号的机器人的单价是13万元,乙种型号的机器人的单价是10万元;
(2)解:设购买乙种智能机器人m套,则购买甲种智能机器人套,
根据题意得:,
解得:,
又∵m,均为正整数,
∴m可以为1,2,3,4,5,
∴有5种购买方案.
设购买甲、乙两种型号的机器人共花费w万元,则,
即,
∵,
∴w随m的增大而减小,
∴当时,w取得最小值.
答:有5种购买方案,购买乙种智能机器人5套,所花资金最少.
24.【解】(1)解:设直线的解析式为:,
点,点在直线上,
,
解得,
直线的解析式为:;
把代入得:,
解得:,
∴;
(2)解:不变,理由如下:
过点C分别作x轴、y轴的垂线,垂足分别为M、N,如图,
则,
又,
,
,
,
,
,
,
,
在和中,
,
,
,
故的值不发生变化,值为6;
(3)解:设点M的坐标为,点P的坐标为,
∵,,
∴,
,
,
①为对角线时,
则,
∴,
解得:,
∴此时点M的坐标为或,
当点M的坐标为时,根据中点坐标公式可知:
,解得:,
∴此时点P的坐标为;
当点M的坐标为时,
根据中点坐标公式可知:
,解得:,
∴此时点P的坐标为;
②当为对角线时,,
则,
∴,
解得:或,
∴此时点M的坐标为或,
当点M的坐标为时,根据中点坐标公式得:
,解得:,
∴此时点P的坐标为;
当点M的坐标为时,根据中点坐标公式得:
,解得:,
∴此时点P的坐标为;
③当为对角线时,,
则,
∴,
解得:,
∴此时点M的坐标为,根据中点坐标公式得:
,解得:,
∴此时点P的坐标为;
综上可知:满足条件的所有点P的坐标为或或或或.
25.【解】(1)解:∵满足,
∴,
∴;
(2)解:是正方形,,
,
,
,
过点作轴于点,则,
,,,
,
,,
在和中,,
,
,,
是菱形,
在中,,
,
,
菱形是正方形;
(3)解:,
,,
过点作轴于点,
轴,
,
,
,
又,
,
在中,,
,
,
在和中,,
,
,
在中,,
∵,
∴,
,
,
的坐标是.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若数据1,4,2,x,5的平均数是3,则中位数是( )
A.4 B.3 C.2 D.1
2.下列二次根式中是最简二次根式的是( )
A. B. C. D.
3.下列四组数中,不是勾股数的是( )
A.,, B.,,
C.,, D.,,
4.如图,在矩形中,对角线,相交于点,若要使矩形成为正方形,添加的条件不正确的是( )
A. B. C. D.
5.若一次函数的图象经过第一、三、四象限,则( )
A. B. C. D.
6.估计的值应在( )
A.2与3之间 B.3与4之间
C.4与5之间 D.5与6之间
7.的两边,满足,则是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.等腰直角三角形
8.如图,菱形中,,,则菱形的周长为( )
A. B. C. D.
9.如图1,四边形、均为正方形,且点,,在同一直线上,将正方形绕点逆时针旋转,如图2,点,,在同一直线点,连接,,.给出下列结论:①;②;③若,,则.其中正确的结论是( )
A.①② B.①③ C.②③ D.①②③
10.如图1,中,,点D是边上一点,过点D作交于点E,动点P从点D出发,以每秒1个单位长度的速度,按的路径匀速运动.设点P的运动时间为,的面积为S,S关于t的函数图象如图2所示,则的长为( )
A. B. C.2 D.
二、填空题(每小题3分,满分18分)
11.平面直角坐标系中,点P的坐标为(1,4),则点P到原点的距离是 .
12.已知,则x2﹣4x﹣1的值为 .
13.一组数据的方差计算为:,则这组数据的平均数为 .
14.平面直角坐标系中,点M(﹣3,4)到原点的距离是 .
15.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为 .
16.如图,在△ABC中,D为AC上一点,连接BD,∠A+∠C=∠ABD,BD=BA=2,BC=5,则△ABC的面积是 .
人教版2024—2025学年八年级下学期数学期末复习调研与押题训练
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
姓名:____________ 学号:_____________座位号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:.
18.已知,如图,,,,,,
(1)求的长;
(2)求图形中阴影部分的面积.
19.已知关于的函数.
(1)若是的正比例函数,求的值;
(2)若,求该函数图象与轴的交点坐标.
20.某校八年级全体学生参加“奥运知识知多少”的测试(满分10分),从中随机抽取20名学生的成绩绘制成如下统计图.
(1)这20名学生成绩的中位数是_____,众数是_____,平均数是______;
(2)若成绩在9分及以上为优秀,该校八年级共有120名学生,估计成绩为优秀的学生有多少名?
21.已知:如图,矩形中,,将沿直线翻折,点落在点处,与相交于点,连接.
(1)求证:.
(2)连接,与的交点为,过作交于,连接.求证:四边形是矩形.
22.如图,四边形是菱形,对角线,相交于点O,于点H.
(1)若,求的度数;
(2)若,,求的长.
23.随着deepseek的AI技术开发,更大激活智能机器人应用市场,为了更方便的服务广大读者,某图书馆准备引进智能机器人服务读者,购进甲、乙两种型号的机器人,已知甲种型号的单价比乙种型号的机器人多3万元,经过调研发现130万购买的甲中型号机器人和100万购买的乙种型号的机器人数量一样.
(1)求甲乙两种型号的机器人的单价是多少万元?
(2)图书馆经过统筹安排,准备用不低于114万的资金购进甲、乙两种型号的机器人共10套(两种型号均有),则有几种购买方案,购买乙种智能机器人多少套,所花资金最少?
24.如图1,在平面直角坐标系中,坐标原点为O,直线交x轴于点A,点B的坐标为,点C的坐标为.
(1)求直线的解析式和点A的坐标;
(2)以点C为直角顶点作,射线交x轴的正半轴于点E,射线交y轴的负半轴于点F.当绕着点C旋转时,的值是否发生变化,若不变,求出它的值;若变化,求出它的变化范围;
(3)如图2,点M是x轴上的一个动点,点P是坐标平面内一点.若B、C、M、P四点能构成菱形,求出满足条件的所有点P的坐标。
25.如图,在平面直角坐标系中,满足,过点分别作轴于点,轴于点.
(1)______,______.
(2)如图1,点,分别在线段,上(不与端点重合),,连接,,以,为边向右侧作.若,,则是什么特殊四边形?请说明理由.
(3)如图2,过作,交轴正半轴于点,若,求点的坐标.
中小学教育资源及组卷应用平台
试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D D A B D D D D
二、填空题
11.【解答】解:由点P的坐标为(1,4),
则点P到原点的距离.
故答案为:.
12.【解答】解:∵,
∴x2﹣4x﹣1
=(x2﹣4x+4)﹣1﹣4
=(x﹣2)2﹣5
=(2﹣2)2﹣5
=()2﹣5
=5﹣5
=0.
故答案为:0.
13.【解答】解:由题意可知这组数据为5、3、6、4,
∴平均数为:(5+3+4+6)÷4=4.5.
故答案为:4.5.
14.【解答】解:作MA⊥x轴于A,则MA=4,OA=3.
则根据勾股定理,得OM=5.
故答案为5.
15.【解答】解:∵AECF为菱形,
∴∠FCO=∠ECO,
由折叠的性质可知,∠ECO=∠BCE,
又∠FCO+∠ECO+∠BCE=90°,
∴∠FCO=∠ECO=∠BCE=30°,
在Rt△EBC中,EC=2EB,
又EC=AE,
AB=AE+EB=3,
∴EB=1,EC=2,
∴Rt△BCE中,BCBE,
故答案为:.
16.【解答】解:延长CB,作AE⊥CB于点E,
∴∠EBA=∠BAC+∠C,
∵∠BAC+∠C=∠ABD,
∴∠EBA=∠ABD,
作AF⊥BD于点F,
∴AE=AF,
作BH⊥AD,
∵S△ABC BC AEAE,S△ABD BD AF=AF,
∴S△ABC:S△ABD=2:5,
∴AD:AC=2:5,
设AD=2x,
∴AC=5x,DC=3x,
∵BA=BD,
∴AH=DH=x,
∴HC=4x,
∴22﹣x2=52﹣(4x)2,
∴x,
∵BH2=22﹣()2,
∴BH,
∴S△ABC5.
故答案为:.
三、解答题
17.【解】解:原式
.
18.【解】(1)解:在中,;
(2)解:在中,,
.
∵,
.
19.【解】(1)解: 关于的函数是的正比例函数,
,解得.
(2)解:当时,该函数的表达式为,
令,得,解得:,
当时,函数图象与轴的交点坐标为.
20.【解】(1)解:由题意知,中位数是第10,11位数的平均数,即,
众数是9,
平均数为,
故答案为:8,9,;
(2)解:由题意知,(名),
答:估计该校120名学生中,成绩为优秀的学生有54名.
21.【解】(1)证明:矩形,
∴,.
∴,
∵沿直线翻折
.
.
,
∴.
∵,
∴,
∴.
.
.
在中,.
在中,.
又,
,
.
.
(2)证明:如图:
沿直线翻折,
.
,
,
,
,,
,
∴.
.
又.
.
,
,.
又,
.
,
∴四边形是平行四边形.
平行四边形是矩形.
22.【解】(1)解:∵四边形是菱形,
∴
∴;
(2)解:∵四边形是菱形
∴,,
∴在中,
∵,
∴,
∴.
23.【解】(1)解:设甲种型号的机器人的单价是x万元,则乙种型号的机器人的单价是万元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
∴(万元).
答:甲种型号的机器人的单价是13万元,乙种型号的机器人的单价是10万元;
(2)解:设购买乙种智能机器人m套,则购买甲种智能机器人套,
根据题意得:,
解得:,
又∵m,均为正整数,
∴m可以为1,2,3,4,5,
∴有5种购买方案.
设购买甲、乙两种型号的机器人共花费w万元,则,
即,
∵,
∴w随m的增大而减小,
∴当时,w取得最小值.
答:有5种购买方案,购买乙种智能机器人5套,所花资金最少.
24.【解】(1)解:设直线的解析式为:,
点,点在直线上,
,
解得,
直线的解析式为:;
把代入得:,
解得:,
∴;
(2)解:不变,理由如下:
过点C分别作x轴、y轴的垂线,垂足分别为M、N,如图,
则,
又,
,
,
,
,
,
,
,
在和中,
,
,
,
故的值不发生变化,值为6;
(3)解:设点M的坐标为,点P的坐标为,
∵,,
∴,
,
,
①为对角线时,
则,
∴,
解得:,
∴此时点M的坐标为或,
当点M的坐标为时,根据中点坐标公式可知:
,解得:,
∴此时点P的坐标为;
当点M的坐标为时,
根据中点坐标公式可知:
,解得:,
∴此时点P的坐标为;
②当为对角线时,,
则,
∴,
解得:或,
∴此时点M的坐标为或,
当点M的坐标为时,根据中点坐标公式得:
,解得:,
∴此时点P的坐标为;
当点M的坐标为时,根据中点坐标公式得:
,解得:,
∴此时点P的坐标为;
③当为对角线时,,
则,
∴,
解得:,
∴此时点M的坐标为,根据中点坐标公式得:
,解得:,
∴此时点P的坐标为;
综上可知:满足条件的所有点P的坐标为或或或或.
25.【解】(1)解:∵满足,
∴,
∴;
(2)解:是正方形,,
,
,
,
过点作轴于点,则,
,,,
,
,,
在和中,,
,
,,
是菱形,
在中,,
,
,
菱形是正方形;
(3)解:,
,,
过点作轴于点,
轴,
,
,
,
又,
,
在中,,
,
,
在和中,,
,
,
在中,,
∵,
∴,
,
,
的坐标是.
同课章节目录
