人教版2024—2025学年七年级下册数学期末考试全真模拟试卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年七年级下册数学期末考试全真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 815.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 12:59:20 | ||
图片预览




文档简介
人教版2024—2025学年七年级下册数学期末考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列调查中,适宜采用全面调查(普查)方式的是( )
A.对我国首架大型民用直升机各零部件的检查
B.对冷饮市场上冰淇淋质量情况的调查
C.对格力空调的市场占有率的调查
D.了解全国中学生的用眼卫生情况
2.不等式组的解集是( )
A. B. C. D.
3.如果是方程的一组解,那么代数式的值是( )
A.6 B.5 C. D.
4.《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”其大意是:用一根绳子去量一根木条,绳子还剩余尺;将绳子对折再量,木条还剩余1尺;问木条长多少尺?如果设木条长为x尺,绳子长为y尺,则下面所列方程组正确的是( )
A. B.
C. D.
5.将点沿x轴方向向左平移个单位,再沿y轴方向向上平移个单位,所得的点的坐标是( )
A. B. C. D.
6.下列各数中,无理数是( )
A. B. C. D.
7.有一个数值转换器,流程如图:当输入的x值为64时,输出的y值是( )
A. B. C. D.
8.能说明命题“两个锐角的和一定是钝角”是假命题的反例是( )
A. B.
C. D.
9.如图,已知,点B在上,点C在上,点A在上方,,点E在的反向延长线上,且,则与的数量关系是( )
A. B.
C. D.
10.若关于x的方程的解为非负整数,且关于x的不等式组无解,则所有满足条件的a的值之和是( )
A.7 B.6 C.4 D.0
二、填空题(6小题,每题3分,共18分)
11.年“五一”假期,青岛共接待游客人次.在这个数中“”的频数是 .
12.若关于x的不等式组有且仅有3个整数解,则a的取值范围为 .
13.满足,且,则 .
14.若点在轴上,则点的坐标是 .
15.已知一个正数的两个平方根分别是和,那么这个正数是 .
中小学教育资源及组卷应用平台
16.如图,在中,,,,,将沿直线向右平移个单位得到,与相交于点G,,连接,,则 .试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
第II卷
人教版2024—2025学年七年级下册数学期末考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组:,并求其整数解.
18.解方程组:
(1) (2)
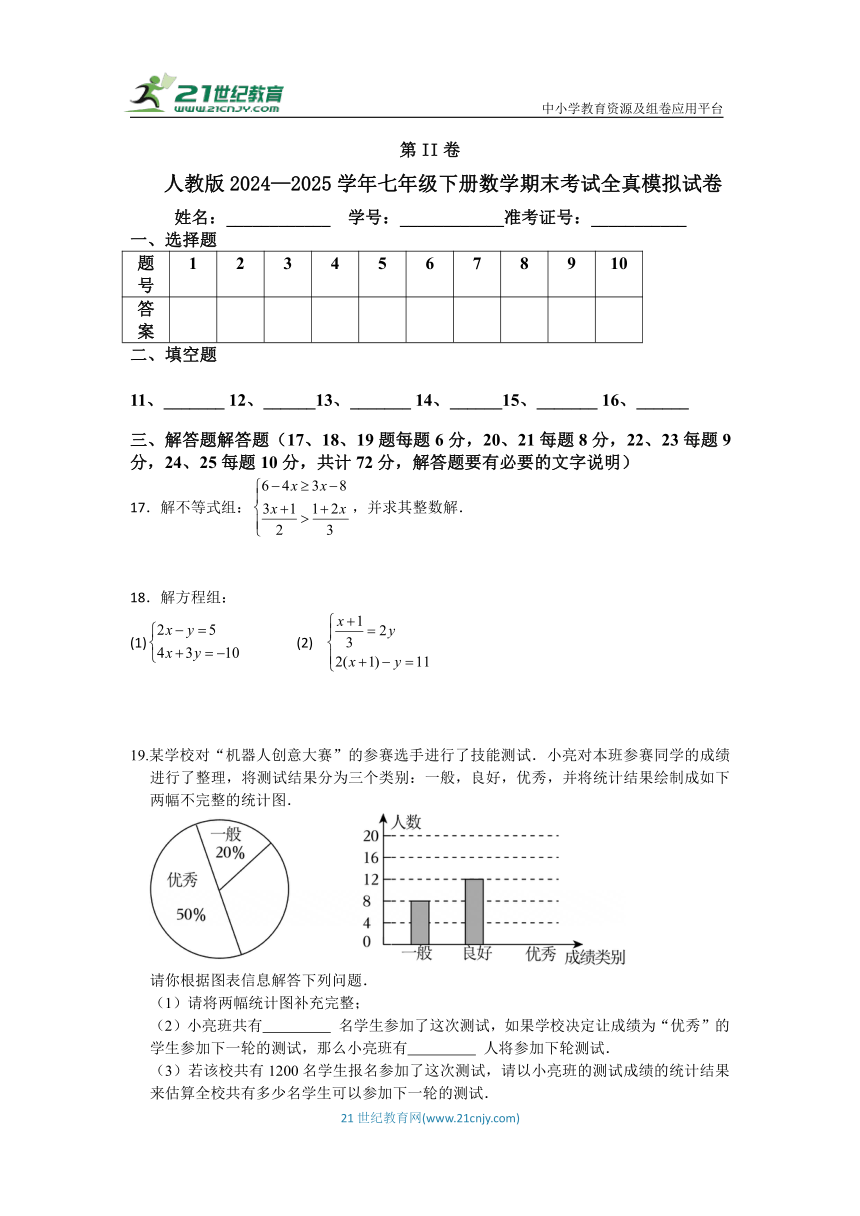
19.某学校对“机器人创意大赛”的参赛选手进行了技能测试.小亮对本班参赛同学的成绩进行了整理,将测试结果分为三个类别:一般,良好,优秀,并将统计结果绘制成如下两幅不完整的统计图.
请你根据图表信息解答下列问题.
(1)请将两幅统计图补充完整;
(2)小亮班共有 名学生参加了这次测试,如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有 人将参加下轮测试.
(3)若该校共有1200名学生报名参加了这次测试,请以小亮班的测试成绩的统计结果来估算全校共有多少名学生可以参加下一轮的测试.
20.若x,y是实数,且.
(1)求x,y的值;
(2)求的值.
21.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).
(1)点A的坐标是 点B的坐标是 .
(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;
(3)求三角形ABC的面积.
22.苹果的进价是元/千克,香梨的进价是2元/千克;李老板购进苹果的重量比香梨重量的3倍多20千克,一共花费420元;为方便销售,定价均为7元/千克.(销售量取整数)
(1)李老板购进苹果和香梨各多少千克?
(2)前4天,平均每天卖出苹果和香梨共50千克,若每天利润大于268元,且苹果的平均日销售量小于香梨平均日销售量的3倍.问:这4天苹果和香梨的平均日销售量分别是多少千克?
23.如图,已知,,点在直线上且.
(1)求证:;
(2)若,求的度数.
24.我们把关于x、y的两个二元一次方程与叫作互为共轭二元一次方程:二元一次方程组,叫做关于x、y共轭二元一次方程组.例如:与互为共轭二元一次方程,二元一次方程组,叫做关于x、y共轭二元一次方程组;与互为共轭二元一次方程,二元一次方程组,叫做关于、的共轭二元一次方程组.
(1)若关于x、y的方程组,为共轭方程组,则 , ;
(2)若二元一次方程中x、y的值满足下列表格:
则这个方程的共轭二元一次方程是 .
(3)解下列方程组(直接写出方程组的解即可):的解为 .
(4)发现:若方程组是共轭方程组,且方程组的解是,请化简.
25.已知关于的不等式组.
(1)当时,求该不等式组的解集.
(2)若该不等式组有且只有个整数解,求的所有整数解的和.
(3)在()的条件下,已知关于的方程组的解满足不等式,求的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C A C B B D C C
二、填空题
11.【解】解:∵在这个数中“”出现次,
∴在这个数中“”的频数是,
故答案为:.
12.【解】解:解不等式得
∵关于x的不等式组有且仅有3个整数解,
∴不等式组的3个整数解是:0,1,2,
∴,
故答案为:.
13.【解】解:
得:,解得,
把滴入①得:,解得,
∴原方程组的解为,
∵,
∴,
解得,
故答案为:.
14.【解】解:∵点在轴上,
∴
解得;
∴
∴点的坐标是,
故答案为:.
15.【解】解:∵一个正数的两个平方根分别为和,
∴
解得:,
∴,
∴这个正数为.
故答案为:.
16.【解】解:如图所示,延长交于H,连接,
由平移的性质可得,,
∴;
∵在中,,,,,
∴,
∴;
∵,
∴,
同理可得,
∴,
∴,
∵,
∴点A到的距离等于点E到的距离,,
又∵,
∴,
∴,
故答案为;72.
三、解答题
17.解:,
解不等式,得.
解不等式,得.
原不等式组的解集是.
该不等式组的整数解为,,.
18.(1)解:,
得,
,
,
将代入①中,得,
,
;
(2)解:即,
将代入得,
,
,
将代入①中,得,
.
19.【解答】解:(1)∵参加测试的总人数:8÷20%=40人,
∴优秀人数为40×50%=20人,良好所占百分比为30%;
补全图形如下:
(2)小亮班共有40名学生参加了这次测试,
如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有20人将参加下轮测试.
故答案为:40,20;
(3)若该校共有1200名学生,可以参加下一轮测试的人数为1200×50%=600人.
20.【解答】解:(1)∵.
∴4x﹣16≥0,16﹣4x≥0,
∴4x﹣16=0,
∴x=4,
则y=3,
(2)∵x=4,y=3,
∴.
21.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1);(4,3);
(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)三角形ABC的面积=3×43×13×12×4=5.
22.【解】(1)解:设李老板购进香梨千克,苹果千克,
根据题意得:,
解得,
则(千克),
答:李老板购进香梨千克,苹果千克;
(2)解:设这4天平均每天卖出苹果千克,则平均每天卖出香梨千克,
每天利润大于268元,
,
解得,
苹果的平均日销售量小于香梨平均日销售量的3倍.
,
解得,
综上,,且销售量取整数,
,则(千克),
答:这4天平均每天卖出苹果千克,则平均每天卖出香梨千克.
23.【解】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,,
∴,
∵,
∴,
∵,
∴,
∴.
24.(1)解:由定义可得: , ,
∴, ,
故答案为:,;
(2)解:将, 代入, 得,解得,
∴二元一次方程为,
∴共轭二元一次方程为:,
故答案为:;
(3)解:
①②得: , 即③,
①③得: ,
解得,
将代入③得,
∴方程组的解为: ,
故答案为: ;
(4)解:∵由定义可得
∴
∵方程组是共轭方程组,
∴,
①②得,
,
又∵方程组的解是,
,即,
.
25.(1)解:当时,不等式组为,
由得,,
由得,,
∴不等式组的解集为;
(2)解:,
由得,,
由得,,
∴不等式组的解集为,
∵不等式组有且只有个整数解,
∴,
即,
解得,
∴的整数解为,,,
∴;
(3)解:,
方程组化简得,,
得,,
解得,
把代入得,,
∴,
∴方程组的解为,
把,代入不等式得,,
解得.
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列调查中,适宜采用全面调查(普查)方式的是( )
A.对我国首架大型民用直升机各零部件的检查
B.对冷饮市场上冰淇淋质量情况的调查
C.对格力空调的市场占有率的调查
D.了解全国中学生的用眼卫生情况
2.不等式组的解集是( )
A. B. C. D.
3.如果是方程的一组解,那么代数式的值是( )
A.6 B.5 C. D.
4.《孙子算经》中记载:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”其大意是:用一根绳子去量一根木条,绳子还剩余尺;将绳子对折再量,木条还剩余1尺;问木条长多少尺?如果设木条长为x尺,绳子长为y尺,则下面所列方程组正确的是( )
A. B.
C. D.
5.将点沿x轴方向向左平移个单位,再沿y轴方向向上平移个单位,所得的点的坐标是( )
A. B. C. D.
6.下列各数中,无理数是( )
A. B. C. D.
7.有一个数值转换器,流程如图:当输入的x值为64时,输出的y值是( )
A. B. C. D.
8.能说明命题“两个锐角的和一定是钝角”是假命题的反例是( )
A. B.
C. D.
9.如图,已知,点B在上,点C在上,点A在上方,,点E在的反向延长线上,且,则与的数量关系是( )
A. B.
C. D.
10.若关于x的方程的解为非负整数,且关于x的不等式组无解,则所有满足条件的a的值之和是( )
A.7 B.6 C.4 D.0
二、填空题(6小题,每题3分,共18分)
11.年“五一”假期,青岛共接待游客人次.在这个数中“”的频数是 .
12.若关于x的不等式组有且仅有3个整数解,则a的取值范围为 .
13.满足,且,则 .
14.若点在轴上,则点的坐标是 .
15.已知一个正数的两个平方根分别是和,那么这个正数是 .
中小学教育资源及组卷应用平台
16.如图,在中,,,,,将沿直线向右平移个单位得到,与相交于点G,,连接,,则 .试卷第1页,共3页
21世纪教育网(www.21cnjy.com)
第II卷
人教版2024—2025学年七年级下册数学期末考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解不等式组:,并求其整数解.
18.解方程组:
(1) (2)
19.某学校对“机器人创意大赛”的参赛选手进行了技能测试.小亮对本班参赛同学的成绩进行了整理,将测试结果分为三个类别:一般,良好,优秀,并将统计结果绘制成如下两幅不完整的统计图.
请你根据图表信息解答下列问题.
(1)请将两幅统计图补充完整;
(2)小亮班共有 名学生参加了这次测试,如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有 人将参加下轮测试.
(3)若该校共有1200名学生报名参加了这次测试,请以小亮班的测试成绩的统计结果来估算全校共有多少名学生可以参加下一轮的测试.
20.若x,y是实数,且.
(1)求x,y的值;
(2)求的值.
21.如图,在平面直角坐标系中,三角形ABC的顶点都在网格点上,其中点C的坐标为(1,2).
(1)点A的坐标是 点B的坐标是 .
(2)画出将三角形ABC先向左平移2个单位长度,再向上平移1个单位长度所得到的三角形A'B'C'.请写出三角形A'B'C'的三个顶点坐标;
(3)求三角形ABC的面积.
22.苹果的进价是元/千克,香梨的进价是2元/千克;李老板购进苹果的重量比香梨重量的3倍多20千克,一共花费420元;为方便销售,定价均为7元/千克.(销售量取整数)
(1)李老板购进苹果和香梨各多少千克?
(2)前4天,平均每天卖出苹果和香梨共50千克,若每天利润大于268元,且苹果的平均日销售量小于香梨平均日销售量的3倍.问:这4天苹果和香梨的平均日销售量分别是多少千克?
23.如图,已知,,点在直线上且.
(1)求证:;
(2)若,求的度数.
24.我们把关于x、y的两个二元一次方程与叫作互为共轭二元一次方程:二元一次方程组,叫做关于x、y共轭二元一次方程组.例如:与互为共轭二元一次方程,二元一次方程组,叫做关于x、y共轭二元一次方程组;与互为共轭二元一次方程,二元一次方程组,叫做关于、的共轭二元一次方程组.
(1)若关于x、y的方程组,为共轭方程组,则 , ;
(2)若二元一次方程中x、y的值满足下列表格:
则这个方程的共轭二元一次方程是 .
(3)解下列方程组(直接写出方程组的解即可):的解为 .
(4)发现:若方程组是共轭方程组,且方程组的解是,请化简.
25.已知关于的不等式组.
(1)当时,求该不等式组的解集.
(2)若该不等式组有且只有个整数解,求的所有整数解的和.
(3)在()的条件下,已知关于的方程组的解满足不等式,求的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C A C B B D C C
二、填空题
11.【解】解:∵在这个数中“”出现次,
∴在这个数中“”的频数是,
故答案为:.
12.【解】解:解不等式得
∵关于x的不等式组有且仅有3个整数解,
∴不等式组的3个整数解是:0,1,2,
∴,
故答案为:.
13.【解】解:
得:,解得,
把滴入①得:,解得,
∴原方程组的解为,
∵,
∴,
解得,
故答案为:.
14.【解】解:∵点在轴上,
∴
解得;
∴
∴点的坐标是,
故答案为:.
15.【解】解:∵一个正数的两个平方根分别为和,
∴
解得:,
∴,
∴这个正数为.
故答案为:.
16.【解】解:如图所示,延长交于H,连接,
由平移的性质可得,,
∴;
∵在中,,,,,
∴,
∴;
∵,
∴,
同理可得,
∴,
∴,
∵,
∴点A到的距离等于点E到的距离,,
又∵,
∴,
∴,
故答案为;72.
三、解答题
17.解:,
解不等式,得.
解不等式,得.
原不等式组的解集是.
该不等式组的整数解为,,.
18.(1)解:,
得,
,
,
将代入①中,得,
,
;
(2)解:即,
将代入得,
,
,
将代入①中,得,
.
19.【解答】解:(1)∵参加测试的总人数:8÷20%=40人,
∴优秀人数为40×50%=20人,良好所占百分比为30%;
补全图形如下:
(2)小亮班共有40名学生参加了这次测试,
如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有20人将参加下轮测试.
故答案为:40,20;
(3)若该校共有1200名学生,可以参加下一轮测试的人数为1200×50%=600人.
20.【解答】解:(1)∵.
∴4x﹣16≥0,16﹣4x≥0,
∴4x﹣16=0,
∴x=4,
则y=3,
(2)∵x=4,y=3,
∴.
21.【解答】解:(1)A(2,﹣1),B(4,3);
故答案为(2,﹣1);(4,3);
(2)如图,三角形A'B'C'为所作;A′(0,0),B′(2,4),C′(﹣1,3);
(3)三角形ABC的面积=3×43×13×12×4=5.
22.【解】(1)解:设李老板购进香梨千克,苹果千克,
根据题意得:,
解得,
则(千克),
答:李老板购进香梨千克,苹果千克;
(2)解:设这4天平均每天卖出苹果千克,则平均每天卖出香梨千克,
每天利润大于268元,
,
解得,
苹果的平均日销售量小于香梨平均日销售量的3倍.
,
解得,
综上,,且销售量取整数,
,则(千克),
答:这4天平均每天卖出苹果千克,则平均每天卖出香梨千克.
23.【解】(1)证明:∵,
∴,
∵,
∴,
∴;
(2)解:∵,,
∴,
∵,
∴,
∵,
∴,
∴.
24.(1)解:由定义可得: , ,
∴, ,
故答案为:,;
(2)解:将, 代入, 得,解得,
∴二元一次方程为,
∴共轭二元一次方程为:,
故答案为:;
(3)解:
①②得: , 即③,
①③得: ,
解得,
将代入③得,
∴方程组的解为: ,
故答案为: ;
(4)解:∵由定义可得
∴
∵方程组是共轭方程组,
∴,
①②得,
,
又∵方程组的解是,
,即,
.
25.(1)解:当时,不等式组为,
由得,,
由得,,
∴不等式组的解集为;
(2)解:,
由得,,
由得,,
∴不等式组的解集为,
∵不等式组有且只有个整数解,
∴,
即,
解得,
∴的整数解为,,,
∴;
(3)解:,
方程组化简得,,
得,,
解得,
把代入得,,
∴,
∴方程组的解为,
把,代入不等式得,,
解得.
同课章节目录
