人教版2024—2025学年七年级下册数学期末复习卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年七年级下册数学期末复习卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 789.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 13:01:47 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年七年级下册数学期末复习卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.某校八年级()班名学生的健康状况被分成组,第1组的频数是,第,组的频率之和为,第组的频率是,则第组的频数是( )
A. B. C. D.
2.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
3.在下列方程组:①,②,③,④,⑤中,是二元一次方程组的是( )
A.①②⑤ B.①②④ C.①②③ D.①②③⑤
4.在平面直角坐标系中,点在第二象限内,则a的取值可以是( )
A.1 B. C.3 D.4或
5.已知,则x的值为( )
A.4 B.2或 C.或4 D.
6.如图,以下四个条件:①;②;③;④平分,其中能判断直线的有( )
A.4个 B.3个 C.2个 D.1个
7.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行 B.相等的角是对顶角
C.两条直线被第三条直线所截,同位角相等 D.若,,则
8.《九章算术》中记载了这样一道题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,问牛和羊各值多少金?设每头牛值x金,每只羊值y金,可列方程组为( )
A. B. C. D.
9.如图,将三角形向右平移得到三角形,如果四边形的周长是,那么三角形的周长是( )
B.
C. D.
10.已知a,b,c是三个非负数,且满足,设的最大值为m,最小值为n,则的值是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.调查名学生的身高,列频数分布表时,学生的身高分布在个小组中,第一,二,三,五组的数据个数分别是,,,,则第四组的频率是 .
12.已知,则 .
13.已知点,且点到两坐标轴的距离相等,则点的坐标为
14.若,为实数,且满足,则 .
15.如图,直线a,b被直线c所截,若,,则 .
16.若方程组的解为,则方程组的解为.利用上面的解题经验,解决下面问题:若不等式组的解集为,则不等式组的解集为 .
第II卷
人教版2024—2025学年七年级下册数学期末复习卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解方程组;
(2)解不等式组,并写出它的整数解.
18.(1)计算:;
(2)求等式中x的值:(x﹣1)2=16.
19.若x,y是实数,且.
(1)求x,y的值;
(2)求的值.
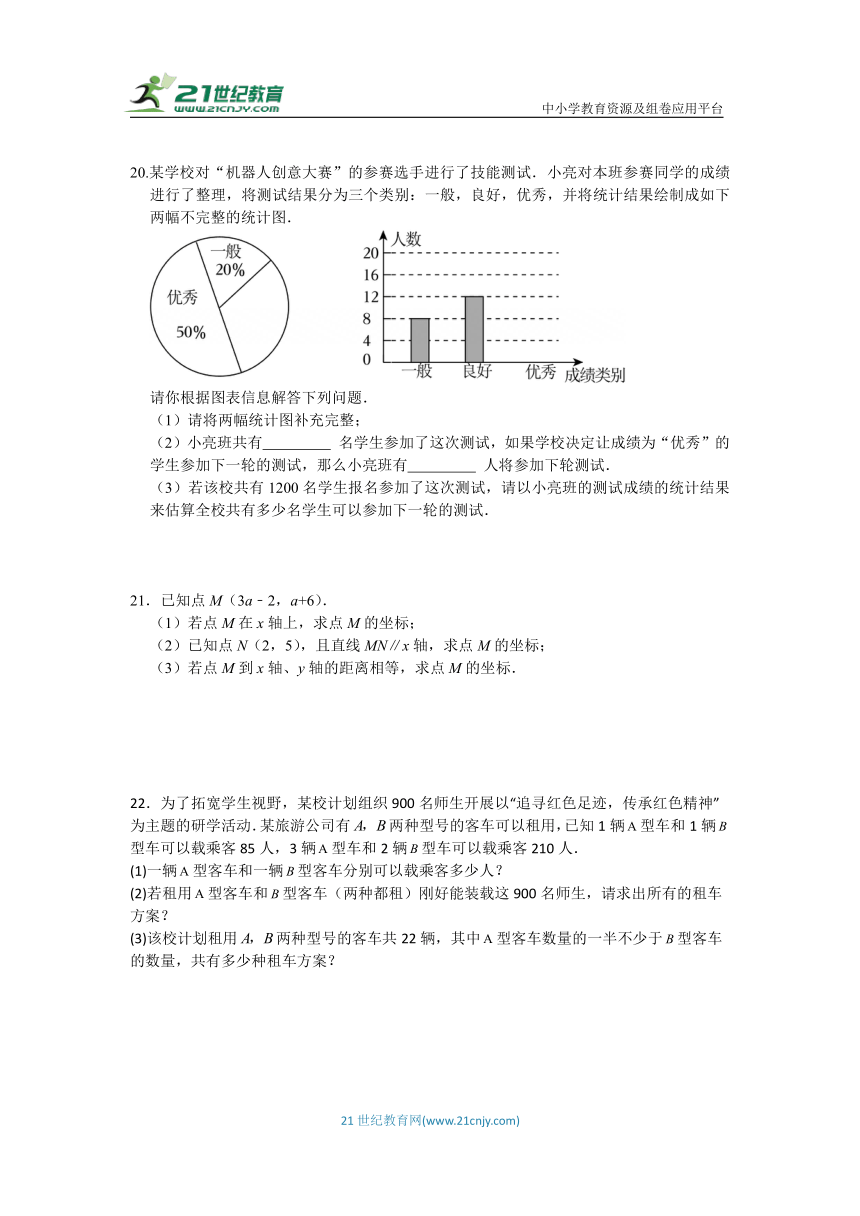
20.某学校对“机器人创意大赛”的参赛选手进行了技能测试.小亮对本班参赛同学的成绩进行了整理,将测试结果分为三个类别:一般,良好,优秀,并将统计结果绘制成如下两幅不完整的统计图.
请你根据图表信息解答下列问题.
(1)请将两幅统计图补充完整;
(2)小亮班共有 名学生参加了这次测试,如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有 人将参加下轮测试.
(3)若该校共有1200名学生报名参加了这次测试,请以小亮班的测试成绩的统计结果来估算全校共有多少名学生可以参加下一轮的测试.
21.已知点M(3a﹣2,a+6).
(1)若点M在x轴上,求点M的坐标;
(2)已知点N(2,5),且直线MN∥x轴,求点M的坐标;
(3)若点M到x轴、y轴的距离相等,求点M的坐标.
22.为了拓宽学生视野,某校计划组织900名师生开展以“追寻红色足迹,传承红色精神”为主题的研学活动.某旅游公司有两种型号的客车可以租用,已知1辆型车和1辆型车可以载乘客85人,3辆型车和2辆型车可以载乘客210人.
(1)一辆型客车和一辆型客车分别可以载乘客多少人?
(2)若租用型客车和型客车(两种都租)刚好能装载这900名师生,请求出所有的租车方案?
(3)该校计划租用两种型号的客车共22辆,其中型客车数量的一半不少于型客车的数量,共有多少种租车方案?
23.已知关于的不等式组.
(1)当时,求该不等式组的解集.
(2)若该不等式组有且只有个整数解,求的所有整数解的和.
(3)在()的条件下,已知关于的方程组的解满足不等式,求的取值范围.
24.已知:在平面直角坐标系中点,点 ,且满足.
(1)求点,点的坐标;
(2)已知点,点从点出发沿轴负方向以1个单位长度/s的速度移动,同 时,点从点出发,沿轴负方向以1.5个单位长度/s的速度移动.如图1, 求点移动的 时间;
(3)在(3)的条件和结论下,如图2所示,设交轴于点,作,的角平分线交于点,求此时的值.
25.新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“相依方程”,例如:方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“相依方程”.
(1)在方程①:②;③中,不等式组的“相依方程”是______;(填序号)
(2)若关于x的方程是不等式组的“相依方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“相依方程”,且此时不等式组有5个整数解,试求m的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A B C C D D B D
二、填空题
11.【解】解:共有名学生,第一,二,三,五组的人数分别是,,,,
第四组的人数是,
第四组的频率是.
故答案为:.
12.【解】解:∵,
∴,
解得:,
∴.
故答案为:1.
13.【解】解:∵点到两坐标轴的距离相等,且点,
∴,
∴或,
解得:或,
∴点A的坐标为:或;
故答案为:或.
14.【解】解:∵,
∴,,
∴,
∴,
故答案为:.
15.【解】解:如图,
∵,
∴,
∴,,
∴,
∵,
∴,
故答案为:.
16.【解】解:不等式组,整理得
,
∴,
∴,
∵不等式组的解集为,
∴,
∴,
解得,
故答案为:.
三、解答题
17.【解答】解:(1),
①﹣②×6,得﹣10x=﹣15,
解得x=﹣,
把x=﹣代入②.
故原方程组的解为;
(2),
解不等式①,得:x≥6,
解不等式②,得:x<3,
则不等式组的解集为:1≤x<8,它的整数解为1,2.
18.【解答】解:(1)
=2+﹣2﹣2
=﹣;
(2)开平方,得x﹣1=±4,
解得x=4或x=﹣3.
19.【解答】解:(1)∵.
∴4x﹣16≥0,16﹣4x≥0,
∴4x﹣16=0,
∴x=4,
则y=3,
(2)∵x=4,y=3,
∴.
20.【解答】解:(1)∵参加测试的总人数:8÷20%=40人,
∴优秀人数为40×50%=20人,良好所占百分比为30%;
补全图形如下:
(2)小亮班共有40名学生参加了这次测试,
如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有20人将参加下轮测试.
故答案为:40,20;
(3)若该校共有1200名学生,可以参加下一轮测试的人数为1200×50%=600人.
21.【解答】解:(1)∵点M在x轴上,
∴a+6=0,
∴a=﹣6,3a﹣2=﹣18﹣2=﹣20,
∴点M的坐标是(﹣20,0);
(2)∵直线MN∥x轴,a+6=5,
解得a=﹣1,3a﹣2=3×(﹣1)﹣2=﹣5,
所以,点M的坐标为(﹣5,5).
(3)∵点M到x轴、y轴的距离相等.
∴3a﹣2=a+6或3a﹣2+a+6=0,
解得a=4或a=﹣1.
∴3a﹣2=a+6=10或3a﹣2=﹣5,a+6=5.
∴点M的坐标为(10,10)或(﹣5,5).
22.(1)解:设一辆A型客车可以载乘客x人,一辆B型客车可以载乘客y人.
根据题意,得,
解得,
答:一辆A型客车可以载乘客40人,一辆B型客车可以载乘客45人;
(2)解:设租用a辆A型客车,租用b辆B型客车,
根据题意,得,则,
∵a、b是正整数,
∴或,
故有两种租车方案:方案一:租用9辆A型客车,租用12辆B型客车;方案二:租用18辆A型客车,租用4辆B型客车
(3)解:设租用m辆A型客车,则租用辆B型客车,
根据题意,得,
解得,
∵为正整数,
∴m的值可以为15,16,17,18,
∴共有4种租车方案:
方案一:租用15辆A型客车,7辆B型客车,
方案二:租用16辆A型客车,6辆B型客车,
方案三:租用17辆A型客车,5辆B型客车,
方案二:租用18辆A型客车,4辆B型客车.
23.(1)解:当时,不等式组为,
由得,,
由得,,
∴不等式组的解集为;
(2)解:,
由得,,
由得,,
∴不等式组的解集为,
∵不等式组有且只有个整数解,
∴,
即,
解得,
∴的整数解为,,,
∴;
(3)解:,
方程组化简得,,
得,,
解得,
把代入得,,
∴,
∴方程组的解为,
把,代入不等式得,,
解得.
24(1)解:∵,
∴,
解得,
∴
(2)解:由(1)可知,
即,
则,,
如图,过点Q作于H.
设点P的运动时间为t秒.则,,,,
,
∵,
∴,
∴;
(3)解:由(2)可知,,
∴,
∵平分,平分,
∴, ,
∴,
过点N作,则
∵轴,轴,
∴,
∴,
∴.
25.(1)解:①,
整理得:,
解得:;
②,
解得:;
③,
解得:;
,
解不等式可得:,
解不等式可得:,
所以不等式组的解集为:;
根据新定义可得:方程①是不等式组的“相依方程”.
故答案为:①;
(2)解:,
由①得:,
由②得:,
所以不等式组的解集为:,
,
,
根据“相依方程”的含义可得:
,
,
解得:;
(3)解:,
由①得:,
由②得:,
∴不等式组的解集为:,
此时不等式组有5个整数解,
令整数的值为:,,,,,
,
∴,
则,
解得:,而为整数,则或0,
当时,,
∴,
因为,
解得:,
根据“相依方程”的含义可得:,
解可得:,
解可得:,
所以不等式组的解集为:;
当时,,
∴,
综上:.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年七年级下册数学期末复习卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.某校八年级()班名学生的健康状况被分成组,第1组的频数是,第,组的频率之和为,第组的频率是,则第组的频数是( )
A. B. C. D.
2.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
3.在下列方程组:①,②,③,④,⑤中,是二元一次方程组的是( )
A.①②⑤ B.①②④ C.①②③ D.①②③⑤
4.在平面直角坐标系中,点在第二象限内,则a的取值可以是( )
A.1 B. C.3 D.4或
5.已知,则x的值为( )
A.4 B.2或 C.或4 D.
6.如图,以下四个条件:①;②;③;④平分,其中能判断直线的有( )
A.4个 B.3个 C.2个 D.1个
7.下列说法正确的是( )
A.过一点有且只有一条直线与已知直线平行 B.相等的角是对顶角
C.两条直线被第三条直线所截,同位角相等 D.若,,则
8.《九章算术》中记载了这样一道题:牛5头和羊2只共值10金,牛2头和羊5只共值8金,问牛和羊各值多少金?设每头牛值x金,每只羊值y金,可列方程组为( )
A. B. C. D.
9.如图,将三角形向右平移得到三角形,如果四边形的周长是,那么三角形的周长是( )
B.
C. D.
10.已知a,b,c是三个非负数,且满足,设的最大值为m,最小值为n,则的值是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.调查名学生的身高,列频数分布表时,学生的身高分布在个小组中,第一,二,三,五组的数据个数分别是,,,,则第四组的频率是 .
12.已知,则 .
13.已知点,且点到两坐标轴的距离相等,则点的坐标为
14.若,为实数,且满足,则 .
15.如图,直线a,b被直线c所截,若,,则 .
16.若方程组的解为,则方程组的解为.利用上面的解题经验,解决下面问题:若不等式组的解集为,则不等式组的解集为 .
第II卷
人教版2024—2025学年七年级下册数学期末复习卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.(1)解方程组;
(2)解不等式组,并写出它的整数解.
18.(1)计算:;
(2)求等式中x的值:(x﹣1)2=16.
19.若x,y是实数,且.
(1)求x,y的值;
(2)求的值.
20.某学校对“机器人创意大赛”的参赛选手进行了技能测试.小亮对本班参赛同学的成绩进行了整理,将测试结果分为三个类别:一般,良好,优秀,并将统计结果绘制成如下两幅不完整的统计图.
请你根据图表信息解答下列问题.
(1)请将两幅统计图补充完整;
(2)小亮班共有 名学生参加了这次测试,如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有 人将参加下轮测试.
(3)若该校共有1200名学生报名参加了这次测试,请以小亮班的测试成绩的统计结果来估算全校共有多少名学生可以参加下一轮的测试.
21.已知点M(3a﹣2,a+6).
(1)若点M在x轴上,求点M的坐标;
(2)已知点N(2,5),且直线MN∥x轴,求点M的坐标;
(3)若点M到x轴、y轴的距离相等,求点M的坐标.
22.为了拓宽学生视野,某校计划组织900名师生开展以“追寻红色足迹,传承红色精神”为主题的研学活动.某旅游公司有两种型号的客车可以租用,已知1辆型车和1辆型车可以载乘客85人,3辆型车和2辆型车可以载乘客210人.
(1)一辆型客车和一辆型客车分别可以载乘客多少人?
(2)若租用型客车和型客车(两种都租)刚好能装载这900名师生,请求出所有的租车方案?
(3)该校计划租用两种型号的客车共22辆,其中型客车数量的一半不少于型客车的数量,共有多少种租车方案?
23.已知关于的不等式组.
(1)当时,求该不等式组的解集.
(2)若该不等式组有且只有个整数解,求的所有整数解的和.
(3)在()的条件下,已知关于的方程组的解满足不等式,求的取值范围.
24.已知:在平面直角坐标系中点,点 ,且满足.
(1)求点,点的坐标;
(2)已知点,点从点出发沿轴负方向以1个单位长度/s的速度移动,同 时,点从点出发,沿轴负方向以1.5个单位长度/s的速度移动.如图1, 求点移动的 时间;
(3)在(3)的条件和结论下,如图2所示,设交轴于点,作,的角平分线交于点,求此时的值.
25.新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“相依方程”,例如:方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“相依方程”.
(1)在方程①:②;③中,不等式组的“相依方程”是______;(填序号)
(2)若关于x的方程是不等式组的“相依方程”,求k的取值范围;
(3)若关于x的方程是关于x的不等式组的“相依方程”,且此时不等式组有5个整数解,试求m的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A B C C D D B D
二、填空题
11.【解】解:共有名学生,第一,二,三,五组的人数分别是,,,,
第四组的人数是,
第四组的频率是.
故答案为:.
12.【解】解:∵,
∴,
解得:,
∴.
故答案为:1.
13.【解】解:∵点到两坐标轴的距离相等,且点,
∴,
∴或,
解得:或,
∴点A的坐标为:或;
故答案为:或.
14.【解】解:∵,
∴,,
∴,
∴,
故答案为:.
15.【解】解:如图,
∵,
∴,
∴,,
∴,
∵,
∴,
故答案为:.
16.【解】解:不等式组,整理得
,
∴,
∴,
∵不等式组的解集为,
∴,
∴,
解得,
故答案为:.
三、解答题
17.【解答】解:(1),
①﹣②×6,得﹣10x=﹣15,
解得x=﹣,
把x=﹣代入②.
故原方程组的解为;
(2),
解不等式①,得:x≥6,
解不等式②,得:x<3,
则不等式组的解集为:1≤x<8,它的整数解为1,2.
18.【解答】解:(1)
=2+﹣2﹣2
=﹣;
(2)开平方,得x﹣1=±4,
解得x=4或x=﹣3.
19.【解答】解:(1)∵.
∴4x﹣16≥0,16﹣4x≥0,
∴4x﹣16=0,
∴x=4,
则y=3,
(2)∵x=4,y=3,
∴.
20.【解答】解:(1)∵参加测试的总人数:8÷20%=40人,
∴优秀人数为40×50%=20人,良好所占百分比为30%;
补全图形如下:
(2)小亮班共有40名学生参加了这次测试,
如果学校决定让成绩为“优秀”的学生参加下一轮的测试,那么小亮班有20人将参加下轮测试.
故答案为:40,20;
(3)若该校共有1200名学生,可以参加下一轮测试的人数为1200×50%=600人.
21.【解答】解:(1)∵点M在x轴上,
∴a+6=0,
∴a=﹣6,3a﹣2=﹣18﹣2=﹣20,
∴点M的坐标是(﹣20,0);
(2)∵直线MN∥x轴,a+6=5,
解得a=﹣1,3a﹣2=3×(﹣1)﹣2=﹣5,
所以,点M的坐标为(﹣5,5).
(3)∵点M到x轴、y轴的距离相等.
∴3a﹣2=a+6或3a﹣2+a+6=0,
解得a=4或a=﹣1.
∴3a﹣2=a+6=10或3a﹣2=﹣5,a+6=5.
∴点M的坐标为(10,10)或(﹣5,5).
22.(1)解:设一辆A型客车可以载乘客x人,一辆B型客车可以载乘客y人.
根据题意,得,
解得,
答:一辆A型客车可以载乘客40人,一辆B型客车可以载乘客45人;
(2)解:设租用a辆A型客车,租用b辆B型客车,
根据题意,得,则,
∵a、b是正整数,
∴或,
故有两种租车方案:方案一:租用9辆A型客车,租用12辆B型客车;方案二:租用18辆A型客车,租用4辆B型客车
(3)解:设租用m辆A型客车,则租用辆B型客车,
根据题意,得,
解得,
∵为正整数,
∴m的值可以为15,16,17,18,
∴共有4种租车方案:
方案一:租用15辆A型客车,7辆B型客车,
方案二:租用16辆A型客车,6辆B型客车,
方案三:租用17辆A型客车,5辆B型客车,
方案二:租用18辆A型客车,4辆B型客车.
23.(1)解:当时,不等式组为,
由得,,
由得,,
∴不等式组的解集为;
(2)解:,
由得,,
由得,,
∴不等式组的解集为,
∵不等式组有且只有个整数解,
∴,
即,
解得,
∴的整数解为,,,
∴;
(3)解:,
方程组化简得,,
得,,
解得,
把代入得,,
∴,
∴方程组的解为,
把,代入不等式得,,
解得.
24(1)解:∵,
∴,
解得,
∴
(2)解:由(1)可知,
即,
则,,
如图,过点Q作于H.
设点P的运动时间为t秒.则,,,,
,
∵,
∴,
∴;
(3)解:由(2)可知,,
∴,
∵平分,平分,
∴, ,
∴,
过点N作,则
∵轴,轴,
∴,
∴,
∴.
25.(1)解:①,
整理得:,
解得:;
②,
解得:;
③,
解得:;
,
解不等式可得:,
解不等式可得:,
所以不等式组的解集为:;
根据新定义可得:方程①是不等式组的“相依方程”.
故答案为:①;
(2)解:,
由①得:,
由②得:,
所以不等式组的解集为:,
,
,
根据“相依方程”的含义可得:
,
,
解得:;
(3)解:,
由①得:,
由②得:,
∴不等式组的解集为:,
此时不等式组有5个整数解,
令整数的值为:,,,,,
,
∴,
则,
解得:,而为整数,则或0,
当时,,
∴,
因为,
解得:,
根据“相依方程”的含义可得:,
解可得:,
解可得:,
所以不等式组的解集为:;
当时,,
∴,
综上:.
21世纪教育网(www.21cnjy.com)
同课章节目录
