人教版2024—2025学年七年级下册数学期末素养检测卷(含答案)
文档属性
| 名称 | 人教版2024—2025学年七年级下册数学期末素养检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 768.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 13:54:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2024—2025学年七年级下册数学期末素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在2025年春节联欢晚会上举行了机器人团体舞蹈表演,某中学想了解学生对此节目的喜欢情况,从全校2000名学生中随机抽取了100名学生进行调查.下列说法正确的是( )
A.本次调查方式是普查 B.2000名学生对此节目的喜欢情况是总体
C.每一名学生是总体的一个样本 D.100名学生对此节目的喜欢情况是个体
2.已知方程是关于的二元一次方程,则的值是( )
A.2 B.0或2 C.1 D.0
3.若点在第四象限,则的取值范围为( )
A. B. C. D.
4.平面直角坐标系中,将点先向右平移2个单位,再向下平移3个单位得到的点的坐标为( )
A. B. C. D.
5.下列命题中是真命题的是( )
A.相等的角是对顶角 B.同位角相等
C.两直线平行,同旁内角相等 D.如果,,那么
6.将一个含角的三角尺和直尺按如图摆放,若,则的度数是( )
B.
C. D.
7.实数,3.14,0,,,,0.1616616661,在这7个数中,无理数的个数是( )
A.5 B.4 C.3 D.2
8.已知.若为整数且,则的值为( )
A.53 B.54 C.55 D.56
9.如果关于y的方程有非负整数解,且关于x的不等式组的解集为,则所有符合条件的整数a的和为( )
A. B. C. D.
10.如图,在三角形中,,将三角形沿着射线方向平移,得到三角形,已知,则阴影部分的周长为( )
B.
C. D.
二、填空题(6小题,每题3分,共18分)
11.为了解所在小区居民各类生活垃圾的投放情况,小宇同学随机调查了该小区30户家庭某一天各类生活垃圾的投放量,统计得出这30户家庭各类生活垃圾的投放总量是70千克,各类生活垃圾投放量分布情况的扇形统计图如下图所示,若该小区有240户家庭,则可估计该小区这一天投放的可回收物共 千克.
12.若关于x,y的二元一次方程组的解满足不等式,则m的取值范围为 .
13.某种商品的进价为100元,出售时标价为125元,商店准备打折销售,但要求利润率不低于,则至多可打 折.
14.如图,直线,分别与直线交于点,.把一块含角的三角尺按如图所示的位置摆放.若,则的度数是 .
15.已知的小数部分为,的小数部分为,则 .
16.某方程组的解为,则方程组的解是 .
第II卷
人教版2024—2025学年七年级下册数学期末素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解二元二次方程组
(1);(2).
18.解不等式组:.
19.计算求值:
(1)计算:;
(2)已知(x﹣1)2﹣9=0,求x的值.
20.某校动员学生课余时间练习书法,为了了解学生们每天练习书法的情况,该校随机抽取部分学生进行问卷调查,根据调查结果绘制成如图两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(Ⅰ)本次共调查了 名学生;
(Ⅱ)在扇形统计图中,m的值是 ,20min所对应的扇形圆心角的度数是 度;
(Ⅲ)根据以上信息直接在答题卡中补全条形统计图:
(Ⅳ)根据以上调查结果,请估计该校800名学生中每天练习书法时间为25min的学生人数.
21.已知:一个正数a的两个不同平方根分别是x+5和4x﹣15.
(1)求a的值;
(2)求2a+1的立方根.
22.近期,我国国产动画电影“哪吒2魔童闹海”票房突破了90亿,商家推出A、B两种类型的哪吒纪念娃娃.已知购进4件A种娃娃和购进5件B种娃娃的费用相同;每个A种娃娃的进价比每个B种娃娃的进价多2元,且A种娃娃售价为15元/个,B种娃娃售价为10元/个.
(1)每个A种娃娃和每个B种娃娃的进价分别是多少元?
(2)根据网上预约的情况,该商家计划用不超过1700元的资金购进A、B两种娃娃共200个,若这200个娃娃全部售完,选择哪种进货方案,商家获利最大?最大利润是多少元?
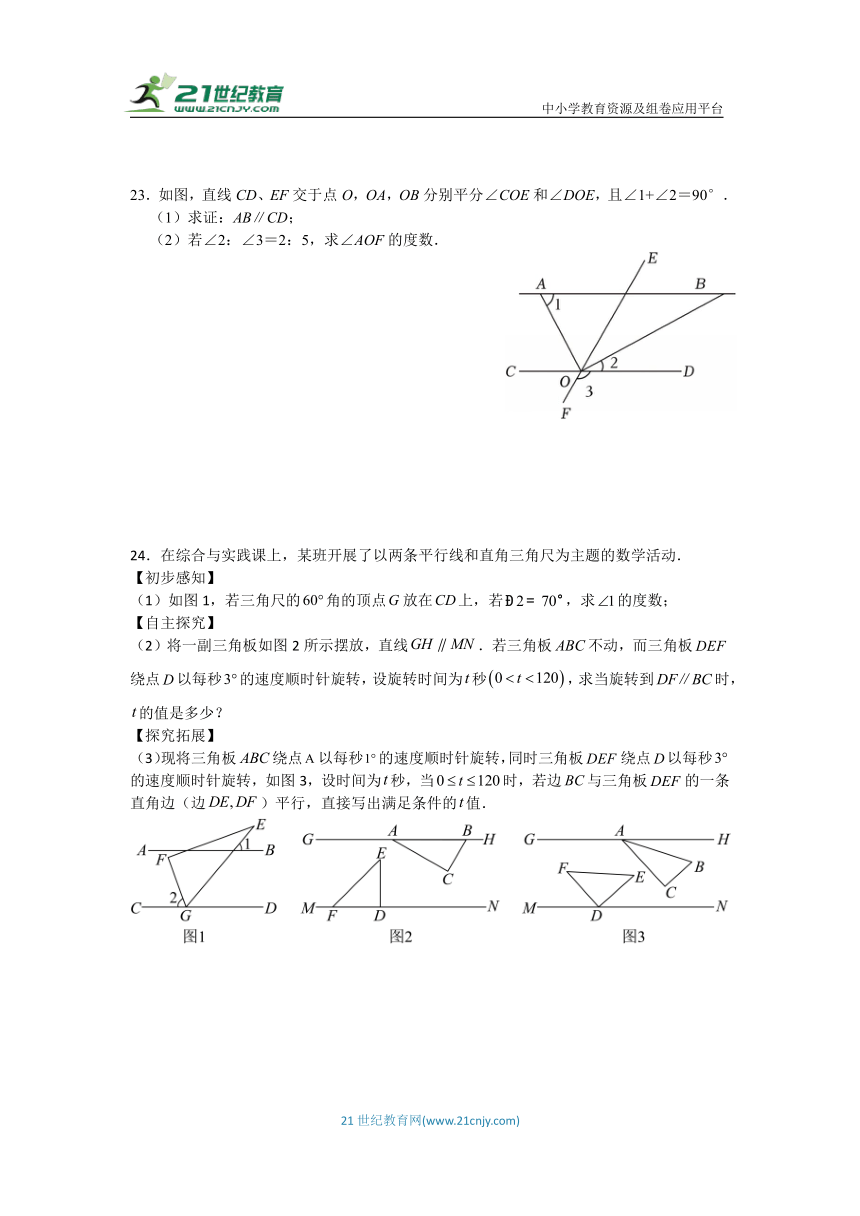
23.如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,且∠1+∠2=90°.
(1)求证:AB∥CD;
(2)若∠2:∠3=2:5,求∠AOF的度数.
24.在综合与实践课上,某班开展了以两条平行线和直角三角尺为主题的数学活动.
【初步感知】
(1)如图1,若三角尺的角的顶点放在上,若,求的度数;
【自主探究】
(2)将一副三角板如图2所示摆放,直线.若三角板不动,而三角板绕点以每秒的速度顺时针旋转,设旋转时间为秒,求当旋转到时,的值是多少?
【探究拓展】
(3)现将三角板绕点以每秒的速度顺时针旋转,同时三角板绕点以每秒的速度顺时针旋转,如图3,设时间为秒,当时,若边与三角板的一条直角边(边)平行,直接写出满足条件的值.
25.如果一个方程(组)的解恰好能够使得某不等式(组)成立,则称此方程(组)为该不等式(组)的“偏解方程(组)”、例如:方程是不等式的“偏解方程”,因为方程的解可使得成立:方程组是不等式的“偏解方程组”,因为方程组的解可使得成立.
(1)方程是下列不等式(组)中_______(填序号)的“偏解方程”;
①;②;③;
(2)已知关于,方程组是不等式的“偏解方程组”,求的取值范围;
(3)已知关于的不等式组恰有5个整数解,且关于的方程是它的“偏解方程”,求的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B D D C D B A A
二、填空题
11.【解】已知30户家庭各类生活垃圾投放总量是70千克,由扇形统计图可知可回收物占比,根据“部分量总量部分量所占百分比”,
可得30户家庭中可回收物的投放量为千克,
小区有240户家庭,30户家庭是样本,,即240户家庭是30户家庭的8倍.
那么240户家庭中可回收物的投放量为千克,
故答案为:145.6.
12.【解】解:,
①②得:,
解得:,
∵,
∴,
解得:,
故答案为:.
13.【解】解:设可打x折,
由题意得:,
解得:,
即至多可打九折.
故答案为:九.
14.【解】解:如图,
∵,,
∴,
∵,
∴,
故答案为:.
15.【解】解:∵,
∴,
∴,,
∴小数部分为,的小数部分为,
∴,,
∴.
故答案为:1.
16.【解】解:把代入程组得:
把代入得:
①-②得:,
解得:,
把代入①得:,
∴方程组的解是,
故答案为:
三、解答题
17.【解答】解:(1),
①+2×②得,13x=39,
解得,x=3,
将x=3代入①得,9+2y=9,
解得,y=0,
∴;
(2),
①×2+②得,5x=25,
解得,x=5,
将x=5代入①得,5﹣2y=1,
解得,y=2,
∴.
18.【解答】解:,
解①得x<2.5;
解②得x≥﹣1;
所以,原不等式组的解集为﹣1≤x<2.5.
19.【解答】解:(1)原式=﹣1﹣351=0;
(2)(x﹣1)2﹣9=0,
(x﹣1)2=9,
x﹣1=±3,
x1=4,x2=﹣2.
20.【解答】解:(Ⅰ)8÷16%=50(名),
故答案为:50;
(Ⅱ)16÷50×100%=32%,即m=32,
360°×=72°,
故答案为:32,72;
(Ⅲ)每天练习书法时间为10min的学生人数为:50﹣8﹣16﹣10﹣6=12(名),
补全条形统计图如下:
(Ⅳ)800×=64(人),
答:该校800名学生中每天练习书法时间为25min的学生人数大约有64人.
21.【解答】解:(1)由题意得x+5+4x﹣15=0,
解得x=2,
∴x+5=7,
∴a=(x+5)2=72=49.
(2)由(1)可知a=49,
∴2a+1=2×49+1=99,
∴2a+1的立方根为.
22.【解答】解:(1)设每个A种娃娃的进价是x元,每个B种娃娃的进价是y元,
根据题意得:,
解得:.
答:每个A种娃娃的进价是10元,每个B种娃娃的进价是8元;
(2)设购进m个A种娃娃,则购进(200﹣m)个B种娃娃,
根据题意得:10m+8(200﹣m)≤1700,
解得:m≤50.
设这200个娃娃全部售完获得的总利润为w元,则w=(15﹣10)m+(10﹣8)(200﹣m),
即w=3m+400,
∵3>0,
∴w随m的增大而增大,
∴当m=50时,w取得最大值,最大值为3×50+400=550,此时200﹣m=200﹣50=150(个).
答:当购进50个A种娃娃,150个B种娃娃时,商家获利最大,最大利润是550元.
23.【解答】(1)证明:∵OA,OB分别平分∠COE和∠DOE,
∴∠AOC∠COE,∠2∠DOE,
∵∠COE+∠DOE=180°,
∴∠AOC+∠2∠COE∠DOE=90°,
∵∠1+∠2=90°,
∴∠AOC=∠1,
∴AB∥CD;
(2)解:∵∠2:∠3=2:5,∠2∠DOE,
∴∠DOE:∠3=4:5,
∵∠DOE+∠3=180°,
∴∠DOE=180°80°,∠3=180°100°,
∴∠COE=∠3=100°,
∵OA平分∠COE,
∴∠AOE∠COE=50°,
∴∠AOF=180°﹣∠AOE=130°,
∴∠AOF的度数为130°.
24.解:(1),
.
,
,
(2)①如图所示,当在上方时,延长交于,
,
,
,
,
;
②当在下方时,只需要在旋转40秒的基础上再旋转180度即有,;
综上所述,当旋转到时,的值是40或100;
(3)①如图,当时,
设直线与分别交于,
此时,
,
,
,
,
,即,解得:;
②如图,当时,延长,分别与交于,
此时,,
,
,
,即,
,
,
解得:;
③如图所示,当时,
设直线分别交、于、,
此时,,
,
,
,,
,
.
解得.
综上:所有满足条件的的值为15或60或105.
25.(1)解:解方程得,
①不成立,故不符合题意;
②成立,故符合题意;
③成立,符合题意,
∴方程是下列不等式(组)中②③的“偏解方程”,
故答案为:②③;
(2)解:解方程组得:,
∵方程组是不等式的“偏解方程组”,
∴,
解得:;
(3)解:解不等式组得,
∵关于的方程是它的“偏解方程”,
∴,
解得:,
∴设5个整数解为,
则由题意得:,
∴,
解得:,
∵有解,
∴,
解得:,
∴的整数解为或,
①当时,,
∴;
②当时,,
∴,
∴由①②得:,
又∵,
∴.
21世纪教育网(www.21cnjy.com)
人教版2024—2025学年七年级下册数学期末素养检测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.在2025年春节联欢晚会上举行了机器人团体舞蹈表演,某中学想了解学生对此节目的喜欢情况,从全校2000名学生中随机抽取了100名学生进行调查.下列说法正确的是( )
A.本次调查方式是普查 B.2000名学生对此节目的喜欢情况是总体
C.每一名学生是总体的一个样本 D.100名学生对此节目的喜欢情况是个体
2.已知方程是关于的二元一次方程,则的值是( )
A.2 B.0或2 C.1 D.0
3.若点在第四象限,则的取值范围为( )
A. B. C. D.
4.平面直角坐标系中,将点先向右平移2个单位,再向下平移3个单位得到的点的坐标为( )
A. B. C. D.
5.下列命题中是真命题的是( )
A.相等的角是对顶角 B.同位角相等
C.两直线平行,同旁内角相等 D.如果,,那么
6.将一个含角的三角尺和直尺按如图摆放,若,则的度数是( )
B.
C. D.
7.实数,3.14,0,,,,0.1616616661,在这7个数中,无理数的个数是( )
A.5 B.4 C.3 D.2
8.已知.若为整数且,则的值为( )
A.53 B.54 C.55 D.56
9.如果关于y的方程有非负整数解,且关于x的不等式组的解集为,则所有符合条件的整数a的和为( )
A. B. C. D.
10.如图,在三角形中,,将三角形沿着射线方向平移,得到三角形,已知,则阴影部分的周长为( )
B.
C. D.
二、填空题(6小题,每题3分,共18分)
11.为了解所在小区居民各类生活垃圾的投放情况,小宇同学随机调查了该小区30户家庭某一天各类生活垃圾的投放量,统计得出这30户家庭各类生活垃圾的投放总量是70千克,各类生活垃圾投放量分布情况的扇形统计图如下图所示,若该小区有240户家庭,则可估计该小区这一天投放的可回收物共 千克.
12.若关于x,y的二元一次方程组的解满足不等式,则m的取值范围为 .
13.某种商品的进价为100元,出售时标价为125元,商店准备打折销售,但要求利润率不低于,则至多可打 折.
14.如图,直线,分别与直线交于点,.把一块含角的三角尺按如图所示的位置摆放.若,则的度数是 .
15.已知的小数部分为,的小数部分为,则 .
16.某方程组的解为,则方程组的解是 .
第II卷
人教版2024—2025学年七年级下册数学期末素养检测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解二元二次方程组
(1);(2).
18.解不等式组:.
19.计算求值:
(1)计算:;
(2)已知(x﹣1)2﹣9=0,求x的值.
20.某校动员学生课余时间练习书法,为了了解学生们每天练习书法的情况,该校随机抽取部分学生进行问卷调查,根据调查结果绘制成如图两幅不完整的统计图:
根据统计图提供的信息,解答下列问题:
(Ⅰ)本次共调查了 名学生;
(Ⅱ)在扇形统计图中,m的值是 ,20min所对应的扇形圆心角的度数是 度;
(Ⅲ)根据以上信息直接在答题卡中补全条形统计图:
(Ⅳ)根据以上调查结果,请估计该校800名学生中每天练习书法时间为25min的学生人数.
21.已知:一个正数a的两个不同平方根分别是x+5和4x﹣15.
(1)求a的值;
(2)求2a+1的立方根.
22.近期,我国国产动画电影“哪吒2魔童闹海”票房突破了90亿,商家推出A、B两种类型的哪吒纪念娃娃.已知购进4件A种娃娃和购进5件B种娃娃的费用相同;每个A种娃娃的进价比每个B种娃娃的进价多2元,且A种娃娃售价为15元/个,B种娃娃售价为10元/个.
(1)每个A种娃娃和每个B种娃娃的进价分别是多少元?
(2)根据网上预约的情况,该商家计划用不超过1700元的资金购进A、B两种娃娃共200个,若这200个娃娃全部售完,选择哪种进货方案,商家获利最大?最大利润是多少元?
23.如图,直线CD、EF交于点O,OA,OB分别平分∠COE和∠DOE,且∠1+∠2=90°.
(1)求证:AB∥CD;
(2)若∠2:∠3=2:5,求∠AOF的度数.
24.在综合与实践课上,某班开展了以两条平行线和直角三角尺为主题的数学活动.
【初步感知】
(1)如图1,若三角尺的角的顶点放在上,若,求的度数;
【自主探究】
(2)将一副三角板如图2所示摆放,直线.若三角板不动,而三角板绕点以每秒的速度顺时针旋转,设旋转时间为秒,求当旋转到时,的值是多少?
【探究拓展】
(3)现将三角板绕点以每秒的速度顺时针旋转,同时三角板绕点以每秒的速度顺时针旋转,如图3,设时间为秒,当时,若边与三角板的一条直角边(边)平行,直接写出满足条件的值.
25.如果一个方程(组)的解恰好能够使得某不等式(组)成立,则称此方程(组)为该不等式(组)的“偏解方程(组)”、例如:方程是不等式的“偏解方程”,因为方程的解可使得成立:方程组是不等式的“偏解方程组”,因为方程组的解可使得成立.
(1)方程是下列不等式(组)中_______(填序号)的“偏解方程”;
①;②;③;
(2)已知关于,方程组是不等式的“偏解方程组”,求的取值范围;
(3)已知关于的不等式组恰有5个整数解,且关于的方程是它的“偏解方程”,求的取值范围.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B D D C D B A A
二、填空题
11.【解】已知30户家庭各类生活垃圾投放总量是70千克,由扇形统计图可知可回收物占比,根据“部分量总量部分量所占百分比”,
可得30户家庭中可回收物的投放量为千克,
小区有240户家庭,30户家庭是样本,,即240户家庭是30户家庭的8倍.
那么240户家庭中可回收物的投放量为千克,
故答案为:145.6.
12.【解】解:,
①②得:,
解得:,
∵,
∴,
解得:,
故答案为:.
13.【解】解:设可打x折,
由题意得:,
解得:,
即至多可打九折.
故答案为:九.
14.【解】解:如图,
∵,,
∴,
∵,
∴,
故答案为:.
15.【解】解:∵,
∴,
∴,,
∴小数部分为,的小数部分为,
∴,,
∴.
故答案为:1.
16.【解】解:把代入程组得:
把代入得:
①-②得:,
解得:,
把代入①得:,
∴方程组的解是,
故答案为:
三、解答题
17.【解答】解:(1),
①+2×②得,13x=39,
解得,x=3,
将x=3代入①得,9+2y=9,
解得,y=0,
∴;
(2),
①×2+②得,5x=25,
解得,x=5,
将x=5代入①得,5﹣2y=1,
解得,y=2,
∴.
18.【解答】解:,
解①得x<2.5;
解②得x≥﹣1;
所以,原不等式组的解集为﹣1≤x<2.5.
19.【解答】解:(1)原式=﹣1﹣351=0;
(2)(x﹣1)2﹣9=0,
(x﹣1)2=9,
x﹣1=±3,
x1=4,x2=﹣2.
20.【解答】解:(Ⅰ)8÷16%=50(名),
故答案为:50;
(Ⅱ)16÷50×100%=32%,即m=32,
360°×=72°,
故答案为:32,72;
(Ⅲ)每天练习书法时间为10min的学生人数为:50﹣8﹣16﹣10﹣6=12(名),
补全条形统计图如下:
(Ⅳ)800×=64(人),
答:该校800名学生中每天练习书法时间为25min的学生人数大约有64人.
21.【解答】解:(1)由题意得x+5+4x﹣15=0,
解得x=2,
∴x+5=7,
∴a=(x+5)2=72=49.
(2)由(1)可知a=49,
∴2a+1=2×49+1=99,
∴2a+1的立方根为.
22.【解答】解:(1)设每个A种娃娃的进价是x元,每个B种娃娃的进价是y元,
根据题意得:,
解得:.
答:每个A种娃娃的进价是10元,每个B种娃娃的进价是8元;
(2)设购进m个A种娃娃,则购进(200﹣m)个B种娃娃,
根据题意得:10m+8(200﹣m)≤1700,
解得:m≤50.
设这200个娃娃全部售完获得的总利润为w元,则w=(15﹣10)m+(10﹣8)(200﹣m),
即w=3m+400,
∵3>0,
∴w随m的增大而增大,
∴当m=50时,w取得最大值,最大值为3×50+400=550,此时200﹣m=200﹣50=150(个).
答:当购进50个A种娃娃,150个B种娃娃时,商家获利最大,最大利润是550元.
23.【解答】(1)证明:∵OA,OB分别平分∠COE和∠DOE,
∴∠AOC∠COE,∠2∠DOE,
∵∠COE+∠DOE=180°,
∴∠AOC+∠2∠COE∠DOE=90°,
∵∠1+∠2=90°,
∴∠AOC=∠1,
∴AB∥CD;
(2)解:∵∠2:∠3=2:5,∠2∠DOE,
∴∠DOE:∠3=4:5,
∵∠DOE+∠3=180°,
∴∠DOE=180°80°,∠3=180°100°,
∴∠COE=∠3=100°,
∵OA平分∠COE,
∴∠AOE∠COE=50°,
∴∠AOF=180°﹣∠AOE=130°,
∴∠AOF的度数为130°.
24.解:(1),
.
,
,
(2)①如图所示,当在上方时,延长交于,
,
,
,
,
;
②当在下方时,只需要在旋转40秒的基础上再旋转180度即有,;
综上所述,当旋转到时,的值是40或100;
(3)①如图,当时,
设直线与分别交于,
此时,
,
,
,
,
,即,解得:;
②如图,当时,延长,分别与交于,
此时,,
,
,
,即,
,
,
解得:;
③如图所示,当时,
设直线分别交、于、,
此时,,
,
,
,,
,
.
解得.
综上:所有满足条件的的值为15或60或105.
25.(1)解:解方程得,
①不成立,故不符合题意;
②成立,故符合题意;
③成立,符合题意,
∴方程是下列不等式(组)中②③的“偏解方程”,
故答案为:②③;
(2)解:解方程组得:,
∵方程组是不等式的“偏解方程组”,
∴,
解得:;
(3)解:解不等式组得,
∵关于的方程是它的“偏解方程”,
∴,
解得:,
∴设5个整数解为,
则由题意得:,
∴,
解得:,
∵有解,
∴,
解得:,
∴的整数解为或,
①当时,,
∴;
②当时,,
∴,
∴由①②得:,
又∵,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
