上海市黄浦区2010届高三上学期期终基础学业测评(数学文)
文档属性
| 名称 | 上海市黄浦区2010届高三上学期期终基础学业测评(数学文) |

|
|
| 格式 | zip | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
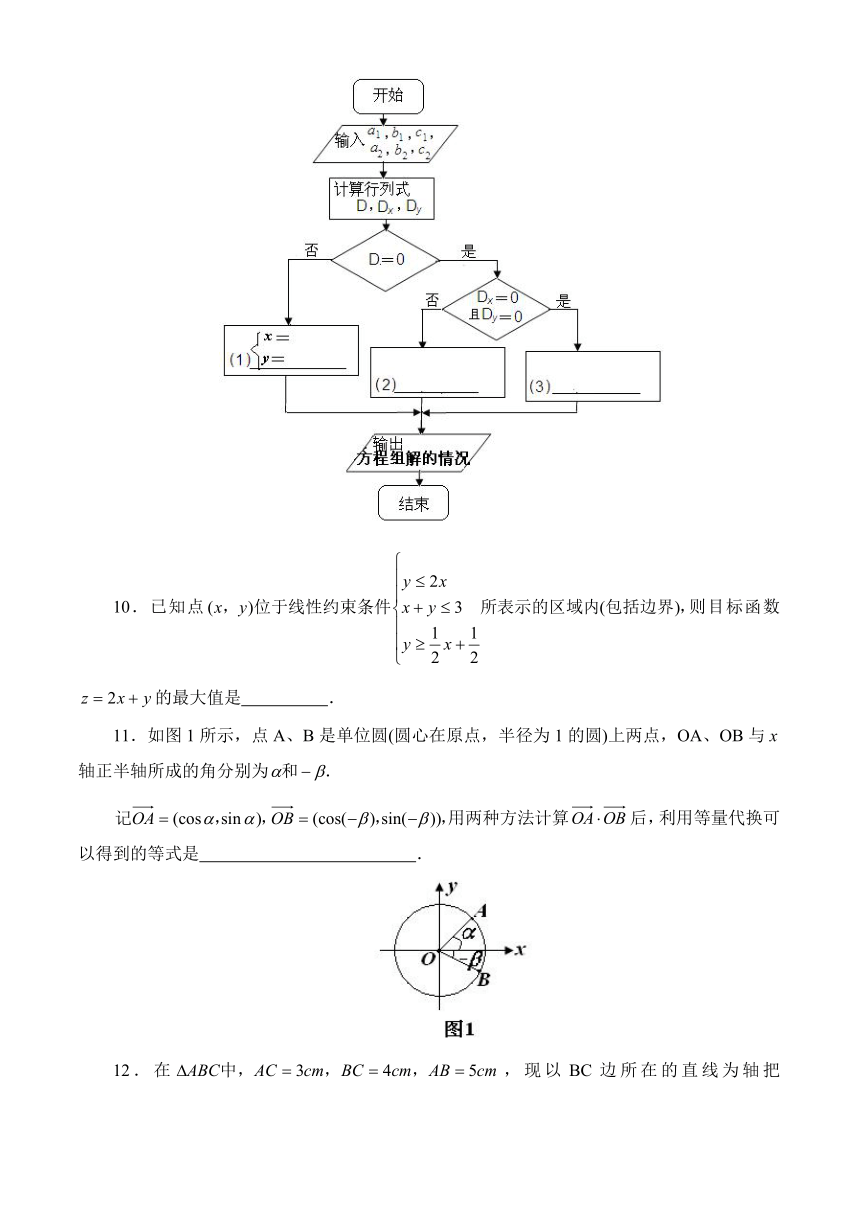
| 科目 | 数学 | ||
| 更新时间 | 2010-02-02 00:00:00 | ||
图片预览



文档简介
上海市黄浦区2010届高三上学期期终基础学业测评
高三数学试卷(文科) (2010.1.20)
考生注意:
1.每位考生应同时收到试卷和答题卷两份材料,解答必须在答题卷上进行,写在试卷上的解答一律无效;
2.答卷前,考生务必将姓名、准考证号等相关信息在答题卷上填写清楚;
3.本试卷共23道试题,满分150分;考试时间120分钟.
命题人:王新新 审核:雷锋瑞 校对:刘超
一.填空题(本大题满分56分) 本大题共有14题,考生应在答题卷的相应编号的空格内直接填写结果,每题填对得4分,否则一律得零分.
1.已知函数的图像上,则实数 .
2.平行,则a、b满足的条件是 .
3.不等式的解集是 .
4.已知角的顶点在原点,始边与x轴正半轴重合,点P是角终边上一点,则= .
5.方程的解集是 .
6.方程的解 .
7. .
8. .
9.下面是用行列式解二元一次方程组的程序框图,请在(1)、(2)、(3)处分别填上合适的指令.
10.已知点则目标函数的最大值是 .
11.如图1所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为
用两种方法计算后,利用等量代换可以得到的等式是 .
12.在,现以BC边所在的直线为轴把(及其内部)旋转一周后,所得几何体的全面积是 .
13.掷一枚质地均匀的硬币可能出现图案向上,也可能出现文字向上.现将一枚质地均匀的硬币连续掷3次,记A表示 “3次中出现2次图案向上” 的事件= .
14.给出下列4个命题,其中正确命题的序号是 .
(1)在大量的试验中,事件A出现的频率可作为事件A出现的概率的估计值;
(2)样本标准差可作为总体标准差的点估计值;
(3)随机抽样就是使得总体中每一个个体都有同样的可能性被选入样本的一种抽样方法;
(4)分层抽样就是把总体分成若干部分,然后在每个部分指定某些个体作为样本的一种抽样方法.
二.选择题(本大题满分16分) 本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得4分,否则一律得零分.
15.已知 [答]( )
A.充要条件. B.充分非必要条件.
C.必要非充分条件. D.非充分非必要条件.
16.定义两种运算的解析式是 [答]( )
A.. B..
C..
D..
17.在空间中,给出下列4个命题(其中表示直线,表示平面),则正确命题的序号是 [答]( )
(1)三个点确定一个平面;
(2)若
(3)在空间中,若角的两边分别平行,则;
(4)若.
A.(1)、(2)、(4). B.(2). C.(2)、(3). D.(2)、(3)、(4).
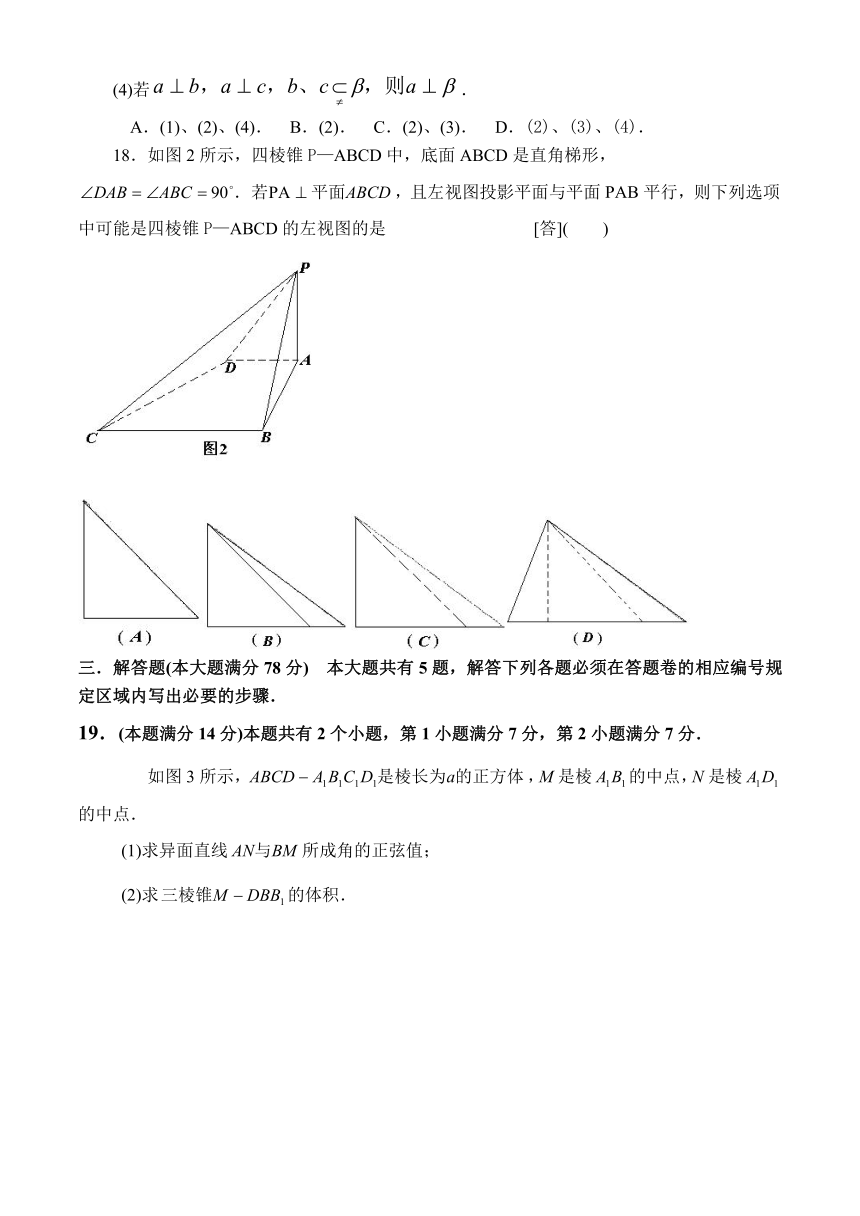
18.如图2所示,四棱锥P—ABCD中,底面ABCD是直角梯形,
,且左视图投影平面与平面PAB平行,则下列选项中可能是四棱锥P—ABCD的左视图的是 [答]( )
三.解答题(本大题满分78分) 本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤.
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
如图3所示,,M是棱的中点,N是棱的中点.
(1)求异面直线所成角的正弦值;
(2)求的体积.
20.(本题满分14分)
21.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知a、b是正整数,函数的图像经过点.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在上的单调性,并用单调性定义证明你的结论.
22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x万件与年促销费用t万元之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(1)求出x与t所满足的关系式;
(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;
(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
(其中A、B是常数,).
(1)求A、B的值;
(2)求证;
(3)已知k是正整数,不等式求k的最小值.
黄浦区2009学年度第一学期期末教学质量检测
数学试卷(文科)(2010年1月20日)
参考答案和评分标准
说明:
1、本解答仅列出试题的一种解法,如果考生的解法与所列解答不同,可参考解答中的评分精神进行评分。
2、评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
一、填空题
1、 8、
2、 9、(1)2分、(2)方程组无解1分、(3)方程组有无穷多解1分
3、 10、
4、 11、
5、 12、
6、 13、
7、2 14、(1)、(2)、(3)
二、选择题: 15、C 16、B 17、B 18、A
三、解答题
19、(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
解 (1),GM与的交点为H,联结BH,如图所示.……………………………………………………1分
∵是正方体,G、N是中点,
∴,即ABGN为平行四边形.
∴BG||AN,所成的角.
……………………………………………………3分
又正方体的棱长为a,可得,
.∴. ……………6分
∴.…………………………………………………………………7分
(2)∵
∴.………9分
∵,
∴.
∴的高.…………………………12分
∴
=
=. …………………………………………………14分
20.(本题满分14分)
解
.……… ………………3分
,
,,解得.…… …………………8分
由……………………………10分
∴,. ……………… ………………………………………13分
. ……………………… ……………………………………14分
21.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
解 (1) 由函数,知
.……………………………………………2分
又,
故.于是,必有 .………………7分
所以.………………………………………………8分
(2) 结论:上是减函数.……………………9分
证明 设.………………10分
则………………………………11分
=
=.………………………………13分
又.14分
于是,,即.……16分
所以,函数上是减函数.
22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
解 (1) 设比例系数为k.由题知,有.………………………2分
又
.……………………………………………………………4分
.…………………… ………………………5分
(2) 依据题意,可知工厂生产x万件纪念品的生产成本为万元,促销费用为t万元,则每件纪念品的定价为:()元/件.…………………………8分
于是,,进一步化简,得
.……………………………………………… ……………11分
因此,工厂2010年的年利润万元.
(3) 由(2)知,
……………15分
所以,当2010年的促销费用投入7万元时,工厂的年利润最大,最大利润为42万元.…………………………………………………………………………… ……………16分
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
解 (1),
分别取n=1和n=2,得,……………………………………3分
即,解得.…………………………………………………6分
证明 (2)由(1)知,,
∴.两式相差,得
,即.………………………8分
两边同除以,可化为
.………………………………10分
∴.…11分
∴.………………………………………12分
(3) 由(2)知,.又,即,进一步可化为.………………………………………………………………14分
当,…………………………………… ……16分
因此,只要即满足要求.又k是正整数,故所求k的最小值为32.…… ……18分
高三数学试卷(文科) (2010.1.20)
考生注意:
1.每位考生应同时收到试卷和答题卷两份材料,解答必须在答题卷上进行,写在试卷上的解答一律无效;
2.答卷前,考生务必将姓名、准考证号等相关信息在答题卷上填写清楚;
3.本试卷共23道试题,满分150分;考试时间120分钟.
命题人:王新新 审核:雷锋瑞 校对:刘超
一.填空题(本大题满分56分) 本大题共有14题,考生应在答题卷的相应编号的空格内直接填写结果,每题填对得4分,否则一律得零分.
1.已知函数的图像上,则实数 .
2.平行,则a、b满足的条件是 .
3.不等式的解集是 .
4.已知角的顶点在原点,始边与x轴正半轴重合,点P是角终边上一点,则= .
5.方程的解集是 .
6.方程的解 .
7. .
8. .
9.下面是用行列式解二元一次方程组的程序框图,请在(1)、(2)、(3)处分别填上合适的指令.
10.已知点则目标函数的最大值是 .
11.如图1所示,点A、B是单位圆(圆心在原点,半径为1的圆)上两点,OA、OB与x轴正半轴所成的角分别为
用两种方法计算后,利用等量代换可以得到的等式是 .
12.在,现以BC边所在的直线为轴把(及其内部)旋转一周后,所得几何体的全面积是 .
13.掷一枚质地均匀的硬币可能出现图案向上,也可能出现文字向上.现将一枚质地均匀的硬币连续掷3次,记A表示 “3次中出现2次图案向上” 的事件= .
14.给出下列4个命题,其中正确命题的序号是 .
(1)在大量的试验中,事件A出现的频率可作为事件A出现的概率的估计值;
(2)样本标准差可作为总体标准差的点估计值;
(3)随机抽样就是使得总体中每一个个体都有同样的可能性被选入样本的一种抽样方法;
(4)分层抽样就是把总体分成若干部分,然后在每个部分指定某些个体作为样本的一种抽样方法.
二.选择题(本大题满分16分) 本大题共有4题,每题有且只有一个正确答案,考生应在答题卷的相应编号上,将代表答案的小方格涂黑,选对得4分,否则一律得零分.
15.已知 [答]( )
A.充要条件. B.充分非必要条件.
C.必要非充分条件. D.非充分非必要条件.
16.定义两种运算的解析式是 [答]( )
A.. B..
C..
D..
17.在空间中,给出下列4个命题(其中表示直线,表示平面),则正确命题的序号是 [答]( )
(1)三个点确定一个平面;
(2)若
(3)在空间中,若角的两边分别平行,则;
(4)若.
A.(1)、(2)、(4). B.(2). C.(2)、(3). D.(2)、(3)、(4).
18.如图2所示,四棱锥P—ABCD中,底面ABCD是直角梯形,
,且左视图投影平面与平面PAB平行,则下列选项中可能是四棱锥P—ABCD的左视图的是 [答]( )
三.解答题(本大题满分78分) 本大题共有5题,解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤.
19.(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
如图3所示,,M是棱的中点,N是棱的中点.
(1)求异面直线所成角的正弦值;
(2)求的体积.
20.(本题满分14分)
21.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
已知a、b是正整数,函数的图像经过点.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在上的单调性,并用单调性定义证明你的结论.
22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
某生产旅游纪念品的工厂,拟在2010年度将进行系列促销活动.经市场调查和测算,该纪念品的年销售量x万件与年促销费用t万元之间满足3-x与t+1成反比例.若不搞促销活动,纪念品的年销售量只有1万件.已知工厂2010年生产纪念品的固定投资为3万元,每生产1万件纪念品另外需要投资32万元.当工厂把每件纪念品的售价定为:“年平均每件生产成本的150%”与“年平均每件所占促销费一半”之和时,则当年的产量和销量相等.(利润=收入-生产成本-促销费用)
(1)求出x与t所满足的关系式;
(2)请把该工厂2010年的年利润y万元表示成促销费t万元的函数;
(3)试问:当2010年的促销费投入多少万元时,该工厂的年利润最大?
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
(其中A、B是常数,).
(1)求A、B的值;
(2)求证;
(3)已知k是正整数,不等式求k的最小值.
黄浦区2009学年度第一学期期末教学质量检测
数学试卷(文科)(2010年1月20日)
参考答案和评分标准
说明:
1、本解答仅列出试题的一种解法,如果考生的解法与所列解答不同,可参考解答中的评分精神进行评分。
2、评阅试卷,应坚持每题评阅到底,不要因为考生的解答中出现错误而中断对该题的评阅,当考生的解答在某一步出现错误,影响了后继部分,但该步以后的解答未改变这一题的内容和难度时,可视影响程度决定后面部分的给分,这时原则上不应超过后面部分应给分数之半,如果有较严重的概念性错误,就不给分。
一、填空题
1、 8、
2、 9、(1)2分、(2)方程组无解1分、(3)方程组有无穷多解1分
3、 10、
4、 11、
5、 12、
6、 13、
7、2 14、(1)、(2)、(3)
二、选择题: 15、C 16、B 17、B 18、A
三、解答题
19、(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
解 (1),GM与的交点为H,联结BH,如图所示.……………………………………………………1分
∵是正方体,G、N是中点,
∴,即ABGN为平行四边形.
∴BG||AN,所成的角.
……………………………………………………3分
又正方体的棱长为a,可得,
.∴. ……………6分
∴.…………………………………………………………………7分
(2)∵
∴.………9分
∵,
∴.
∴的高.…………………………12分
∴
=
=. …………………………………………………14分
20.(本题满分14分)
解
.……… ………………3分
,
,,解得.…… …………………8分
由……………………………10分
∴,. ……………… ………………………………………13分
. ……………………… ……………………………………14分
21.(本题满分16分)本题共有2个小题,第1小题满分8分,第2小题满分8分.
解 (1) 由函数,知
.……………………………………………2分
又,
故.于是,必有 .………………7分
所以.………………………………………………8分
(2) 结论:上是减函数.……………………9分
证明 设.………………10分
则………………………………11分
=
=.………………………………13分
又.14分
于是,,即.……16分
所以,函数上是减函数.
22.(本题满分16分)本题共有3个小题,第1小题满分5分,第2小题满分6分,第3小题满分5分.
解 (1) 设比例系数为k.由题知,有.………………………2分
又
.……………………………………………………………4分
.…………………… ………………………5分
(2) 依据题意,可知工厂生产x万件纪念品的生产成本为万元,促销费用为t万元,则每件纪念品的定价为:()元/件.…………………………8分
于是,,进一步化简,得
.……………………………………………… ……………11分
因此,工厂2010年的年利润万元.
(3) 由(2)知,
……………15分
所以,当2010年的促销费用投入7万元时,工厂的年利润最大,最大利润为42万元.…………………………………………………………………………… ……………16分
23.(本题满分18分)本题共有3个小题,第1小题满分6分,第2小题满分6分,第3小题满分6分.
解 (1),
分别取n=1和n=2,得,……………………………………3分
即,解得.…………………………………………………6分
证明 (2)由(1)知,,
∴.两式相差,得
,即.………………………8分
两边同除以,可化为
.………………………………10分
∴.…11分
∴.………………………………………12分
(3) 由(2)知,.又,即,进一步可化为.………………………………………………………………14分
当,…………………………………… ……16分
因此,只要即满足要求.又k是正整数,故所求k的最小值为32.…… ……18分
同课章节目录
