青岛版2024—2025学年七年级下册数学期末考试押题预测卷(含答案)
文档属性
| 名称 | 青岛版2024—2025学年七年级下册数学期末考试押题预测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 12:48:06 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
青岛版2024—2025学年七年级下册数学期末考试押题预测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若要调查下列问题,你认为适合采用全面调查的是( )
A.对全国中学生每天睡眠时长情况的调查
B.对一批节能灯的使用寿命的调查
C.对北仑区城湾水库水质情况的调查
D.对载人航天飞船发射前各零部件质量情况的调查
2.如图,下列条件能判定的是( )
A. B. C. D.
3.期中考试后,老师计划购买笔记本和圆珠笔给表现优秀的同学作为奖品,笔记本和圆珠笔的单价均为正整数.若购买3本笔记本,5支圆珠笔,共需要23元,则购买4本笔记本和5支圆珠笔的费用为( )
A.24元或29元 B.29元 C.34元或21元 D.24元
4.关于的方程组与有相同的解,则的值为( )
A. B. C. D.
5.请看杨辉三角(如图),并观察下列等式:
根据前面各式的规律,则的第三项系数是( )
A.730 B.741 C.780 D.820
6.一个多项式因式分解后的一个因式为,这个多项式可能是( )
A. B. C. D.
7.如图1是化学实验中利用酒精灯给试管中液体加热的实验装置图,如图2是其简化示意图.若,则的度数为( )
A. B. C. D.
8.如图,已知直线与正六边形的边分别相交于点M,N,则( )
A. B. C. D.
9.已知,,,则下列结论错误的是( )
A. B. C. D.
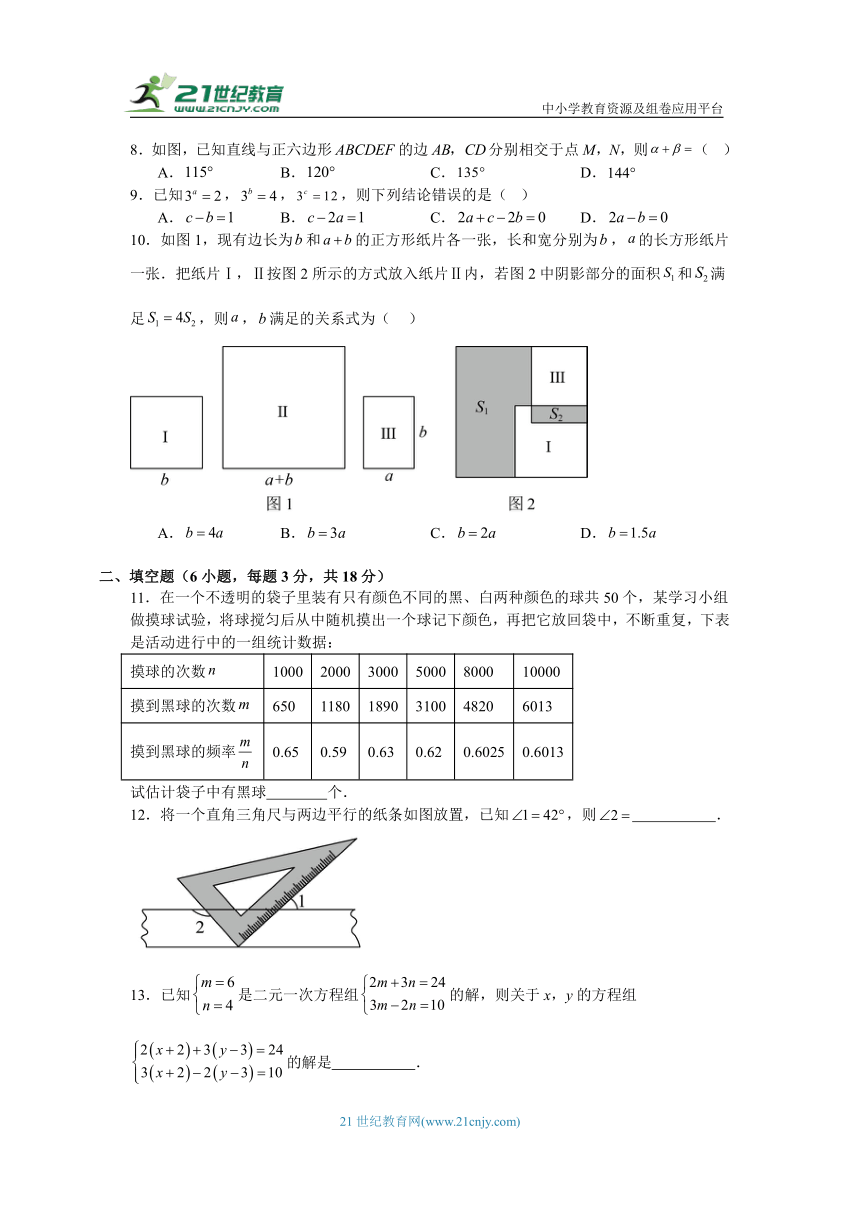
10.如图1,现有边长为和的正方形纸片各一张,长和宽分别为,的长方形纸片一张.把纸片Ⅰ,Ⅱ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积和满足,则,满足的关系式为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数 1000 2000 3000 5000 8000 10000
摸到黑球的次数 650 1180 1890 3100 4820 6013
摸到黑球的频率 0.65 0.59 0.63 0.62 0.6025 0.6013
试估计袋子中有黑球 个.
12.将一个直角三角尺与两边平行的纸条如图放置,已知,则 .
13.已知是二元一次方程组的解,则关于x,y的方程组的解是 .
14.如果与的乘积中不含的一次项,则的值为 .
15.若一个三位正整数P可以分解成的形式(其中均为正整数且,则称P 为“平方差分解数”.在的所有分解中,当取得最小值时,称为的最优分解,此时规定:.计算 ;若三位数为“平方差分解数”,其中,,均为整数,,,,且的个位数字与十位数字相同,将的各个数位上的数字之和记为,记,若为的整数倍,为满足条件的所有三位整数中的最小值,则
16.如图,直线,点E、F分别在上,连接,的平分线与直线交于点G.有一个动点M在射线上运动(不与点E、点G重合),连接,若,则 .
青岛版2024—2025学年七年级下册数学期末考试押题预测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列一元一次方程组:
(1) (2)
18.若关于的方程组与方程组的解相同.
(1)求两个方程组的相同解;
(2)求的值.
19.先化简再求值:,其中.
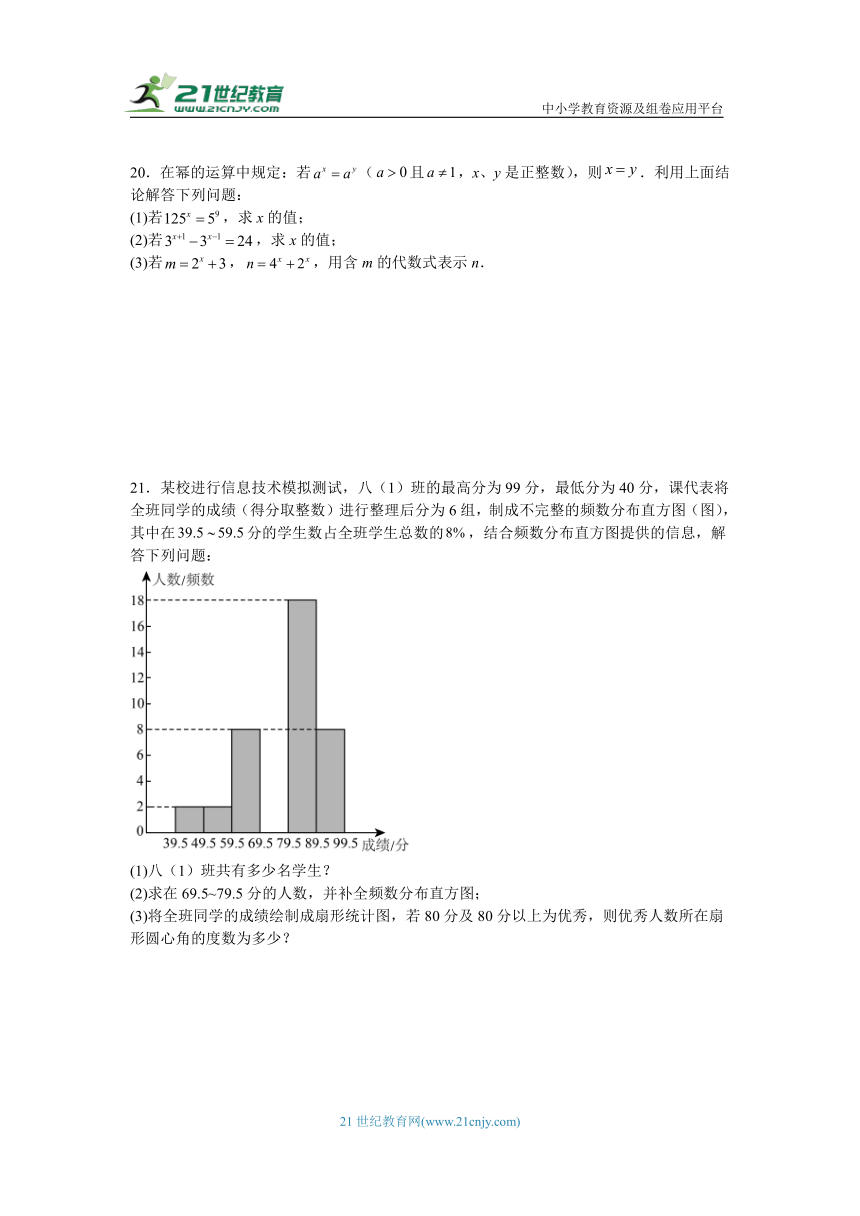
20.在幂的运算中规定:若(且,x、y是正整数),则.利用上面结论解答下列问题:
(1)若,求x的值;
(2)若,求x的值;
(3)若,,用含m的代数式表示n.
21.某校进行信息技术模拟测试,八(1)班的最高分为99分,最低分为40分,课代表将全班同学的成绩(得分取整数)进行整理后分为6组,制成不完整的频数分布直方图(图),其中在分的学生数占全班学生总数的,结合频数分布直方图提供的信息,解答下列问题:
(1)八(1)班共有多少名学生?
(2)求在69.5~79.5分的人数,并补全频数分布直方图;
(3)将全班同学的成绩绘制成扇形统计图,若80分及80分以上为优秀,则优秀人数所在扇形圆心角的度数为多少?
22.如图,已知,直线交于点,交于点,是线段上一动点(不与点重合).
(1)若,求的度数;
(2)若,求与的度数之和(用含的代数式表示).
23.字水中学十分重视培养学生的综合素质,组织七年级学生参加研学活动,需租用两种不同型号的客车,每辆座位如下表:若租用型客车5辆和型客车2辆,则需要租金2500元;若租用型客车1辆和型客车5辆,则需要租金2800元.
客车型号
人数/辆 30 45
(1)求租用、两种型号客车,每辆车租金分别是多少元?
(2)现有七年级师生450人,现计划同时租用两种型号客车,一次送完,且恰好每辆车都坐满,有几种租车方案?为节约成本,则租用A型客车和B型客车各多少辆,需要花费多少钱?
24.在数学学习中,通常用两种不同的方法计算同一个图形的面积,可以得到一个恒等式,充分体现了数形结合的思想方法.如图,用图1三种不同大小的正方形与长方形若干个,可以拼成一个如图2所示的正方形.
(1)观察猜想:观察图2,用两种不同的方法表示图2阴影部分的面积则可得,,之间的数量关系为:______;
(2)理解运用:若,,根据(1)中得出的数量关系,求,的值;
(3)拓展提升:若满足,求的值.
25.已知,点、分别在直线、上,点在、之间,连接、,设,(、均小于).
(1)如图1,试说明.
(2)点是下方一点,连接,线段与射线交于点.
①如图2,当点在线段上时,若,求的度数(结果用含的代数式表示);
②如图3,当点在线段延长线上时,若平分平分,,求的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A D C A B B C C
二、填空题
11.【解】解:由表可知,当n很大时,摸到黑球的频率将会接近,
所以黑球的个数约为个,
故答案为:.
12.【解】解:如图所示,∵,
∴,
∵,
∴,
∴,
故答案为:.
13.【解】解:令,,则关于,的方程组可转化为.
是的解,
.
解,得;解,得.
故答案为: .
14.【解】解:
,
∵与的乘积中不含的一次项,
,解得,.
故答案为:.
15.【解】解:∵120 是平方差分解数,即 对于正整数 .
根据平方差公式,.
设 ,,则 ,且 , 和 同奇偶(因为 , 需为整数)
120 的因子对及同奇偶检查:
经检验,有效数对为 、、、.
最小 为 2(对应 ).
此时,,.
验证:.
最优分解为 ,.
则:
∵ 是三位数,其中 ,,( 隐含为整数且 ,因 为三位数).
∵个位数字与十位数字相同.设十位和个位数字均为 ,则 .由 ,得:
即 被 11 整除.
设 ( 为整数,),则:,为整数,
又∵,余数为 5
所以 .为整数,
的可能 值为:17, 28, 39, 50, 61, 72, 83, 94.
经检验,∶ ,,.
∶ ,,.
∶ ,,.
数字和 .
∵, 为 5 的整数倍.
恒成立.
为整数,故 整除 10,且 (因 ).
10 的因子 ∶ 5, 10.
所以 或 ,即 或 .
若 ,∶
需为 5 的倍数:
()∶ (不满足).
()∶ (满足).
()∶ (不满足).
所以 ,,.
若 ,∶
需为 5 的倍数:
()∶ (不满足).
()∶ (不满足).
()∶ (满足).
所以 ,,.
可能 值:388 和 899.
需为平方差分解数:
∶ 分解为 .
经检验有效数对为:.
,.
验证:,最小 .是平方差分解数.
∶ 分解为 .
因子对:(同奇),(同奇).
最小 (对应 ):
,.
验证:.是平方差分解数.
满足条件的 中最小值为 388(因 ).
最优分解为 ,.
则:
∴
故答案为:,.
16.【解】解:设,,
,
,
若点M在直线上方时,如图,
,
若点M在直线与之间时,如图,
综上所述或,
故答案为:或.
三、解答题
17.【解】(1)解:
①+②,得
将代入①,得,
∴原方程组的解为.
(2)解:
方程组整理为:
,得,
解得,
将代入②,得,
∴原方程组的解为.
18.【解】(1)解:两方程组化简可得,,
∵两方程组同解,
∴,
得:,
解得:,
把代入①式得:,
∴两个方程组的相同解为;
(2)解:把代入方程组可得:
,
式得:,
解得:,
把代入②式得:,
∴.
19.【解】解:.
当时,
原式.
20.【解】(1)解:∵,
∴.
∵,即.
根据(且,、是正整数),则,
∴,
解得.
(2)解:∵,.
∴.
∵,
∴,,,,
∴.
(3)解:∵, ,
∴.
又∵,
∴把代入,得.
21.【解】(1)解:(人),
答:八(1)班共有50名学生;
(2)解:的人数为(人),
补全图形如下:
;
(3)解:
答:优秀人数所在扇形圆心角的度数为.
22.【解】(1)解:过点作,而,
则,
∴
∵ ,
∴ ,
∴.
(2)解:由(1)知,
∵ ,
∴ ,
∴,
∴.
23.【解】(1)解:设租用A、B两种型号客车,每辆车租金分别是、元,
由题意得:,解得:,
答:租用A、B两种型号客车,每辆车租金分别是、元;
(2)解:设租用A型客车辆,租用B型客车辆,
则,
则,
、都是正整数,
当时,,此时租车费用为(元);
当时,,此时租车费用为(元);
当时,,此时租车费用为(元);
当时,,此时租车费用为(元);
则为了节约成本,则租用A型客车辆,租用B型客车辆,需要花费元.
24.【解】(1)解:由图2可得,阴影部分的面积等于两个小正方形的面积之和,即为;
阴影部分的面积也等于大正方形的面积减去两个长方的面积,即,
,
故答案为:;
(2)解:∵,
,
解得:,
,
,
,
.
(3)解:设,
,
由(2)知,,
,
,
即.
25.【解】(1)解:过点作,
∵,
∴,
∴,,
∴;
(2)解:①∵,,,
∴,,
∵,
∴,
∴;
②过点作,
∵,
∴,
∴,,
∵平分,
∴,
∵平分,
∴,,
∵,
∴,
∵,
∴,
∵,
又由(1)知:,
∴,
∴,
∴.
21世纪教育网(www.21cnjy.com)
青岛版2024—2025学年七年级下册数学期末考试押题预测卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.若要调查下列问题,你认为适合采用全面调查的是( )
A.对全国中学生每天睡眠时长情况的调查
B.对一批节能灯的使用寿命的调查
C.对北仑区城湾水库水质情况的调查
D.对载人航天飞船发射前各零部件质量情况的调查
2.如图,下列条件能判定的是( )
A. B. C. D.
3.期中考试后,老师计划购买笔记本和圆珠笔给表现优秀的同学作为奖品,笔记本和圆珠笔的单价均为正整数.若购买3本笔记本,5支圆珠笔,共需要23元,则购买4本笔记本和5支圆珠笔的费用为( )
A.24元或29元 B.29元 C.34元或21元 D.24元
4.关于的方程组与有相同的解,则的值为( )
A. B. C. D.
5.请看杨辉三角(如图),并观察下列等式:
根据前面各式的规律,则的第三项系数是( )
A.730 B.741 C.780 D.820
6.一个多项式因式分解后的一个因式为,这个多项式可能是( )
A. B. C. D.
7.如图1是化学实验中利用酒精灯给试管中液体加热的实验装置图,如图2是其简化示意图.若,则的度数为( )
A. B. C. D.
8.如图,已知直线与正六边形的边分别相交于点M,N,则( )
A. B. C. D.
9.已知,,,则下列结论错误的是( )
A. B. C. D.
10.如图1,现有边长为和的正方形纸片各一张,长和宽分别为,的长方形纸片一张.把纸片Ⅰ,Ⅱ按图2所示的方式放入纸片Ⅱ内,若图2中阴影部分的面积和满足,则,满足的关系式为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.在一个不透明的袋子里装有只有颜色不同的黑、白两种颜色的球共50个,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
摸球的次数 1000 2000 3000 5000 8000 10000
摸到黑球的次数 650 1180 1890 3100 4820 6013
摸到黑球的频率 0.65 0.59 0.63 0.62 0.6025 0.6013
试估计袋子中有黑球 个.
12.将一个直角三角尺与两边平行的纸条如图放置,已知,则 .
13.已知是二元一次方程组的解,则关于x,y的方程组的解是 .
14.如果与的乘积中不含的一次项,则的值为 .
15.若一个三位正整数P可以分解成的形式(其中均为正整数且,则称P 为“平方差分解数”.在的所有分解中,当取得最小值时,称为的最优分解,此时规定:.计算 ;若三位数为“平方差分解数”,其中,,均为整数,,,,且的个位数字与十位数字相同,将的各个数位上的数字之和记为,记,若为的整数倍,为满足条件的所有三位整数中的最小值,则
16.如图,直线,点E、F分别在上,连接,的平分线与直线交于点G.有一个动点M在射线上运动(不与点E、点G重合),连接,若,则 .
青岛版2024—2025学年七年级下册数学期末考试押题预测卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.解下列一元一次方程组:
(1) (2)
18.若关于的方程组与方程组的解相同.
(1)求两个方程组的相同解;
(2)求的值.
19.先化简再求值:,其中.
20.在幂的运算中规定:若(且,x、y是正整数),则.利用上面结论解答下列问题:
(1)若,求x的值;
(2)若,求x的值;
(3)若,,用含m的代数式表示n.
21.某校进行信息技术模拟测试,八(1)班的最高分为99分,最低分为40分,课代表将全班同学的成绩(得分取整数)进行整理后分为6组,制成不完整的频数分布直方图(图),其中在分的学生数占全班学生总数的,结合频数分布直方图提供的信息,解答下列问题:
(1)八(1)班共有多少名学生?
(2)求在69.5~79.5分的人数,并补全频数分布直方图;
(3)将全班同学的成绩绘制成扇形统计图,若80分及80分以上为优秀,则优秀人数所在扇形圆心角的度数为多少?
22.如图,已知,直线交于点,交于点,是线段上一动点(不与点重合).
(1)若,求的度数;
(2)若,求与的度数之和(用含的代数式表示).
23.字水中学十分重视培养学生的综合素质,组织七年级学生参加研学活动,需租用两种不同型号的客车,每辆座位如下表:若租用型客车5辆和型客车2辆,则需要租金2500元;若租用型客车1辆和型客车5辆,则需要租金2800元.
客车型号
人数/辆 30 45
(1)求租用、两种型号客车,每辆车租金分别是多少元?
(2)现有七年级师生450人,现计划同时租用两种型号客车,一次送完,且恰好每辆车都坐满,有几种租车方案?为节约成本,则租用A型客车和B型客车各多少辆,需要花费多少钱?
24.在数学学习中,通常用两种不同的方法计算同一个图形的面积,可以得到一个恒等式,充分体现了数形结合的思想方法.如图,用图1三种不同大小的正方形与长方形若干个,可以拼成一个如图2所示的正方形.
(1)观察猜想:观察图2,用两种不同的方法表示图2阴影部分的面积则可得,,之间的数量关系为:______;
(2)理解运用:若,,根据(1)中得出的数量关系,求,的值;
(3)拓展提升:若满足,求的值.
25.已知,点、分别在直线、上,点在、之间,连接、,设,(、均小于).
(1)如图1,试说明.
(2)点是下方一点,连接,线段与射线交于点.
①如图2,当点在线段上时,若,求的度数(结果用含的代数式表示);
②如图3,当点在线段延长线上时,若平分平分,,求的度数.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B A D C A B B C C
二、填空题
11.【解】解:由表可知,当n很大时,摸到黑球的频率将会接近,
所以黑球的个数约为个,
故答案为:.
12.【解】解:如图所示,∵,
∴,
∵,
∴,
∴,
故答案为:.
13.【解】解:令,,则关于,的方程组可转化为.
是的解,
.
解,得;解,得.
故答案为: .
14.【解】解:
,
∵与的乘积中不含的一次项,
,解得,.
故答案为:.
15.【解】解:∵120 是平方差分解数,即 对于正整数 .
根据平方差公式,.
设 ,,则 ,且 , 和 同奇偶(因为 , 需为整数)
120 的因子对及同奇偶检查:
经检验,有效数对为 、、、.
最小 为 2(对应 ).
此时,,.
验证:.
最优分解为 ,.
则:
∵ 是三位数,其中 ,,( 隐含为整数且 ,因 为三位数).
∵个位数字与十位数字相同.设十位和个位数字均为 ,则 .由 ,得:
即 被 11 整除.
设 ( 为整数,),则:,为整数,
又∵,余数为 5
所以 .为整数,
的可能 值为:17, 28, 39, 50, 61, 72, 83, 94.
经检验,∶ ,,.
∶ ,,.
∶ ,,.
数字和 .
∵, 为 5 的整数倍.
恒成立.
为整数,故 整除 10,且 (因 ).
10 的因子 ∶ 5, 10.
所以 或 ,即 或 .
若 ,∶
需为 5 的倍数:
()∶ (不满足).
()∶ (满足).
()∶ (不满足).
所以 ,,.
若 ,∶
需为 5 的倍数:
()∶ (不满足).
()∶ (不满足).
()∶ (满足).
所以 ,,.
可能 值:388 和 899.
需为平方差分解数:
∶ 分解为 .
经检验有效数对为:.
,.
验证:,最小 .是平方差分解数.
∶ 分解为 .
因子对:(同奇),(同奇).
最小 (对应 ):
,.
验证:.是平方差分解数.
满足条件的 中最小值为 388(因 ).
最优分解为 ,.
则:
∴
故答案为:,.
16.【解】解:设,,
,
,
若点M在直线上方时,如图,
,
若点M在直线与之间时,如图,
综上所述或,
故答案为:或.
三、解答题
17.【解】(1)解:
①+②,得
将代入①,得,
∴原方程组的解为.
(2)解:
方程组整理为:
,得,
解得,
将代入②,得,
∴原方程组的解为.
18.【解】(1)解:两方程组化简可得,,
∵两方程组同解,
∴,
得:,
解得:,
把代入①式得:,
∴两个方程组的相同解为;
(2)解:把代入方程组可得:
,
式得:,
解得:,
把代入②式得:,
∴.
19.【解】解:.
当时,
原式.
20.【解】(1)解:∵,
∴.
∵,即.
根据(且,、是正整数),则,
∴,
解得.
(2)解:∵,.
∴.
∵,
∴,,,,
∴.
(3)解:∵, ,
∴.
又∵,
∴把代入,得.
21.【解】(1)解:(人),
答:八(1)班共有50名学生;
(2)解:的人数为(人),
补全图形如下:
;
(3)解:
答:优秀人数所在扇形圆心角的度数为.
22.【解】(1)解:过点作,而,
则,
∴
∵ ,
∴ ,
∴.
(2)解:由(1)知,
∵ ,
∴ ,
∴,
∴.
23.【解】(1)解:设租用A、B两种型号客车,每辆车租金分别是、元,
由题意得:,解得:,
答:租用A、B两种型号客车,每辆车租金分别是、元;
(2)解:设租用A型客车辆,租用B型客车辆,
则,
则,
、都是正整数,
当时,,此时租车费用为(元);
当时,,此时租车费用为(元);
当时,,此时租车费用为(元);
当时,,此时租车费用为(元);
则为了节约成本,则租用A型客车辆,租用B型客车辆,需要花费元.
24.【解】(1)解:由图2可得,阴影部分的面积等于两个小正方形的面积之和,即为;
阴影部分的面积也等于大正方形的面积减去两个长方的面积,即,
,
故答案为:;
(2)解:∵,
,
解得:,
,
,
,
.
(3)解:设,
,
由(2)知,,
,
,
即.
25.【解】(1)解:过点作,
∵,
∴,
∴,,
∴;
(2)解:①∵,,,
∴,,
∵,
∴,
∴;
②过点作,
∵,
∴,
∴,,
∵平分,
∴,
∵平分,
∴,,
∵,
∴,
∵,
∴,
∵,
又由(1)知:,
∴,
∴,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
