第八章 8.2.1一元线性回归模型--人教A版高中数学选择性必修第三册教学课件(共22张PPT)
文档属性
| 名称 | 第八章 8.2.1一元线性回归模型--人教A版高中数学选择性必修第三册教学课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 883.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:24:27 | ||
图片预览






文档简介
(共22张PPT)
8.2.1 一元线性回归模型
第八章 成对数据的统计分析
数学
2.经历完整的统计活动过程,体会应用统计的思想和方法解决实际问题.
学习目标
1.能结合具体实例,通过分析变量间的关系建立一元线性回归模型,并能说明模型参数的统计意义,提高数据分析能力.
学习重难点
重点:
一元线性回归模型的概念,随机误差的概念、表示与假设.
难点:
回归模型与函数模型的区别,随机误差产生的原因与影响.
课堂导入
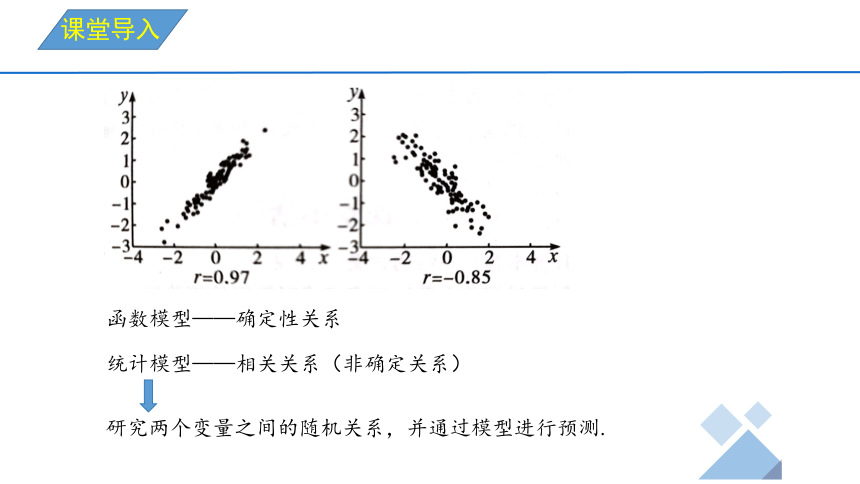
函数模型——确定性关系
统计模型——相关关系(非确定关系)
研究两个变量之间的随机关系,并通过模型进行预测.
课堂导入
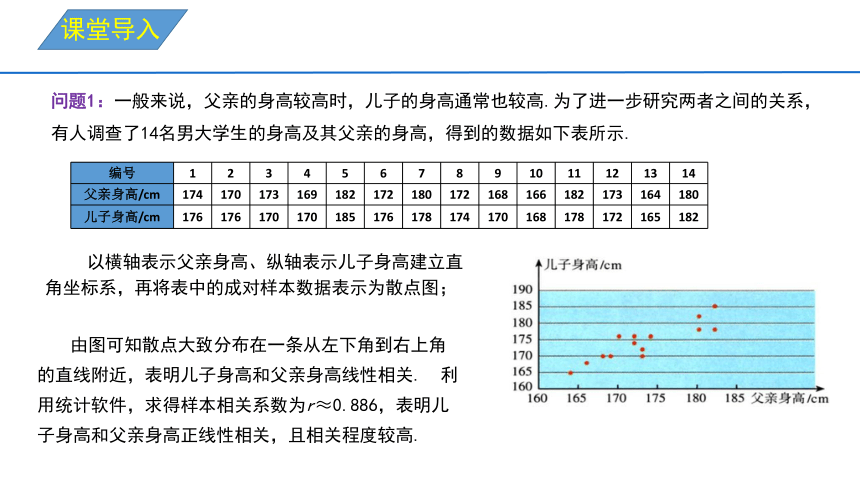
问题1:一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如下表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
以横轴表示父亲身高、纵轴表示儿子身高建立直角坐标系,再将表中的成对样本数据表示为散点图;
由图可知散点大致分布在一条从左下角到右上角的直线附近,表明儿子身高和父亲身高线性相关. 利用统计软件,求得样本相关系数为r≈0.886,表明儿子身高和父亲身高正线性相关,且相关程度较高.
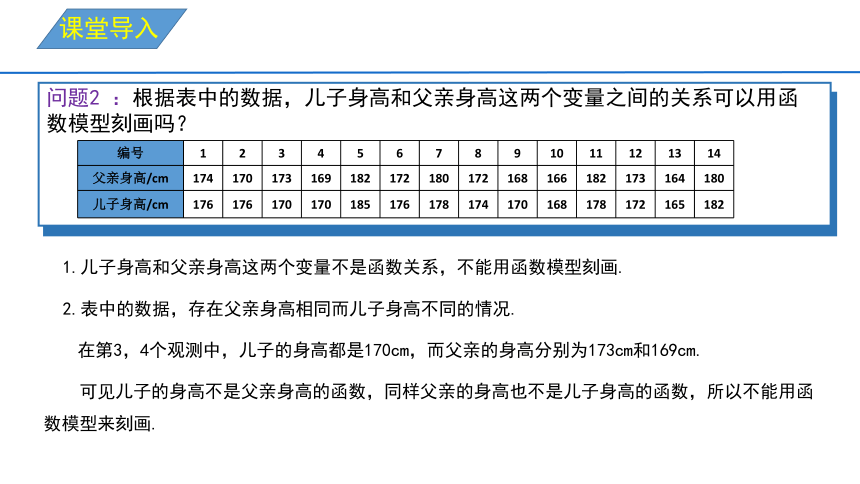
问题2 :根据表中的数据,儿子身高和父亲身高这两个变量之间的关系可以用函数模型刻画吗?
课堂导入
1.儿子身高和父亲身高这两个变量不是函数关系,不能用函数模型刻画.
2.表中的数据,存在父亲身高相同而儿子身高不同的情况.
在第3,4个观测中,儿子的身高都是170cm,而父亲的身高分别为173cm和169cm.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
可见儿子的身高不是父亲身高的函数,同样父亲的身高也不是儿子身高的函数,所以不能用函数模型来刻画.
课堂探究
问题3 :因为存在这些随机的因素,使得儿子的身高呈现出随机性.各种随机因素都是独立的,有些因素又无法量化.考虑到这些随机因素的作用,我们该如何引入适当的变量,借助一次函数关系刻画父亲身高对儿子身高的影响呢?
若用 x 表示父亲身高,Y 表示儿子身高,e 表示随机误差,则
假定随机误差 e 的均值为 0,方差为与父亲身高无关的定值 σ2.
课堂探究
思考:
为什么要假设 E(e)=0,而不假设其为某个不为 0 的常数?
①因为误差是随机的,即取各种正负误差的可能性一样,所以它们均值的理想状态应该为0.
②如果随机误差是一个不为0的常数α,则可以将α合并到截距项a中,否则模型无法确定,即参数没有唯一解.
③如果α不为0,则表示存在系统误差,在实际建模中也不希望模型有系统误差,即模型不存在非随机误差.
课堂探究
问题4:根据以上的分析,你能建立一个数学模型表示儿子身高与父亲身高的关系吗?
我们称(1)式为Y 关于x的一元线性回归模型.
其中,Y称为因变量或响应变量,x称为自变量或解释变量;
a和b为模型的未知参数,a称为截距参数,b称为斜率参数;
e是Y与bx+a之间的随机误差.
模型中的Y也是随机变量,其值虽不能由变量x的值确定,但却能表示为bx+a与e的和,前一部分由x所确定,后一部分是随机的.
如果e=0,那么Y与x之间的关系就可用一元线性函数模型来描述.
课堂探究
思考
结合父亲与儿子身高的实例,说明回归模型(1)的意义?
对于父亲身高x和儿子身高Y的一元线性回归模型(1),可以解释为:父亲身高为xi的所有男大学生的身高组成一个子总体,该子总体的均值为bxi+a,即该子总体的均值与父亲身高是线性函数关系.
思考
对于父亲身高为xi 的某一名男大学生,他的身高yi一定是bxi+a吗?
对于父亲身高为xi的某一名男大学生,他的身高yi并不一定为bxi+a,它仅是该子总体中的一个观测值,这个观测值与均值有一个误差项ei=yi-(bxi+a).
课堂探究
1.在研究儿子身高与父亲身高的关系时,产生随机误差 e 的原因有:
(1) 除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等;
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差;
(3)实际问题中,我们不知道儿子身高和父亲身高的相关关系是什么,利用一元线性回归模型来近似这种关系,这种近似也是产生随机误差e的原因.
问题5:如何理解随机误差e对儿子身高的影响?
课堂探究
问题5:如何理解随机误差e对儿子身高的影响?
假设没有随机误差,则儿子身高Y只受父亲身高x影响,则Y=bx+a
也可以记作
Y=bx+a+e
随机误差e
随机误差 e 的特征
随机误差e是一个随机变量
①可取正或取负
②有些无法测量
③不可事先设定
对于任意一组(xi,Yi),都有一个ei与之对应
课堂探究
函数模型与回归模型之间的差别
函数模型:
回归模型:
一元线性回归模型Y=bx+a+e 增加了随机误差项e,因变量Y的值由自变量x和随机误差项e共同确定,即自变量x只能解释部分Y的变化.
解释变量x (身高)
模型误差e (其它所有变量)
响应变量Y(体重)
举例:①路程与速度的关系②正方体体积与边长的关系可以应用函数模型刻画③体重与身高的关系④冷饮销量与气温的关系可以用回归模型刻画。
典例解析
例:儿童的身高随年龄的增加而增加,我国0~12岁儿童的平均身高如表所示.
课堂探究
年龄/岁 1 2 3 4 5 6 7 8 9 10 11 12
平均身高/cm 76.5 86.5 96.8 104.1 111.3 117.7 124.0 130.0 135.4 140.2 145.3 151.9
解:(1)①用散点图定性分析
②用线性相关系数r进行定量分析
综上,可以用一元线性回归模型进行刻画.
(1)儿童的平均身高Y与年龄t之间能否用一元线性回归模型来刻画?
(2)请说明模型中bx+a和e在本题中的具体含义是什么?
(2)bx+a表示年龄对儿童平均身高的主要影响;
e表示其它因素对儿童平均身高的次要影响.
随堂练习
若某地财政收入x与支出y满足一元线性回归模型 y=bx+a+e (单元:亿元),其中 b=0.7,a=3,|e|≤0.5,如果今年该地区财政收入为10亿元,今年支出预计不会超过多少?
解:因为财政收入x与支出y满足一元线性回归模型 y=bx+a+e,
其中 b=0.7,a=3,所以得到 y=0.7 x+3+e,
当 x=10 时,得 y=0.7×10+3+e=10+e,
而 |e| ≤0.5,即-0.5≤ e ≤0.5,所以 9.5≤ y ≤10.5,
所以今年支出预计不会超过 10.5 亿元.
练一练
名师解惑
一元线性回归模型
1.定义与公式:
2.模型假设:
(1)线性关系假设:Y与X之间存在线性关系.
(2)独立性假设:观测值之间相互独立.
(3)正态性假设:误差项服从均值为0,方差为 的正态分布.
3.常见误区:两个变量不是线性相关关系,却生搬硬套一元线性回归模型 .
评价反馈
解 (1),(2),(3),(4),(5)回归模型 (6),(7)函数模型.
1.判断下列变量间哪些能用函数模型刻画,哪些能用回归模型刻画
(1)某公司的销售收入和广告支出;
(2)某城市写字楼的出租率和每平米月租金;
(3)航空公司的顾客投诉次数和航班正点率;
(4)某地区的人均消费水平和人均国内生产总值(GDP);
(5)学生期末考试成绩和考前用于复习的时间;
(6)一辆汽车在某段路程中的行驶速度和行驶时间;
(7)正方形的面积与周长.
评价反馈
2.(多选)如图,在四个散点图中,适合用一元线性回归模型拟合其中两个变量的是( )
AC
评价反馈
3.工人工资y(单位:元)与劳动生产率x(单位:千元)的线性回归方程为=50+80x,下列判断正确的是( )
A.劳动生产率为1 000元时,工人工资为130元
B.劳动生产率提高1 000元时,工人工资平均提高80元
C.劳动生产率提高1 000元时,工人工资平均提高130元
D.当月工资为250元时,劳动生产率为2 000元
解:因为回归直线的斜率为80,所以x每增加1,y平均增加80,即劳动生产率提高1 000元时,工人工资平均提高80元.
B
回顾建立一元线性回归模型的过程,你能说出建立回归模型的依据,并谈一谈对回归模型的认识吗?
课堂小结
建立一元线性回归模型的步骤
定性分析
定量分析
函数关系或相关关系或没有关系
其中,Y称为因变量或响应变量,x称为自变量或解释变量;a和b为模型的未知参数,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
(3)如果线性相关,建立一元线性回归模型(否则就是其它曲线回归模型)
(2)分析数据
(1)整理数据:散点图
教科书第107页练习第2,3题.
布置作业
谢谢大家
8.2.1 一元线性回归模型
第八章 成对数据的统计分析
数学
2.经历完整的统计活动过程,体会应用统计的思想和方法解决实际问题.
学习目标
1.能结合具体实例,通过分析变量间的关系建立一元线性回归模型,并能说明模型参数的统计意义,提高数据分析能力.
学习重难点
重点:
一元线性回归模型的概念,随机误差的概念、表示与假设.
难点:
回归模型与函数模型的区别,随机误差产生的原因与影响.
课堂导入
函数模型——确定性关系
统计模型——相关关系(非确定关系)
研究两个变量之间的随机关系,并通过模型进行预测.
课堂导入
问题1:一般来说,父亲的身高较高时,儿子的身高通常也较高.为了进一步研究两者之间的关系,有人调查了14名男大学生的身高及其父亲的身高,得到的数据如下表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
以横轴表示父亲身高、纵轴表示儿子身高建立直角坐标系,再将表中的成对样本数据表示为散点图;
由图可知散点大致分布在一条从左下角到右上角的直线附近,表明儿子身高和父亲身高线性相关. 利用统计软件,求得样本相关系数为r≈0.886,表明儿子身高和父亲身高正线性相关,且相关程度较高.
问题2 :根据表中的数据,儿子身高和父亲身高这两个变量之间的关系可以用函数模型刻画吗?
课堂导入
1.儿子身高和父亲身高这两个变量不是函数关系,不能用函数模型刻画.
2.表中的数据,存在父亲身高相同而儿子身高不同的情况.
在第3,4个观测中,儿子的身高都是170cm,而父亲的身高分别为173cm和169cm.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
可见儿子的身高不是父亲身高的函数,同样父亲的身高也不是儿子身高的函数,所以不能用函数模型来刻画.
课堂探究
问题3 :因为存在这些随机的因素,使得儿子的身高呈现出随机性.各种随机因素都是独立的,有些因素又无法量化.考虑到这些随机因素的作用,我们该如何引入适当的变量,借助一次函数关系刻画父亲身高对儿子身高的影响呢?
若用 x 表示父亲身高,Y 表示儿子身高,e 表示随机误差,则
假定随机误差 e 的均值为 0,方差为与父亲身高无关的定值 σ2.
课堂探究
思考:
为什么要假设 E(e)=0,而不假设其为某个不为 0 的常数?
①因为误差是随机的,即取各种正负误差的可能性一样,所以它们均值的理想状态应该为0.
②如果随机误差是一个不为0的常数α,则可以将α合并到截距项a中,否则模型无法确定,即参数没有唯一解.
③如果α不为0,则表示存在系统误差,在实际建模中也不希望模型有系统误差,即模型不存在非随机误差.
课堂探究
问题4:根据以上的分析,你能建立一个数学模型表示儿子身高与父亲身高的关系吗?
我们称(1)式为Y 关于x的一元线性回归模型.
其中,Y称为因变量或响应变量,x称为自变量或解释变量;
a和b为模型的未知参数,a称为截距参数,b称为斜率参数;
e是Y与bx+a之间的随机误差.
模型中的Y也是随机变量,其值虽不能由变量x的值确定,但却能表示为bx+a与e的和,前一部分由x所确定,后一部分是随机的.
如果e=0,那么Y与x之间的关系就可用一元线性函数模型来描述.
课堂探究
思考
结合父亲与儿子身高的实例,说明回归模型(1)的意义?
对于父亲身高x和儿子身高Y的一元线性回归模型(1),可以解释为:父亲身高为xi的所有男大学生的身高组成一个子总体,该子总体的均值为bxi+a,即该子总体的均值与父亲身高是线性函数关系.
思考
对于父亲身高为xi 的某一名男大学生,他的身高yi一定是bxi+a吗?
对于父亲身高为xi的某一名男大学生,他的身高yi并不一定为bxi+a,它仅是该子总体中的一个观测值,这个观测值与均值有一个误差项ei=yi-(bxi+a).
课堂探究
1.在研究儿子身高与父亲身高的关系时,产生随机误差 e 的原因有:
(1) 除父亲身高外,其他可能影响儿子身高的因素,比如母亲身高、生活环境、饮食习惯和锻炼时间等;
(2)在测量儿子身高时,由于测量工具、测量精度所产生的测量误差;
(3)实际问题中,我们不知道儿子身高和父亲身高的相关关系是什么,利用一元线性回归模型来近似这种关系,这种近似也是产生随机误差e的原因.
问题5:如何理解随机误差e对儿子身高的影响?
课堂探究
问题5:如何理解随机误差e对儿子身高的影响?
假设没有随机误差,则儿子身高Y只受父亲身高x影响,则Y=bx+a
也可以记作
Y=bx+a+e
随机误差e
随机误差 e 的特征
随机误差e是一个随机变量
①可取正或取负
②有些无法测量
③不可事先设定
对于任意一组(xi,Yi),都有一个ei与之对应
课堂探究
函数模型与回归模型之间的差别
函数模型:
回归模型:
一元线性回归模型Y=bx+a+e 增加了随机误差项e,因变量Y的值由自变量x和随机误差项e共同确定,即自变量x只能解释部分Y的变化.
解释变量x (身高)
模型误差e (其它所有变量)
响应变量Y(体重)
举例:①路程与速度的关系②正方体体积与边长的关系可以应用函数模型刻画③体重与身高的关系④冷饮销量与气温的关系可以用回归模型刻画。
典例解析
例:儿童的身高随年龄的增加而增加,我国0~12岁儿童的平均身高如表所示.
课堂探究
年龄/岁 1 2 3 4 5 6 7 8 9 10 11 12
平均身高/cm 76.5 86.5 96.8 104.1 111.3 117.7 124.0 130.0 135.4 140.2 145.3 151.9
解:(1)①用散点图定性分析
②用线性相关系数r进行定量分析
综上,可以用一元线性回归模型进行刻画.
(1)儿童的平均身高Y与年龄t之间能否用一元线性回归模型来刻画?
(2)请说明模型中bx+a和e在本题中的具体含义是什么?
(2)bx+a表示年龄对儿童平均身高的主要影响;
e表示其它因素对儿童平均身高的次要影响.
随堂练习
若某地财政收入x与支出y满足一元线性回归模型 y=bx+a+e (单元:亿元),其中 b=0.7,a=3,|e|≤0.5,如果今年该地区财政收入为10亿元,今年支出预计不会超过多少?
解:因为财政收入x与支出y满足一元线性回归模型 y=bx+a+e,
其中 b=0.7,a=3,所以得到 y=0.7 x+3+e,
当 x=10 时,得 y=0.7×10+3+e=10+e,
而 |e| ≤0.5,即-0.5≤ e ≤0.5,所以 9.5≤ y ≤10.5,
所以今年支出预计不会超过 10.5 亿元.
练一练
名师解惑
一元线性回归模型
1.定义与公式:
2.模型假设:
(1)线性关系假设:Y与X之间存在线性关系.
(2)独立性假设:观测值之间相互独立.
(3)正态性假设:误差项服从均值为0,方差为 的正态分布.
3.常见误区:两个变量不是线性相关关系,却生搬硬套一元线性回归模型 .
评价反馈
解 (1),(2),(3),(4),(5)回归模型 (6),(7)函数模型.
1.判断下列变量间哪些能用函数模型刻画,哪些能用回归模型刻画
(1)某公司的销售收入和广告支出;
(2)某城市写字楼的出租率和每平米月租金;
(3)航空公司的顾客投诉次数和航班正点率;
(4)某地区的人均消费水平和人均国内生产总值(GDP);
(5)学生期末考试成绩和考前用于复习的时间;
(6)一辆汽车在某段路程中的行驶速度和行驶时间;
(7)正方形的面积与周长.
评价反馈
2.(多选)如图,在四个散点图中,适合用一元线性回归模型拟合其中两个变量的是( )
AC
评价反馈
3.工人工资y(单位:元)与劳动生产率x(单位:千元)的线性回归方程为=50+80x,下列判断正确的是( )
A.劳动生产率为1 000元时,工人工资为130元
B.劳动生产率提高1 000元时,工人工资平均提高80元
C.劳动生产率提高1 000元时,工人工资平均提高130元
D.当月工资为250元时,劳动生产率为2 000元
解:因为回归直线的斜率为80,所以x每增加1,y平均增加80,即劳动生产率提高1 000元时,工人工资平均提高80元.
B
回顾建立一元线性回归模型的过程,你能说出建立回归模型的依据,并谈一谈对回归模型的认识吗?
课堂小结
建立一元线性回归模型的步骤
定性分析
定量分析
函数关系或相关关系或没有关系
其中,Y称为因变量或响应变量,x称为自变量或解释变量;a和b为模型的未知参数,a称为截距参数,b称为斜率参数;e是Y与bx+a之间的随机误差.
(3)如果线性相关,建立一元线性回归模型(否则就是其它曲线回归模型)
(2)分析数据
(1)整理数据:散点图
教科书第107页练习第2,3题.
布置作业
谢谢大家
