第八章 8.2.2一元线性回归模型参数的最小二乘估计 第1课时--人教A版高中数学必修第三册教学课件(共25张PPT)
文档属性
| 名称 | 第八章 8.2.2一元线性回归模型参数的最小二乘估计 第1课时--人教A版高中数学必修第三册教学课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:24:34 | ||
图片预览


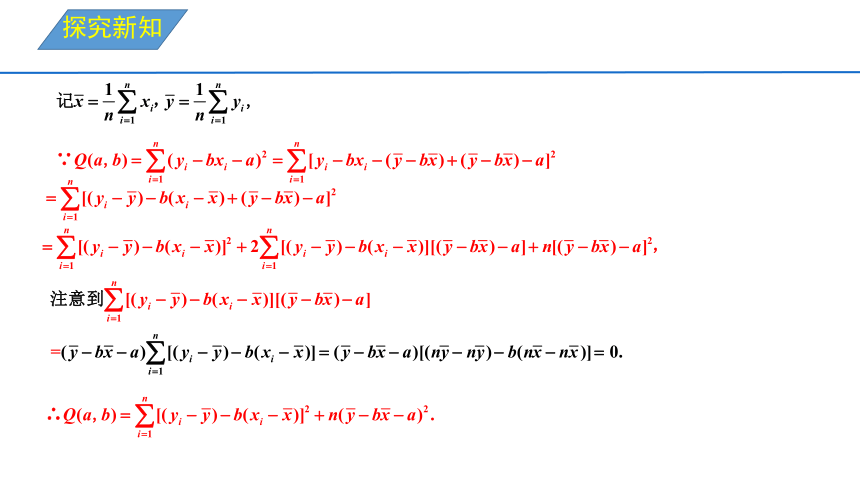


文档简介
(共25张PPT)
8.2.2 一元线性回归模型参数的最小二乘估计
第1课时
第八章 成对数据的统计分析
数学
学习目标
①通过用数学方法刻画散点与直线接近的程度,体会一元线性回归模型参数的最小二乘估计原理.
②根据最小二乘法参数估计,会计算经验回归方程,并进行预测.
③通过对残差和残差图的分析,能用残差判断一元线性回归模型的有效性.
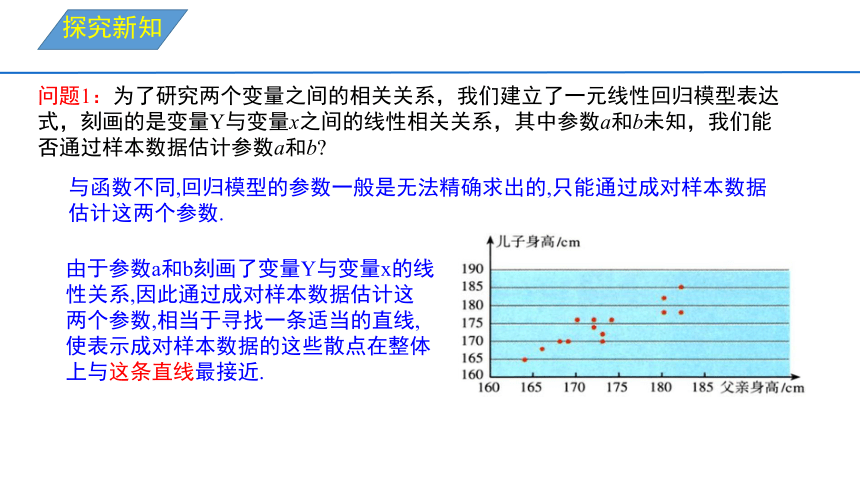
问题1:为了研究两个变量之间的相关关系,我们建立了一元线性回归模型表达式,刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,我们能否通过样本数据估计参数a和b
与函数不同,回归模型的参数一般是无法精确求出的,只能通过成对样本数据估计这两个参数.
由于参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
探究新知
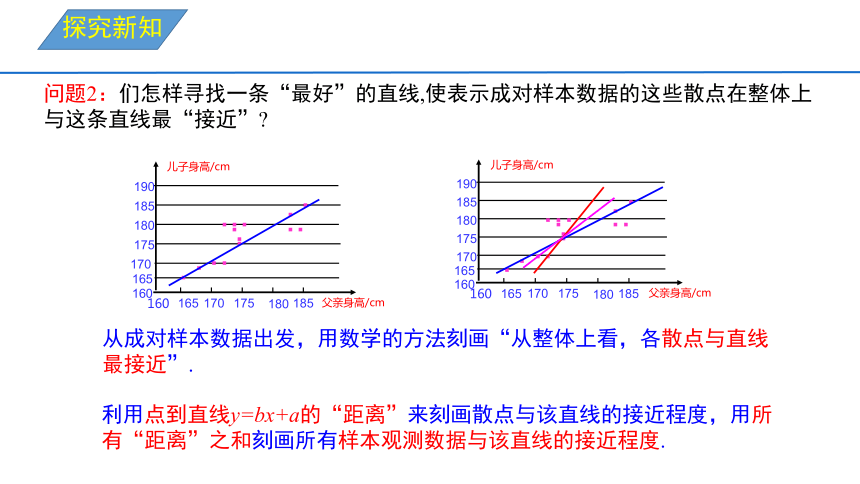
问题2:们怎样寻找一条“最好”的直线,使表示成对样本数据的这些散点在整体上与这条直线最“接近”
从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.
利用点到直线y=bx+a的“距离”来刻画散点与该直线的接近程度,用所有“距离”之和刻画所有样本观测数据与该直线的接近程度.
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
探究新知
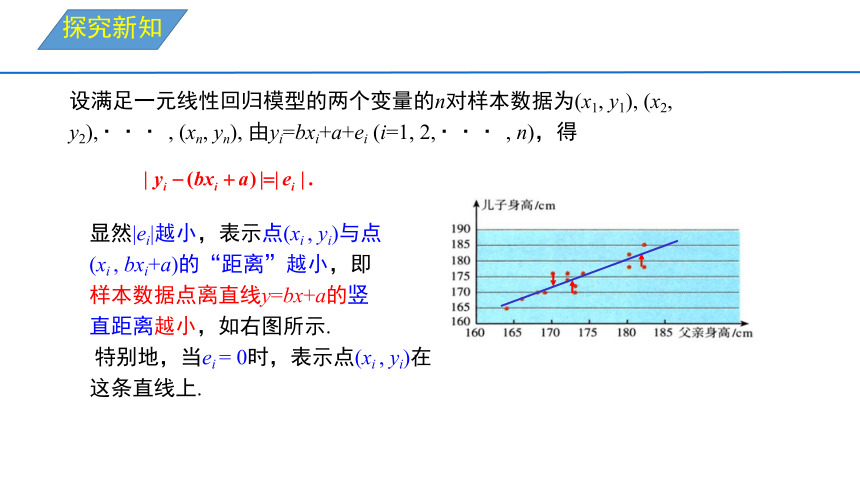
设满足一元线性回归模型的两个变量的n对样本数据为(x1, y1), (x2,
y2), , (xn, yn), 由yi=bxi+a+ei (i=1, 2, , n),得
显然|ei|越小,表示点(xi , yi)与点
(xi , bxi+a)的“距离”越小,即
样本数据点离直线y=bx+a的竖
直距离越小,如右图所示.
特别地,当ei = 0时,表示点(xi , yi)在
这条直线上.
探究新知
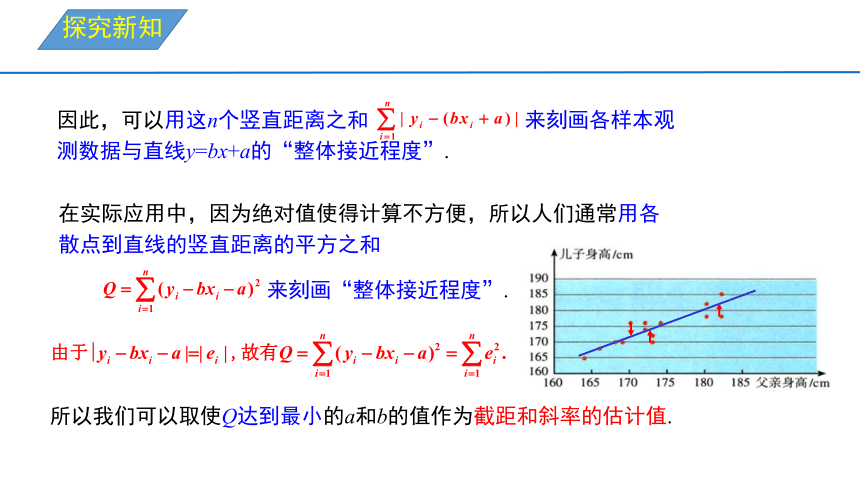
因此,可以用这n个竖直距离之和 来刻画各样本观
测数据与直线y=bx+a的“整体接近程度”.
在实际应用中,因为绝对值使得计算不方便,所以人们通常用各
散点到直线的竖直距离的平方之和
来刻画“整体接近程度”.
所以我们可以取使Q达到最小的a和b的值作为截距和斜率的估计值.
探究新知
探究新知
要使Q取到最小值,则
∴要使Q取得最小值,当且仅当b的取值为
综上,当a, b的取值为
时,Q达到最小.
探究新知
经验回归方程与最小二乘估计:
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线. 这种求经验回归方程的方法叫做最小二乘法,利用公式
(2)求得的 叫做b, a的最小二乘估计.
易得(1)经验回归直线必过点 ;
(2) 与相关系数r符号相同.
知识小结
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
对于上表中的数据,利用公式可以计算出
得到儿子身高Y关于父亲身高x的经验回归方程为
相应的经验回归直线如图所示.
探究新知
探究新知
问题3:(1)当x=176时, ,如果一位父亲的身高为176 cm,他儿子长大成人后的身高一定是177 cm吗 为什么
儿子的身高不一定会是177 cm,这是因为还有其他影响儿子身高的因素,回归模型中的随机误差清楚地表达了这种影响,父亲身高不能完全决定儿子身高.不过,我们可以作出推测,当父亲身高为176 cm时,儿子身高一般在177 cm左右.
探究新知
(2)根据经验回归方程中斜率的具体含义,高个子的父亲一定生高个子的儿子吗 同样,矮个子的父亲一定生矮个子的儿子吗
并不一定.根据经验回归方程 中斜率0.839可以解释为父亲身高每增加1 cm,其儿子的身高平均增加0.839 cm.由模型可以发现,高个子父亲有生高个子儿子的趋势,但一群高个子父亲的儿子们的平均身高要低于父亲们的身高,例如x=185(cm),则 (cm);矮个子父亲有生矮个子儿子的趋势,但一群矮个子父亲的儿子们的平均身高要高于父亲们的平均身高,例如x=170(cm),则 (cm).
残差分析:
探究新知
(1)残差的定义
一元线性回归模型Y=bx+a+e,对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的y 称为预测值,观测值减去预测值所得的差称为残差.
(2)残差分析
我们可以通过残差e 1,e 2,…,e n来判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.
问题4:儿子身高与父亲身高的关系,运用残差分析所得的一元线性回归模型的有效性吗?
探究新知
编号 父亲身高/cm 儿子身高观测值/cm 儿子身高预测值/cm 残差/cm
1 174 176 174.943 1.057
2 170 176 171.587 4.413
3 173 170 174.104 -4.104
4 169 170 170.748 -0.748
5 182 185 181.655 3.345
6 172 176 173.265 2.735
7 180 178 179.977 -1.977
8 172 174 173.265 0.735
9 168 170 169.909 0.091
10 166 168 168.231 -0.231
11 182 178 181.655 -3.655
12 173 172 174.104 -2.104
13 164 165 166.553 -1.533
14 180 182 179.977 2.023
残差图:作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据或体重估计值等,这样作出的图形称为残差图.
从上面的残差图可以看出,残差有正有负,残差点比较均匀地分布在横轴的两边,可以判断样本数据基本满足一元线性回归模型对于随机误差的假设.所以,通过观察残差图可以直观判断模型是否满足一元线性回归模型的假设,从而判断回归模型拟合的有效性.
探究新知
问题5:观察以下四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
探究新知
图(1)显示残差与观测时间有线性关系,应将时间变量纳入模型;
图(2)显示残差与观测时间有非线性关系,应在模型中加入时间的非线性函数部分;
只有图(4)满足一元线性回归模型对随机误差的假设
图(3)说明残差的方差不是一个常数,随观测时间变大而变大;
图(4)的残差比较均匀地集中在以横轴为对称轴的水平带状区域内.
1.残差等于观测值减预测值;
2.残差的平方和越小越好;
3.原始数据中的可疑数据往往是残差绝对值过大的数据;
4. 对数据刻画效果比较好的残差图特征:残差点比较均匀地集中在水平带状区域内.
知识小结
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
例1:某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1) 画出销售额和利润额的散点图;
(2) 计算利润额y对销售额x的经验回归方程.
解:(1) 散点图如下:
学以致用
∴所求经验回归方程为
(2)公式1:
学以致用
∴所求经验回归方程为
公式2:
学以致用
1.关于残差图的描述错误的是( )
A.残差图的横坐标可以是样本编号
B.残差图的横坐标可以是解释变量
C.残差点分布的带状区域的宽度越窄样本相关指数越小
D.残差点分布的带状区域的宽度越窄残差平方和越小
C
评价反馈
2.已知变量x,y之间具有线性相关关系,其散点图如图所示,
则其经验回归方程可能为( )
B
评价反馈
10
评价反馈
3.某种产品的广告支出费用x(单位:万元)与销售额y(单位:万元)的数据如下表所示.
x/万元 2 4 5 6 8
y/万元 30 40 60 50 70
已知y关于x的经验回归方程为=6.5x+17.5,则当广告支出费用为5万元时,残差为 万元.
解析 当x=5时,=6.5×5+17.5=50,表格中对应y=60,于是残差为60-50=10.
1.一元线性回归模型y=bx+a+e含有随机误差e,其中x为解释变量,y响应变量.
2.残差平方和:Q=,残差:-是随机误差的估计值.
3.最小二乘法
课堂小结
将 称为Y关于x的经验回归方程.
谢谢大家
8.2.2 一元线性回归模型参数的最小二乘估计
第1课时
第八章 成对数据的统计分析
数学
学习目标
①通过用数学方法刻画散点与直线接近的程度,体会一元线性回归模型参数的最小二乘估计原理.
②根据最小二乘法参数估计,会计算经验回归方程,并进行预测.
③通过对残差和残差图的分析,能用残差判断一元线性回归模型的有效性.
问题1:为了研究两个变量之间的相关关系,我们建立了一元线性回归模型表达式,刻画的是变量Y与变量x之间的线性相关关系,其中参数a和b未知,我们能否通过样本数据估计参数a和b
与函数不同,回归模型的参数一般是无法精确求出的,只能通过成对样本数据估计这两个参数.
由于参数a和b刻画了变量Y与变量x的线性关系,因此通过成对样本数据估计这两个参数,相当于寻找一条适当的直线,使表示成对样本数据的这些散点在整体上与这条直线最接近.
探究新知
问题2:们怎样寻找一条“最好”的直线,使表示成对样本数据的这些散点在整体上与这条直线最“接近”
从成对样本数据出发,用数学的方法刻画“从整体上看,各散点与直线最接近”.
利用点到直线y=bx+a的“距离”来刻画散点与该直线的接近程度,用所有“距离”之和刻画所有样本观测数据与该直线的接近程度.
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
父亲身高/cm
180
175
170
165
160
160
165
170
175
180
185
190
·
·
·
·
·
·
·
儿子身高/cm
·
·
·
·
·
·
·
185
探究新知
设满足一元线性回归模型的两个变量的n对样本数据为(x1, y1), (x2,
y2), , (xn, yn), 由yi=bxi+a+ei (i=1, 2, , n),得
显然|ei|越小,表示点(xi , yi)与点
(xi , bxi+a)的“距离”越小,即
样本数据点离直线y=bx+a的竖
直距离越小,如右图所示.
特别地,当ei = 0时,表示点(xi , yi)在
这条直线上.
探究新知
因此,可以用这n个竖直距离之和 来刻画各样本观
测数据与直线y=bx+a的“整体接近程度”.
在实际应用中,因为绝对值使得计算不方便,所以人们通常用各
散点到直线的竖直距离的平方之和
来刻画“整体接近程度”.
所以我们可以取使Q达到最小的a和b的值作为截距和斜率的估计值.
探究新知
探究新知
要使Q取到最小值,则
∴要使Q取得最小值,当且仅当b的取值为
综上,当a, b的取值为
时,Q达到最小.
探究新知
经验回归方程与最小二乘估计:
我们将 称为Y关于x的经验回归方程,也称经验回归函数或经验回归公式,其图形称为经验回归直线. 这种求经验回归方程的方法叫做最小二乘法,利用公式
(2)求得的 叫做b, a的最小二乘估计.
易得(1)经验回归直线必过点 ;
(2) 与相关系数r符号相同.
知识小结
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
父亲身高/cm 174 170 173 169 182 172 180 172 168 166 182 173 164 180
儿子身高/cm 176 176 170 170 185 176 178 174 170 168 178 172 165 182
对于上表中的数据,利用公式可以计算出
得到儿子身高Y关于父亲身高x的经验回归方程为
相应的经验回归直线如图所示.
探究新知
探究新知
问题3:(1)当x=176时, ,如果一位父亲的身高为176 cm,他儿子长大成人后的身高一定是177 cm吗 为什么
儿子的身高不一定会是177 cm,这是因为还有其他影响儿子身高的因素,回归模型中的随机误差清楚地表达了这种影响,父亲身高不能完全决定儿子身高.不过,我们可以作出推测,当父亲身高为176 cm时,儿子身高一般在177 cm左右.
探究新知
(2)根据经验回归方程中斜率的具体含义,高个子的父亲一定生高个子的儿子吗 同样,矮个子的父亲一定生矮个子的儿子吗
并不一定.根据经验回归方程 中斜率0.839可以解释为父亲身高每增加1 cm,其儿子的身高平均增加0.839 cm.由模型可以发现,高个子父亲有生高个子儿子的趋势,但一群高个子父亲的儿子们的平均身高要低于父亲们的身高,例如x=185(cm),则 (cm);矮个子父亲有生矮个子儿子的趋势,但一群矮个子父亲的儿子们的平均身高要高于父亲们的平均身高,例如x=170(cm),则 (cm).
残差分析:
探究新知
(1)残差的定义
一元线性回归模型Y=bx+a+e,对于响应变量Y,通过观测得到的数据称为观测值,通过经验回归方程得到的y 称为预测值,观测值减去预测值所得的差称为残差.
(2)残差分析
我们可以通过残差e 1,e 2,…,e n来判断模型刻画数据的效果,以及判断原始数据中是否存在可疑数据等,这方面工作称为残差分析.
问题4:儿子身高与父亲身高的关系,运用残差分析所得的一元线性回归模型的有效性吗?
探究新知
编号 父亲身高/cm 儿子身高观测值/cm 儿子身高预测值/cm 残差/cm
1 174 176 174.943 1.057
2 170 176 171.587 4.413
3 173 170 174.104 -4.104
4 169 170 170.748 -0.748
5 182 185 181.655 3.345
6 172 176 173.265 2.735
7 180 178 179.977 -1.977
8 172 174 173.265 0.735
9 168 170 169.909 0.091
10 166 168 168.231 -0.231
11 182 178 181.655 -3.655
12 173 172 174.104 -2.104
13 164 165 166.553 -1.533
14 180 182 179.977 2.023
残差图:作图时纵坐标为残差,横坐标可以选为样本编号,或身高数据或体重估计值等,这样作出的图形称为残差图.
从上面的残差图可以看出,残差有正有负,残差点比较均匀地分布在横轴的两边,可以判断样本数据基本满足一元线性回归模型对于随机误差的假设.所以,通过观察残差图可以直观判断模型是否满足一元线性回归模型的假设,从而判断回归模型拟合的有效性.
探究新知
问题5:观察以下四幅残差图,你认为哪一个残差满足一元线性回归模型中对随机误差的假定?
探究新知
图(1)显示残差与观测时间有线性关系,应将时间变量纳入模型;
图(2)显示残差与观测时间有非线性关系,应在模型中加入时间的非线性函数部分;
只有图(4)满足一元线性回归模型对随机误差的假设
图(3)说明残差的方差不是一个常数,随观测时间变大而变大;
图(4)的残差比较均匀地集中在以横轴为对称轴的水平带状区域内.
1.残差等于观测值减预测值;
2.残差的平方和越小越好;
3.原始数据中的可疑数据往往是残差绝对值过大的数据;
4. 对数据刻画效果比较好的残差图特征:残差点比较均匀地集中在水平带状区域内.
知识小结
商店名称 A B C D E
销售额x/千万元 3 5 6 7 9
利润额y/百万元 2 3 3 4 5
例1:某连锁经营公司所属5个零售店某月的销售额和利润额资料如下表:
(1) 画出销售额和利润额的散点图;
(2) 计算利润额y对销售额x的经验回归方程.
解:(1) 散点图如下:
学以致用
∴所求经验回归方程为
(2)公式1:
学以致用
∴所求经验回归方程为
公式2:
学以致用
1.关于残差图的描述错误的是( )
A.残差图的横坐标可以是样本编号
B.残差图的横坐标可以是解释变量
C.残差点分布的带状区域的宽度越窄样本相关指数越小
D.残差点分布的带状区域的宽度越窄残差平方和越小
C
评价反馈
2.已知变量x,y之间具有线性相关关系,其散点图如图所示,
则其经验回归方程可能为( )
B
评价反馈
10
评价反馈
3.某种产品的广告支出费用x(单位:万元)与销售额y(单位:万元)的数据如下表所示.
x/万元 2 4 5 6 8
y/万元 30 40 60 50 70
已知y关于x的经验回归方程为=6.5x+17.5,则当广告支出费用为5万元时,残差为 万元.
解析 当x=5时,=6.5×5+17.5=50,表格中对应y=60,于是残差为60-50=10.
1.一元线性回归模型y=bx+a+e含有随机误差e,其中x为解释变量,y响应变量.
2.残差平方和:Q=,残差:-是随机误差的估计值.
3.最小二乘法
课堂小结
将 称为Y关于x的经验回归方程.
谢谢大家
