第八章 8.2.2一元线性回归模型参数的最小二乘估计 第2课时--人教A版高中数学选择性必修第三册教学课件(共30张PPT)
文档属性
| 名称 | 第八章 8.2.2一元线性回归模型参数的最小二乘估计 第2课时--人教A版高中数学选择性必修第三册教学课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:25:05 | ||
图片预览






文档简介
(共30张PPT)
8.2.2 一元线性回归模型参数的最小二乘估计
第2课时
第八章 成对数据的统计分析
数学
学习目标
1.能通过实例说明一元线性回归模型修改的依据和方法.
2.能将某些非线性回归问题转化为线性回归问题并加以解决.
3.能说明R2的意义和作用.
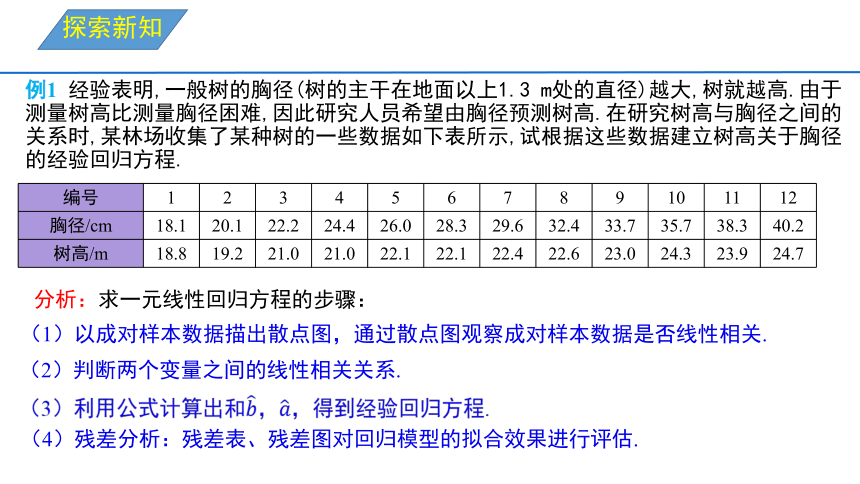
例1 经验表明,一般树的胸径(树的主干在地面以上1.3 m处的直径)越大,树就越高.由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据如下表所示,试根据这些数据建立树高关于胸径的经验回归方程.
编号 1 2 3 4 5 6 7 8 9 10 11 12
胸径/cm 18.1 20.1 22.2 24.4 26.0 28.3 29.6 32.4 33.7 35.7 38.3 40.2
树高/m 18.8 19.2 21.0 21.0 22.1 22.1 22.4 22.6 23.0 24.3 23.9 24.7
分析:求一元线性回归方程的步骤:
(1)以成对样本数据描出散点图,通过散点图观察成对样本数据是否线性相关.
(2)判断两个变量之间的线性相关关系.
(4)残差分析:残差表、残差图对回归模型的拟合效果进行评估.
探索新知
(3)利用公式计算出和,,得到经验回归方程.
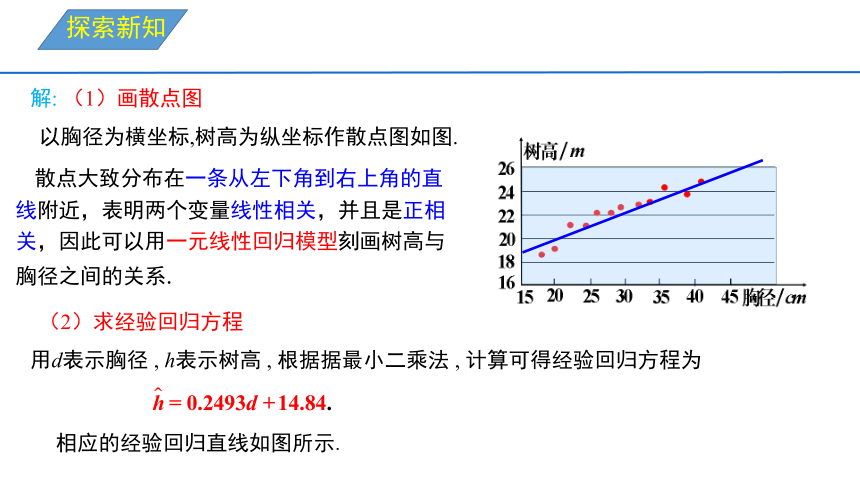
以胸径为横坐标,树高为纵坐标作散点图如图.
散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用一元线性回归模型刻画树高与胸径之间的关系.
用d表示胸径 , h表示树高 , 根据据最小二乘法 , 计算可得经验回归方程为
相应的经验回归直线如图所示.
解: (1)画散点图
(2)求经验回归方程
探索新知
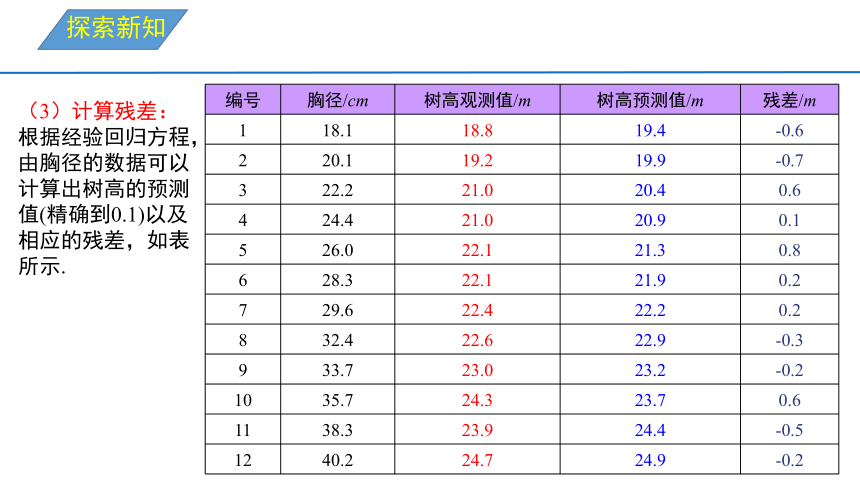
编号 胸径/cm 树高观测值/m 树高预测值/m 残差/m
1 18.1 18.8 19.4 -0.6
2 20.1 19.2 19.9 -0.7
3 22.2 21.0 20.4 0.6
4 24.4 21.0 20.9 0.1
5 26.0 22.1 21.3 0.8
6 28.3 22.1 21.9 0.2
7 29.6 22.4 22.2 0.2
8 32.4 22.6 22.9 -0.3
9 33.7 23.0 23.2 -0.2
10 35.7 24.3 23.7 0.6
11 38.3 23.9 24.4 -0.5
12 40.2 24.7 24.9 -0.2
(3)计算残差:根据经验回归方程,由胸径的数据可以计算出树高的预测值(精确到0.1)以及相应的残差,如表所示.
探索新知
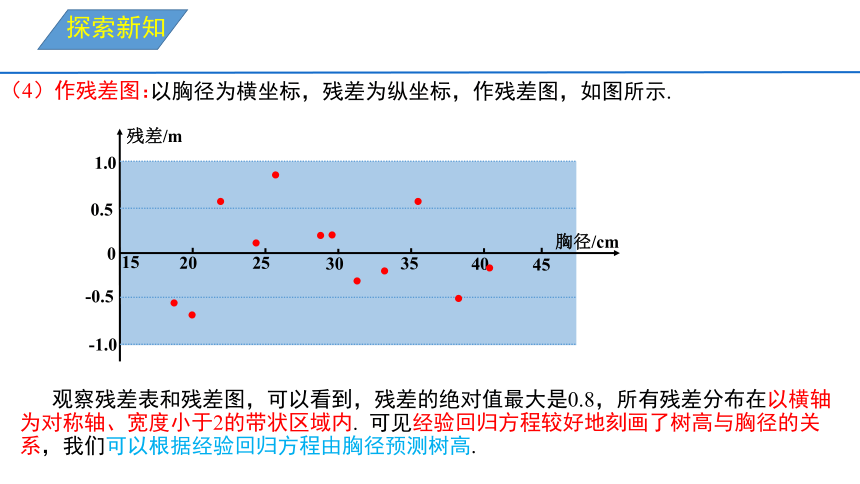
以胸径为横坐标,残差为纵坐标,作残差图,如图所示.
(4)作残差图:
观察残差表和残差图,可以看到,残差的绝对值最大是0.8,所有残差分布在以横轴为对称轴、宽度小于2的带状区域内. 可见经验回归方程较好地刻画了树高与胸径的关系,我们可以根据经验回归方程由胸径预测树高.
0
0.5
1.0
-0.5
-1.0
15
20
25
30
35
40
残差/m
胸径/cm
45
探索新知
建立树的胸径和树高的关系是有实际意义的.实际上,在采伐设计、资源评估、森林规划调查等林业工作中常需测算森林蓄积量.可以从森林中抽取部分树木,通过树的胸径与树高估计抽到的每棵树的体积,进而推断整片森林的蓄积量.
由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.因此,建模时将胸径作为解释变量,树高作为响应变量,即树高作为响应变量是解决实际问题的需要.
回归分析的实际意义
探索新知
探索新知
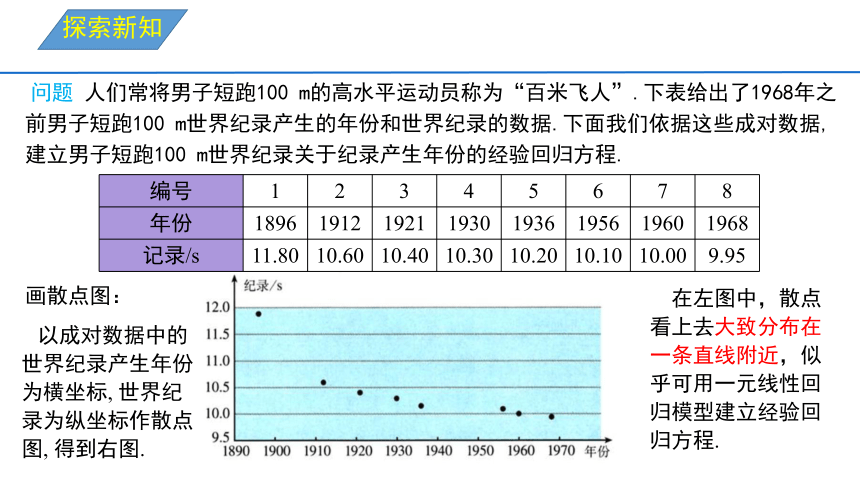
问题 人们常将男子短跑100 m的高水平运动员称为“百米飞人”.下表给出了1968年之前男子短跑100 m世界纪录产生的年份和世界纪录的数据.下面我们依据这些成对数据,建立男子短跑100 m世界纪录关于纪录产生年份的经验回归方程.
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
画散点图:
以成对数据中的世界纪录产生年份为横坐标, 世界纪录为纵坐标作散点图, 得到右图.
在左图中,散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程.
由散点图可知,散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程.
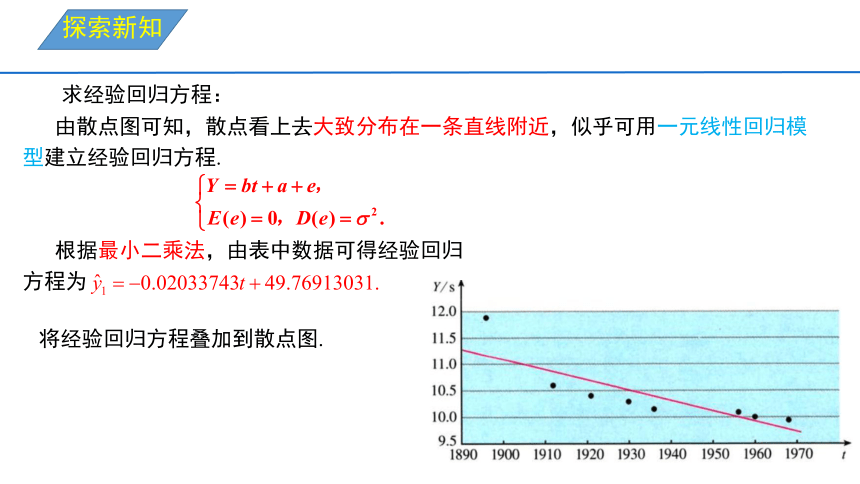
根据最小二乘法,由表中数据可得经验回归
方程为
求经验回归方程:
将经验回归方程叠加到散点图.
探索新知
思考1:仔细观察图中散点与直线的位置关系,你能看出其中存在的问题吗?
由图形可知,第一个世界纪录所对应的散点远离经验回归直线,并且前后两时间段中的散点都在经验回归直线的上方,中间时间段的散点都在经验回归直线的下方.
这说明散点并不是随机分布在经验回归直线的周围,而是围绕着经验回归直线有一定的变化规律,即成对样本数据呈现出明显的非线性相关的特征.
探索新知
思考2:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
散点更趋向于落在中间下凸且递减的某条曲线附近.
已学的函数_________________的图象具有类似的形状特征.
y=﹣ln x
,y=﹣lg x
注意到短跑的第1个世界纪录产生于1896年,因此可以认为散点是集中在曲线y=c1+c2ln(t 189 5)的周围,其中c1和c2为未知参数,且c2<0.
探索新知
思考3:如何利用成对数据估计参数c1和c2?
作出(xi,yi)的散点图,
可见x与y呈现出很强的负线性相关特征.
精确到0.01
探索新知
思考3:如何利用成对数据估计参数c1和c2?
该经验回归方程对于表中的成对数据xi,yi具有非常好的拟合精度.
x和Y之间的线性相关程度比t和Y的线性相关程度强得多.
探索新知
由图可看出,散点图中各散点都非常靠近②的图象,非线性经验回归方程②对于原始数据的拟合效果远远好于线性经验回归方程①
探索新知
思考4:你能否通过残差分析来比较这两个经验回归方程对数据刻画的好坏?
方程②各项残差的绝对值远远小于方程①,即方程②的拟合效果要远远好于①.
探索新知
一般情况下,直接一一比较两个模型的各项残差绝对值比较困难,因为对于某些散点,模型①的残差的绝对值比模型②的小,而另一些散点的情况则相反.
方案二:通过比较残差的平方和来比较两个模型的效果.
在残差平方和最小的标准下,非线性回归模型的拟合效果要优于一元线性回归模型的拟合效果.
方案一:通过比较残差的绝对值之和来比较两个模型的效果.
探索新知
方案三:通过比较决定系数R2来比较两个模型的效果.
残差平方和
总偏差平方和
(与回归方程无关)
(与回归方程有关)
R2越大,残差平方和越小,模型拟合效果越好.
经验回归方程②的刻画效果比经验回归方程①的好很多.
①R2越大,R2越接近1,残差平方和越小,模型拟合效果越好.
②样本相关系数r刻画线性相关关系的正负和强弱;
决定系数R2刻画模型拟合效果的好坏.
知识归纳
例:近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图.
学以致用
(1)根据散点图判断在推广期内,y=a+bx与y=c·dx(c,d为大于0的常数)哪一个适宜作为每天使用扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
【解】根据散点图判断,y=c·dx适宜作为每天使用扫码支付的人次y关于活动推出天数x的回归方程类型.
学以致用
(2)根据(1)的判断结果求y关于x的经验回归方程,并预测活动推出第8天使用扫码支付的人次.参考数据:其中v=lg y,
学以致用
解决非线性回归问题的方法及步骤
知识归纳
评价反馈
评价反馈
评价反馈
评价反馈
评价反馈
(3)当x=40时,y=≈1 131.
在使用经验回归方程进行预测时,需要注意下列问题:
(1) 经验回归方程只适用于所研究的样本的总体. 例如,根据我国父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述美国父亲身高与儿子身高之间的关系.同样,根据生长在南方多雨地区的树高与胸径的数据建立的经验回归方程,不能用来描述北方干旱地区的树高与胸径之间的关系.
(2) 经验回归方程一般都有时效性. 例如,根据20世纪80年代的父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述现在的父亲身高与儿子身高之间的关系.
(3) 解释变量的取值不能离样本数据的范围太远. 一般解释变量的取值在样本数据范围内,经验回归方程的预报效果会比较好,超出这个范围越远,预报的效果越差.
(4) 不能期望经验回归方程得到的预报值就是响应变量的精确值. 事实上,它是响应变量的可能取值的平均值.
课堂小结
课堂小结
1.解决非线性经验回归问题的方法及步骤
2.决定系数R2
显然0≤R2≤1,R2越接近1,则模型拟合的效果越好.
谢谢大家
8.2.2 一元线性回归模型参数的最小二乘估计
第2课时
第八章 成对数据的统计分析
数学
学习目标
1.能通过实例说明一元线性回归模型修改的依据和方法.
2.能将某些非线性回归问题转化为线性回归问题并加以解决.
3.能说明R2的意义和作用.
例1 经验表明,一般树的胸径(树的主干在地面以上1.3 m处的直径)越大,树就越高.由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.在研究树高与胸径之间的关系时,某林场收集了某种树的一些数据如下表所示,试根据这些数据建立树高关于胸径的经验回归方程.
编号 1 2 3 4 5 6 7 8 9 10 11 12
胸径/cm 18.1 20.1 22.2 24.4 26.0 28.3 29.6 32.4 33.7 35.7 38.3 40.2
树高/m 18.8 19.2 21.0 21.0 22.1 22.1 22.4 22.6 23.0 24.3 23.9 24.7
分析:求一元线性回归方程的步骤:
(1)以成对样本数据描出散点图,通过散点图观察成对样本数据是否线性相关.
(2)判断两个变量之间的线性相关关系.
(4)残差分析:残差表、残差图对回归模型的拟合效果进行评估.
探索新知
(3)利用公式计算出和,,得到经验回归方程.
以胸径为横坐标,树高为纵坐标作散点图如图.
散点大致分布在一条从左下角到右上角的直线附近,表明两个变量线性相关,并且是正相关,因此可以用一元线性回归模型刻画树高与胸径之间的关系.
用d表示胸径 , h表示树高 , 根据据最小二乘法 , 计算可得经验回归方程为
相应的经验回归直线如图所示.
解: (1)画散点图
(2)求经验回归方程
探索新知
编号 胸径/cm 树高观测值/m 树高预测值/m 残差/m
1 18.1 18.8 19.4 -0.6
2 20.1 19.2 19.9 -0.7
3 22.2 21.0 20.4 0.6
4 24.4 21.0 20.9 0.1
5 26.0 22.1 21.3 0.8
6 28.3 22.1 21.9 0.2
7 29.6 22.4 22.2 0.2
8 32.4 22.6 22.9 -0.3
9 33.7 23.0 23.2 -0.2
10 35.7 24.3 23.7 0.6
11 38.3 23.9 24.4 -0.5
12 40.2 24.7 24.9 -0.2
(3)计算残差:根据经验回归方程,由胸径的数据可以计算出树高的预测值(精确到0.1)以及相应的残差,如表所示.
探索新知
以胸径为横坐标,残差为纵坐标,作残差图,如图所示.
(4)作残差图:
观察残差表和残差图,可以看到,残差的绝对值最大是0.8,所有残差分布在以横轴为对称轴、宽度小于2的带状区域内. 可见经验回归方程较好地刻画了树高与胸径的关系,我们可以根据经验回归方程由胸径预测树高.
0
0.5
1.0
-0.5
-1.0
15
20
25
30
35
40
残差/m
胸径/cm
45
探索新知
建立树的胸径和树高的关系是有实际意义的.实际上,在采伐设计、资源评估、森林规划调查等林业工作中常需测算森林蓄积量.可以从森林中抽取部分树木,通过树的胸径与树高估计抽到的每棵树的体积,进而推断整片森林的蓄积量.
由于测量树高比测量胸径困难,因此研究人员希望由胸径预测树高.因此,建模时将胸径作为解释变量,树高作为响应变量,即树高作为响应变量是解决实际问题的需要.
回归分析的实际意义
探索新知
探索新知
问题 人们常将男子短跑100 m的高水平运动员称为“百米飞人”.下表给出了1968年之前男子短跑100 m世界纪录产生的年份和世界纪录的数据.下面我们依据这些成对数据,建立男子短跑100 m世界纪录关于纪录产生年份的经验回归方程.
编号 1 2 3 4 5 6 7 8
年份 1896 1912 1921 1930 1936 1956 1960 1968
记录/s 11.80 10.60 10.40 10.30 10.20 10.10 10.00 9.95
画散点图:
以成对数据中的世界纪录产生年份为横坐标, 世界纪录为纵坐标作散点图, 得到右图.
在左图中,散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程.
由散点图可知,散点看上去大致分布在一条直线附近,似乎可用一元线性回归模型建立经验回归方程.
根据最小二乘法,由表中数据可得经验回归
方程为
求经验回归方程:
将经验回归方程叠加到散点图.
探索新知
思考1:仔细观察图中散点与直线的位置关系,你能看出其中存在的问题吗?
由图形可知,第一个世界纪录所对应的散点远离经验回归直线,并且前后两时间段中的散点都在经验回归直线的上方,中间时间段的散点都在经验回归直线的下方.
这说明散点并不是随机分布在经验回归直线的周围,而是围绕着经验回归直线有一定的变化规律,即成对样本数据呈现出明显的非线性相关的特征.
探索新知
思考2:你能对模型进行修改,以使其更好地反映散点的分布特征吗?
散点更趋向于落在中间下凸且递减的某条曲线附近.
已学的函数_________________的图象具有类似的形状特征.
y=﹣ln x
,y=﹣lg x
注意到短跑的第1个世界纪录产生于1896年,因此可以认为散点是集中在曲线y=c1+c2ln(t 189 5)的周围,其中c1和c2为未知参数,且c2<0.
探索新知
思考3:如何利用成对数据估计参数c1和c2?
作出(xi,yi)的散点图,
可见x与y呈现出很强的负线性相关特征.
精确到0.01
探索新知
思考3:如何利用成对数据估计参数c1和c2?
该经验回归方程对于表中的成对数据xi,yi具有非常好的拟合精度.
x和Y之间的线性相关程度比t和Y的线性相关程度强得多.
探索新知
由图可看出,散点图中各散点都非常靠近②的图象,非线性经验回归方程②对于原始数据的拟合效果远远好于线性经验回归方程①
探索新知
思考4:你能否通过残差分析来比较这两个经验回归方程对数据刻画的好坏?
方程②各项残差的绝对值远远小于方程①,即方程②的拟合效果要远远好于①.
探索新知
一般情况下,直接一一比较两个模型的各项残差绝对值比较困难,因为对于某些散点,模型①的残差的绝对值比模型②的小,而另一些散点的情况则相反.
方案二:通过比较残差的平方和来比较两个模型的效果.
在残差平方和最小的标准下,非线性回归模型的拟合效果要优于一元线性回归模型的拟合效果.
方案一:通过比较残差的绝对值之和来比较两个模型的效果.
探索新知
方案三:通过比较决定系数R2来比较两个模型的效果.
残差平方和
总偏差平方和
(与回归方程无关)
(与回归方程有关)
R2越大,残差平方和越小,模型拟合效果越好.
经验回归方程②的刻画效果比经验回归方程①的好很多.
①R2越大,R2越接近1,残差平方和越小,模型拟合效果越好.
②样本相关系数r刻画线性相关关系的正负和强弱;
决定系数R2刻画模型拟合效果的好坏.
知识归纳
例:近期,某公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每天使用扫码支付的人次,用x表示活动推出的天数,y表示每天使用扫码支付的人次(单位:十人次),绘制了如图所示的散点图.
学以致用
(1)根据散点图判断在推广期内,y=a+bx与y=c·dx(c,d为大于0的常数)哪一个适宜作为每天使用扫码支付的人次y关于活动推出天数x的回归方程类型?(给出判断即可,不必说明理由)
【解】根据散点图判断,y=c·dx适宜作为每天使用扫码支付的人次y关于活动推出天数x的回归方程类型.
学以致用
(2)根据(1)的判断结果求y关于x的经验回归方程,并预测活动推出第8天使用扫码支付的人次.参考数据:其中v=lg y,
学以致用
解决非线性回归问题的方法及步骤
知识归纳
评价反馈
评价反馈
评价反馈
评价反馈
评价反馈
(3)当x=40时,y=≈1 131.
在使用经验回归方程进行预测时,需要注意下列问题:
(1) 经验回归方程只适用于所研究的样本的总体. 例如,根据我国父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述美国父亲身高与儿子身高之间的关系.同样,根据生长在南方多雨地区的树高与胸径的数据建立的经验回归方程,不能用来描述北方干旱地区的树高与胸径之间的关系.
(2) 经验回归方程一般都有时效性. 例如,根据20世纪80年代的父亲身高与儿子身高的数据建立的经验回归方程,不能用来描述现在的父亲身高与儿子身高之间的关系.
(3) 解释变量的取值不能离样本数据的范围太远. 一般解释变量的取值在样本数据范围内,经验回归方程的预报效果会比较好,超出这个范围越远,预报的效果越差.
(4) 不能期望经验回归方程得到的预报值就是响应变量的精确值. 事实上,它是响应变量的可能取值的平均值.
课堂小结
课堂小结
1.解决非线性经验回归问题的方法及步骤
2.决定系数R2
显然0≤R2≤1,R2越接近1,则模型拟合的效果越好.
谢谢大家
