第六章 章末复习--人教A版高中数学选择性必修第三册教学课件(共18张PPT)
文档属性
| 名称 | 第六章 章末复习--人教A版高中数学选择性必修第三册教学课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1008.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:28:31 | ||
图片预览





文档简介
(共18张PPT)
章节小结
第六章 计数原理
数学
学习目标
①能通过对本章知识的梳理与回顾,建构本章知识体系.
②能用自己的语言解释两个计数原理、排列、组合的内涵,能推导排列数公式、组合数公式及二项式定理.
③能用计数原理、排列与组合解决综合问题.
④能用二项式定理解决综合问题,提升数学运算素养.
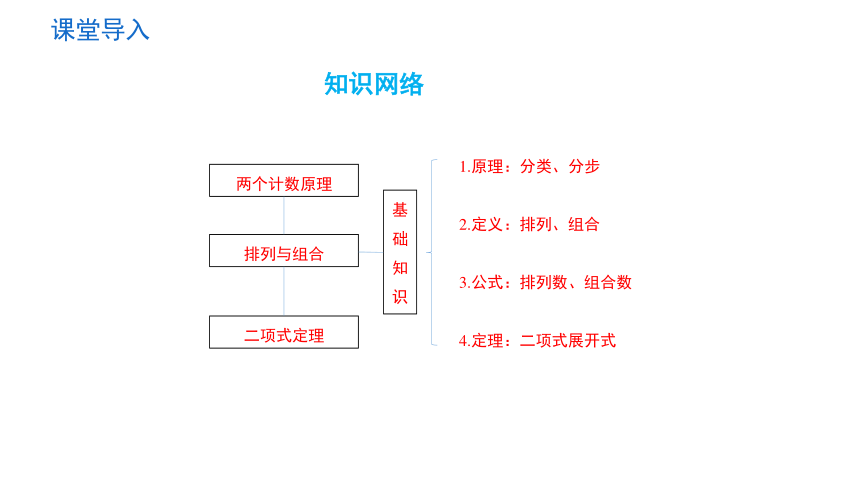
知识网络
两个计数原理
排列与组合
二项式定理
基
础
知
识
1.原理:分类、分步
2.定义:排列、组合
3.公式:排列数、组合数
4.定理:二项式展开式
课堂导入
环节一 自主研学,反思总结
问题1 阅读教科书第36~37页的小结内容,回顾本章的知识、思想与方法,你能回答第37页的5个问题吗?你能尝试自己画出本章知识结构图吗?
课堂探究
问题2 在数学学习中,举例是理解一般原理的好方法.你能再举几个应用两个计数原理的例子吗?你觉得在分类和分步时需要注意什么?
环节二 合作探究,归纳思想
课堂探究
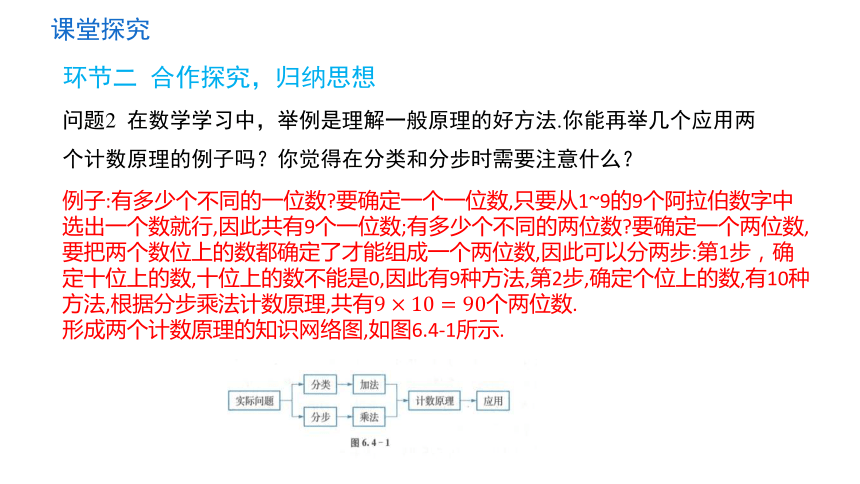
例子:有多少个不同的一位数 要确定一个一位数,只要从1~9的9个阿拉伯数字中选出一个数就行,因此共有9个一位数;有多少个不同的两位数 要确定一个两位数,要把两个数位上的数都确定了才能组成一个两位数,因此可以分两步:第1步,确定十位上的数,十位上的数不能是0,因此有9种方法,第2步,确定个位上的数,有10种方法,根据分步乘法计数原理,共有个两位数.
形成两个计数原理的知识网络图,如图6.4-1所示.
课堂探究
追问 你能总结分类加法计数原理与分步乘法计数原理的区别与联系吗
名称 分类加法计数原理 分步乘法计数原理
联系 都是完成一件事情的不同方法的种数问题 区别 1.完成一件事情有类方法,关键是分类;2.每一类方法都能完成相应的事情 1.完成一件事情有个步骤,关键是分步;
2.每一个步骤都相互依存,只有完成每一个步骤,才能完成相应的事情
问题3 加强数学知识间的联系,是深入理解知识的重要方法.例如,把本章的知识与集合有关的内容联系起来,可以简洁地表述有关原理.你能举例说明吗?
课堂探究
组合问题中元素的互异性与无序性对应集合元素的互异性与无序性.如果从集合的角度来考虑,那么分类加法计数原理表明了这样一个事实:将集合分成一些两两不交的子集而且的元素个数分别为那么集合的元素个数.从分类加法计数原理、组合和二项式定理的角度推导含有个元素的集合的子集个数,按照子集元素个数分类,可以分为含有个元素的类子集,集合元素具备互异性和无序性,因此含有个元素的子集个数就是从个不同元素中取出个元素的组合数结合分类加法计数原理和二项式定理,含有个元素的集合共有个子集.
问题4 排列、组合是特殊的计数问题,你能举例说明特殊在哪些方面吗?
课堂探究
排列的特殊性在于排列中元素的“互异性”和“有序性”,组合的特殊性在于它只有元素的“互异性”而不需要考虑顺序.排列与组合之间有紧密联系,从个不同元素中取出个元素的组合可以看成是相应排列的第一个步骤.
课堂探究
追问1 结合上述分析,你能说出排列与组合的区别与联系吗
名称 排列 组合
联系 都是从个不同元素中取出个不同元素,即取出的元素具有“互异性” 区别 取出的元素再按一定顺序排列,即“有序性” 取出的元素不再考虑顺序,即“无序性”
追问2 你能写出排列数公式和组合数公式吗
排列数公式:
组合数公式:.
课堂探究
课堂探究
问题5 回顾运用计数原理和组合知识推导二项式定理的过程,你有哪些体会 和小组里的同学交流一下.
明确二项式定理的推导是从特殊的和到一般的把的展开相乘看作次选取,每次有或两种选择,因此展开式中的每一项都是的形式.利用分步乘法计数原理可知,合并同类项之前共有项,每一项都可以看作是在个中恰好有个取得到的,从而同类项的系数为得到二项式展开式的通项以及二项式定理.
课堂探究
问题6 请你回顾本章的学习过程,结合具体知识,如计数原理、排列数公式、组合数公式或二项式定理,谈谈这些知识是如何抽象出来的?其中用到的思想方法主要有哪些?
环节三 例题练习,提高技能
课堂探究
例1 集合A含有1,2,3,4,5五个元素.
(1)由集合A中的元素可以组成多少个无重复数字的两位数?
(2)集合A含有2个元素的子集共有多少个?
(3)集合A中的元素可以组成多少个无重复数字的数?
课堂探究
方法一:5个元素中,任选2个可组成一个两位数,用树状图列举如下.
由树状图可知,共组成20个无重复数字的两位数
方法二:从5个不同的数中选出2个组成无重复数字的两位数,即从5个不同元素中任取2个元素的排列,因此可以组成个无重复数字的两位数.
(2)方法一:含2个元素的子集列举如下:共10个不同的子集.
方法二:5个元素的集合含有2个元素的子集,由于集合中元素的无序性,即从5个不同的元素中任取2个元素的组合,因此可以组成个不同的子集.
(3)若选1个元素,则可组成个不同的一位数;
若选2个元素,则可组成个不同的两位数;
若选3个元素,则可组成个不同的三位数;
若选4个元素,则可组成个不同的四位数;
若选5个元素,则可组成个不同的五位数.
因此,从5个元素中任意选取元素,可组成个无重复数字的数.
课堂探究
例2 已知的展开式中各二项式系数的和为32.
(1)求展开式中二项式系数最大的项;
(2)求展开式中各项系数的和.
解(1)由二项式系数的增减性和对称性可知,第3、4项的二项式系数最大,展开式的通项为则故二项式系数最大的项为.
(2)设各项系数为令则即展开式中各项系数的和为.
请你带着下列问题回顾本课内容,并给出回答:
(1)本章涉及哪些核心知识和公式?
(2)本章核心概念的产生、公式的推导采用了哪些基本思想与方法?
(3)应用两个计数原理和排列、组合知识应该注意什么?
课堂小结
教科书第37~38页复习参考题6第1,3,4,5题.
布置作业
谢谢大家
章节小结
第六章 计数原理
数学
学习目标
①能通过对本章知识的梳理与回顾,建构本章知识体系.
②能用自己的语言解释两个计数原理、排列、组合的内涵,能推导排列数公式、组合数公式及二项式定理.
③能用计数原理、排列与组合解决综合问题.
④能用二项式定理解决综合问题,提升数学运算素养.
知识网络
两个计数原理
排列与组合
二项式定理
基
础
知
识
1.原理:分类、分步
2.定义:排列、组合
3.公式:排列数、组合数
4.定理:二项式展开式
课堂导入
环节一 自主研学,反思总结
问题1 阅读教科书第36~37页的小结内容,回顾本章的知识、思想与方法,你能回答第37页的5个问题吗?你能尝试自己画出本章知识结构图吗?
课堂探究
问题2 在数学学习中,举例是理解一般原理的好方法.你能再举几个应用两个计数原理的例子吗?你觉得在分类和分步时需要注意什么?
环节二 合作探究,归纳思想
课堂探究
例子:有多少个不同的一位数 要确定一个一位数,只要从1~9的9个阿拉伯数字中选出一个数就行,因此共有9个一位数;有多少个不同的两位数 要确定一个两位数,要把两个数位上的数都确定了才能组成一个两位数,因此可以分两步:第1步,确定十位上的数,十位上的数不能是0,因此有9种方法,第2步,确定个位上的数,有10种方法,根据分步乘法计数原理,共有个两位数.
形成两个计数原理的知识网络图,如图6.4-1所示.
课堂探究
追问 你能总结分类加法计数原理与分步乘法计数原理的区别与联系吗
名称 分类加法计数原理 分步乘法计数原理
联系 都是完成一件事情的不同方法的种数问题 区别 1.完成一件事情有类方法,关键是分类;2.每一类方法都能完成相应的事情 1.完成一件事情有个步骤,关键是分步;
2.每一个步骤都相互依存,只有完成每一个步骤,才能完成相应的事情
问题3 加强数学知识间的联系,是深入理解知识的重要方法.例如,把本章的知识与集合有关的内容联系起来,可以简洁地表述有关原理.你能举例说明吗?
课堂探究
组合问题中元素的互异性与无序性对应集合元素的互异性与无序性.如果从集合的角度来考虑,那么分类加法计数原理表明了这样一个事实:将集合分成一些两两不交的子集而且的元素个数分别为那么集合的元素个数.从分类加法计数原理、组合和二项式定理的角度推导含有个元素的集合的子集个数,按照子集元素个数分类,可以分为含有个元素的类子集,集合元素具备互异性和无序性,因此含有个元素的子集个数就是从个不同元素中取出个元素的组合数结合分类加法计数原理和二项式定理,含有个元素的集合共有个子集.
问题4 排列、组合是特殊的计数问题,你能举例说明特殊在哪些方面吗?
课堂探究
排列的特殊性在于排列中元素的“互异性”和“有序性”,组合的特殊性在于它只有元素的“互异性”而不需要考虑顺序.排列与组合之间有紧密联系,从个不同元素中取出个元素的组合可以看成是相应排列的第一个步骤.
课堂探究
追问1 结合上述分析,你能说出排列与组合的区别与联系吗
名称 排列 组合
联系 都是从个不同元素中取出个不同元素,即取出的元素具有“互异性” 区别 取出的元素再按一定顺序排列,即“有序性” 取出的元素不再考虑顺序,即“无序性”
追问2 你能写出排列数公式和组合数公式吗
排列数公式:
组合数公式:.
课堂探究
课堂探究
问题5 回顾运用计数原理和组合知识推导二项式定理的过程,你有哪些体会 和小组里的同学交流一下.
明确二项式定理的推导是从特殊的和到一般的把的展开相乘看作次选取,每次有或两种选择,因此展开式中的每一项都是的形式.利用分步乘法计数原理可知,合并同类项之前共有项,每一项都可以看作是在个中恰好有个取得到的,从而同类项的系数为得到二项式展开式的通项以及二项式定理.
课堂探究
问题6 请你回顾本章的学习过程,结合具体知识,如计数原理、排列数公式、组合数公式或二项式定理,谈谈这些知识是如何抽象出来的?其中用到的思想方法主要有哪些?
环节三 例题练习,提高技能
课堂探究
例1 集合A含有1,2,3,4,5五个元素.
(1)由集合A中的元素可以组成多少个无重复数字的两位数?
(2)集合A含有2个元素的子集共有多少个?
(3)集合A中的元素可以组成多少个无重复数字的数?
课堂探究
方法一:5个元素中,任选2个可组成一个两位数,用树状图列举如下.
由树状图可知,共组成20个无重复数字的两位数
方法二:从5个不同的数中选出2个组成无重复数字的两位数,即从5个不同元素中任取2个元素的排列,因此可以组成个无重复数字的两位数.
(2)方法一:含2个元素的子集列举如下:共10个不同的子集.
方法二:5个元素的集合含有2个元素的子集,由于集合中元素的无序性,即从5个不同的元素中任取2个元素的组合,因此可以组成个不同的子集.
(3)若选1个元素,则可组成个不同的一位数;
若选2个元素,则可组成个不同的两位数;
若选3个元素,则可组成个不同的三位数;
若选4个元素,则可组成个不同的四位数;
若选5个元素,则可组成个不同的五位数.
因此,从5个元素中任意选取元素,可组成个无重复数字的数.
课堂探究
例2 已知的展开式中各二项式系数的和为32.
(1)求展开式中二项式系数最大的项;
(2)求展开式中各项系数的和.
解(1)由二项式系数的增减性和对称性可知,第3、4项的二项式系数最大,展开式的通项为则故二项式系数最大的项为.
(2)设各项系数为令则即展开式中各项系数的和为.
请你带着下列问题回顾本课内容,并给出回答:
(1)本章涉及哪些核心知识和公式?
(2)本章核心概念的产生、公式的推导采用了哪些基本思想与方法?
(3)应用两个计数原理和排列、组合知识应该注意什么?
课堂小结
教科书第37~38页复习参考题6第1,3,4,5题.
布置作业
谢谢大家
