第七章 7.2 离散型随机变量及其分布列--人教A版高中数学选择性必修第三册教学课件(共18张PPT)
文档属性
| 名称 | 第七章 7.2 离散型随机变量及其分布列--人教A版高中数学选择性必修第三册教学课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:28:45 | ||
图片预览






文档简介
(共18张PPT)
7.2 离散型随机变量及其分布列
第七章 随机变量及其分布
数学
学习目标
①借助教材实例,了解离散型随机变量的概念.
②通过实例,理解离散型随机变量分布列的概念.
③会求简单的离散型随机变量分布列.
④通过实例,理解两点分布.
课堂导入
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题.类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
问题1 有些随机试验的样本空间与数值有关系,我们可以直接与实数建立关系.
实例1.掷一枚骰子,设“掷出的点数为m”,则样本空间Ω={ }
实例2.掷两枚骰子,设“点数之和为m”,样本空间为Ω={ },
问题2 有些随机试验的样本空间与数值没有直接关系,可以根据问题的需要为每个样本点指定一个数值.
实例3.随机抽取一件产品,有“抽到次品”和“抽到正品”两种可能结果它们与数值无关.如果“抽到次品”用1表示,“抽到正品”用0表示,X=
实例4.掷一枚硬币,可将试验结果“正面朝上”用1表示,“反面朝上”用0表示,则样本空间Ω={ }.
实例5.随机调查一名学生的体育综合测试成绩,可将等级成绩优、良、中等、及格、不及格分别赋值5,4,3,2,1,则样本空间Ω={ }.
课堂探究
1,2,3,4,5,6
(x,y)|x,y=1,2,…,6
0
1
0,1
1,2,3,4,5
概念形成
问题3 考察下列随机试验及其引入的变量:
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验,变量X 表示三个元件中次品数;
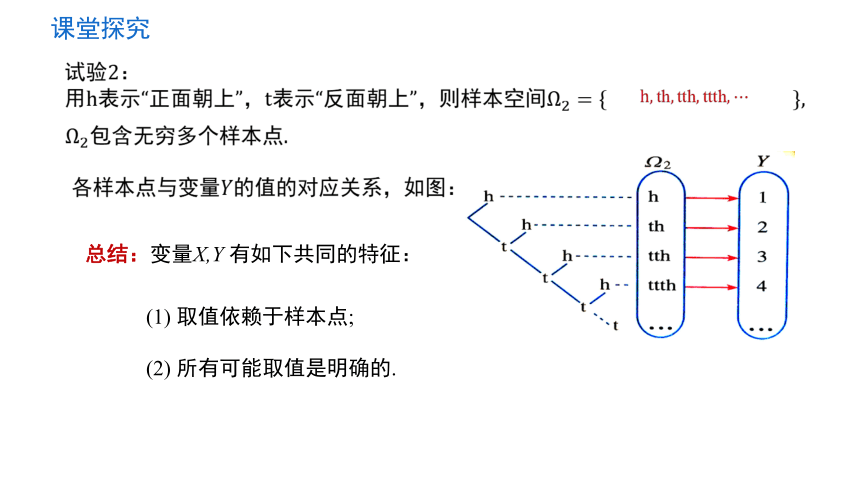
试验2:抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么
各个样本点与变量的值是如何对应的
变量X,Y有哪些共同的特征
试验1:
用0表示“元件为合格品”,1表示“元件为次品”,用0和1构成的长度为3
的字符串表示样本点,则样本空间Ω1={ },
课堂探究
000,001,010,100,011,101,110,111
总结:变量X,Y 有如下共同的特征:
(1) 取值依赖于样本点;
(2) 所有可能取值是明确的.
课堂探究
概念形成
可能取值为有限个或可以一一列举的随机变量,我们称之为离散型随机变量.
通常用大写英文字母表示随机变量,例如X,Y,Z;
用小写英文字母表示随机变量的取值,例如x,y,z.
课堂探究
概念理解
1.随机变量的定义与函数的定义类似
(1)相同点:样本点ω相当于函数定义中的自变量,而样本空间Ω相当于函数的定义域;
(2)不相同点:样本空间Ω不一定是数集.
2.不是离散型的随机变量是指可能取值充满了某个区间、不能一一列举的随机变量.
课堂探究
问题4 抛掷一枚骰子,所得的点数X有哪些值?取每个值的概率是多少?
X的取值我们可以用以下三种方法表示:
1.解析式法:P(X=m)=,m=1,2,…,6.
2.表格法:
X 1 2 3 4 5 6
P
3.图象法:
课堂探究
一般地,设离散型随机变量X可能取值为x1,x2,…,xi,…,xn,我们称X取每一个值xi的概率
P(X=xi)=pi, i=1,2,…,n
为X的概率分布列,简称为分布列.
离散型随机变量分布列的性质:
课堂探究
①pi≥0(i=1,2,…,n);
②npi=1.
例1 一批产品中次品率为5%,随机抽取1件,定义X=
求X的分布列.
X 0 1
P 0.95 0.05
若随机变量X的分布列为
X 0 1
P 1-p p
则称X服从两点分布列或0-1分布.
课堂探究
例题解析
例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如下表所示.
等级 不及格 及格 中等 良 优
分数 1 2 3 4 5
人数 20 50 60 40 30
根据古典概型的知识,可得X的分布列,如下表所示.
X 1 2 3 4 5
P
课堂探究
P(X≥4)=P(X=4)+P(X=5)==.
从这200名学生中任意选取1人,求所选同学分数X的分布列,以及.
例3 一批笔记本电脑共有10台,其中A品牌3台 ,B品牌7台.如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.
解 设挑选的2台电脑中A品牌的台数为X,则X的可能取值为0,1,2.根据古典概型的知识,可得X的分布列为
P(X=0)==,P(X=1)==,P(X=2)==.
用表格表示X的分布列为
X 0 1 2
P
课堂探究
2.下列随机变量中不是离散型随机变量的是________.(填序号)
①某机场候机室中一天的旅客数量X; ②某水文站观察到一天中珠江的水位X;
③某景点一日接待游客的数量X; ④某大桥上一天经过的车辆数X.
②
1.离散型随机变量X的分布列中部分数据丢失,丢失数据以x,y(x,y∈N)代替,分布列如下:
则P(2≤X≤3)等于( )
A. 0.25 B. 0.35 C. 0.45 D. 0.55
B
评价反馈
X 1 2 3 4 5 6
P 0.20 0.10 0.x5 0.10 0.1y 0.20
3.设随机变量X的分布列P(X= )=ak,(k=1,2,3,4,5).
(1)求常数a的值;(2)求;(3)求P(<X< ).
解 由题意,所给分布列为
(1)由分布列的性质得a+2a+3a+4a+5a=1,解得a= .
评价反馈
X
P a 2a 3a 4a 5a
(2)
.
(3)
课堂小结
1.随机变量:
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量.
2.离散型随机变量:
可能取值为有限个或可以一一列举的随机变量,称之为离散型随机变量.
特点:①取值依赖于样本点; ②所有可能取值是明确的.
表示:通常用大写英文字母表示随机变量,例如 X,Y,Z; 用小写英文字母表示随机变量的取值,例如,,.
意义:为一些随机事件及其样本空间的表示带来方便,且能更好地利用数学工具研究随机试验的概率问题.
3.离散型随机变量的概率分布列及性质.
布置作业
教科书第60~61页习题.
谢谢大家
7.2 离散型随机变量及其分布列
第七章 随机变量及其分布
数学
学习目标
①借助教材实例,了解离散型随机变量的概念.
②通过实例,理解离散型随机变量分布列的概念.
③会求简单的离散型随机变量分布列.
④通过实例,理解两点分布.
课堂导入
求随机事件的概率时,我们往往需要为随机试验建立样本空间,并会涉及样本点和随机事件的表示问题.类似函数在数集与数集之间建立对应关系,如果我们在随机试验的样本空间与实数集之间建立某种对应,将不仅可以为一些随机事件的表示带来方便,而且能更好地利用数学工具研究随机试验.
问题1 有些随机试验的样本空间与数值有关系,我们可以直接与实数建立关系.
实例1.掷一枚骰子,设“掷出的点数为m”,则样本空间Ω={ }
实例2.掷两枚骰子,设“点数之和为m”,样本空间为Ω={ },
问题2 有些随机试验的样本空间与数值没有直接关系,可以根据问题的需要为每个样本点指定一个数值.
实例3.随机抽取一件产品,有“抽到次品”和“抽到正品”两种可能结果它们与数值无关.如果“抽到次品”用1表示,“抽到正品”用0表示,X=
实例4.掷一枚硬币,可将试验结果“正面朝上”用1表示,“反面朝上”用0表示,则样本空间Ω={ }.
实例5.随机调查一名学生的体育综合测试成绩,可将等级成绩优、良、中等、及格、不及格分别赋值5,4,3,2,1,则样本空间Ω={ }.
课堂探究
1,2,3,4,5,6
(x,y)|x,y=1,2,…,6
0
1
0,1
1,2,3,4,5
概念形成
问题3 考察下列随机试验及其引入的变量:
试验1:从100个电子元件(至少含3个以上次品)中随机抽取三个进行试验,变量X 表示三个元件中次品数;
试验2:抛掷一枚硬币直到出现正面为止,变量Y 表示需要的抛掷次数.
这两个随机试验的样本空间各是什么
各个样本点与变量的值是如何对应的
变量X,Y有哪些共同的特征
试验1:
用0表示“元件为合格品”,1表示“元件为次品”,用0和1构成的长度为3
的字符串表示样本点,则样本空间Ω1={ },
课堂探究
000,001,010,100,011,101,110,111
总结:变量X,Y 有如下共同的特征:
(1) 取值依赖于样本点;
(2) 所有可能取值是明确的.
课堂探究
概念形成
可能取值为有限个或可以一一列举的随机变量,我们称之为离散型随机变量.
通常用大写英文字母表示随机变量,例如X,Y,Z;
用小写英文字母表示随机变量的取值,例如x,y,z.
课堂探究
概念理解
1.随机变量的定义与函数的定义类似
(1)相同点:样本点ω相当于函数定义中的自变量,而样本空间Ω相当于函数的定义域;
(2)不相同点:样本空间Ω不一定是数集.
2.不是离散型的随机变量是指可能取值充满了某个区间、不能一一列举的随机变量.
课堂探究
问题4 抛掷一枚骰子,所得的点数X有哪些值?取每个值的概率是多少?
X的取值我们可以用以下三种方法表示:
1.解析式法:P(X=m)=,m=1,2,…,6.
2.表格法:
X 1 2 3 4 5 6
P
3.图象法:
课堂探究
一般地,设离散型随机变量X可能取值为x1,x2,…,xi,…,xn,我们称X取每一个值xi的概率
P(X=xi)=pi, i=1,2,…,n
为X的概率分布列,简称为分布列.
离散型随机变量分布列的性质:
课堂探究
①pi≥0(i=1,2,…,n);
②npi=1.
例1 一批产品中次品率为5%,随机抽取1件,定义X=
求X的分布列.
X 0 1
P 0.95 0.05
若随机变量X的分布列为
X 0 1
P 1-p p
则称X服从两点分布列或0-1分布.
课堂探究
例题解析
例2 某学校高二年级有200名学生,他们的体育综合测试成绩分5个等级,每个等级对应的分数和人数如下表所示.
等级 不及格 及格 中等 良 优
分数 1 2 3 4 5
人数 20 50 60 40 30
根据古典概型的知识,可得X的分布列,如下表所示.
X 1 2 3 4 5
P
课堂探究
P(X≥4)=P(X=4)+P(X=5)==.
从这200名学生中任意选取1人,求所选同学分数X的分布列,以及.
例3 一批笔记本电脑共有10台,其中A品牌3台 ,B品牌7台.如果从中随机挑选2台,求这2台电脑中A品牌台数的分布列.
解 设挑选的2台电脑中A品牌的台数为X,则X的可能取值为0,1,2.根据古典概型的知识,可得X的分布列为
P(X=0)==,P(X=1)==,P(X=2)==.
用表格表示X的分布列为
X 0 1 2
P
课堂探究
2.下列随机变量中不是离散型随机变量的是________.(填序号)
①某机场候机室中一天的旅客数量X; ②某水文站观察到一天中珠江的水位X;
③某景点一日接待游客的数量X; ④某大桥上一天经过的车辆数X.
②
1.离散型随机变量X的分布列中部分数据丢失,丢失数据以x,y(x,y∈N)代替,分布列如下:
则P(2≤X≤3)等于( )
A. 0.25 B. 0.35 C. 0.45 D. 0.55
B
评价反馈
X 1 2 3 4 5 6
P 0.20 0.10 0.x5 0.10 0.1y 0.20
3.设随机变量X的分布列P(X= )=ak,(k=1,2,3,4,5).
(1)求常数a的值;(2)求;(3)求P(<X< ).
解 由题意,所给分布列为
(1)由分布列的性质得a+2a+3a+4a+5a=1,解得a= .
评价反馈
X
P a 2a 3a 4a 5a
(2)
.
(3)
课堂小结
1.随机变量:
一般地,对于随机试验样本空间Ω中的每个样本点ω,都有唯一的实数X(ω)与之对应,我们称X为随机变量.
2.离散型随机变量:
可能取值为有限个或可以一一列举的随机变量,称之为离散型随机变量.
特点:①取值依赖于样本点; ②所有可能取值是明确的.
表示:通常用大写英文字母表示随机变量,例如 X,Y,Z; 用小写英文字母表示随机变量的取值,例如,,.
意义:为一些随机事件及其样本空间的表示带来方便,且能更好地利用数学工具研究随机试验的概率问题.
3.离散型随机变量的概率分布列及性质.
布置作业
教科书第60~61页习题.
谢谢大家
