第七章 7.3.1离散型随机变量的均值--人教A版高中数学选择性必修第三册课件(共22张PPT)
文档属性
| 名称 | 第七章 7.3.1离散型随机变量的均值--人教A版高中数学选择性必修第三册课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 356.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:28:54 | ||
图片预览






文档简介
(共22张PPT)
第七章 随机变量及其分布
数学
7.3.1 离散型随机变量的均值
学习目标
①通过实例理解离散型随机变量的均值(数学期望)的概念和性质.
②能在具体事例中,根据离散型随机变量的分布列求出均值.
③会利用离散型随机变量的均值解决一些相关的实际问题,并进行决策选择.
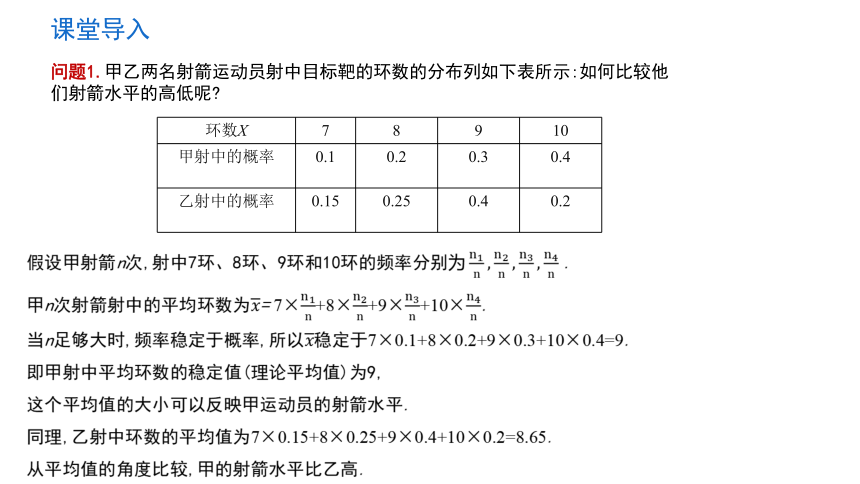
问题1.甲乙两名射箭运动员射中目标靶的环数的分布列如下表所示:如何比较他们射箭水平的高低呢
环数X 7 8 9 10
甲射中的概率 0.1 0.2 0.3 0.4
乙射中的概率 0.15 0.25 0.4 0.2
课堂导入
假设甲射箭n次,射中7环、8环、9环和10环的频率分别 .
甲n次射箭射中的平均环数为= 7×+8×+9×+10×.
当n足够大时,频率稳定于概率,所以稳定于7×0.1+8×0.2+9×0.3+10×0.4=9.
即甲射中平均环数的稳定值(理论平均值)为9,
这个平均值的大小可以反映甲运动员的射箭水平.
同理,乙射中环数的平均值为7×0.15+8×0.25+9×0.4+10×0.2=8.65.
从平均值的角度比较,甲的射箭水平比乙高.
概念形成
1.随机变量X的均值:
一般地,若离散型随机变量X的概率分布为:
X x1 x2 ... xi ... xn
P p1 p2 ... pi ... pn
均值是随机变量可能取值关于取值概率的加权平均数.
它综合了随机变量的取值和取值的概率,反映了随机变量取值的平均水平.
课堂探究
例题解析
例1 在篮球比赛中,罚球命中1次得1分,不中得0分,如果某运动员罚球命中的概率为0.8,那么他罚球1次的得分X的均值是多少
解:因为P(X=1)=0.8,P(X=0)=0.2,
所以E(X)=1×P(X=1)+0×P(X=0)=1×0.8+0×0.2 =0.8.
即该运动员罚球1次的得分X的均值是0.8.
课堂探究
一般地,如果随机变量X服从两点分布,
X 1 0
P p 1-p
那么E(X)=1×p+0×(1-p)=p.
课堂探究
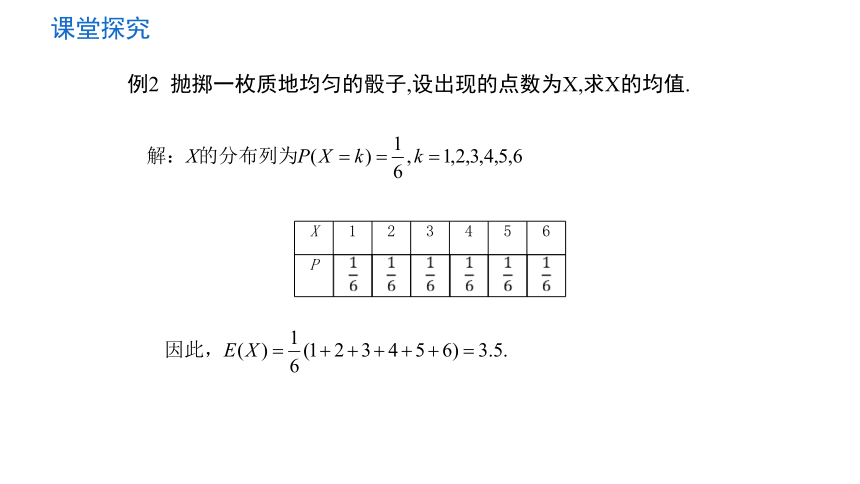
例2 抛掷一枚质地均匀的骰子,设出现的点数为X,求X的均值.
X 1 2 3 4 5 6
P
课堂探究
方法总结
求离散型随机变量X的均值的步骤:
(1)理解X的实际意义,写出X的全部可能取值;
(2)求出X取每个值时的概率;
(3)写出X的分布列(有时也可省略);
(4)利用定义公式 求出均值.
课堂探究
变式练习
1.随机抛掷一个正四面体,正四面体每个面分别标号1,2,3,4,
求:朝下一面标号X的均值.
X 1 2 3 4
P
课堂探究
问题2.
如果X是一个离散型随机变量,X加一个常数或乘一个常数后,其均值会怎样变化 即E(X+b)和E(aX)(其中a,b为常数)分别与E(X)由怎样的关系?
随机变量X,X+b,aX的分布列如下表:
X x1 x2 ... xi ... xn
X+b x1+b x2+b ... xi+b ... xn+b
aX ax1 ax2 ... axi ... axn
P p1 p2 ... pi ... pn
课堂探究
所以E(X+b)=(x1+b)p1+(x2+b)p2+...+(xi+b)pi+...+(xn+b)pn
=(x1p1+x2p2+...+xipi+...+xnpn)+bp1+bp2+...bpi+...+bpn
=E(X)+b.
同理,E(aX)=aE(X).
课堂探究
一般地,E(aX+b)=aE(X)+b.
例3 猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名.某嘉宾参加猜歌名节目,猜对每首歌曲的歌名相互独立,猜对三首歌曲A , B , C歌名的概率及猜对时获得相应的公益基金如下表所示:
歌曲 A B C
猜对的概率 0.8 0.6 0.4
获得的公益基金额/元 1 000 2 000 3 000
规则如下:按照A , B , C的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额X的分布列及均值.
分析:根据规则,公益基金总额X的可能取值有四种情况:猜错A,获得0元基金;
猜对A而猜错B,获得1 000元基金;猜对A和B而猜错C,获得3 000元基金:A,B,
C全部猜对,获得6 000元基金.因此X是一个离散型随机变量.利用独立条件下的乘法公式可求分布列.
课堂探究
解:分别用A ,B,C表示猜对歌曲A,B,C歌名的事件,则A,B,C相互独立.
P(X=0)= P() =0.2,
P(X=1000)= P(A)=0.8×0.4=0.32,
P(X=3000)= P(AB)= 0.8×0.6×0.6=0.288,
P(X=6000)= P(ABC)=0.8×0.6×0.4=0.192.
X的分布列如下表所示.
X 0 1000 3000 6000
P 0.2 0.32 0.288 0.192
X的均值为
E(X)=0×0.2+1000×0.32+3000×0.288+6000×0.192=2 336.
课堂探究
思考1:如果改变猜歌的顺序,获得公益基金的均值是否相同 如果不同,你认为哪个顺序获得的公益基金均值最大
解:如果按A,C,B的顺序来猜歌,分别用A,B,C表示猜对歌曲A,B,C歌名的事件,
A,B,C相互独立;
P (X=0)= P() = 0.2, P (X=1 000)= P(A)= 0.8×0.6=0.48,
P(X=3000)= P(AB)= 0.8×0.4×0.4=0.128,
P (X=6000)= P(ABC)= 0.8×0.4×0.6=0.192.
X的分布列如下表所示:
X 0 1000 3000 6000
P 0.2 0.48 0.128 0.192
X的均值为E(X)=0×0.2+1000×0.48+3000×0.128+6000×0.192=2016.
课堂探究
猜歌顺序 E(X) 猜歌顺序 E(X)
ABC 2336 BCA 1656
ACB 2016 CAB 1616
BAC 2256 CBA 1456
故按ABC的顺序来猜歌,获得公益基金的均值最大.
课堂探究
同理,可得猜歌顺序按BAC、BCA、CAB、CBA的公益基金均值分别为2256,1656,1616,1456,则猜歌顺序与该顺序下获得公益基金均值对应表如下.
例4 根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60 000元,遇到小洪水时要损失10 000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3 800元.
方案2:建保护围墙,建设费为2 000元,但围墙只能挡小洪水.
方案3:不采取措施.
工地的领导该如何决策呢
分析:决策目标为总损失(投入费用与设备损失之和)越小越好,根据题意,各种方案在不同状态下的总损失如表所示.
天气状况 大洪水 小洪水 没有洪水
概率 0.01 0.25 0.74
总损失/元 方案1 3 800 3 800 3 800
方案2 62 000 2 000 2 000
方案3 60 000 10 000 0
方案2和方案3的总损失都是随机变量,可以采用期望总损失最小的方案.
课堂探究
解:设方案1、 方案2、方案3的总损失分别为X1,X2,X3.
采用方案1:
无论有无洪水,都损失3 800元.因此,P(X1=3 800)=1.
采用方案2:
遇到大洪水时,总损失为2 000+60 000 =62 000元;没有大洪水时,总损失为2 000元.
因此P(X2=62 000)=0.01, P(X2=2 000)=0.99.
采用方案3:
P(X3=60 000)=0.01 ,P(X3=10 000)=0.25, P(X3=0)=0.74.
于是,E(X1)=3 800,
E(X2)=62 000×0.01+2 000×0. 99=2 600,
E(X3)=60 000×0.01+10 000×0.25+0×0.74=3 100.
因此,从期望损失最小的角度,应采取方案2.
课堂探究
1.若随机变量X的分布列为
X -1 0 1
P
则E(X)=( )
A.0 B.-1 C. D.
C
2.某射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目X的均值为( )
A.2.44 B.3.376 C.2.376 D.2.4
解析:X的可能取值为3,2,1,0,则P(X=3)=0.6;P(X=2)=0.4×0.6=0.24; P(X=1)=0.42×0.6=0.096;
P(X=0)=0.43=0.064.所以E(X)=3×0.6+2×0.24+1×0.096+0×0.064=2.376.
3.已知X的分布列如下表,若Y=3X+2,则E(Y)= .
X 1 2 3
P t
评价反馈
C
4.某商场经销某商品,根据以往资料统计,顾客采用的付款期数X的分布列为
X 1 2 3 4 5
P 0.4 0.2 0.2 0.1 0.1
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元, Y表示经销一件该商品的利润.求Y的分布列及均值.
解:Y的可能取值为200 , 250 , 300.
P(Y= 200)=P(X= 1)= 0.4,
P(Y= 250)= P(X=2)+ P(X= 3)=0.2+ 0.2= 0.4,
P(Y= 300)=P(X=4)+ P(X=5)=0.l+0.l= 0.2,
因此Y的分布列为
Y 200 250 300
P 0.4 0.4 0.2
E(Y)= 200×0.4 + 250×0.4 + 300×0.2= 240.
评价反馈
5.在一个口袋里装有大小相同的8张卡片,其中3张标有数字1,3张标有数字2,2张标有数字3.第一次从口袋里任意抽取1张,放回口袋里后第二次再任意抽取1张,记第一次与第二次取到卡片上数字之和为X.求:
(1)X为何值时,其发生的概率最大 并说明理由.
(2)随机变量X的均值.
因为 P(X=5)=,P(X=6)=.
故当X=4时,其发生的概率最大.
评价反馈
1.求离散型随机变量均值的步骤
求离散型随机变量X的均值的步骤:
(1)理解X的实际意义,写出X的全部可能取值;
(2)求出X取每个值时的概率;
(3)写出X的分布列(有时也可省略);
(4)利用定义公式 求出均值.
2.若X,Y是两个随机变量,且Y=aX+b,
则E(Y)=aE(X)+b;
3.如果一个随机变量服从两点分布,可直接利用公式计算均值.
课堂小结
谢谢大家
第七章 随机变量及其分布
数学
7.3.1 离散型随机变量的均值
学习目标
①通过实例理解离散型随机变量的均值(数学期望)的概念和性质.
②能在具体事例中,根据离散型随机变量的分布列求出均值.
③会利用离散型随机变量的均值解决一些相关的实际问题,并进行决策选择.
问题1.甲乙两名射箭运动员射中目标靶的环数的分布列如下表所示:如何比较他们射箭水平的高低呢
环数X 7 8 9 10
甲射中的概率 0.1 0.2 0.3 0.4
乙射中的概率 0.15 0.25 0.4 0.2
课堂导入
假设甲射箭n次,射中7环、8环、9环和10环的频率分别 .
甲n次射箭射中的平均环数为= 7×+8×+9×+10×.
当n足够大时,频率稳定于概率,所以稳定于7×0.1+8×0.2+9×0.3+10×0.4=9.
即甲射中平均环数的稳定值(理论平均值)为9,
这个平均值的大小可以反映甲运动员的射箭水平.
同理,乙射中环数的平均值为7×0.15+8×0.25+9×0.4+10×0.2=8.65.
从平均值的角度比较,甲的射箭水平比乙高.
概念形成
1.随机变量X的均值:
一般地,若离散型随机变量X的概率分布为:
X x1 x2 ... xi ... xn
P p1 p2 ... pi ... pn
均值是随机变量可能取值关于取值概率的加权平均数.
它综合了随机变量的取值和取值的概率,反映了随机变量取值的平均水平.
课堂探究
例题解析
例1 在篮球比赛中,罚球命中1次得1分,不中得0分,如果某运动员罚球命中的概率为0.8,那么他罚球1次的得分X的均值是多少
解:因为P(X=1)=0.8,P(X=0)=0.2,
所以E(X)=1×P(X=1)+0×P(X=0)=1×0.8+0×0.2 =0.8.
即该运动员罚球1次的得分X的均值是0.8.
课堂探究
一般地,如果随机变量X服从两点分布,
X 1 0
P p 1-p
那么E(X)=1×p+0×(1-p)=p.
课堂探究
例2 抛掷一枚质地均匀的骰子,设出现的点数为X,求X的均值.
X 1 2 3 4 5 6
P
课堂探究
方法总结
求离散型随机变量X的均值的步骤:
(1)理解X的实际意义,写出X的全部可能取值;
(2)求出X取每个值时的概率;
(3)写出X的分布列(有时也可省略);
(4)利用定义公式 求出均值.
课堂探究
变式练习
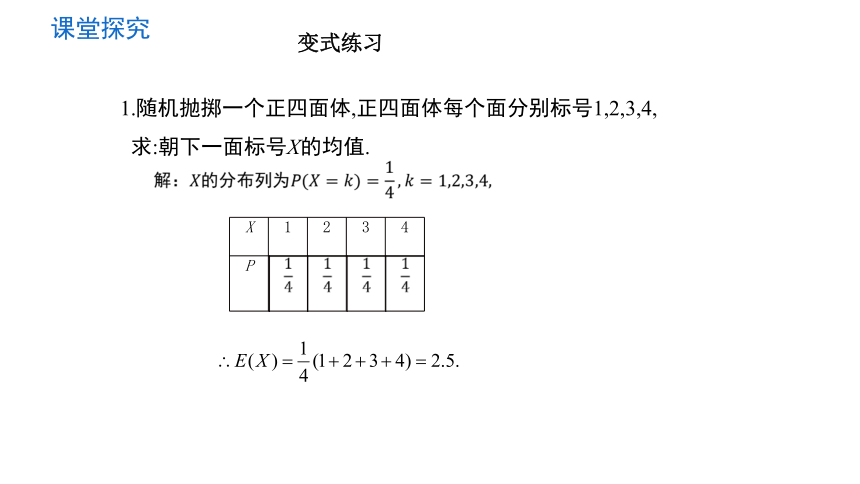
1.随机抛掷一个正四面体,正四面体每个面分别标号1,2,3,4,
求:朝下一面标号X的均值.
X 1 2 3 4
P
课堂探究
问题2.
如果X是一个离散型随机变量,X加一个常数或乘一个常数后,其均值会怎样变化 即E(X+b)和E(aX)(其中a,b为常数)分别与E(X)由怎样的关系?
随机变量X,X+b,aX的分布列如下表:
X x1 x2 ... xi ... xn
X+b x1+b x2+b ... xi+b ... xn+b
aX ax1 ax2 ... axi ... axn
P p1 p2 ... pi ... pn
课堂探究
所以E(X+b)=(x1+b)p1+(x2+b)p2+...+(xi+b)pi+...+(xn+b)pn
=(x1p1+x2p2+...+xipi+...+xnpn)+bp1+bp2+...bpi+...+bpn
=E(X)+b.
同理,E(aX)=aE(X).
课堂探究
一般地,E(aX+b)=aE(X)+b.
例3 猜歌名游戏是根据歌曲的主旋律制成的铃声来猜歌名.某嘉宾参加猜歌名节目,猜对每首歌曲的歌名相互独立,猜对三首歌曲A , B , C歌名的概率及猜对时获得相应的公益基金如下表所示:
歌曲 A B C
猜对的概率 0.8 0.6 0.4
获得的公益基金额/元 1 000 2 000 3 000
规则如下:按照A , B , C的顺序猜,只有猜对当前歌曲的歌名才有资格猜下一首,求嘉宾获得的公益基金总额X的分布列及均值.
分析:根据规则,公益基金总额X的可能取值有四种情况:猜错A,获得0元基金;
猜对A而猜错B,获得1 000元基金;猜对A和B而猜错C,获得3 000元基金:A,B,
C全部猜对,获得6 000元基金.因此X是一个离散型随机变量.利用独立条件下的乘法公式可求分布列.
课堂探究
解:分别用A ,B,C表示猜对歌曲A,B,C歌名的事件,则A,B,C相互独立.
P(X=0)= P() =0.2,
P(X=1000)= P(A)=0.8×0.4=0.32,
P(X=3000)= P(AB)= 0.8×0.6×0.6=0.288,
P(X=6000)= P(ABC)=0.8×0.6×0.4=0.192.
X的分布列如下表所示.
X 0 1000 3000 6000
P 0.2 0.32 0.288 0.192
X的均值为
E(X)=0×0.2+1000×0.32+3000×0.288+6000×0.192=2 336.
课堂探究
思考1:如果改变猜歌的顺序,获得公益基金的均值是否相同 如果不同,你认为哪个顺序获得的公益基金均值最大
解:如果按A,C,B的顺序来猜歌,分别用A,B,C表示猜对歌曲A,B,C歌名的事件,
A,B,C相互独立;
P (X=0)= P() = 0.2, P (X=1 000)= P(A)= 0.8×0.6=0.48,
P(X=3000)= P(AB)= 0.8×0.4×0.4=0.128,
P (X=6000)= P(ABC)= 0.8×0.4×0.6=0.192.
X的分布列如下表所示:
X 0 1000 3000 6000
P 0.2 0.48 0.128 0.192
X的均值为E(X)=0×0.2+1000×0.48+3000×0.128+6000×0.192=2016.
课堂探究
猜歌顺序 E(X) 猜歌顺序 E(X)
ABC 2336 BCA 1656
ACB 2016 CAB 1616
BAC 2256 CBA 1456
故按ABC的顺序来猜歌,获得公益基金的均值最大.
课堂探究
同理,可得猜歌顺序按BAC、BCA、CAB、CBA的公益基金均值分别为2256,1656,1616,1456,则猜歌顺序与该顺序下获得公益基金均值对应表如下.
例4 根据气象预报,某地区近期有小洪水的概率为0.25,有大洪水的概率为0.01,该地区某工地上有一台大型设备,遇到大洪水时要损失60 000元,遇到小洪水时要损失10 000元.为保护设备,有以下3种方案:
方案1:运走设备,搬运费为3 800元.
方案2:建保护围墙,建设费为2 000元,但围墙只能挡小洪水.
方案3:不采取措施.
工地的领导该如何决策呢
分析:决策目标为总损失(投入费用与设备损失之和)越小越好,根据题意,各种方案在不同状态下的总损失如表所示.
天气状况 大洪水 小洪水 没有洪水
概率 0.01 0.25 0.74
总损失/元 方案1 3 800 3 800 3 800
方案2 62 000 2 000 2 000
方案3 60 000 10 000 0
方案2和方案3的总损失都是随机变量,可以采用期望总损失最小的方案.
课堂探究
解:设方案1、 方案2、方案3的总损失分别为X1,X2,X3.
采用方案1:
无论有无洪水,都损失3 800元.因此,P(X1=3 800)=1.
采用方案2:
遇到大洪水时,总损失为2 000+60 000 =62 000元;没有大洪水时,总损失为2 000元.
因此P(X2=62 000)=0.01, P(X2=2 000)=0.99.
采用方案3:
P(X3=60 000)=0.01 ,P(X3=10 000)=0.25, P(X3=0)=0.74.
于是,E(X1)=3 800,
E(X2)=62 000×0.01+2 000×0. 99=2 600,
E(X3)=60 000×0.01+10 000×0.25+0×0.74=3 100.
因此,从期望损失最小的角度,应采取方案2.
课堂探究
1.若随机变量X的分布列为
X -1 0 1
P
则E(X)=( )
A.0 B.-1 C. D.
C
2.某射手对靶射击,直到第一次命中为止,每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目X的均值为( )
A.2.44 B.3.376 C.2.376 D.2.4
解析:X的可能取值为3,2,1,0,则P(X=3)=0.6;P(X=2)=0.4×0.6=0.24; P(X=1)=0.42×0.6=0.096;
P(X=0)=0.43=0.064.所以E(X)=3×0.6+2×0.24+1×0.096+0×0.064=2.376.
3.已知X的分布列如下表,若Y=3X+2,则E(Y)= .
X 1 2 3
P t
评价反馈
C
4.某商场经销某商品,根据以往资料统计,顾客采用的付款期数X的分布列为
X 1 2 3 4 5
P 0.4 0.2 0.2 0.1 0.1
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元, Y表示经销一件该商品的利润.求Y的分布列及均值.
解:Y的可能取值为200 , 250 , 300.
P(Y= 200)=P(X= 1)= 0.4,
P(Y= 250)= P(X=2)+ P(X= 3)=0.2+ 0.2= 0.4,
P(Y= 300)=P(X=4)+ P(X=5)=0.l+0.l= 0.2,
因此Y的分布列为
Y 200 250 300
P 0.4 0.4 0.2
E(Y)= 200×0.4 + 250×0.4 + 300×0.2= 240.
评价反馈
5.在一个口袋里装有大小相同的8张卡片,其中3张标有数字1,3张标有数字2,2张标有数字3.第一次从口袋里任意抽取1张,放回口袋里后第二次再任意抽取1张,记第一次与第二次取到卡片上数字之和为X.求:
(1)X为何值时,其发生的概率最大 并说明理由.
(2)随机变量X的均值.
因为 P(X=5)=,P(X=6)=.
故当X=4时,其发生的概率最大.
评价反馈
1.求离散型随机变量均值的步骤
求离散型随机变量X的均值的步骤:
(1)理解X的实际意义,写出X的全部可能取值;
(2)求出X取每个值时的概率;
(3)写出X的分布列(有时也可省略);
(4)利用定义公式 求出均值.
2.若X,Y是两个随机变量,且Y=aX+b,
则E(Y)=aE(X)+b;
3.如果一个随机变量服从两点分布,可直接利用公式计算均值.
课堂小结
谢谢大家
