第七章 7.3.2离散型随机变量的方差--人教A版高中数学选择性必修第三册教学课件(共24张PPT)
文档属性
| 名称 | 第七章 7.3.2离散型随机变量的方差--人教A版高中数学选择性必修第三册教学课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 619.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:35:29 | ||
图片预览






文档简介
(共24张PPT)
7.3.2 离散型随机变量的方差
第七章 随机变量及其分布
数学
学习目标
①通过具体实例,理解取有限值的离散型随机变量的方差、标准差的含义.
②能计算简单离散型随机变量的方差,并能解决一些实际问题.
③掌握方差的性质以及两点分布的方差的求法.
课堂导入
随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.
因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.
所以我们还需要寻找反映随机变量取值波动大小的数字特征.
问题1 从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列如下表所示.
如何评价这两名同学的射击水平
X 6 7 8 9 10
P 0.09 0.24 0.32 0.28 0.07
Y 6 7 8 9 10
P 0.07 0.22 0.38 0.30 0.03
通过计算可得
评价射击水平,除了要了解击中环数的均值外,还要考虑稳定性,即击中环数的离散程度.
E(X)= 8 ;E(Y)=8
由于E(X)=E(Y),所以根据均值不能区分这两名同学的射击水平.
课堂探究
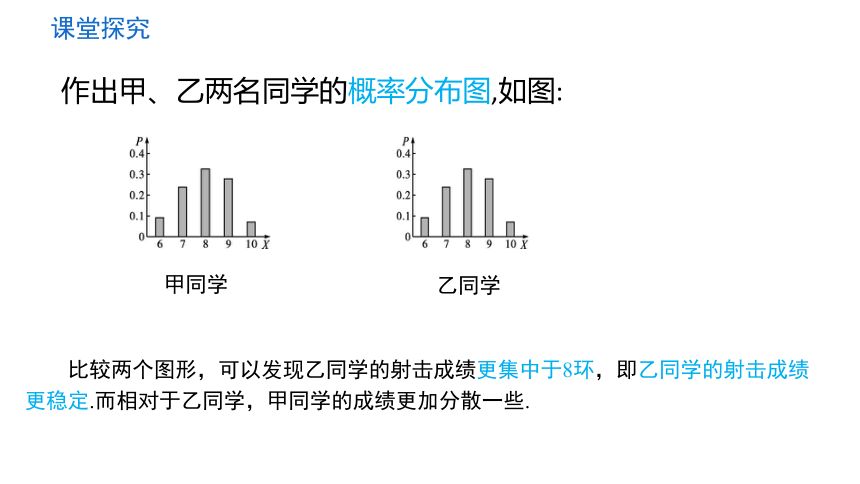
作出甲、乙两名同学的概率分布图,如图:
比较两个图形,可以发现乙同学的射击成绩更集中于8环,即乙同学的射击成绩更稳定.而相对于乙同学,甲同学的成绩更加分散一些.
课堂探究
甲同学
乙同学
样本的离散程度是用哪个量刻画的?
样本方差
随机变量 X 的方差
能否用一个与样本方差类似的量来刻画随机变量的稳定性呢?
课堂探究
问题2 怎样定量刻画离散型随机变量取值的离散程度
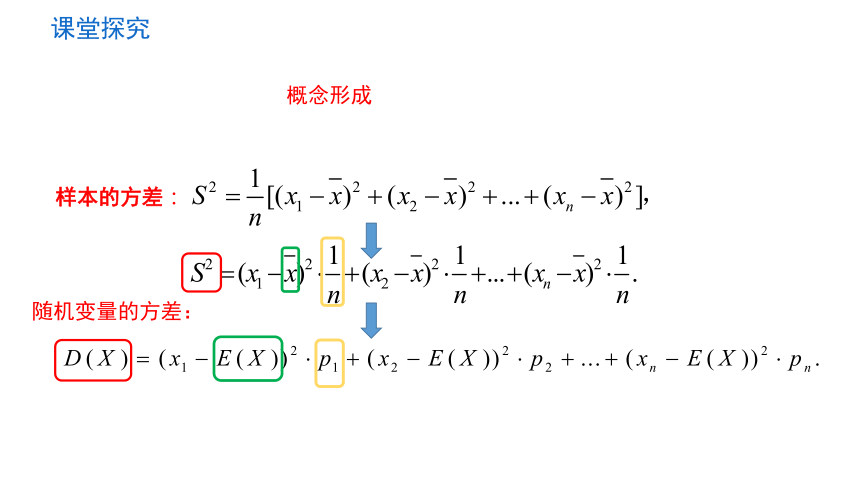
样本的方差:
随机变量的方差:
课堂探究
概念形成
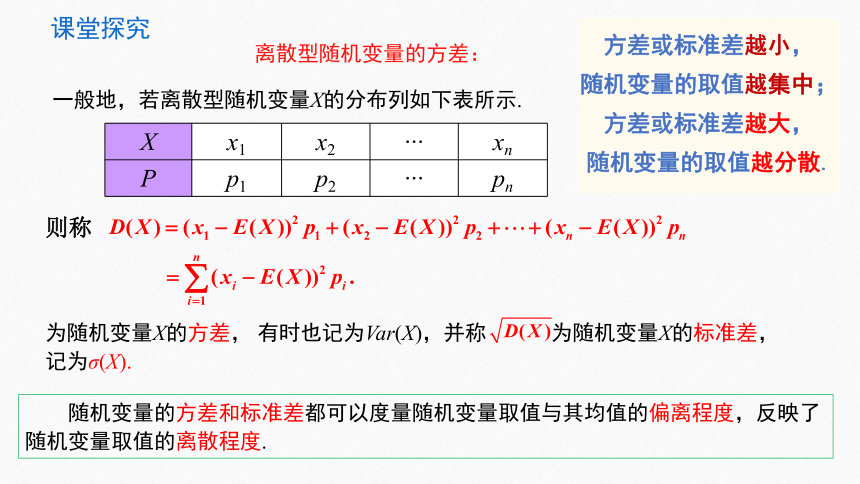
一般地,若离散型随机变量X的分布列如下表所示.
则称
为随机变量X的方差, 有时也记为Var(X),并称 为随机变量X的标准差,记为σ(X).
离散型随机变量的方差:
X x1 x2 xn
P p1 p2 pn
随机变量的方差和标准差都可以度量随机变量取值与其均值的偏离程度,反映了随机变量取值的离散程度.
方差或标准差越小,
随机变量的取值越集中;
方差或标准差越大,
随机变量的取值越分散.
课堂探究
证明:
课堂探究
问题3.方差的计算可以简化吗?
随机变量X,X+b,aX的分布列如下表:
...
...
...
...
课堂探究
问题4: 离散型随机变量X加上一个常数,方差会有怎样的变化 离散型随机变量X乘以一个常数,方差又有怎样的变化 它们和期望的性质有什么不同
所以
方差的性质:
1. 若X,Y 是两个随机变量, 且Y=aX+b, 则:D(Y )=D(aX+b)=a2D(X )
特殊地:
(1)当a=0时, D(b)=0.
(2)当b=0时,D(aX )=a2D(X ).
2. D(X )=E(X2)-E(X)2
课堂探究
X 1 2 3 4 5 6
P
课堂探究
例1 抛掷一枚质地均匀的骰子,求掷出的点数X的方差.
例1 抛掷一枚质地均匀的骰子,求掷出的点数X的方差.
解:随机变量X的分布列为
课堂探究
例题解析
方法规律
求离散型随机变量X 的方差、标准差的一般步骤:
①理解X 的意义,写出X 可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出 E(X );
④根据方差、标准差的定义求出D(X),σ(x)
课堂探究
解:
1. 已知随机变量X的分布列为
X 1 2 3 4
P 0.2 0.3 0.4 0.1
求D(X)和σ(2X+7).
课本练习P70
课堂探究
(或D(X)=E(X2)-(E(X))2=1×0.2+4×0.3+9×0.4+16×0.1-2.42=0.84).
σ(2X+7)=.
跟踪训练
例2 投资A,B两种股票,每股收益的分布列分别如下表所示.
股票A收益的分布列
股票B收益的分布列
收益X /元 -1 0 2
概率 0.1 0.3 0.6
收益Y /元 0 1 2
概率 0.3 0.4 0.3
投资哪种股票的期望收益大
(2) 投资哪种股票的风险较高
分析:股票投资收益是随机变量,期望收益就是随机变量的均值.投资风险是指收益的不确定性,在两种股票期望收益相差不大的情况下,可以用收益的方差来度量它们的投资风险高低,方差越大风险越高,方差越小风险越低
课堂探究
股票A收益的分布列
股票B收益的分布列
收益X /元 -1 0 2
概率 0.1 0.3 0.6
收益Y /元 0 1 2
概率 0.3 0.4 0.3
因为E(X)>E(Y), 所以投资股票A的期望收益较大.
解:(1)股票A和股票B投资收益的期望分别为
E(X)=(-1)×0.1+0×0.3+2×0.6=1.1,
E(Y)=0×0.3+1×0.4+2×0.3=1.
因为E(X)和E(Y)相差不大,且D(X)>D(Y), 所以投资股票A比投资股票B的风险高.
(2)股票A和股票B投资收益的方差分别为
D(X)=(-1)2×0.1+02×0.3+22×0.6 1.12=1.29,
D(Y)=02×0.3+12×0.4+22×0.3 12=0.6.
课堂探究
跟踪训练
2.有甲、乙两个单位都愿意聘用你,而你能获得如下信息:
甲单位不同职位月工资X1元 1200 1400 1600 1800
获得相应职位的概率P1 0.4 0.3 0.2 0.1
乙单位不同职位月工资X2元 1000 1400 1800 2200
获得相应职位的概率P2 0.4 0.3 0.2 0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
课堂探究
跟踪训练
甲单位不同职位月工资X1元 1200 1400 1600 1800
获得相应职位的概率P1 0.4 0.3 0.2 0.1
乙单位不同职位月工资X2元 1000 1400 1800 2200
获得相应职位的概率P2 0.4 0.3 0.2 0.1
解:E(X1)=12 00×0.4+1 400×0.3+1 600×0.2+1 800×0.1=1 400,
E(X2)=1 000×0.4+14 00×0.3+1 800×0.2+2 200×0.1=1 400,
D(X1)=40 000,D(X2)=160 000,
在两个单位工资的均值相等的情况下,如果认为自己能力很强,应选择工资方差大的单位,即乙单位;如果认为自己能力不强,就应选择工资方差小的单位,即甲单位.
课堂探究
1.已知随机变量X的分布列为P(X=k)= ,k=3,6,9,则D(X)=( )
A.6 B.9 C.3 D.4
A
2.若随机变量X服从两点分布,且在一次试验中事件A发生的概率P=0.5,则E(X)和D(X)分别为( )
A.0.25;0.5 B.0.5;0.75 C.0.5;0.25 D.1;0.75
C
3.已知随机变量X的方差为 ,则σ(X)=________.
评价反馈
评价反馈
4.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等,而两个野生动物保护区内每个季度发现违反保护条例的事件次数的分布列分别如下,
X 0 1 2 3
P 0.3 0.3 0.2 0.2
乙野生动物保护区:
Y 0 1 2
P 0.1 0.5 0.4
试评定这两个野生动物保护区的管理水平.
甲野生动物保护区
解: 甲野生动物保护区内违反保护条例的事件次数X的均值和方差为
E(X)=0×0.3+1×0.3+2×0.2+3×0.2=1.3,
D(X)=(0-1.3)2×0.3+(1-1.3)2×0.3+(2-1.3)2×0.2+(3-1.3)2×0.2=1.21.
乙野生动物保护区内违反保护条例的事件次数Y的均值和方差为
E(Y)=0×0.1+1×0.5+2×0.4=1.3,
D(Y)=(0-1.3)2×0.1+(1-1.3)2×0.5+(2-1.3)2×0.4=0.41.
因为E(X)=E(Y),D(X)>D(Y),所以两个野生动物保护区内每个季度发现违反保护条例的事件的平均次数相同,但甲野生动物保护区内的违规事件次数相对分散和波动,乙野生动物保护区内的违反保护条例的事件次数更加集中和稳定,所以乙野生动物野生动物保护区的管理水平比甲野生动物保护区高.
评价反馈
1.离散型随机变量X的方差、标准差
2.D(aX+b)=a2D(X)
3.求离散型随机变量X 的方差、标准差的一般步骤:
(1)理解X 的意义,写出X 可能取的全部值;
(2)求X取各个值的概率,写出分布列;
(3)根据分布列,由期望的定义求出 E(X );
(4)根据方差、标准差的定义求出D(X),σ(x)
课堂小结
谢谢大家
7.3.2 离散型随机变量的方差
第七章 随机变量及其分布
数学
学习目标
①通过具体实例,理解取有限值的离散型随机变量的方差、标准差的含义.
②能计算简单离散型随机变量的方差,并能解决一些实际问题.
③掌握方差的性质以及两点分布的方差的求法.
课堂导入
随机变量的均值是一个重要的数字特征,它反映了随机变量取值的平均水平或分布的“集中趋势”.
因为随机变量的取值围绕其均值波动,而随机变量的均值无法反映波动幅度的大小.
所以我们还需要寻找反映随机变量取值波动大小的数字特征.
问题1 从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列如下表所示.
如何评价这两名同学的射击水平
X 6 7 8 9 10
P 0.09 0.24 0.32 0.28 0.07
Y 6 7 8 9 10
P 0.07 0.22 0.38 0.30 0.03
通过计算可得
评价射击水平,除了要了解击中环数的均值外,还要考虑稳定性,即击中环数的离散程度.
E(X)= 8 ;E(Y)=8
由于E(X)=E(Y),所以根据均值不能区分这两名同学的射击水平.
课堂探究
作出甲、乙两名同学的概率分布图,如图:
比较两个图形,可以发现乙同学的射击成绩更集中于8环,即乙同学的射击成绩更稳定.而相对于乙同学,甲同学的成绩更加分散一些.
课堂探究
甲同学
乙同学
样本的离散程度是用哪个量刻画的?
样本方差
随机变量 X 的方差
能否用一个与样本方差类似的量来刻画随机变量的稳定性呢?
课堂探究
问题2 怎样定量刻画离散型随机变量取值的离散程度
样本的方差:
随机变量的方差:
课堂探究
概念形成
一般地,若离散型随机变量X的分布列如下表所示.
则称
为随机变量X的方差, 有时也记为Var(X),并称 为随机变量X的标准差,记为σ(X).
离散型随机变量的方差:
X x1 x2 xn
P p1 p2 pn
随机变量的方差和标准差都可以度量随机变量取值与其均值的偏离程度,反映了随机变量取值的离散程度.
方差或标准差越小,
随机变量的取值越集中;
方差或标准差越大,
随机变量的取值越分散.
课堂探究
证明:
课堂探究
问题3.方差的计算可以简化吗?
随机变量X,X+b,aX的分布列如下表:
...
...
...
...
课堂探究
问题4: 离散型随机变量X加上一个常数,方差会有怎样的变化 离散型随机变量X乘以一个常数,方差又有怎样的变化 它们和期望的性质有什么不同
所以
方差的性质:
1. 若X,Y 是两个随机变量, 且Y=aX+b, 则:D(Y )=D(aX+b)=a2D(X )
特殊地:
(1)当a=0时, D(b)=0.
(2)当b=0时,D(aX )=a2D(X ).
2. D(X )=E(X2)-E(X)2
课堂探究
X 1 2 3 4 5 6
P
课堂探究
例1 抛掷一枚质地均匀的骰子,求掷出的点数X的方差.
例1 抛掷一枚质地均匀的骰子,求掷出的点数X的方差.
解:随机变量X的分布列为
课堂探究
例题解析
方法规律
求离散型随机变量X 的方差、标准差的一般步骤:
①理解X 的意义,写出X 可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出 E(X );
④根据方差、标准差的定义求出D(X),σ(x)
课堂探究
解:
1. 已知随机变量X的分布列为
X 1 2 3 4
P 0.2 0.3 0.4 0.1
求D(X)和σ(2X+7).
课本练习P70
课堂探究
(或D(X)=E(X2)-(E(X))2=1×0.2+4×0.3+9×0.4+16×0.1-2.42=0.84).
σ(2X+7)=.
跟踪训练
例2 投资A,B两种股票,每股收益的分布列分别如下表所示.
股票A收益的分布列
股票B收益的分布列
收益X /元 -1 0 2
概率 0.1 0.3 0.6
收益Y /元 0 1 2
概率 0.3 0.4 0.3
投资哪种股票的期望收益大
(2) 投资哪种股票的风险较高
分析:股票投资收益是随机变量,期望收益就是随机变量的均值.投资风险是指收益的不确定性,在两种股票期望收益相差不大的情况下,可以用收益的方差来度量它们的投资风险高低,方差越大风险越高,方差越小风险越低
课堂探究
股票A收益的分布列
股票B收益的分布列
收益X /元 -1 0 2
概率 0.1 0.3 0.6
收益Y /元 0 1 2
概率 0.3 0.4 0.3
因为E(X)>E(Y), 所以投资股票A的期望收益较大.
解:(1)股票A和股票B投资收益的期望分别为
E(X)=(-1)×0.1+0×0.3+2×0.6=1.1,
E(Y)=0×0.3+1×0.4+2×0.3=1.
因为E(X)和E(Y)相差不大,且D(X)>D(Y), 所以投资股票A比投资股票B的风险高.
(2)股票A和股票B投资收益的方差分别为
D(X)=(-1)2×0.1+02×0.3+22×0.6 1.12=1.29,
D(Y)=02×0.3+12×0.4+22×0.3 12=0.6.
课堂探究
跟踪训练
2.有甲、乙两个单位都愿意聘用你,而你能获得如下信息:
甲单位不同职位月工资X1元 1200 1400 1600 1800
获得相应职位的概率P1 0.4 0.3 0.2 0.1
乙单位不同职位月工资X2元 1000 1400 1800 2200
获得相应职位的概率P2 0.4 0.3 0.2 0.1
根据工资待遇的差异情况,你愿意选择哪家单位?
课堂探究
跟踪训练
甲单位不同职位月工资X1元 1200 1400 1600 1800
获得相应职位的概率P1 0.4 0.3 0.2 0.1
乙单位不同职位月工资X2元 1000 1400 1800 2200
获得相应职位的概率P2 0.4 0.3 0.2 0.1
解:E(X1)=12 00×0.4+1 400×0.3+1 600×0.2+1 800×0.1=1 400,
E(X2)=1 000×0.4+14 00×0.3+1 800×0.2+2 200×0.1=1 400,
D(X1)=40 000,D(X2)=160 000,
在两个单位工资的均值相等的情况下,如果认为自己能力很强,应选择工资方差大的单位,即乙单位;如果认为自己能力不强,就应选择工资方差小的单位,即甲单位.
课堂探究
1.已知随机变量X的分布列为P(X=k)= ,k=3,6,9,则D(X)=( )
A.6 B.9 C.3 D.4
A
2.若随机变量X服从两点分布,且在一次试验中事件A发生的概率P=0.5,则E(X)和D(X)分别为( )
A.0.25;0.5 B.0.5;0.75 C.0.5;0.25 D.1;0.75
C
3.已知随机变量X的方差为 ,则σ(X)=________.
评价反馈
评价反馈
4.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等,而两个野生动物保护区内每个季度发现违反保护条例的事件次数的分布列分别如下,
X 0 1 2 3
P 0.3 0.3 0.2 0.2
乙野生动物保护区:
Y 0 1 2
P 0.1 0.5 0.4
试评定这两个野生动物保护区的管理水平.
甲野生动物保护区
解: 甲野生动物保护区内违反保护条例的事件次数X的均值和方差为
E(X)=0×0.3+1×0.3+2×0.2+3×0.2=1.3,
D(X)=(0-1.3)2×0.3+(1-1.3)2×0.3+(2-1.3)2×0.2+(3-1.3)2×0.2=1.21.
乙野生动物保护区内违反保护条例的事件次数Y的均值和方差为
E(Y)=0×0.1+1×0.5+2×0.4=1.3,
D(Y)=(0-1.3)2×0.1+(1-1.3)2×0.5+(2-1.3)2×0.4=0.41.
因为E(X)=E(Y),D(X)>D(Y),所以两个野生动物保护区内每个季度发现违反保护条例的事件的平均次数相同,但甲野生动物保护区内的违规事件次数相对分散和波动,乙野生动物保护区内的违反保护条例的事件次数更加集中和稳定,所以乙野生动物野生动物保护区的管理水平比甲野生动物保护区高.
评价反馈
1.离散型随机变量X的方差、标准差
2.D(aX+b)=a2D(X)
3.求离散型随机变量X 的方差、标准差的一般步骤:
(1)理解X 的意义,写出X 可能取的全部值;
(2)求X取各个值的概率,写出分布列;
(3)根据分布列,由期望的定义求出 E(X );
(4)根据方差、标准差的定义求出D(X),σ(x)
课堂小结
谢谢大家
