第七章 章末复习--人教A版高中数学选择性必修第三册教学课件(共27张PPT)
文档属性
| 名称 | 第七章 章末复习--人教A版高中数学选择性必修第三册教学课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 459.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:35:49 | ||
图片预览








文档简介
(共27张PPT)
章末复习
第七章 随机变量及其分布
数学
学习目标
①通过对所学随机变量及其分布知识进行总结和回顾,加深知识间的联系.
②通过各知识要点、典型例题的解法,对所学知识和方法进一步总结和提高.
学习重难点
重点:
离散型随机变量的分布列.
难点:
以二项分布、超几何分布、正态分布为模型的概率问题.
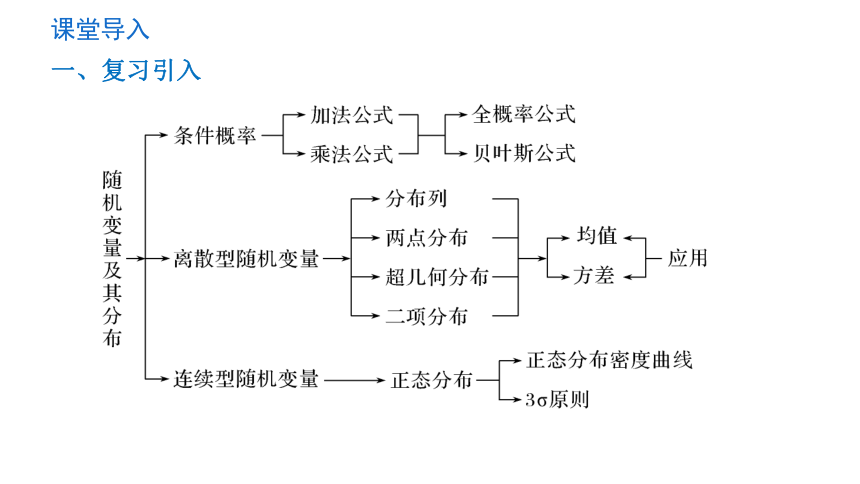
一、复习引入
课堂导入
要点一 条件概率的求法
例1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
(1)从5道题中不放回地依次抽取2道题包含的样本点数为
课堂探究
方法技巧
课堂探究
跟踪训练1
抛掷5枚硬币,在已知至少出现了2枚正面朝上的情况下,求:正面朝上数恰好是3枚的概率.
解法1:记“至少出现2枚正面朝上”为事件A,“恰好出现3枚正面朝上”为事件B,事件A包含的样本点的个数为n(A)= =26,事件B包含的样本点的个数为
解法2:
课堂探究
要点二 全概率公式
例2.设某批产品中, 甲、 乙、 丙三个工厂生产的产品分别占45%, 35%, 20%, 各厂的产品的次品率分别为4%, 2%, 5%, 现从中任取一件.
(1)求取到的是次品的概率;
(2)经检验发现取到的产品为次品, 求该产品是甲工厂生产的概率.
解:记事件A1=“该产品是甲工厂生产的”, 事件A2=“该产品为乙工厂生产的”,
事件A3=“该产品为丙工厂生产的”, 事件B=“该产品是次品”.
由题设,知P(A1)=45%,P(A2)=35%,P(A3)=20%,P(B|A1)=4%,P(B|A2)=2%,P(B|A3)=5%.
(1)由全概率公式得P(B)= P(Ai)P(B|Ai)=3.5%.
(2)由贝叶斯公式得
课堂探究
方法技巧
把事件B看作某一过程的结果,把Ai(i=1,2,…,n)看作该过程的若干个原因,每一原因发生的概率P(Ai)已知,且每一原因对结果的影响程度P(B|Ai)已知,如果已知事件B已经发生,要求此时是由第i个原因引起的概率,则用贝叶斯公式,即求P(Ai|B).贝叶斯公式反映了事件Ai发生的可能性在各种原因中的比重.
无论条件概率公式P(A|B)=,乘法公式P(AB)=P(B)P(A|B),还是贝叶斯公式 ,i=1,2,...,n,都反映了P(A),P(B|A),P(AB)三者之间的转化关系,灵活应用即可.
课堂探究
跟踪训练2
采购员要购买10个一包的电器元件.他的采购方法是:从一包中随机抽查3个,如果这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品.求:
(1)采购员拒绝购买的概率;
(2)在采购员拒绝购买的条件下,抽中的一包中含有4个次品的概率.
解:记事件B1={取到的是含4个次品的包 },事件B2={取到的是含1个次品的包 },事件A={采购员拒绝购买},则P(B1)=0.3,P(B2)=0.7,
(1)由全概率公式得
课堂探究
要点三 离散型随机变量的分布列、均值和方差
例3.已知随机变量X的分布列为下表,则 _____.
X 1 2 3
P 0.2 0.4 0.4
解:由题意知
则
课堂探究
21.2
方法技巧
求离散型随机变量X 的分布列、均值、方差、标准差的一般步骤:
①理解X 的意义,写出X 可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出 E(X );
④根据方差、标准差的定义求出D(X),σ(X)
课堂探究
跟踪训练3
袋中装有6个白球、2个黑球,从中任取3个球,则取到白球个数的期望 ( )
A.2 B. C. D.
答案:D
解析 : 取到的白球个数 可能的取值为1,2,3,
∴取到白球个数 的期望
课堂探究
D
要点四 n重伯努利试验、二项分布
例4.某公司招聘员工,先由两位专家面试,若这两位专家都同意通过,则通过初审并予以录用;若这两位专家都未同意通过,则未通过初审并不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为 ,获得复审专家通过的概率为 ,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率;
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
课堂探究
解: (1)设“某应聘人员被录用”为事件A,则
(2)根据题意,X~
故X的分布列为
X 0 1 2 3 4
P
课堂探究
方法技巧
(1) 若X~B(n,p),则P(X=k)= pk(1-p)n-k(k=0,1,2,…,n).
(2) 判断一个随机变量是否服从二项分布,关键有两点:
一是对立性,即一次试验中,事件发生与否两者必有其一;
二是重复性,即试验是独立重复地进行了n次.
课堂探究
跟踪训练4
某气象站天气预报的准确率为 ,计算(结果保留到小数点后面第2位)。
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.
解:令 X 表示5次预报中预报准确的次数,则
故其分布列为
(3)设5次预报中恰有2次准确,且其中第3次预报准确为事件为A,则
课堂探究
要点五 超几何分布
例5.在一次购物抽奖活动中,假设某10张奖券中有一等奖券1张,可获 得价值50元的奖品;有二等奖券3张,每张可获得价值10元的奖品;其余6张没有奖。某顾客从这10张中任抽2张。
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(单位:元)的分布列.
解:(1)记顾客中奖为事件A,则
(2)X所有可能的取值为(单位:元)0,10,20,50,60,
故X的分布列为
X 0 10 20 50 60
P
课堂探究
方法技巧
解决超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)在超几何分布中,只要知道M,N,n,就可以利用公式求出随机变量X取不同k值的概率P(X=k),从而求出X的分布列.
课堂探究
跟踪训练5
某学院为了调查本校学生2022年4月“健康上网”(健康上网是指每天上网不超过两个小时)的天数情况,随机抽取了40名本校学生,统计他们在该月30天内健康上网的天数,并将所得的数据分成以下六组:[0,5],(5,10],(10,15],…,(25,30],由此画出样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的分布列及均值E(Y).
课堂探究
解:(1)由题图可知健康上网天数未超过20天的频率为(0.01+0.02+0.03+0.09)×5=0.15×5=0.75,所以健康上网天数超过20天的学生人数是40×(1-0.75)=40×0.25=10.
课堂探究
要点六 正态分布
例6 .设X~N(10,1).
(1)证明:P(1(2)设P(X≤2)=a,求P(10(1)证明:因为X~N(10,1),所以正态曲线f(x)关于直线x=10对称,而区间(1,2)和(18,19)关于直线x=10对称,
故P(1课堂探究
例7.为了了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(单位:kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5 kg小于等于62.5 kg属于正常情况,则这1 000名男生中属于正常情况的人数是( )
A.997 B.954 C.819 D.683
答案:D
解析:由题意,可知μ=60.5,σ=2,故P(58.5从而属于正常情况的人数是1 000×68.3%=683.
课堂探究
D
方法技巧
正态分布的概率求法
(1)利用“3σ”原则,记住正态总体在三个区间内取值的概率.
(2)利用数形结合.由于正态分布密度曲线具有对称性,因此常结合图象,利用对称性,解决某一区间内的概率.
课堂探究
跟踪训练6
1.已知随机变量 ,若 ,则 _______.
2.某学校高三2 500名学生第二次模拟考试总成绩服从正态分布N(500,502),请你判断考生成绩X在550~600分的人数.
答案:0.2
解析:由正态分布的密度函数知,
解析:∵考生成绩X~N(500,502),∴μ=500,σ=50,
∴P(550<X≤600)= [P(500-2×50<X≤500+2×50)-P(500-50<X≤500+50)]
≈ ×(0.954 5-0.682 7)=0.135 9,
∴考生成绩在550~600分的人数为2 500×0.135 9≈340(人).
课堂探究
0.2
布置作业
梳理本章所学知识体系.
教材第90-91页复习参考题7第1-6题.
谢谢大家
章末复习
第七章 随机变量及其分布
数学
学习目标
①通过对所学随机变量及其分布知识进行总结和回顾,加深知识间的联系.
②通过各知识要点、典型例题的解法,对所学知识和方法进一步总结和提高.
学习重难点
重点:
离散型随机变量的分布列.
难点:
以二项分布、超几何分布、正态分布为模型的概率问题.
一、复习引入
课堂导入
要点一 条件概率的求法
例1.在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2道题,求:
(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
解:设“第1次抽到理科题”为事件A,“第2次抽到理科题”为事件B,则“第1次和第2次都抽到理科题”为事件AB.
(1)从5道题中不放回地依次抽取2道题包含的样本点数为
课堂探究
方法技巧
课堂探究
跟踪训练1
抛掷5枚硬币,在已知至少出现了2枚正面朝上的情况下,求:正面朝上数恰好是3枚的概率.
解法1:记“至少出现2枚正面朝上”为事件A,“恰好出现3枚正面朝上”为事件B,事件A包含的样本点的个数为n(A)= =26,事件B包含的样本点的个数为
解法2:
课堂探究
要点二 全概率公式
例2.设某批产品中, 甲、 乙、 丙三个工厂生产的产品分别占45%, 35%, 20%, 各厂的产品的次品率分别为4%, 2%, 5%, 现从中任取一件.
(1)求取到的是次品的概率;
(2)经检验发现取到的产品为次品, 求该产品是甲工厂生产的概率.
解:记事件A1=“该产品是甲工厂生产的”, 事件A2=“该产品为乙工厂生产的”,
事件A3=“该产品为丙工厂生产的”, 事件B=“该产品是次品”.
由题设,知P(A1)=45%,P(A2)=35%,P(A3)=20%,P(B|A1)=4%,P(B|A2)=2%,P(B|A3)=5%.
(1)由全概率公式得P(B)= P(Ai)P(B|Ai)=3.5%.
(2)由贝叶斯公式得
课堂探究
方法技巧
把事件B看作某一过程的结果,把Ai(i=1,2,…,n)看作该过程的若干个原因,每一原因发生的概率P(Ai)已知,且每一原因对结果的影响程度P(B|Ai)已知,如果已知事件B已经发生,要求此时是由第i个原因引起的概率,则用贝叶斯公式,即求P(Ai|B).贝叶斯公式反映了事件Ai发生的可能性在各种原因中的比重.
无论条件概率公式P(A|B)=,乘法公式P(AB)=P(B)P(A|B),还是贝叶斯公式 ,i=1,2,...,n,都反映了P(A),P(B|A),P(AB)三者之间的转化关系,灵活应用即可.
课堂探究
跟踪训练2
采购员要购买10个一包的电器元件.他的采购方法是:从一包中随机抽查3个,如果这3个元件都是好的,他才买下这一包.假定含有4个次品的包数占30%,而其余包中各含1个次品.求:
(1)采购员拒绝购买的概率;
(2)在采购员拒绝购买的条件下,抽中的一包中含有4个次品的概率.
解:记事件B1={取到的是含4个次品的包 },事件B2={取到的是含1个次品的包 },事件A={采购员拒绝购买},则P(B1)=0.3,P(B2)=0.7,
(1)由全概率公式得
课堂探究
要点三 离散型随机变量的分布列、均值和方差
例3.已知随机变量X的分布列为下表,则 _____.
X 1 2 3
P 0.2 0.4 0.4
解:由题意知
则
课堂探究
21.2
方法技巧
求离散型随机变量X 的分布列、均值、方差、标准差的一般步骤:
①理解X 的意义,写出X 可能取的全部值;
②求X取各个值的概率,写出分布列;
③根据分布列,由期望的定义求出 E(X );
④根据方差、标准差的定义求出D(X),σ(X)
课堂探究
跟踪训练3
袋中装有6个白球、2个黑球,从中任取3个球,则取到白球个数的期望 ( )
A.2 B. C. D.
答案:D
解析 : 取到的白球个数 可能的取值为1,2,3,
∴取到白球个数 的期望
课堂探究
D
要点四 n重伯努利试验、二项分布
例4.某公司招聘员工,先由两位专家面试,若这两位专家都同意通过,则通过初审并予以录用;若这两位专家都未同意通过,则未通过初审并不予录用;当这两位专家意见不一致时,再由第三位专家进行复审,若能通过复审则予以录用,否则不予录用.设应聘人员获得每位初审专家通过的概率均为 ,获得复审专家通过的概率为 ,各专家评审的结果相互独立.
(1)求某应聘人员被录用的概率;
(2)若4人应聘,设X为被录用的人数,试求随机变量X的分布列.
课堂探究
解: (1)设“某应聘人员被录用”为事件A,则
(2)根据题意,X~
故X的分布列为
X 0 1 2 3 4
P
课堂探究
方法技巧
(1) 若X~B(n,p),则P(X=k)= pk(1-p)n-k(k=0,1,2,…,n).
(2) 判断一个随机变量是否服从二项分布,关键有两点:
一是对立性,即一次试验中,事件发生与否两者必有其一;
二是重复性,即试验是独立重复地进行了n次.
课堂探究
跟踪训练4
某气象站天气预报的准确率为 ,计算(结果保留到小数点后面第2位)。
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第3次预报准确的概率.
解:令 X 表示5次预报中预报准确的次数,则
故其分布列为
(3)设5次预报中恰有2次准确,且其中第3次预报准确为事件为A,则
课堂探究
要点五 超几何分布
例5.在一次购物抽奖活动中,假设某10张奖券中有一等奖券1张,可获 得价值50元的奖品;有二等奖券3张,每张可获得价值10元的奖品;其余6张没有奖。某顾客从这10张中任抽2张。
(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(单位:元)的分布列.
解:(1)记顾客中奖为事件A,则
(2)X所有可能的取值为(单位:元)0,10,20,50,60,
故X的分布列为
X 0 10 20 50 60
P
课堂探究
方法技巧
解决超几何分布问题的两个关键点
(1)超几何分布是概率分布的一种形式,一定要注意公式中字母的范围及其意义,解决问题时可以直接利用公式求解,但不能机械地记忆.
(2)在超几何分布中,只要知道M,N,n,就可以利用公式求出随机变量X取不同k值的概率P(X=k),从而求出X的分布列.
课堂探究
跟踪训练5
某学院为了调查本校学生2022年4月“健康上网”(健康上网是指每天上网不超过两个小时)的天数情况,随机抽取了40名本校学生,统计他们在该月30天内健康上网的天数,并将所得的数据分成以下六组:[0,5],(5,10],(10,15],…,(25,30],由此画出样本的频率分布直方图,如图所示.
(1)根据频率分布直方图,求这40名学生中健康上网天数超过20天的人数;
(2)现从这40名学生中任取2名,设Y为取出的2名学生中健康上网天数超过20天的人数,求Y的分布列及均值E(Y).
课堂探究
解:(1)由题图可知健康上网天数未超过20天的频率为(0.01+0.02+0.03+0.09)×5=0.15×5=0.75,所以健康上网天数超过20天的学生人数是40×(1-0.75)=40×0.25=10.
课堂探究
要点六 正态分布
例6 .设X~N(10,1).
(1)证明:P(1
故P(1
例7.为了了解某地区高三男生的身体发育状况,抽查了该地区1 000名年龄在17.5岁至19岁的高三男生的体重情况,抽查结果表明他们的体重X(单位:kg)服从正态分布N(μ,22),且正态分布密度曲线如图所示.若体重大于58.5 kg小于等于62.5 kg属于正常情况,则这1 000名男生中属于正常情况的人数是( )
A.997 B.954 C.819 D.683
答案:D
解析:由题意,可知μ=60.5,σ=2,故P(58.5
课堂探究
D
方法技巧
正态分布的概率求法
(1)利用“3σ”原则,记住正态总体在三个区间内取值的概率.
(2)利用数形结合.由于正态分布密度曲线具有对称性,因此常结合图象,利用对称性,解决某一区间内的概率.
课堂探究
跟踪训练6
1.已知随机变量 ,若 ,则 _______.
2.某学校高三2 500名学生第二次模拟考试总成绩服从正态分布N(500,502),请你判断考生成绩X在550~600分的人数.
答案:0.2
解析:由正态分布的密度函数知,
解析:∵考生成绩X~N(500,502),∴μ=500,σ=50,
∴P(550<X≤600)= [P(500-2×50<X≤500+2×50)-P(500-50<X≤500+50)]
≈ ×(0.954 5-0.682 7)=0.135 9,
∴考生成绩在550~600分的人数为2 500×0.135 9≈340(人).
课堂探究
0.2
布置作业
梳理本章所学知识体系.
教材第90-91页复习参考题7第1-6题.
谢谢大家
