第八章 8.6.2直线与平面垂直--人教A版高中数学必修第二册教学课件(共38张PPT)
文档属性
| 名称 | 第八章 8.6.2直线与平面垂直--人教A版高中数学必修第二册教学课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 899.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:39:57 | ||
图片预览











文档简介
(共38张PPT)
8.6.2直线与平面垂直
第八章 立体几何初步
数学
一、学习目标
二、课堂探究
三、课堂练习
四、课堂小结
五、课后作业
一、学习目标
(1)理解并掌握直线与平面所成角的定义,直线与平面垂直的定义;
(2)掌握空间中点到平面的距离、直线到平面的距离,平行平面间的距离;
(3)探究并掌握直线与平面的判定定理与性质定理.
【导入新课】在日常生活中,我们对直线与平面垂直有很多感性认识. 比如,旗杆与地面的位置关系,教室里相邻墙面的交线与地面的位置关系等,都给我们以直线与平面垂直的形象.
【问题探究1】如图,在阳光下观察直立于地面的旗杆AB及它在地面的影子BC. 随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直
二、课堂探究
结论:事实上,随着时间的变化,尽管影子BC的位置在不断地变化,但是旗杆AB所在直线始终与影子BC所在直线垂直. 也就是说,旗杆AB所在直线与地面上任意一条过点B的直线垂直. 对于地面上不过点B的任意一条直线B'C',总能在地面上找到过点B的一条直线与之平行,根据异面直线垂直的定义,可知旗杆AB所在直线与直线B'C'也垂直. 因此,旗杆AB所在直线与地面上任意一条直线都垂直.
二、课堂探究
由此,我们得到直线与平面垂直的定义:
一般地,如果直线 l 与平面 α 内的任意一条直线都垂直,我们就说直线 l 与平面 α 互相垂直,记作 l ⊥ α .直线 l 叫做平面 α 的垂线,平面 α 叫做直线 l 的垂面. 直线与平面垂直时,它们唯一的公共点P 叫做垂足.
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示:
二、课堂探究
思考1:在同一平面内,过一点有且只有一条直线与已知直线垂直. 将这一结论推广到空间,过一点垂直于已知平面的直线有几条?为什么?
结论:过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
二、课堂探究
二、课堂探究
【问题探究2】如图,准备一块三角形纸片ABC,过△ABC 的顶点A 翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触).
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面垂直?为什么?
二、课堂探究
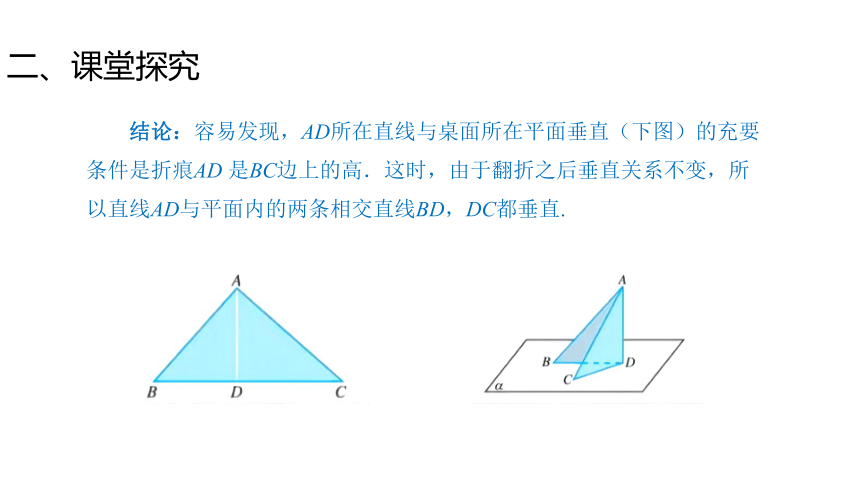
结论:容易发现,AD所在直线与桌面所在平面垂直(下图)的充要条件是折痕AD 是BC边上的高.这时,由于翻折之后垂直关系不变,所以直线AD与平面内的两条相交直线BD,DC都垂直.
事实上,由基本事实的推论2,平面可以看成是由两条相交直线BD,DC所唯一确定的,所以当直线AD垂直于这两条相交直线时,就能保证直线AD与内所有直线都垂直.
由以上探究,我们有如下判定直线与平面垂直的定理:
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
二、课堂探究
【思考2】两条相交直线可以确定一个平面. 两条平行直线也可以确定一个平面,那么定理中的“两条相交直线”可以改为“两条平行直线”吗?你能从向量的角度解释原因吗?如果改为“无数条直线”呢?
结论:不可以,与两条相交直线共线的向量可以表示两者确定的平面内的所有向量,因此可以证明已知直线与该平面内所有直线垂直,由直线与平面垂直的定义,可知已知直线与已知平面垂直,但是两条平行直线达不到上述效果,因此不可以;改成无数条直线也不可以,比如这无数条直线平行时.
二、课堂探究
【思考3】结合异面直线之间的位置关系,直线与平面相交时,除了直线与平面垂直这一关系外,其他情况下应该如何描述直线与平面的位置关系?
结论:如图所示,一条直线 l 与一个平面 α 相交,但不与这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足.过斜线上斜足以外的一点P向平面 α 引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影. 平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
二、课堂探究
一条直线垂直于平面,我们说它们所成的角是90°;一条直线和平面平行,或在平面内,我们说它们所成的角是0°. 直线与平面所成的角θ的取值范围是0° ≤ θ ≤ 90°.
二、课堂探究
【问题探究3】
(1)如图①,在长方体ABCD-A'B'C'D'中,棱AA',BB',CC',DD'所在直线都垂直于平面ABCD,它们之间具有什么位置关系
(2)如图②,已知直线a,b和平面α. 如果a⊥α,b⊥α,那么直线a,b一定平行吗
由(1)(2),我们能否得到什么结论?能否给出证明?
① ②
二、课堂探究
结论:可以发现,这些直线相互平行. 不失一般性,我们以(2)为例加以证明.
(反证法)如图,假设 b 与 a 不平行,且b ∩ a =O.显然点O不在直线 a 上,所以点O与直线 a 可确定一个平面,在该平面内过点O作直线 b'// a ,则直线 b 与 b'是相交于点O的两条不同直线,所以直线 b 与 b' 可确定平面 β,设α ∩ β= c,则O∈ c.因为 a ⊥α , b⊥α ,所以 a ⊥ c, b⊥ c.又因为 b'// a ,所以 b'⊥ c. 这样在平面 β内,经过直线 c上同一点O就有两条直线 b , b'与 c 垂直,显然不可能. 因此 b // a .
二、课堂探究
这样,我们得到了直线与平面垂直的性质定理:
垂直于同一个平面的两条直线平行.
二、课堂探究
【问题探究4】
直线 l 平行于平面 α,那么直线 l 上各点到平面 α 的距离是否相等?请证明你的结论.
结论:直线l上各点到平面α的距离相等.
二、课堂探究
【问题探究4】
证明:过直线 l 上任意两点A,B分别作平面 α 的垂线AA1,BB1,垂足分别为A1,B1.
∵AA1⊥α,BB1⊥α,∴AA1//BB1.
设直线AA1,BB1确定的平面为β,β∩α= A1B1.
∴l //α,∴ l //A1B1.
. 四边形AA1B1B是矩形.
∴AA1= BB1.
由A,B是直线 l 上任取的两点,可知直线 l 上各点到平面 α 的距离相等.
二、课堂探究
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离. 由上面探究我们还可以进一步得出,如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
二、课堂探究
【小试牛刀】
例1 求证:如果两条平行直线中的一条直线垂直于一个平面, 那么另一条直线也垂直于这个平面.
二、课堂探究
已知:a∥b,a⊥α,求证b⊥α
【小试牛刀】
二、课堂探究
已知:如图,a∥b,a⊥α,求证:b⊥α.
证明 如图,在平面α内取两条相交直线m,n.
因为直线a⊥α,
所以a⊥m,a⊥n.
因为a∥b,所以b⊥m,b⊥n.
又m α,n α,m,n是两条相交直线,
所以b⊥α.
【跟踪训练】
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
(1)求证:DE //平面ABC;(2)求证:B1C⊥平面BDE.
证明:(1)设G是CC1的中点,连接EG,DG,
∵E为B1C的中点,∴EG //B1C1,
而BC//B1C1,∴EG // BC,
∵EG 平面ABC,BC 平面ABC,∴EG //平面ABC,
同理可证DG//平面ABC,因为EG,DG 平面DEG,且EG∩DG = G,
∴平面DEG // 平面ABC,而DE 平面DEG ,所以DE //平面ABC;
二、课堂探究
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
(1)求证:DE //平面ABC;(2)求证:B1C⊥平面BDE.
(2)设O是BC的中点,连接AO,EO,
∵E为B1C的中点,∴EO //B1B,而AD //B1B,∴EO //AD,
由(1)可知:平面DEG //平面ABC,
平面AOED∩平面DEG = DE,平面AOED∩平面ABC = AO,
∴OA // DE,
在正三棱柱ABC-A1B1C1中,平面BCC1B1⊥平面ABC,而平面BCC1B1∩平面ABC = BC,
∵ΔABC是正三角形,O是BC的中点,∴AO⊥BC,
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
(1)求证:DE //平面ABC;(2)求证:B1C⊥平面BDE.
∴AO⊥平面BCC1B1,
而CB1 平面BCC1B1,∴AO⊥CB1,
而OA // DE,∴ DE⊥CB1,
∵正三棱柱ABC-A1B1C1中棱长都相等,
∴BB1 = BC,而E分别为B1C的中点,
∴ BE⊥CB1,而BE,DE 平面BDE,BE∩DE = E,
∴B1C⊥平面BDE.
【名师解惑】
证明直线与平面垂直的常用方法:
(1)线面垂直的定义;
(2)线面垂直的判定定理;
(3)如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
二、课堂探究
【小试牛刀】
例2 如图, 在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1DCB1所成的角.
二、课堂探究
解:如图,连接BC1,BC1与B1C相交于点O,连接A1O,设正方体的棱长为a
∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1.
∴A1B1⊥BC1.
又BC1⊥B1C,
∴BC1⊥平面A1DCB1.
【小试牛刀】
例2 如图, 在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1DCB1所成的角.
所以∠BA1O为直线A1B和平面A1DCB1所成的角.
在Rt△A1BO中,A1B=a,BO=a,
∴BO= A1B
∴∠BA1O=30°.
∴直线A1B和平面A1DCB1所成的角为30°.
二、课堂探究
【跟踪训练】
如图,在四棱锥P-ABCD中,AD⊥CD,AD∥BC,AD = 2BC = 2CD = 4,PC = ,ΔPAD是正三角形.
(1)求证:CD⊥PA;
(2)求AB与平面PCD所成角的余弦值.
二、课堂探究
【跟踪训练】
二、课堂探究
(1)证明 ∵△PAD是正三角形,AD=2CD=4,
∴PD=4,CD=2.
又PC=
∴PC2=PD2+CD2.∴CD⊥PD.
又AD⊥CD,AD∩PD=D,
∴CD⊥平面PAD.
∵PA 平面PAD,
∴CD⊥PA.
如图,取PD的中点E,连接AE,延长DC,AB交于点H,连接EH,
∵△PAD是正三角形,
∴AE⊥PD,AE=
由(1)得CD⊥平面PAD,
∴CD⊥AE.
∵CD∩PD=D,CD,PD 平面PCD,
∴AE⊥平面PCD.
∴∠AHE就是AB与平面PCD所成的角,
∵AD⊥CD,BC∥AD,AD=2BC=2CD=4,
【跟踪训练】
二、课堂探究
∴DH=4,AH=4 ,EH= =2
∴cos∠AHE== = =
∴AB与平面PCD所成角的余弦值为
【跟踪训练】
二、课堂探究
求斜线与平面所成角的步骤:
(1)作:作出斜线在平面内的射影,方法是过斜线上异于斜足的一点作平面的垂线,斜足与垂足所确定的直线就是斜线在平面内的射影;注意斜线上点的选取尽可能利用已知信息,尽量简化计算.
(2)证:若题目已知中已存在射影,则只需证明即可.
(3)算:在垂线段、斜线和射影所组成的直角三角形中计算出斜线与其射影所成的角,即斜线与平面所成的角.
【跟踪训练】
二、课堂探究
三、课堂练习
A
1.如图,在正方形ABCD中,E,F分别为BC,CD的中点,H是EF的中点.若沿AE,AF,EF把这个正方形折成一个几何体,使B,C,D三点重合于点G,则下列结论中成立的是( )
A.AG⊥平面EFG B.AH⊥平面EFG
C.GF⊥平面AEF D.GH⊥平面AEF
2. 如图,四棱锥S-ABCD的底面为正方形, SD⊥底面ABCD,则下列结论中不正确的是( )
A. AC⊥SB
B. 三棱锥S-BCD的四个面中有3个直角三角形
C. SA与平面SBD所成的角等于SC与平面SBD所成的角
D. AB与SC所成的角等于DC与SA所成的角
BD
三、课堂练习
3. 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于点E,AF⊥PC于点F.
(1)求证:PC⊥平面AEF;
(2)设平面AEF交PD于点G,求证:AG⊥PD.
三、课堂练习
四、课堂小结
(1)线面垂直的概念;
(2)线面垂直的判定定理与性质定理;
(3)直线与平面的夹角的概念及其求法;
(4)直线与平面垂直的判定定理与性质定理的应用.
五、课后作业
必做题:完成学案后的课后巩固.
选做题:完成学案后的核心素养专练
谢谢大家
8.6.2直线与平面垂直
第八章 立体几何初步
数学
一、学习目标
二、课堂探究
三、课堂练习
四、课堂小结
五、课后作业
一、学习目标
(1)理解并掌握直线与平面所成角的定义,直线与平面垂直的定义;
(2)掌握空间中点到平面的距离、直线到平面的距离,平行平面间的距离;
(3)探究并掌握直线与平面的判定定理与性质定理.
【导入新课】在日常生活中,我们对直线与平面垂直有很多感性认识. 比如,旗杆与地面的位置关系,教室里相邻墙面的交线与地面的位置关系等,都给我们以直线与平面垂直的形象.
【问题探究1】如图,在阳光下观察直立于地面的旗杆AB及它在地面的影子BC. 随着时间的变化,影子BC的位置在不断地变化,旗杆所在直线AB与其影子BC所在直线是否保持垂直
二、课堂探究
结论:事实上,随着时间的变化,尽管影子BC的位置在不断地变化,但是旗杆AB所在直线始终与影子BC所在直线垂直. 也就是说,旗杆AB所在直线与地面上任意一条过点B的直线垂直. 对于地面上不过点B的任意一条直线B'C',总能在地面上找到过点B的一条直线与之平行,根据异面直线垂直的定义,可知旗杆AB所在直线与直线B'C'也垂直. 因此,旗杆AB所在直线与地面上任意一条直线都垂直.
二、课堂探究
由此,我们得到直线与平面垂直的定义:
一般地,如果直线 l 与平面 α 内的任意一条直线都垂直,我们就说直线 l 与平面 α 互相垂直,记作 l ⊥ α .直线 l 叫做平面 α 的垂线,平面 α 叫做直线 l 的垂面. 直线与平面垂直时,它们唯一的公共点P 叫做垂足.
画直线与平面垂直时,通常把直线画成与表示平面的平行四边形的一边垂直,如图所示:
二、课堂探究
思考1:在同一平面内,过一点有且只有一条直线与已知直线垂直. 将这一结论推广到空间,过一点垂直于已知平面的直线有几条?为什么?
结论:过一点垂直于已知平面的直线有且只有一条.
过一点作垂直于已知平面的直线,则该点与垂足间的线段,叫做这个点到该平面的垂线段,垂线段的长度叫做这个点到该平面的距离.
二、课堂探究
二、课堂探究
【问题探究2】如图,准备一块三角形纸片ABC,过△ABC 的顶点A 翻折纸片,得到折痕AD,将翻折后的纸片竖起放置在桌面上(BD,DC与桌面接触).
(1)折痕AD与桌面垂直吗?
(2)如何翻折才能使折痕AD与桌面垂直?为什么?
二、课堂探究
结论:容易发现,AD所在直线与桌面所在平面垂直(下图)的充要条件是折痕AD 是BC边上的高.这时,由于翻折之后垂直关系不变,所以直线AD与平面内的两条相交直线BD,DC都垂直.
事实上,由基本事实的推论2,平面可以看成是由两条相交直线BD,DC所唯一确定的,所以当直线AD垂直于这两条相交直线时,就能保证直线AD与内所有直线都垂直.
由以上探究,我们有如下判定直线与平面垂直的定理:
如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.
二、课堂探究
【思考2】两条相交直线可以确定一个平面. 两条平行直线也可以确定一个平面,那么定理中的“两条相交直线”可以改为“两条平行直线”吗?你能从向量的角度解释原因吗?如果改为“无数条直线”呢?
结论:不可以,与两条相交直线共线的向量可以表示两者确定的平面内的所有向量,因此可以证明已知直线与该平面内所有直线垂直,由直线与平面垂直的定义,可知已知直线与已知平面垂直,但是两条平行直线达不到上述效果,因此不可以;改成无数条直线也不可以,比如这无数条直线平行时.
二、课堂探究
【思考3】结合异面直线之间的位置关系,直线与平面相交时,除了直线与平面垂直这一关系外,其他情况下应该如何描述直线与平面的位置关系?
结论:如图所示,一条直线 l 与一个平面 α 相交,但不与这个平面垂直,这条直线叫做这个平面的斜线,斜线和平面的交点A叫做斜足.过斜线上斜足以外的一点P向平面 α 引垂线PO,过垂足O和斜足A的直线AO叫做斜线在这个平面上的射影. 平面的一条斜线和它在平面上的射影所成的角,叫做这条直线和这个平面所成的角.
二、课堂探究
一条直线垂直于平面,我们说它们所成的角是90°;一条直线和平面平行,或在平面内,我们说它们所成的角是0°. 直线与平面所成的角θ的取值范围是0° ≤ θ ≤ 90°.
二、课堂探究
【问题探究3】
(1)如图①,在长方体ABCD-A'B'C'D'中,棱AA',BB',CC',DD'所在直线都垂直于平面ABCD,它们之间具有什么位置关系
(2)如图②,已知直线a,b和平面α. 如果a⊥α,b⊥α,那么直线a,b一定平行吗
由(1)(2),我们能否得到什么结论?能否给出证明?
① ②
二、课堂探究
结论:可以发现,这些直线相互平行. 不失一般性,我们以(2)为例加以证明.
(反证法)如图,假设 b 与 a 不平行,且b ∩ a =O.显然点O不在直线 a 上,所以点O与直线 a 可确定一个平面,在该平面内过点O作直线 b'// a ,则直线 b 与 b'是相交于点O的两条不同直线,所以直线 b 与 b' 可确定平面 β,设α ∩ β= c,则O∈ c.因为 a ⊥α , b⊥α ,所以 a ⊥ c, b⊥ c.又因为 b'// a ,所以 b'⊥ c. 这样在平面 β内,经过直线 c上同一点O就有两条直线 b , b'与 c 垂直,显然不可能. 因此 b // a .
二、课堂探究
这样,我们得到了直线与平面垂直的性质定理:
垂直于同一个平面的两条直线平行.
二、课堂探究
【问题探究4】
直线 l 平行于平面 α,那么直线 l 上各点到平面 α 的距离是否相等?请证明你的结论.
结论:直线l上各点到平面α的距离相等.
二、课堂探究
【问题探究4】
证明:过直线 l 上任意两点A,B分别作平面 α 的垂线AA1,BB1,垂足分别为A1,B1.
∵AA1⊥α,BB1⊥α,∴AA1//BB1.
设直线AA1,BB1确定的平面为β,β∩α= A1B1.
∴l //α,∴ l //A1B1.
. 四边形AA1B1B是矩形.
∴AA1= BB1.
由A,B是直线 l 上任取的两点,可知直线 l 上各点到平面 α 的距离相等.
二、课堂探究
一条直线与一个平面平行时,这条直线上任意一点到这个平面的距离,叫做这条直线到这个平面的距离. 由上面探究我们还可以进一步得出,如果两个平面平行,那么其中一个平面内的任意一点到另一个平面的距离都相等,我们把它叫做这两个平行平面间的距离.
二、课堂探究
【小试牛刀】
例1 求证:如果两条平行直线中的一条直线垂直于一个平面, 那么另一条直线也垂直于这个平面.
二、课堂探究
已知:a∥b,a⊥α,求证b⊥α
【小试牛刀】
二、课堂探究
已知:如图,a∥b,a⊥α,求证:b⊥α.
证明 如图,在平面α内取两条相交直线m,n.
因为直线a⊥α,
所以a⊥m,a⊥n.
因为a∥b,所以b⊥m,b⊥n.
又m α,n α,m,n是两条相交直线,
所以b⊥α.
【跟踪训练】
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
(1)求证:DE //平面ABC;(2)求证:B1C⊥平面BDE.
证明:(1)设G是CC1的中点,连接EG,DG,
∵E为B1C的中点,∴EG //B1C1,
而BC//B1C1,∴EG // BC,
∵EG 平面ABC,BC 平面ABC,∴EG //平面ABC,
同理可证DG//平面ABC,因为EG,DG 平面DEG,且EG∩DG = G,
∴平面DEG // 平面ABC,而DE 平面DEG ,所以DE //平面ABC;
二、课堂探究
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
(1)求证:DE //平面ABC;(2)求证:B1C⊥平面BDE.
(2)设O是BC的中点,连接AO,EO,
∵E为B1C的中点,∴EO //B1B,而AD //B1B,∴EO //AD,
由(1)可知:平面DEG //平面ABC,
平面AOED∩平面DEG = DE,平面AOED∩平面ABC = AO,
∴OA // DE,
在正三棱柱ABC-A1B1C1中,平面BCC1B1⊥平面ABC,而平面BCC1B1∩平面ABC = BC,
∵ΔABC是正三角形,O是BC的中点,∴AO⊥BC,
如图,在棱长都相等的正三棱柱ABC-A1B1C1中,D,E分别为AA1,B1C的中点.
(1)求证:DE //平面ABC;(2)求证:B1C⊥平面BDE.
∴AO⊥平面BCC1B1,
而CB1 平面BCC1B1,∴AO⊥CB1,
而OA // DE,∴ DE⊥CB1,
∵正三棱柱ABC-A1B1C1中棱长都相等,
∴BB1 = BC,而E分别为B1C的中点,
∴ BE⊥CB1,而BE,DE 平面BDE,BE∩DE = E,
∴B1C⊥平面BDE.
【名师解惑】
证明直线与平面垂直的常用方法:
(1)线面垂直的定义;
(2)线面垂直的判定定理;
(3)如果两条平行直线的一条直线垂直于一个平面,那么另一条直线也垂直于这个平面.
二、课堂探究
【小试牛刀】
例2 如图, 在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1DCB1所成的角.
二、课堂探究
解:如图,连接BC1,BC1与B1C相交于点O,连接A1O,设正方体的棱长为a
∵A1B1⊥B1C1,A1B1⊥B1B,B1C1∩B1B=B1,
∴A1B1⊥平面BCC1B1.
∴A1B1⊥BC1.
又BC1⊥B1C,
∴BC1⊥平面A1DCB1.
【小试牛刀】
例2 如图, 在正方体ABCD-A1B1C1D1中,求直线A1B和平面A1DCB1所成的角.
所以∠BA1O为直线A1B和平面A1DCB1所成的角.
在Rt△A1BO中,A1B=a,BO=a,
∴BO= A1B
∴∠BA1O=30°.
∴直线A1B和平面A1DCB1所成的角为30°.
二、课堂探究
【跟踪训练】
如图,在四棱锥P-ABCD中,AD⊥CD,AD∥BC,AD = 2BC = 2CD = 4,PC = ,ΔPAD是正三角形.
(1)求证:CD⊥PA;
(2)求AB与平面PCD所成角的余弦值.
二、课堂探究
【跟踪训练】
二、课堂探究
(1)证明 ∵△PAD是正三角形,AD=2CD=4,
∴PD=4,CD=2.
又PC=
∴PC2=PD2+CD2.∴CD⊥PD.
又AD⊥CD,AD∩PD=D,
∴CD⊥平面PAD.
∵PA 平面PAD,
∴CD⊥PA.
如图,取PD的中点E,连接AE,延长DC,AB交于点H,连接EH,
∵△PAD是正三角形,
∴AE⊥PD,AE=
由(1)得CD⊥平面PAD,
∴CD⊥AE.
∵CD∩PD=D,CD,PD 平面PCD,
∴AE⊥平面PCD.
∴∠AHE就是AB与平面PCD所成的角,
∵AD⊥CD,BC∥AD,AD=2BC=2CD=4,
【跟踪训练】
二、课堂探究
∴DH=4,AH=4 ,EH= =2
∴cos∠AHE== = =
∴AB与平面PCD所成角的余弦值为
【跟踪训练】
二、课堂探究
求斜线与平面所成角的步骤:
(1)作:作出斜线在平面内的射影,方法是过斜线上异于斜足的一点作平面的垂线,斜足与垂足所确定的直线就是斜线在平面内的射影;注意斜线上点的选取尽可能利用已知信息,尽量简化计算.
(2)证:若题目已知中已存在射影,则只需证明即可.
(3)算:在垂线段、斜线和射影所组成的直角三角形中计算出斜线与其射影所成的角,即斜线与平面所成的角.
【跟踪训练】
二、课堂探究
三、课堂练习
A
1.如图,在正方形ABCD中,E,F分别为BC,CD的中点,H是EF的中点.若沿AE,AF,EF把这个正方形折成一个几何体,使B,C,D三点重合于点G,则下列结论中成立的是( )
A.AG⊥平面EFG B.AH⊥平面EFG
C.GF⊥平面AEF D.GH⊥平面AEF
2. 如图,四棱锥S-ABCD的底面为正方形, SD⊥底面ABCD,则下列结论中不正确的是( )
A. AC⊥SB
B. 三棱锥S-BCD的四个面中有3个直角三角形
C. SA与平面SBD所成的角等于SC与平面SBD所成的角
D. AB与SC所成的角等于DC与SA所成的角
BD
三、课堂练习
3. 如图,PA⊥平面ABCD,底面ABCD为矩形,AE⊥PB于点E,AF⊥PC于点F.
(1)求证:PC⊥平面AEF;
(2)设平面AEF交PD于点G,求证:AG⊥PD.
三、课堂练习
四、课堂小结
(1)线面垂直的概念;
(2)线面垂直的判定定理与性质定理;
(3)直线与平面的夹角的概念及其求法;
(4)直线与平面垂直的判定定理与性质定理的应用.
五、课后作业
必做题:完成学案后的课后巩固.
选做题:完成学案后的核心素养专练
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
