第八章 本章小结--人教A版高中数学必修第二册教学课件(共36张PPT)
文档属性
| 名称 | 第八章 本章小结--人教A版高中数学必修第二册教学课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:40:24 | ||
图片预览










文档简介
(共36张PPT)
第八章末小结
第1课时
第八章 空间点、直线、平面之间的位置关系
数学
学习目标
①在回顾与思考本章的主要内容的基础上,引导学生梳理立体几何的核心概念、定理等内容与思想方法,构建立体几何的核心体系,体会研究空间图形的基本思路:直观感知、操作确认、推理论证、度量计算.
②借助分析典型问题的通性通法,通过“图”(识图、画图、用图)提升学生直观想象素养,通过“写”(图形、文字、符号三种语言)培养学生逻辑推理能力,通过“悟”(直观感知、操作确认)发展学生数学抽象水平.
学习重难点
重点:
通过分析常见几何图形及典型问题,梳理立体几何初步的核心概念、定理等内容与思想方法,从而构建立体几何的核心体系.
难点:
分析组合体的结构特征以及运用有关定理推理证明一些几何元素间的位置关系.
导入新课
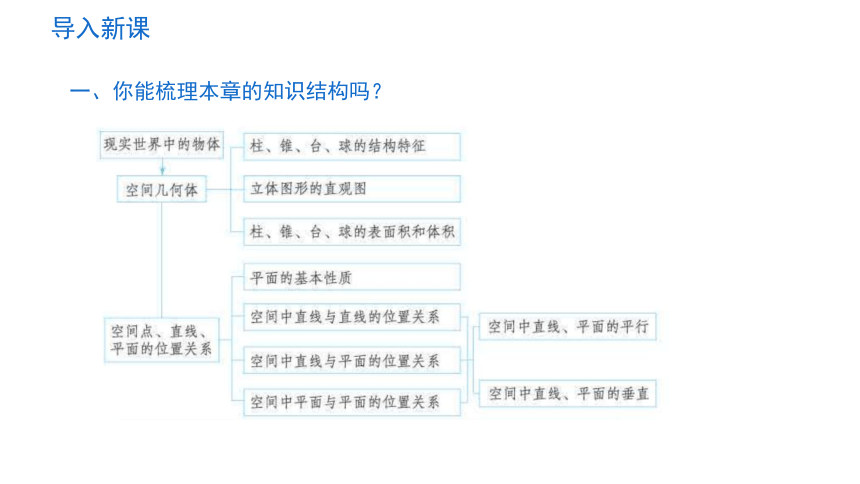
一、你能梳理本章的知识结构吗?
导入新课
二、核心知识归纳:问题与思考
问题1:我们是从哪些角度入手研究基本几何体的结构特征的 你能用基本几何体的结构特征解释身边物体的结构吗 请举例说明.
答案:我们从对空间几何体(实物、模型、图片等)的整体观察入手,认识多面体、旋转体以及一些基本几何体(棱柱、棱锥、棱台、圆柱、圆锥、圆台、球)的结构特征,研究这些几何体的组成元素及其相互关系.
导入新课
二、核心知识归纳:问题与思考
问题1:我们是从哪些角度入手研究基本几何体的结构特征的 你能用基本几何体的结构特征解释身边物体的结构吗 请举例说明.
答案:我们从对空间几何体(实物、模型、图片等)的整体观察入手,认识多面体、旋转体以及一些基本几何体(棱柱、棱锥、棱台、圆柱、圆锥、圆台、球)的结构特征,研究这些几何体的组成元素及其相互关系.
讲授新课
例1(1)(2020课标Ⅰ.理)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B.
C. D.
C
答案:C.
解析:如图,设,则,
由题意,即,化简得,
解得(负值舍去).故选C.
讲授新课
(2)将长与宽分别为6和4的矩形卷成一个圆柱(无重叠部分),则该圆柱的底面半径为________.
或
解析:(1)若以6为底面圆周长,则,;
(2)若以4为底面圆周长,则,
讲授新课
问题2:利用斜二测画法可以画出空间几何体的直观图,你能结合实例说出用斜二测画法画空间几何体的直观图的基本步吗
答案:斜二测画法画空间几何体的直观图,是用平面图形表示空间图形的重要方法,我们能够根据直观图想象空间几何体的形状和结构.简单说,斜二测画法的规则是:横竖不变,纵减半,平行性不变.
OC=2O'C'=2,
讲授新课
例2(2024·浙江G5联盟高一期中联考)已知水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',已知A'B'=2,B'C'=1,则四边形ABCD的面积为( )
A.2 B.4
C.6 D.8
C
答案:B
解析: 因为A'B'=2,B'C'=1,取A'B'的中点O'为坐标原点,以O'C'为y'轴建立坐标系O'x'y'如左图.
因为斜二测直观图为矩形A'B'C'D',A'O'=O'B'=1,B'C'=1,
则O'C',
可得原图ABCD(右图)中,AB=A'B'=2,
所以四边形的面积为AB·OC=2×24.
故选B.
讲授新课
名师解惑
名师解惑:利用斜二测画法画空间几何体的直观图的注意点
(1)画空间几何体的直观图在要求不太严格的情况下,长度和角度可适当选取.为了增强立体感,被挡住的部分通常用虚线表示.
(2)画法规则可简记为:两轴夹角为45°,竖轴垂直仍不变,平行不变,长度变,横竖不变,纵折半.
(3)画空间几何体的直观图,要注意选取适当的原点,建系画轴.
讲授新课
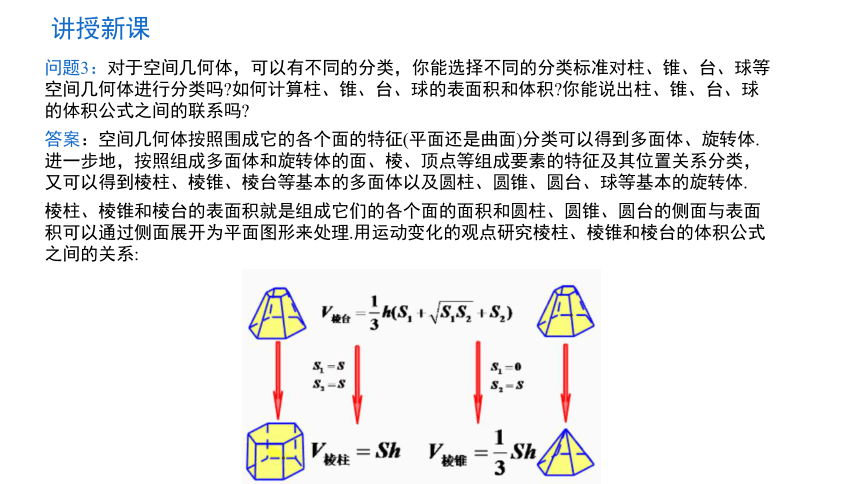
问题3:对于空间几何体,可以有不同的分类,你能选择不同的分类标准对柱、锥、台、球等空间几何体进行分类吗 如何计算柱、锥、台、球的表面积和体积 你能说出柱、锥、台、球的体积公式之间的联系吗
答案:空间几何体按照围成它的各个面的特征(平面还是曲面)分类可以得到多面体、旋转体.进一步地,按照组成多面体和旋转体的面、棱、顶点等组成要素的特征及其位置关系分类,又可以得到棱柱、棱锥、棱台等基本的多面体以及圆柱、圆锥、圆台、球等基本的旋转体.
棱柱、棱锥和棱台的表面积就是组成它们的各个面的面积和圆柱、圆锥、圆台的侧面与表面积可以通过侧面展开为平面图形来处理.用运动变化的观点研究棱柱、棱锥和棱台的体积公式之间的关系:
讲授新课
例3.如图所示,四边形是直角梯形,其中,AD∥BC,若将图中阴影部分绕旋转一周.
(1)求阴影部分形成的几何体的表面积.
(2)求阴影部分形成的几何体的体积
解:(1)由题意知所求旋转体的表面由三部分组成:圆台下底面、侧面和半球面,
,
,
.
故所求几何体的表面积为.
(2),
,
所求几何体体积为.
讲授新课
名师解惑
名师解惑:求空间几何体的表面积、体积的常见方法:
(1)公式法:根据题意直接套用表面积或体积公式求解.
(2)割补法:割补法的思想是通过分割或补形,将原几何体分割成或补成较易计算体积的几何体,从而求出原几何体的体积.
(3)等体积变换法:等积变换法的思想是从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理来求原几何体的体积.
讲授新课
问题4: 刻画平面的三个基本事实是立体几何公理体系的基石,是研究空间图形、进行逻辑推理的基础,实际上,三个基本事实刻画了平面的“平””,你能归纳一下刻画’、平面的“无限延展的方法吗
答案:平面的三个基本事实是按照从简单到复杂的顺序,刻画平面的基本性质.
基本事实1:从点与平面的关系角度刻画平面的唯一性.
基本事实2:从直线与平面的关系的角度,利用直线的“直”的属性,引无限延伸”画了平面的“平”和限延展”因的属性.
基本事实3:从平面与平面关系的角度,进一步说明了平面的“平”和“无限延展”的特征.
讲授新课
例4.如图,在四面体A-BCD中作截面PQR,若PQ与CB的延长线交于点M,
RQ与DB的延长线交于点N,RP与DC的延长线交于点K.
(1)求证:直线MN 平面PQR;
(2)求证:点K在直线MN上.
讲授新课
证明:(1)∵PQ 平面PQR,M∈直线PQ,
∴M∈平面PQR.
∵RQ 平面PQR,N∈直线RQ,
∴N∈平面PQR.
∴直线MN 平面PQR.
(2)∵M∈直线CB,CB 平面BCD,∴M∈平面BCD.
由(1)知M∈平面PQR,
∴M在平面PQR与平面BCD的交线上.
同理可知N,K也在平面PQR与平面BCD的交线上,
∴M,N,K三点共线,
∴点K在直线MN上.
讲授新课
名师解惑
名师解惑:证明点、线共面的方法
证明点、线共面的主要依据是基本事实1、基本事实2及其推论,常用的方法有:
(1)辅助平面法,先证明有关点、线确定平面α,再证明其余点、线确定平面β,最后证明平面α,β重合;
(2)纳入平面法,先由条件确定一个平面,再证明有关的点、线在此平面内.
讲授新课
例5.如图:在正方体中,E为DD1的中点.
(1)求证:平面;
(2)若F为CC1的中点,求证:平面平面.
证明:(1)连结交于O,连结.
∵因为为正方体,底面为正方形,
对角线 交于O点,所以O为的中点,
又因为E为DD1的中点,在中
∴是的中位线
∴;
又因为平面,平面,所以平面.
(2)证明:
因为F为CC1的中点,E为DD1的中点,所以,
所以四边形为平行四边形,所以,
又因为平面,平面,所以∥平面;
由(1)知平面,又因为,所以平面平面.
讲授新课
名师解惑
名师解惑:空间中的平行关系主要是指空间中线与线、线与面及面与面的平行,其中三种关系相互渗透.在解决线面、面面平行问题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而利用性质定理时,其顺序相反,且“高维”的性质定理就是“低维”的判定定理.特别注意,转化的方法总是由具体题目的条件决定,不能过于呆板僵化,要遵循规律而不局限于规律.如下图所示是平行关系相互转化的示意图.
讲授新课
例6.如图,在三棱柱中,侧棱⊥底面,,分别为棱的中点.
(1)求证:平面;
(2)求证:;
(3)若求三棱锥的体积.
解析:(1)证明:因为侧棱⊥底面,平面,所以,
因为为中点,,故,而,
故平面,
(2)证明:由(1)知平面,而平面,故.
讲授新课
例6.如图,在三棱柱中,侧棱⊥底面,,分别为棱的中点.
(1)求证:平面;
(2)求证:;
(3)若求三棱锥的体积.
(3)解:取的中点为,连接.
因为,故,故,
因为,故,且,故,
因为三棱柱中,侧棱⊥底面,
故三棱柱为直棱柱,故⊥底面,
因为底面,故,而,
故平面,
而,
故.
讲授新课
名师解惑
名师解惑:1.空间垂直关系的判定方法:
(1)判定线线垂直的方法有:
①计算所成的角为90°(包括平面角和异面直线所成的角);
②由线面垂直的性质(若a⊥α,b α,则a⊥b);
③面面垂直的定义:若两平面垂直,则两平面相交形成的二面角的平面角为90°.
讲授新课
名师解惑
名师解惑:1.空间垂直关系的判定方法:
(2)判定线面垂直的方法有:
①线面垂直的定义(一般不易验证任意性);
②线面垂直的判定定理(a⊥b,a⊥c,b α,c α,b∩c=M a⊥α);
③平行线垂直平面的传递性质(a∥b,b⊥α a⊥α);
④面面垂直的性质(α⊥β,α∩β=l,a β,a⊥l a⊥α);
⑤面面平行的性质(a⊥α,α∥β a⊥β);
⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ l⊥γ).
讲授新课
名师解惑
名师解惑:1.空间垂直关系的判定方法:
(3)面面垂直的判定方法有:
①根据定义(作两平面构成的二面角的平面角,计算其为90°);
②面面垂直的判定定理(a⊥β,a α α⊥β).
2.垂直关系的转化是:
评价反馈
1.已知圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( )
A.120° B.150°
C.180° D.240°
C
C 解析:设圆锥底面半径为r,母线为l,则πrl+πr2=3πr2,得l=2r,∴展开图扇形半径为2r,弧长为2πr.∴展开图是半圆.∴扇形的圆心角为180°.故选C.
评价反馈
2.中国古代数学瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该几何体为上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,其中AA1,BB1,CC1,DD1是柱体的高,底面扇环所对的圆心角为,的长度为的长度的2倍,AA1=4,CD=1,则该曲池的体积为( )
A.3π B.4π
C.5π D.6π
B
B解析:不妨设弧AD所在圆的半径为R,弧BC所在圆的半径为r,由弧长度为弧长度的2倍,可知R=2r,又CD=R-r=r=1,所以r=1,R=2,
故该曲池的体积V×(R2-r2)×4=4π.故选B.
评价反馈
3.有一块多边形菜地,它的水平放置的平面图形的斜二测直观图是直角梯形ABCD(如图),其中∠ABC=45°,AD=CD=1,BC⊥CD,则这块菜地的面积为( )
A. B.
C. D.3
D
D解析:如图①所示,过点A作AE垂直于BC于点E,
∵∠ABC=45°,AD=CD=1,
∴BE=AE=CD=1,四边形AECD是正方形,则BC=2,AB,
将斜二测直观图还原成图②所示直角梯形,其中A'B'=2,A'D'=1,B'C'=2,
∴这块菜地的面积为3.故选D.
评价反馈
4.已知直线l⊥平面α,直线m 平面β,有下面四个命题:
①α∥β l⊥m;②α⊥β l∥m;
③l∥m α⊥β;④l⊥m α∥β.
其中正确的两个命题是( )
A.①与② B.①与③
C.②与④ D.③与④
B
B 解析:因为直线l⊥平面α,直线m 平面β,若α∥β,则l⊥β,l⊥m,①正确;
若α⊥β,则l∥β或l β,l,m的位置不确定,②不正确;
若l∥m,则m⊥α,所以α⊥β,③正确;
若l⊥m,则m∥α或m α,则α,β相交或平行,④不正确.故选B.
评价反馈
5.(2024·山东潍坊高一期末)如图,圆台OO1的侧面展开图扇环的圆心角为180°,其中SA=2,SB=4,则该圆台的高为( )
A.1 B.
C. D.4
C
C解析:因为圆台OO1的侧面展开图扇环的圆心角为180°,
所以在圆锥SO1中,有2π·AO1×2×π·SA=2π,所以AO1=1,
又在圆锥SO中有,2π·OB×2×π·SB=4π,
所以OB=2,所以该圆台的高为
h
.
故选C.
评价反馈
6.在四面体A-BCD中,已知棱AC的长为,其余各棱长都为1,则二面角A-CD-B的余弦值为( )
A. B. C. D.
C
C解析:取AC的中点E,CD的中点F,连接BE,EF,BF,则∠BFE即为二面角A-CD-B的平面角,
且EF,BE,BF.
因为EF2+BE2=BF2,
所以△BEF为直角三角形,cos∠BFE.故选C.
评价反馈
7.如图,在棱长均为2的直三棱柱ABC-A1B1C1中,D是A1B1的中点,过B,C,D三点的平面将该三棱柱截成两部分,则顶点B1所在部分的体积为( )
A. B.
C. D.
B
评价反馈
B 解析:设平面BCD交A1C1于点E,连接DE,CE,
在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面BCD∩平面ABC=BC,
平面BCD∩平面A1B1C1=DE,所以DE∥BC.
又因为BB1∥CC1且BB1=CC1,故四边形BB1C1C为平行四边形,所以BC∥B1C1,
所以DE∥B1C1.
因为D为A1B1的中点,所以E为A1C1的中点,且DEB1C1=1.
因为直三棱柱ABC-A1B1C1的每条棱长都为2,
则S△ABC·AA1×22×2=2,
易知△A1DE是边长为1的等边三角形,
则×12,
(+S△ABC+)·AA1
××2,
所以所求体积V=2-.故选B.
课堂小结
总结归纳
正方体(或长方体)是重要的几何体模型我们要深入研究正方体模型,对它进行变形,构建出新的模型,探求各种空间位置关系或几何模型与正方体之间的联系,彰显正方体的“母体地位.
布置作业
1.认真整理本节所讲知识,梳理知识脉络,完成学案的核心素养专练;
2.必做题:教科书P169复习参考题1-9.
选做题:教科书P170复习参考题15,16.
谢谢大家
第八章末小结
第1课时
第八章 空间点、直线、平面之间的位置关系
数学
学习目标
①在回顾与思考本章的主要内容的基础上,引导学生梳理立体几何的核心概念、定理等内容与思想方法,构建立体几何的核心体系,体会研究空间图形的基本思路:直观感知、操作确认、推理论证、度量计算.
②借助分析典型问题的通性通法,通过“图”(识图、画图、用图)提升学生直观想象素养,通过“写”(图形、文字、符号三种语言)培养学生逻辑推理能力,通过“悟”(直观感知、操作确认)发展学生数学抽象水平.
学习重难点
重点:
通过分析常见几何图形及典型问题,梳理立体几何初步的核心概念、定理等内容与思想方法,从而构建立体几何的核心体系.
难点:
分析组合体的结构特征以及运用有关定理推理证明一些几何元素间的位置关系.
导入新课
一、你能梳理本章的知识结构吗?
导入新课
二、核心知识归纳:问题与思考
问题1:我们是从哪些角度入手研究基本几何体的结构特征的 你能用基本几何体的结构特征解释身边物体的结构吗 请举例说明.
答案:我们从对空间几何体(实物、模型、图片等)的整体观察入手,认识多面体、旋转体以及一些基本几何体(棱柱、棱锥、棱台、圆柱、圆锥、圆台、球)的结构特征,研究这些几何体的组成元素及其相互关系.
导入新课
二、核心知识归纳:问题与思考
问题1:我们是从哪些角度入手研究基本几何体的结构特征的 你能用基本几何体的结构特征解释身边物体的结构吗 请举例说明.
答案:我们从对空间几何体(实物、模型、图片等)的整体观察入手,认识多面体、旋转体以及一些基本几何体(棱柱、棱锥、棱台、圆柱、圆锥、圆台、球)的结构特征,研究这些几何体的组成元素及其相互关系.
讲授新课
例1(1)(2020课标Ⅰ.理)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥,以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )
A. B.
C. D.
C
答案:C.
解析:如图,设,则,
由题意,即,化简得,
解得(负值舍去).故选C.
讲授新课
(2)将长与宽分别为6和4的矩形卷成一个圆柱(无重叠部分),则该圆柱的底面半径为________.
或
解析:(1)若以6为底面圆周长,则,;
(2)若以4为底面圆周长,则,
讲授新课
问题2:利用斜二测画法可以画出空间几何体的直观图,你能结合实例说出用斜二测画法画空间几何体的直观图的基本步吗
答案:斜二测画法画空间几何体的直观图,是用平面图形表示空间图形的重要方法,我们能够根据直观图想象空间几何体的形状和结构.简单说,斜二测画法的规则是:横竖不变,纵减半,平行性不变.
OC=2O'C'=2,
讲授新课
例2(2024·浙江G5联盟高一期中联考)已知水平放置的四边形ABCD的斜二测直观图为矩形A'B'C'D',已知A'B'=2,B'C'=1,则四边形ABCD的面积为( )
A.2 B.4
C.6 D.8
C
答案:B
解析: 因为A'B'=2,B'C'=1,取A'B'的中点O'为坐标原点,以O'C'为y'轴建立坐标系O'x'y'如左图.
因为斜二测直观图为矩形A'B'C'D',A'O'=O'B'=1,B'C'=1,
则O'C',
可得原图ABCD(右图)中,AB=A'B'=2,
所以四边形的面积为AB·OC=2×24.
故选B.
讲授新课
名师解惑
名师解惑:利用斜二测画法画空间几何体的直观图的注意点
(1)画空间几何体的直观图在要求不太严格的情况下,长度和角度可适当选取.为了增强立体感,被挡住的部分通常用虚线表示.
(2)画法规则可简记为:两轴夹角为45°,竖轴垂直仍不变,平行不变,长度变,横竖不变,纵折半.
(3)画空间几何体的直观图,要注意选取适当的原点,建系画轴.
讲授新课
问题3:对于空间几何体,可以有不同的分类,你能选择不同的分类标准对柱、锥、台、球等空间几何体进行分类吗 如何计算柱、锥、台、球的表面积和体积 你能说出柱、锥、台、球的体积公式之间的联系吗
答案:空间几何体按照围成它的各个面的特征(平面还是曲面)分类可以得到多面体、旋转体.进一步地,按照组成多面体和旋转体的面、棱、顶点等组成要素的特征及其位置关系分类,又可以得到棱柱、棱锥、棱台等基本的多面体以及圆柱、圆锥、圆台、球等基本的旋转体.
棱柱、棱锥和棱台的表面积就是组成它们的各个面的面积和圆柱、圆锥、圆台的侧面与表面积可以通过侧面展开为平面图形来处理.用运动变化的观点研究棱柱、棱锥和棱台的体积公式之间的关系:
讲授新课
例3.如图所示,四边形是直角梯形,其中,AD∥BC,若将图中阴影部分绕旋转一周.
(1)求阴影部分形成的几何体的表面积.
(2)求阴影部分形成的几何体的体积
解:(1)由题意知所求旋转体的表面由三部分组成:圆台下底面、侧面和半球面,
,
,
.
故所求几何体的表面积为.
(2),
,
所求几何体体积为.
讲授新课
名师解惑
名师解惑:求空间几何体的表面积、体积的常见方法:
(1)公式法:根据题意直接套用表面积或体积公式求解.
(2)割补法:割补法的思想是通过分割或补形,将原几何体分割成或补成较易计算体积的几何体,从而求出原几何体的体积.
(3)等体积变换法:等积变换法的思想是从不同的角度看待原几何体,通过改变顶点和底面,利用体积不变的原理来求原几何体的体积.
讲授新课
问题4: 刻画平面的三个基本事实是立体几何公理体系的基石,是研究空间图形、进行逻辑推理的基础,实际上,三个基本事实刻画了平面的“平””,你能归纳一下刻画’、平面的“无限延展的方法吗
答案:平面的三个基本事实是按照从简单到复杂的顺序,刻画平面的基本性质.
基本事实1:从点与平面的关系角度刻画平面的唯一性.
基本事实2:从直线与平面的关系的角度,利用直线的“直”的属性,引无限延伸”画了平面的“平”和限延展”因的属性.
基本事实3:从平面与平面关系的角度,进一步说明了平面的“平”和“无限延展”的特征.
讲授新课
例4.如图,在四面体A-BCD中作截面PQR,若PQ与CB的延长线交于点M,
RQ与DB的延长线交于点N,RP与DC的延长线交于点K.
(1)求证:直线MN 平面PQR;
(2)求证:点K在直线MN上.
讲授新课
证明:(1)∵PQ 平面PQR,M∈直线PQ,
∴M∈平面PQR.
∵RQ 平面PQR,N∈直线RQ,
∴N∈平面PQR.
∴直线MN 平面PQR.
(2)∵M∈直线CB,CB 平面BCD,∴M∈平面BCD.
由(1)知M∈平面PQR,
∴M在平面PQR与平面BCD的交线上.
同理可知N,K也在平面PQR与平面BCD的交线上,
∴M,N,K三点共线,
∴点K在直线MN上.
讲授新课
名师解惑
名师解惑:证明点、线共面的方法
证明点、线共面的主要依据是基本事实1、基本事实2及其推论,常用的方法有:
(1)辅助平面法,先证明有关点、线确定平面α,再证明其余点、线确定平面β,最后证明平面α,β重合;
(2)纳入平面法,先由条件确定一个平面,再证明有关的点、线在此平面内.
讲授新课
例5.如图:在正方体中,E为DD1的中点.
(1)求证:平面;
(2)若F为CC1的中点,求证:平面平面.
证明:(1)连结交于O,连结.
∵因为为正方体,底面为正方形,
对角线 交于O点,所以O为的中点,
又因为E为DD1的中点,在中
∴是的中位线
∴;
又因为平面,平面,所以平面.
(2)证明:
因为F为CC1的中点,E为DD1的中点,所以,
所以四边形为平行四边形,所以,
又因为平面,平面,所以∥平面;
由(1)知平面,又因为,所以平面平面.
讲授新课
名师解惑
名师解惑:空间中的平行关系主要是指空间中线与线、线与面及面与面的平行,其中三种关系相互渗透.在解决线面、面面平行问题时,一般遵循从“低维”到“高维”的转化,即从“线线平行”到“线面平行”,再到“面面平行”;而利用性质定理时,其顺序相反,且“高维”的性质定理就是“低维”的判定定理.特别注意,转化的方法总是由具体题目的条件决定,不能过于呆板僵化,要遵循规律而不局限于规律.如下图所示是平行关系相互转化的示意图.
讲授新课
例6.如图,在三棱柱中,侧棱⊥底面,,分别为棱的中点.
(1)求证:平面;
(2)求证:;
(3)若求三棱锥的体积.
解析:(1)证明:因为侧棱⊥底面,平面,所以,
因为为中点,,故,而,
故平面,
(2)证明:由(1)知平面,而平面,故.
讲授新课
例6.如图,在三棱柱中,侧棱⊥底面,,分别为棱的中点.
(1)求证:平面;
(2)求证:;
(3)若求三棱锥的体积.
(3)解:取的中点为,连接.
因为,故,故,
因为,故,且,故,
因为三棱柱中,侧棱⊥底面,
故三棱柱为直棱柱,故⊥底面,
因为底面,故,而,
故平面,
而,
故.
讲授新课
名师解惑
名师解惑:1.空间垂直关系的判定方法:
(1)判定线线垂直的方法有:
①计算所成的角为90°(包括平面角和异面直线所成的角);
②由线面垂直的性质(若a⊥α,b α,则a⊥b);
③面面垂直的定义:若两平面垂直,则两平面相交形成的二面角的平面角为90°.
讲授新课
名师解惑
名师解惑:1.空间垂直关系的判定方法:
(2)判定线面垂直的方法有:
①线面垂直的定义(一般不易验证任意性);
②线面垂直的判定定理(a⊥b,a⊥c,b α,c α,b∩c=M a⊥α);
③平行线垂直平面的传递性质(a∥b,b⊥α a⊥α);
④面面垂直的性质(α⊥β,α∩β=l,a β,a⊥l a⊥α);
⑤面面平行的性质(a⊥α,α∥β a⊥β);
⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ l⊥γ).
讲授新课
名师解惑
名师解惑:1.空间垂直关系的判定方法:
(3)面面垂直的判定方法有:
①根据定义(作两平面构成的二面角的平面角,计算其为90°);
②面面垂直的判定定理(a⊥β,a α α⊥β).
2.垂直关系的转化是:
评价反馈
1.已知圆锥的表面积是底面积的3倍,那么该圆锥的侧面展开图扇形的圆心角为( )
A.120° B.150°
C.180° D.240°
C
C 解析:设圆锥底面半径为r,母线为l,则πrl+πr2=3πr2,得l=2r,∴展开图扇形半径为2r,弧长为2πr.∴展开图是半圆.∴扇形的圆心角为180°.故选C.
评价反馈
2.中国古代数学瑰宝《九章算术》中记载了一种称为“曲池”的几何体,该几何体为上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,其中AA1,BB1,CC1,DD1是柱体的高,底面扇环所对的圆心角为,的长度为的长度的2倍,AA1=4,CD=1,则该曲池的体积为( )
A.3π B.4π
C.5π D.6π
B
B解析:不妨设弧AD所在圆的半径为R,弧BC所在圆的半径为r,由弧长度为弧长度的2倍,可知R=2r,又CD=R-r=r=1,所以r=1,R=2,
故该曲池的体积V×(R2-r2)×4=4π.故选B.
评价反馈
3.有一块多边形菜地,它的水平放置的平面图形的斜二测直观图是直角梯形ABCD(如图),其中∠ABC=45°,AD=CD=1,BC⊥CD,则这块菜地的面积为( )
A. B.
C. D.3
D
D解析:如图①所示,过点A作AE垂直于BC于点E,
∵∠ABC=45°,AD=CD=1,
∴BE=AE=CD=1,四边形AECD是正方形,则BC=2,AB,
将斜二测直观图还原成图②所示直角梯形,其中A'B'=2,A'D'=1,B'C'=2,
∴这块菜地的面积为3.故选D.
评价反馈
4.已知直线l⊥平面α,直线m 平面β,有下面四个命题:
①α∥β l⊥m;②α⊥β l∥m;
③l∥m α⊥β;④l⊥m α∥β.
其中正确的两个命题是( )
A.①与② B.①与③
C.②与④ D.③与④
B
B 解析:因为直线l⊥平面α,直线m 平面β,若α∥β,则l⊥β,l⊥m,①正确;
若α⊥β,则l∥β或l β,l,m的位置不确定,②不正确;
若l∥m,则m⊥α,所以α⊥β,③正确;
若l⊥m,则m∥α或m α,则α,β相交或平行,④不正确.故选B.
评价反馈
5.(2024·山东潍坊高一期末)如图,圆台OO1的侧面展开图扇环的圆心角为180°,其中SA=2,SB=4,则该圆台的高为( )
A.1 B.
C. D.4
C
C解析:因为圆台OO1的侧面展开图扇环的圆心角为180°,
所以在圆锥SO1中,有2π·AO1×2×π·SA=2π,所以AO1=1,
又在圆锥SO中有,2π·OB×2×π·SB=4π,
所以OB=2,所以该圆台的高为
h
.
故选C.
评价反馈
6.在四面体A-BCD中,已知棱AC的长为,其余各棱长都为1,则二面角A-CD-B的余弦值为( )
A. B. C. D.
C
C解析:取AC的中点E,CD的中点F,连接BE,EF,BF,则∠BFE即为二面角A-CD-B的平面角,
且EF,BE,BF.
因为EF2+BE2=BF2,
所以△BEF为直角三角形,cos∠BFE.故选C.
评价反馈
7.如图,在棱长均为2的直三棱柱ABC-A1B1C1中,D是A1B1的中点,过B,C,D三点的平面将该三棱柱截成两部分,则顶点B1所在部分的体积为( )
A. B.
C. D.
B
评价反馈
B 解析:设平面BCD交A1C1于点E,连接DE,CE,
在三棱柱ABC-A1B1C1中,平面ABC∥平面A1B1C1,平面BCD∩平面ABC=BC,
平面BCD∩平面A1B1C1=DE,所以DE∥BC.
又因为BB1∥CC1且BB1=CC1,故四边形BB1C1C为平行四边形,所以BC∥B1C1,
所以DE∥B1C1.
因为D为A1B1的中点,所以E为A1C1的中点,且DEB1C1=1.
因为直三棱柱ABC-A1B1C1的每条棱长都为2,
则S△ABC·AA1×22×2=2,
易知△A1DE是边长为1的等边三角形,
则×12,
(+S△ABC+)·AA1
××2,
所以所求体积V=2-.故选B.
课堂小结
总结归纳
正方体(或长方体)是重要的几何体模型我们要深入研究正方体模型,对它进行变形,构建出新的模型,探求各种空间位置关系或几何模型与正方体之间的联系,彰显正方体的“母体地位.
布置作业
1.认真整理本节所讲知识,梳理知识脉络,完成学案的核心素养专练;
2.必做题:教科书P169复习参考题1-9.
选做题:教科书P170复习参考题15,16.
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
