第九章 9.2.3总体集中趋势的估计--人教A版高中数学必修第二册教学课件(共32张PPT)
文档属性
| 名称 | 第九章 9.2.3总体集中趋势的估计--人教A版高中数学必修第二册教学课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 910.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
9.2.3总体集中趋势的估计
第九章 统计
数学
学习目标
1.通过实例,理解集中趋势参数的统计含义,能用样本估计总体的集中趋势参数(众数、中位数、平均数),培养直观想象素养.
2.通过典型例题,能正确求解样本数据的众数、中位数、平均数.
3.通过对平均数、中位数、众数的学习,提升数学抽象、数学运算的核心素养.
学习重难点
重点:
1.求样本数据的众数、中位数、平均数.
2. 利用样本的集中趋势估计总体的集中趋势.
难点:
1. 对于不同数据类型正确选择描述总体集中趋势的统计量.
2. 利用频率直方图估计总体的集中趋势.
3. 对数据陷阱的理解.
课堂导入
在初中,我们已对平均数、中位数、众数有一定的学习,请大家先看三个实例,并将三个特征量填在合适的位置上.
一、创设情境,复习导入
问题1
a.某服装专业学生需设计一款均码的女装,应该关心女性人群服装尺码的 .
b.商场销售部门给营业员制定销售指标,需至少有一半人能完成任务,需要参考以往营业员销售额的 .
c.跳水比赛中,选手更关心成绩的 .
众数
中位数
平均数
课堂导入
一、创设情境,复习导入
问题2:平均数、中位数、众数,这三个特征量它们有什么共同点?
它们从不同角度刻画了总体的“中心位置”,平均数从数值中心的角度进行总体集中趋势的估计,而中位数、众数则是从位置中心的角度进行总体集中趋势的估计.
课堂
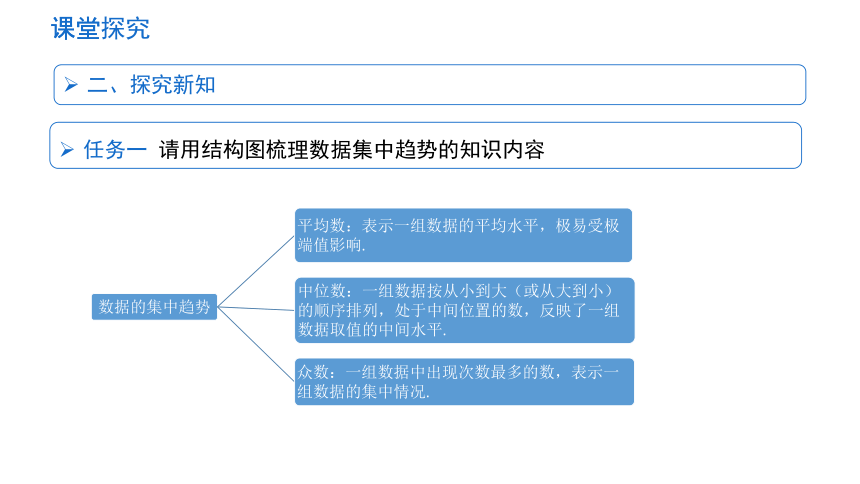
任务一 请用结构图梳理数据集中趋势的知识内容
课堂探究
二、探究新知
课堂
任务二 探究平均数和中位数的联系与区别
课堂探究
探究:利用9.2.1节中100户居民用户的月均用水量的调查数据,
(1)请同学们计算这组数据的平均数和中位数.
(2)假设有2 000户居民用户,你能估计该小区的月均用水总量吗?
(3)小明用统计软件计算了这100 户居民月用水量的平均数和中位数,但录入数据时把一个数据7.7录成了77.请计算录入数据的平均数和中位数,与真实的样本平均数和中位数作比较.哪个量变化更大?请说明理由.
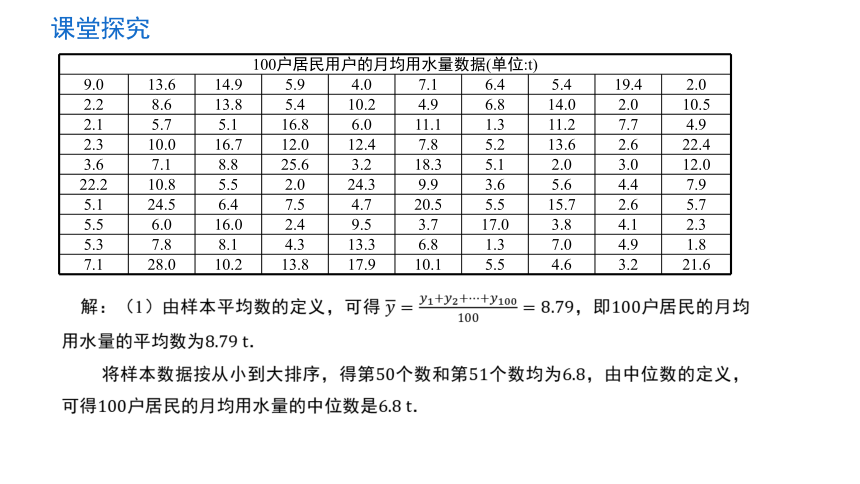
课堂探究
解:(1)由样本平均数的定义,可得 ,即户居民的月均用水量的平均数为.
将样本数据按从小到大排序,得第个数和第个数均为,由中位数的定义,可得户居民的月均用水量的中位数是.
100户居民用户的月均用水量数据(单位:t) 9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
(3)通过计算可以发现,平均数由原来的8.79 t变为9.483 t,中位数没有变化,还是6.8 t.这是因为样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
课堂探究
总结:
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
(2)假设有2 000户,该小区月均用水总量为.
课堂探究
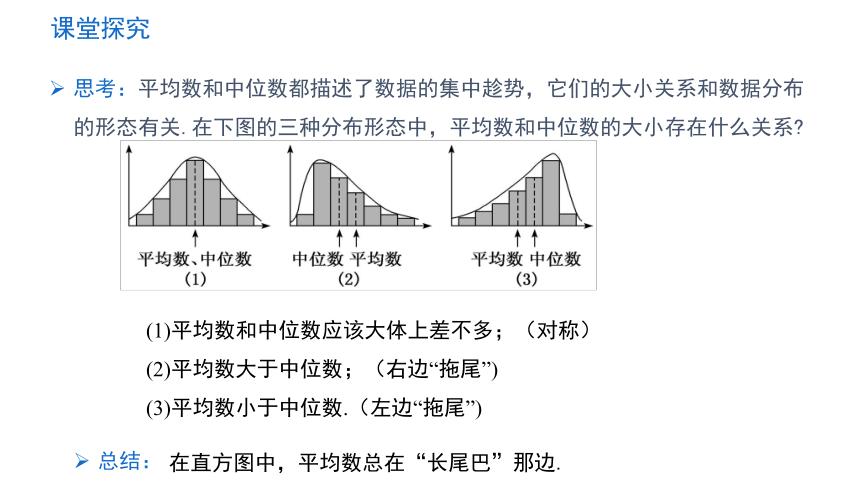
思考:平均数和中位数都描述了数据的集中趁势,它们的大小关系和数据分布的形态有关.在下图的三种分布形态中,平均数和中位数的大小存在什么关系
(1)平均数和中位数应该大体上差不多;(对称)
(2)平均数大于中位数;(右边“拖尾”)
(3)平均数小于中位数.(左边“拖尾”)
总结:
在直方图中,平均数总在“长尾巴”那边.
课堂
任务三 探究众数
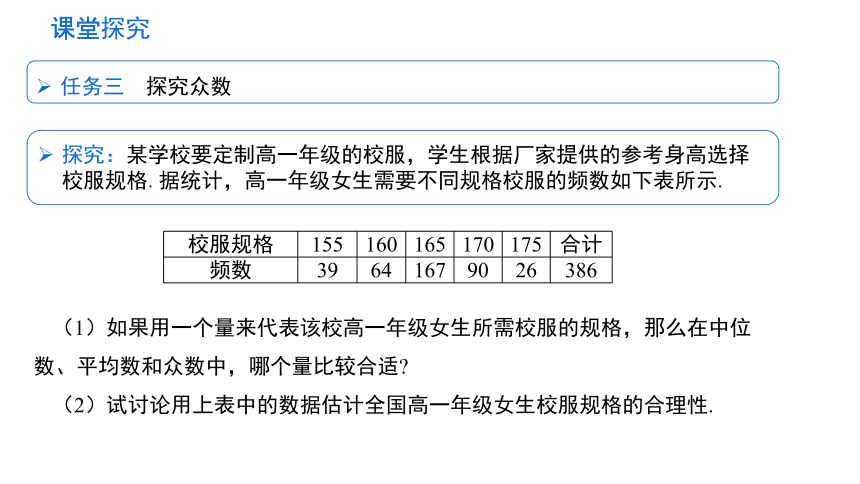
课堂探究
探究:某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如下表所示.
(1)如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适
(2)试讨论用上表中的数据估计全国高一年级女生校服规格的合理性.
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
解:(1)为了更直观地观察数据的特征,我们用条形图表示表中的数据(如右图).可以发现,选择校服规格为“165”的女生的频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
课堂探究
总结:
一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
(2)由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
课堂
任务四 探究利用频率分布直方图估计数据的集中趋势
课堂探究
说一说:我们在报纸、网络上获得的往往是已经整理好的统计表或统计图.
是否可以估计样本的平均数、中位数和众数
可以估算,在频率分布直方图中,我们无法知道每个组内的数据是如何分布的.此时,通常假设它们在组内均匀分布,这样就可以获得样本的平均数、中位数和众数的近似估计,进而估计总体的平均数、中位数和众数.
思考
你能以下图中频率分布直方图提供的信息为例,给出估计方法吗?(小组交流)
众数:最高矩形的中点横坐标.
课堂探究
中位数:左边和右边的直方图的面积应该相等.
样本平均数:可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和 近似代替.
解:平均数的近似值
为
这个结果与根据原始数据计算的样本平均数8.79相差不大.
由于,因此中位数落在区间内;
设中位数为,由,
得到因此,中位数约为6.71,这个结果与根据原始数据求得的中位数6.8很接近.
平均数为8.96大于中位数6.71,符合右边“拖尾”的特点,即平均数大于中位数.
在频率分布直方图中,月均用水量在区间[4.2,7.2)内的居民最多,可以将这个区间的中点5.7作为众数的估计值.
课堂探究
课堂探究
各抒己见 假设你到人力市场去找工作,有一个企业老板告诉你,“我们企业员工的年平均收入是20万元”,你该如何理解这句话
以下方甲、乙两家10人公司为例,观察两组数据,你发现了什么?
员工编号 1 2 3 4 5 6 7 8 9 10
年收入/万元 20 21 19 23 21 20 16 20 22 18
甲公司员工年平均收入情况表
乙公司员工年平均收入情况表
员工编号 1 2 3 4 5 6 7 8 9 10
年收入/万元 5 10 120 7 8 15 10 15 5 5
课堂探究
归纳总结
对平均数、中位数、众数做比较
课堂
课堂探究
三、应用举例
【例1】根据如图所示的频率分布直方图求出样本数据的众数、中位数和平均数.
解:在中的数据最多,取这个区间的中点值作为众数的近似 值,得众数约为125.5.
中位数左边和右边的直方图的面积相等,设中位数为x,
则由图可知x,则
解得,即中位数约为125.75.
使用组中值求平均数,
即平均数约为125.8.
课堂
课堂探究
三、应用举例
【例2】据了解,某公司的33名职工月工资(单位:元)如下:
职务 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 11 000 10 000 9 000 8 000 6 500 5 500 4 000
(1) 求该公司职工月工资的平均数、中位数、众数(精确到1);
(2) 假设副董事长的工资从10 000元提升到20 000元,董事长的工资从11 000元提升到30 000元,那么新的平均数、中位数、众数又是多少(精确到整数)
(3) 你认为哪个统计量更能反映这个公司员工的工资水平 结合此问题谈一谈你的看法.
解:(1)平均数是(元).
中位数是4 000元,众数是4 000元.
(2) 平均数是(元).
中位数是4 000元,众数是4 000元.
(3) 在这个问题中,中位数和众数均能反映该公司员工的工资水平,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数偏差较大,所以平均数不能准确反映这个公司员工的工资水平.
课堂探究
归纳新知
众数、中位数、平均数的应用特点
(1)平均数与每一个数据都有关,可以反映更多的总体信息,但受极端值的影响大.
(2)中位数是样本数据所占频率的等分线,不受极端值的影响,当一组数据中存在极端值时,可用中位数描述这组数据的集中趋势.
(3)众数只能体现数据的最大集中点,无法客观反映总体特征.
课堂探究
评价反馈
1.一组样本数据为:19,23,12,14,14,17,10,12,18,14,27,则这组数据的众数和中位数分别为( )
14,14 B. 12,14
C. 14, D. 12,
解析:把这组数据按从小到大排列为10,12,12,14,14,14,17,18,19,23,27,则可知其众数为14,中位数为14.
A
评价反馈
解析:众数是指出现次数最多的数据,所以,将这组数据按从小到大的顺序排列:,6,6,8,12,中位数是指处于中间位置的数,即为6,平均数为
.故选.
2.(多选)已知一组数据为,6,8,,12,且这组数据的众数为6,那么下列说法正确的是( )
数据的中位数是6 B. 数据的平均数是6
C. D.
评价反馈
解析:最高分为94,若8为最低分,则平均分为,故最低分为88.设看不见的个位数为,则去掉最高分94和最低分88,平均分为,解得,故该数为89.
89
3.在一次比赛上,9位评委给参赛选手甲打出的分数为88,89,8●,93,92,91,92,91,94.去掉一个最高分和一个最低分后,算得平均分为91,参赛选手复查时,发现有一个数的个位数字无法看清.若成绩计算无误,则该数为 .
评价反馈
4.(多选)甲、乙两名射击运动员在某次测试中各射击20次,两人测试成绩的条形图如图所示,则下列说法正确的是( )
A.甲运动员测试成绩的中位数等于乙运动员测试成绩的中位数
B.甲运动员测试成绩的众数大于乙运动员测试成绩的众数
C.甲运动员测试成绩的平均数大于乙运动员测试成绩的平均数
D.甲运动员测试成绩的第90百分位数等于乙运动员测试成绩的第90百分位数
AD
解析:
甲运动员测试成绩:3次7环,8次8环,5次9环,4次10环.所以中位数为8,众数为8,平均数为=8.5,第90百分位数为10.
乙运动员测试成绩:4次7环,7次8环,4次9环,5次10环.所以中位数为8,众数为8,平均数为=8.5,第90百分位数为10.故选AD.
评价反馈
解析:设丢失的数据为x,则这七个数据的平均数为,众数是4,因为这组数据的平均数与众数的和是中位数的2倍,若x≤4,则中位数为4,此时+4=2×4,解得x=-9;若4<x<7,则中位数为x,此时+4=2x,解得x=5;若x≥7,则中位数为7,此时+4=2×7,解得x=33.综上可知,丢失数据的所有可能的取值为-9,5,33,其构成的集合为{-9,5,33}.
评价反馈
5.(2024·绍兴月考)已知一组数据丢失了其中一个,剩下的六个数据分别是4,4,7,4,8,10,若这组数据的平均数与众数的和是中位数的2倍,则丢失数据的所有可能值组成的集合为 .
{-9,5,33}
评价反馈
6.某校高一年级举行了一次数学竞赛,为了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n),按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,已知得分在[50,60),[90,100]内的频数分别为8,2.
(1)求样本容量n 和频率分布直方图中的x,y 的值;
(2)估计本次竞赛学生成绩的众数、中位数、平均数.
评价反馈
解:(1)由题意可知,样本容量n==50,
y==0.004,
x=0.1-0.016-0.040-0.010-0.004=0.030.
(2)由题中频率分布直方图可知,本次竞赛学生成绩的众数约为75.
设中位数为m,
∵(0.016+0.030)×10<0.5<(0.016+0.030+0.040)×10,则m∈[70,80),
∴(0.016+0.030)×10+(m-70)×0.040=0.5,
解得m=71,即本次竞赛学生成绩的中位数约为71.
本次竞赛学生成绩的平均数约为55×0.16+65×0.3+75×0.4+85×0.1+95×0.04=70.6.
课堂小结
通过本节课学习,你收获了哪些新知识与技能?通过什么方法学到的?体会到了什么数学思想?
1.已学习:众数、中位数、平均数的计算及总体集中趋势的估计.
2.须贯通:众数、中位数、平均数是真实数据的估计值,描述了真实数据的集 中趋势,在频率分布直方图中求这些数字特征时应用了数形结合的思想.
3.应注意:(1)一组数据的众数可能有一个、多个或不存在;
(2)求中位数时,应先将数据从小到大或从大到小排列.
布置作业
认真整理本节所讲知识,梳理知识脉络,完成学案的核心素养专练;
必做题:课本209页练习3、课本217页习题第9题.
选做题:课本225页复习参考题第11题
谢谢大家
9.2.3总体集中趋势的估计
第九章 统计
数学
学习目标
1.通过实例,理解集中趋势参数的统计含义,能用样本估计总体的集中趋势参数(众数、中位数、平均数),培养直观想象素养.
2.通过典型例题,能正确求解样本数据的众数、中位数、平均数.
3.通过对平均数、中位数、众数的学习,提升数学抽象、数学运算的核心素养.
学习重难点
重点:
1.求样本数据的众数、中位数、平均数.
2. 利用样本的集中趋势估计总体的集中趋势.
难点:
1. 对于不同数据类型正确选择描述总体集中趋势的统计量.
2. 利用频率直方图估计总体的集中趋势.
3. 对数据陷阱的理解.
课堂导入
在初中,我们已对平均数、中位数、众数有一定的学习,请大家先看三个实例,并将三个特征量填在合适的位置上.
一、创设情境,复习导入
问题1
a.某服装专业学生需设计一款均码的女装,应该关心女性人群服装尺码的 .
b.商场销售部门给营业员制定销售指标,需至少有一半人能完成任务,需要参考以往营业员销售额的 .
c.跳水比赛中,选手更关心成绩的 .
众数
中位数
平均数
课堂导入
一、创设情境,复习导入
问题2:平均数、中位数、众数,这三个特征量它们有什么共同点?
它们从不同角度刻画了总体的“中心位置”,平均数从数值中心的角度进行总体集中趋势的估计,而中位数、众数则是从位置中心的角度进行总体集中趋势的估计.
课堂
任务一 请用结构图梳理数据集中趋势的知识内容
课堂探究
二、探究新知
课堂
任务二 探究平均数和中位数的联系与区别
课堂探究
探究:利用9.2.1节中100户居民用户的月均用水量的调查数据,
(1)请同学们计算这组数据的平均数和中位数.
(2)假设有2 000户居民用户,你能估计该小区的月均用水总量吗?
(3)小明用统计软件计算了这100 户居民月用水量的平均数和中位数,但录入数据时把一个数据7.7录成了77.请计算录入数据的平均数和中位数,与真实的样本平均数和中位数作比较.哪个量变化更大?请说明理由.
课堂探究
解:(1)由样本平均数的定义,可得 ,即户居民的月均用水量的平均数为.
将样本数据按从小到大排序,得第个数和第个数均为,由中位数的定义,可得户居民的月均用水量的中位数是.
100户居民用户的月均用水量数据(单位:t) 9.0 13.6 14.9 5.9 4.0 7.1 6.4 5.4 19.4 2.0
2.2 8.6 13.8 5.4 10.2 4.9 6.8 14.0 2.0 10.5
2.1 5.7 5.1 16.8 6.0 11.1 1.3 11.2 7.7 4.9
2.3 10.0 16.7 12.0 12.4 7.8 5.2 13.6 2.6 22.4
3.6 7.1 8.8 25.6 3.2 18.3 5.1 2.0 3.0 12.0
22.2 10.8 5.5 2.0 24.3 9.9 3.6 5.6 4.4 7.9
5.1 24.5 6.4 7.5 4.7 20.5 5.5 15.7 2.6 5.7
5.5 6.0 16.0 2.4 9.5 3.7 17.0 3.8 4.1 2.3
5.3 7.8 8.1 4.3 13.3 6.8 1.3 7.0 4.9 1.8
7.1 28.0 10.2 13.8 17.9 10.1 5.5 4.6 3.2 21.6
(3)通过计算可以发现,平均数由原来的8.79 t变为9.483 t,中位数没有变化,还是6.8 t.这是因为样本平均数与每一个样本数据有关,样本中的任何一个数据的改变都会引起平均数的改变;但中位数只利用了样本数据中间位置的一个或两个值,并未利用其他数据,所以不是任何一个样本数据的改变都会引起中位数的改变.
课堂探究
总结:
与中位数比较,平均数反映出样本数据中的更多信息,对样本中的极端值更加敏感.
(2)假设有2 000户,该小区月均用水总量为.
课堂探究
思考:平均数和中位数都描述了数据的集中趁势,它们的大小关系和数据分布的形态有关.在下图的三种分布形态中,平均数和中位数的大小存在什么关系
(1)平均数和中位数应该大体上差不多;(对称)
(2)平均数大于中位数;(右边“拖尾”)
(3)平均数小于中位数.(左边“拖尾”)
总结:
在直方图中,平均数总在“长尾巴”那边.
课堂
任务三 探究众数
课堂探究
探究:某学校要定制高一年级的校服,学生根据厂家提供的参考身高选择校服规格.据统计,高一年级女生需要不同规格校服的频数如下表所示.
(1)如果用一个量来代表该校高一年级女生所需校服的规格,那么在中位数、平均数和众数中,哪个量比较合适
(2)试讨论用上表中的数据估计全国高一年级女生校服规格的合理性.
校服规格 155 160 165 170 175 合计
频数 39 64 167 90 26 386
解:(1)为了更直观地观察数据的特征,我们用条形图表示表中的数据(如右图).可以发现,选择校服规格为“165”的女生的频数最高,所以用众数165作为该校高一年级女生校服的规格比较合适.
课堂探究
总结:
一般地,对数值型数据(如用水量、身高、收入、产量等)集中趋势的描述,可以用平均数、中位数;而对分类型数据(如校服规格、性别、产品质量等级等)集中趋势的描述,可以用众数.
(2)由于全国各地的高一年级女生的身高存在一定的差异,所以用一个学校的数据估计全国高一年级女生的校服规格不合理.
课堂
任务四 探究利用频率分布直方图估计数据的集中趋势
课堂探究
说一说:我们在报纸、网络上获得的往往是已经整理好的统计表或统计图.
是否可以估计样本的平均数、中位数和众数
可以估算,在频率分布直方图中,我们无法知道每个组内的数据是如何分布的.此时,通常假设它们在组内均匀分布,这样就可以获得样本的平均数、中位数和众数的近似估计,进而估计总体的平均数、中位数和众数.
思考
你能以下图中频率分布直方图提供的信息为例,给出估计方法吗?(小组交流)
众数:最高矩形的中点横坐标.
课堂探究
中位数:左边和右边的直方图的面积应该相等.
样本平均数:可以用每个小矩形底边中点的横坐标与小矩形的面积的乘积之和 近似代替.
解:平均数的近似值
为
这个结果与根据原始数据计算的样本平均数8.79相差不大.
由于,因此中位数落在区间内;
设中位数为,由,
得到因此,中位数约为6.71,这个结果与根据原始数据求得的中位数6.8很接近.
平均数为8.96大于中位数6.71,符合右边“拖尾”的特点,即平均数大于中位数.
在频率分布直方图中,月均用水量在区间[4.2,7.2)内的居民最多,可以将这个区间的中点5.7作为众数的估计值.
课堂探究
课堂探究
各抒己见 假设你到人力市场去找工作,有一个企业老板告诉你,“我们企业员工的年平均收入是20万元”,你该如何理解这句话
以下方甲、乙两家10人公司为例,观察两组数据,你发现了什么?
员工编号 1 2 3 4 5 6 7 8 9 10
年收入/万元 20 21 19 23 21 20 16 20 22 18
甲公司员工年平均收入情况表
乙公司员工年平均收入情况表
员工编号 1 2 3 4 5 6 7 8 9 10
年收入/万元 5 10 120 7 8 15 10 15 5 5
课堂探究
归纳总结
对平均数、中位数、众数做比较
课堂
课堂探究
三、应用举例
【例1】根据如图所示的频率分布直方图求出样本数据的众数、中位数和平均数.
解:在中的数据最多,取这个区间的中点值作为众数的近似 值,得众数约为125.5.
中位数左边和右边的直方图的面积相等,设中位数为x,
则由图可知x,则
解得,即中位数约为125.75.
使用组中值求平均数,
即平均数约为125.8.
课堂
课堂探究
三、应用举例
【例2】据了解,某公司的33名职工月工资(单位:元)如下:
职务 董事长 副董事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 11 000 10 000 9 000 8 000 6 500 5 500 4 000
(1) 求该公司职工月工资的平均数、中位数、众数(精确到1);
(2) 假设副董事长的工资从10 000元提升到20 000元,董事长的工资从11 000元提升到30 000元,那么新的平均数、中位数、众数又是多少(精确到整数)
(3) 你认为哪个统计量更能反映这个公司员工的工资水平 结合此问题谈一谈你的看法.
解:(1)平均数是(元).
中位数是4 000元,众数是4 000元.
(2) 平均数是(元).
中位数是4 000元,众数是4 000元.
(3) 在这个问题中,中位数和众数均能反映该公司员工的工资水平,因为公司中少数人的工资额与大多数人的工资额差别较大,这样导致平均数偏差较大,所以平均数不能准确反映这个公司员工的工资水平.
课堂探究
归纳新知
众数、中位数、平均数的应用特点
(1)平均数与每一个数据都有关,可以反映更多的总体信息,但受极端值的影响大.
(2)中位数是样本数据所占频率的等分线,不受极端值的影响,当一组数据中存在极端值时,可用中位数描述这组数据的集中趋势.
(3)众数只能体现数据的最大集中点,无法客观反映总体特征.
课堂探究
评价反馈
1.一组样本数据为:19,23,12,14,14,17,10,12,18,14,27,则这组数据的众数和中位数分别为( )
14,14 B. 12,14
C. 14, D. 12,
解析:把这组数据按从小到大排列为10,12,12,14,14,14,17,18,19,23,27,则可知其众数为14,中位数为14.
A
评价反馈
解析:众数是指出现次数最多的数据,所以,将这组数据按从小到大的顺序排列:,6,6,8,12,中位数是指处于中间位置的数,即为6,平均数为
.故选.
2.(多选)已知一组数据为,6,8,,12,且这组数据的众数为6,那么下列说法正确的是( )
数据的中位数是6 B. 数据的平均数是6
C. D.
评价反馈
解析:最高分为94,若8为最低分,则平均分为,故最低分为88.设看不见的个位数为,则去掉最高分94和最低分88,平均分为,解得,故该数为89.
89
3.在一次比赛上,9位评委给参赛选手甲打出的分数为88,89,8●,93,92,91,92,91,94.去掉一个最高分和一个最低分后,算得平均分为91,参赛选手复查时,发现有一个数的个位数字无法看清.若成绩计算无误,则该数为 .
评价反馈
4.(多选)甲、乙两名射击运动员在某次测试中各射击20次,两人测试成绩的条形图如图所示,则下列说法正确的是( )
A.甲运动员测试成绩的中位数等于乙运动员测试成绩的中位数
B.甲运动员测试成绩的众数大于乙运动员测试成绩的众数
C.甲运动员测试成绩的平均数大于乙运动员测试成绩的平均数
D.甲运动员测试成绩的第90百分位数等于乙运动员测试成绩的第90百分位数
AD
解析:
甲运动员测试成绩:3次7环,8次8环,5次9环,4次10环.所以中位数为8,众数为8,平均数为=8.5,第90百分位数为10.
乙运动员测试成绩:4次7环,7次8环,4次9环,5次10环.所以中位数为8,众数为8,平均数为=8.5,第90百分位数为10.故选AD.
评价反馈
解析:设丢失的数据为x,则这七个数据的平均数为,众数是4,因为这组数据的平均数与众数的和是中位数的2倍,若x≤4,则中位数为4,此时+4=2×4,解得x=-9;若4<x<7,则中位数为x,此时+4=2x,解得x=5;若x≥7,则中位数为7,此时+4=2×7,解得x=33.综上可知,丢失数据的所有可能的取值为-9,5,33,其构成的集合为{-9,5,33}.
评价反馈
5.(2024·绍兴月考)已知一组数据丢失了其中一个,剩下的六个数据分别是4,4,7,4,8,10,若这组数据的平均数与众数的和是中位数的2倍,则丢失数据的所有可能值组成的集合为 .
{-9,5,33}
评价反馈
6.某校高一年级举行了一次数学竞赛,为了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为n),按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,已知得分在[50,60),[90,100]内的频数分别为8,2.
(1)求样本容量n 和频率分布直方图中的x,y 的值;
(2)估计本次竞赛学生成绩的众数、中位数、平均数.
评价反馈
解:(1)由题意可知,样本容量n==50,
y==0.004,
x=0.1-0.016-0.040-0.010-0.004=0.030.
(2)由题中频率分布直方图可知,本次竞赛学生成绩的众数约为75.
设中位数为m,
∵(0.016+0.030)×10<0.5<(0.016+0.030+0.040)×10,则m∈[70,80),
∴(0.016+0.030)×10+(m-70)×0.040=0.5,
解得m=71,即本次竞赛学生成绩的中位数约为71.
本次竞赛学生成绩的平均数约为55×0.16+65×0.3+75×0.4+85×0.1+95×0.04=70.6.
课堂小结
通过本节课学习,你收获了哪些新知识与技能?通过什么方法学到的?体会到了什么数学思想?
1.已学习:众数、中位数、平均数的计算及总体集中趋势的估计.
2.须贯通:众数、中位数、平均数是真实数据的估计值,描述了真实数据的集 中趋势,在频率分布直方图中求这些数字特征时应用了数形结合的思想.
3.应注意:(1)一组数据的众数可能有一个、多个或不存在;
(2)求中位数时,应先将数据从小到大或从大到小排列.
布置作业
认真整理本节所讲知识,梳理知识脉络,完成学案的核心素养专练;
必做题:课本209页练习3、课本217页习题第9题.
选做题:课本225页复习参考题第11题
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
