第六章 6.4.3余弦定理、正弦定理第3课时--人教A版高中数学必修第二册教学课件(共26张PPT)
文档属性
| 名称 | 第六章 6.4.3余弦定理、正弦定理第3课时--人教A版高中数学必修第二册教学课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:47:20 | ||
图片预览






文档简介
(共26张PPT)
6.4.3余弦定理 、正弦
定理 第3课时 余弦定理 、正弦定理应用举例
第六章 平面向量及其应用
数学
学习目标
①掌握应用正弦定理、余弦定理解决实际问题的基本分析方法和步骤,达到直观想象和逻辑推理核心素养水平一的要求.
②能够运用正弦定理和余弦定理解三角形的知识,解决不可到达点的距离测量问题(包括测量长度、高度和角度等),达到数学运算核心素养水平一的要求.
③通过实际问题情境,提升学生的数学抽象、数学建模等数学素养,使其能够运用数学语言准确描述问题,并运用所学的数学知识进行分析和解决.
学习重难点
重点:
由实际问题中抽象出一个或几个三角形,然后逐个解决,得到实际问题的解.
难点:
根据题意建立数学模型,画出示意图.
阅读课本48-51页,思考并完成以下问题:
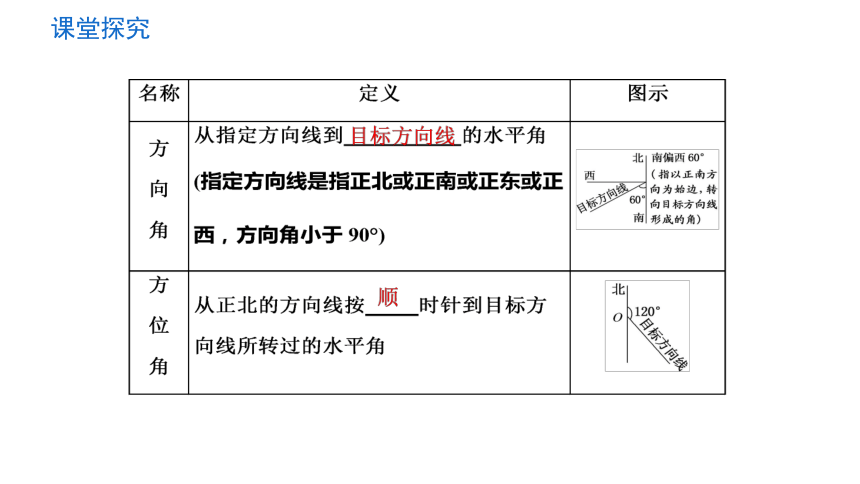
1、方向角和方位角各是什么样的角?
2、怎样测量物体的高度?
3、怎样测量物体所在的角度?
自主预习
课堂导入
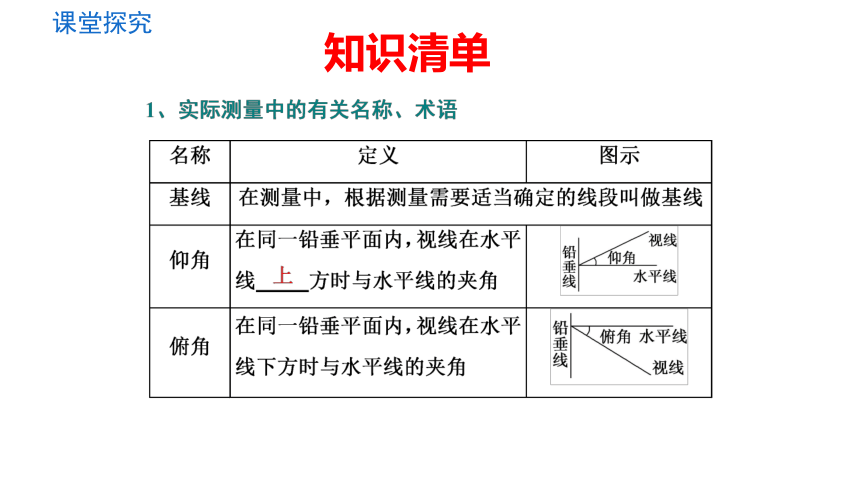
知识清单
课堂探究
课堂探究
题型分析
课堂探究
课堂探究
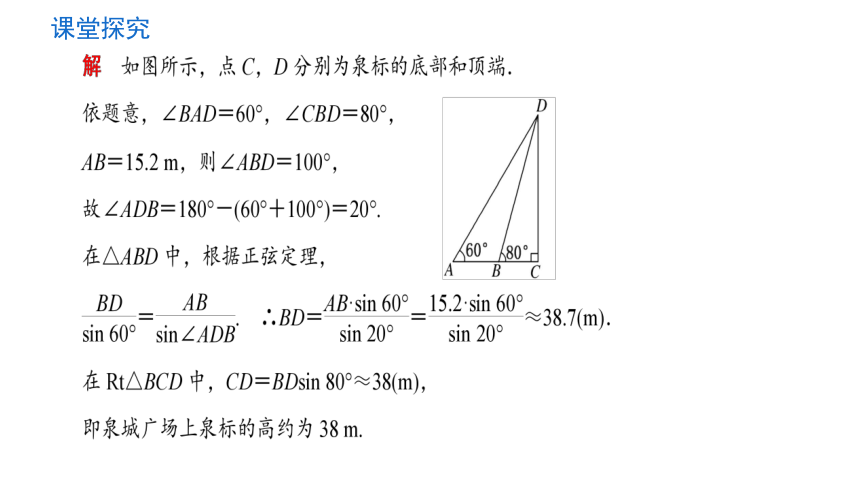
解题技巧(测量高度技巧)
课堂探究
【跟踪训练1】
课堂探究
课堂探究
课堂探究
课堂探究
解题技巧(测量角度技巧)
课堂探究
【跟踪训练2】
课堂探究
课堂探究
例3 (1)如图所示,A,B两点在一条河的两岸,测量者在A的同侧,且点B不可到达,要测出A,B的距离,应在A所在的岸边选定一点C,可以测出A,C的距离,再借助仪器,测出∠BCA,∠BAC,在△ABC中,运用正弦定理就可以求出AB.若测出AC=60 m,∠BAC=75°,∠BCA=45°,则A,B两点间的距离为 m.
课堂探究
(1)答案 20
解析 由题意知∠ABC=180°-75°-45°=60°,
所以由正弦定理,得
AB==20(m),
即A,B两点间的距离为20 m.
20
课堂探究
课堂探究
解题技巧(测量距离技巧)
课堂探究
课堂探究
【跟踪训练3】
课堂探究
课堂探究
课堂小结
总结归纳
1.解决应用题的思想方法是什么
把实际问题转化为数学问题,即数学建模思想.
2.求解三角形应用题的一般步骤:
(1)审题:分析题意,弄清已知和所求,根据题意,画出示意图;
(2)建模:将实际问题转化为解三角形的数学问题;
(3)求模:正确运用正、余弦定理求解;
(4)还原:还原实际问题的解.
布置作业
必做题:教材51页练习,52—54页习题6.4中剩余题.
选做题:素质专项训练
谢谢大家
6.4.3余弦定理 、正弦
定理 第3课时 余弦定理 、正弦定理应用举例
第六章 平面向量及其应用
数学
学习目标
①掌握应用正弦定理、余弦定理解决实际问题的基本分析方法和步骤,达到直观想象和逻辑推理核心素养水平一的要求.
②能够运用正弦定理和余弦定理解三角形的知识,解决不可到达点的距离测量问题(包括测量长度、高度和角度等),达到数学运算核心素养水平一的要求.
③通过实际问题情境,提升学生的数学抽象、数学建模等数学素养,使其能够运用数学语言准确描述问题,并运用所学的数学知识进行分析和解决.
学习重难点
重点:
由实际问题中抽象出一个或几个三角形,然后逐个解决,得到实际问题的解.
难点:
根据题意建立数学模型,画出示意图.
阅读课本48-51页,思考并完成以下问题:
1、方向角和方位角各是什么样的角?
2、怎样测量物体的高度?
3、怎样测量物体所在的角度?
自主预习
课堂导入
知识清单
课堂探究
课堂探究
题型分析
课堂探究
课堂探究
解题技巧(测量高度技巧)
课堂探究
【跟踪训练1】
课堂探究
课堂探究
课堂探究
课堂探究
解题技巧(测量角度技巧)
课堂探究
【跟踪训练2】
课堂探究
课堂探究
例3 (1)如图所示,A,B两点在一条河的两岸,测量者在A的同侧,且点B不可到达,要测出A,B的距离,应在A所在的岸边选定一点C,可以测出A,C的距离,再借助仪器,测出∠BCA,∠BAC,在△ABC中,运用正弦定理就可以求出AB.若测出AC=60 m,∠BAC=75°,∠BCA=45°,则A,B两点间的距离为 m.
课堂探究
(1)答案 20
解析 由题意知∠ABC=180°-75°-45°=60°,
所以由正弦定理,得
AB==20(m),
即A,B两点间的距离为20 m.
20
课堂探究
课堂探究
解题技巧(测量距离技巧)
课堂探究
课堂探究
【跟踪训练3】
课堂探究
课堂探究
课堂小结
总结归纳
1.解决应用题的思想方法是什么
把实际问题转化为数学问题,即数学建模思想.
2.求解三角形应用题的一般步骤:
(1)审题:分析题意,弄清已知和所求,根据题意,画出示意图;
(2)建模:将实际问题转化为解三角形的数学问题;
(3)求模:正确运用正、余弦定理求解;
(4)还原:还原实际问题的解.
布置作业
必做题:教材51页练习,52—54页习题6.4中剩余题.
选做题:素质专项训练
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
