第六章 本章小结--人教A版高中数学必修第二册教学课件(共22张PPT)
文档属性
| 名称 | 第六章 本章小结--人教A版高中数学必修第二册教学课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-01 10:47:25 | ||
图片预览





文档简介
(共22张PPT)
章末总结
第六章 平面向量及其应用
数学
学习目标
①理解平面向量的概念,掌握平面向量的运算.
②理解并掌握平面向量基本定理及坐标表示.
③掌握平面向量的应用,掌握解三角形.
学习重难点
重点:
向量的概念,向量的加减法,向量的数乘运算,向量的数量积,平面向量基本定理,向量运算的坐标表示,余弦定理,正弦定理.
难点:
用向量方法解决数学和物理学科中问题,需要综合运用向量知识、其他数学知识或物理知识,探寻解决问题的途径.
内容 考点 关注点
平面 向量 向量的线性运算 运算法则
向量的数量积、模、夹角 夹角范围
向量的坐标运算 公式运用
向量的平行与垂直问题 向量的方向与数量积正负的关系
利用正弦定理、余弦定理解三角形 选择合适的定理及三角形
课堂导入
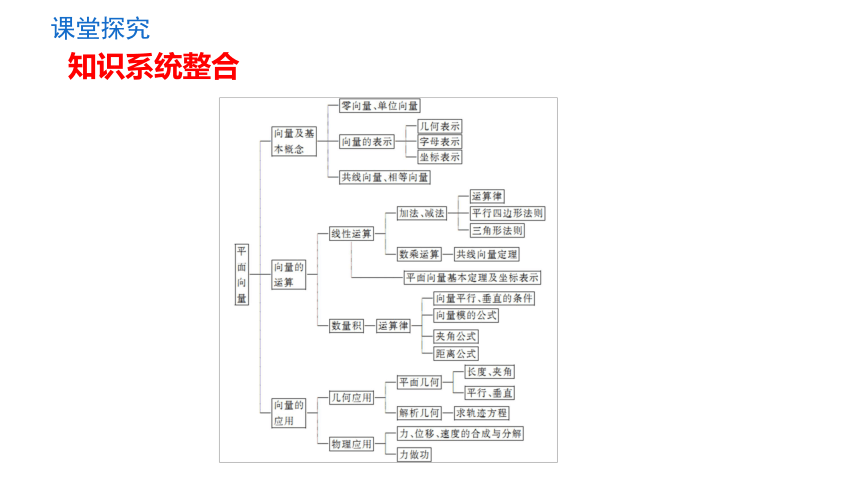
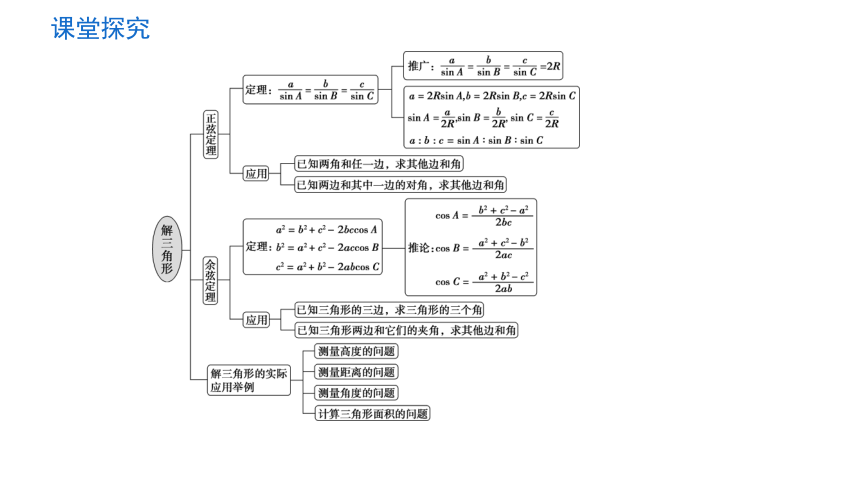
知识系统整合
课堂探究
课堂探究
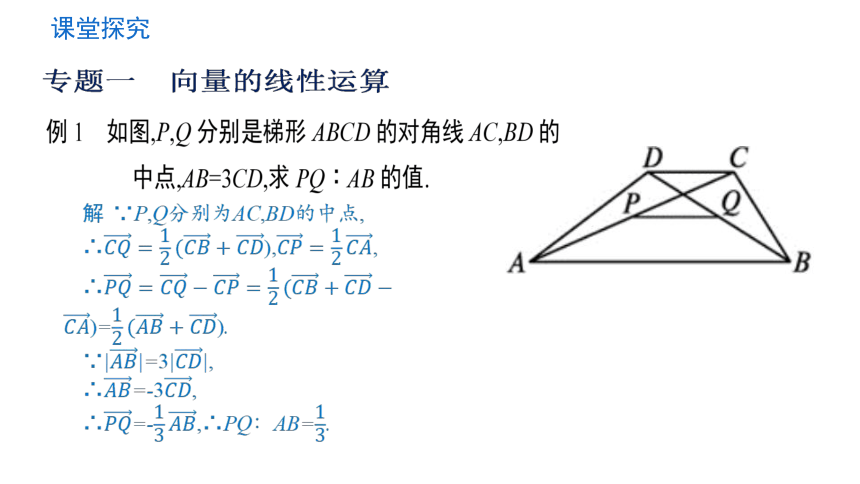
课堂探究
解 ∵P,Q分别为AC,BD的中点,
∴),,
∴)=).
∵||=3||,
∴=-3,
∴=-,∴PQ∶AB=.
知识点二 平面向量数量积的运算
课堂探究
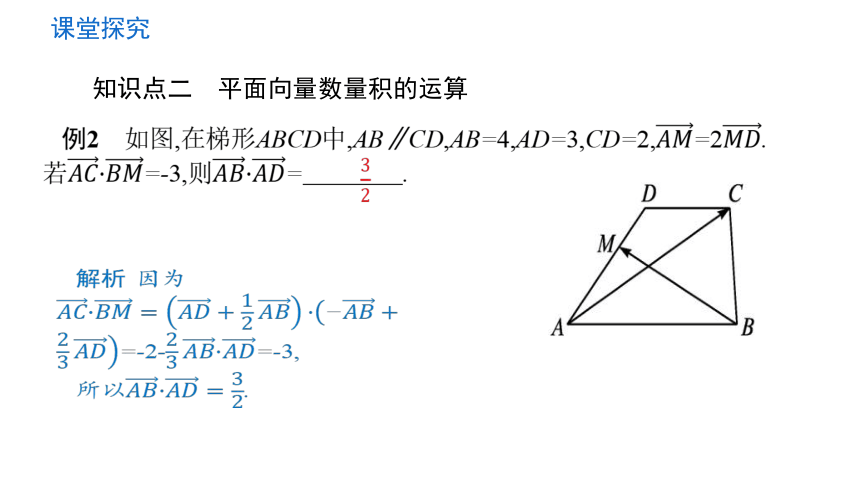
例2 如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,=2.若=-3,则= .
解析 因为=-2-=-3,
所以.
知识点三 平面向量的坐标运算
例3 已知向量a=(2,0),b=(1,).
(1)若(λa-b)⊥b,求λ的值;
(2)若m=λa+μb,且|m|=2,m与b的夹角为,求λ,μ的值.
解 (1)因为a=(2,0),b=(1,),
所以λa-b=(2λ,0)-(1,)=(2λ-1,-).
又(λa-b)⊥b,
所以(λa-b)·b=2λ-1-3=0,
所以λ=2.
课堂探究
(2)因为a=(2,0),b=(1,),
所以m=λa+μb=λ(2,0)+μ(1,)=(2λ+μ,μ).
因为|m|=2,m与b的夹角为,
所以
即
解得
课堂探究
知识点四 平面向量的平行与垂直问题
1.证明平面向量共线问题常用的方法
(1)向量a,b(a≠0)共线 存在唯一实数λ,使b=λa.
(2)向量a=(x1,y1),b=(x2,y2)共线 x1y2-x2y1=0.
(3)向量a与b共线 |a·b|=|a||b|.
(4)向量a与b共线 存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.
2.证明平面向量垂直问题的常用方法
a⊥b a·b=0 x1x2+y1y2=0,其中a=(x1,y1),b=(x2,y2).
课堂探究
例4 (1)已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ=( )
A.-4 B.-3 C.-2 D.-1
解析 因为m+n=(2λ+3,3),m-n=(-1,-1),
且(m+n)⊥(m-n),
所以(m+n)·(m-n)=-2λ-3-3=0,
解得λ=-3.故选B.
B
(2)设A,B,C,D为平面内的四点,且A(1,3),B(2,-2),C(4,1).
①若,求点D的坐标;
②设向量a=,b=,若ka-b与a+3b平行,求实数k的值.
课堂探究
(2)解 ①设点D的坐标为(x,y),因为,
所以(2,-2)-(1,3)=(x,y)-(4,1),
所以解得
所以点D的坐标为(5,-4).
②因为a==(2,-2)-(1,3)=(1,-5),b==(4,1)-(2,-2)=(2,3),
所以ka-b=k(1,-5)-(2,3)=(k-2,-5k-3),a+3b=(1,-5)+3(2,3)=(7,4).
因为ka-b与a+3b平行,所以7(-5k-3)-4(k-2)=0,
解得k=-.
知识点五 平面向量的模、夹角问题
1.解决向量模的问题常用的策略
(1)应用公式:|a|=,其中a=(x,y).
(2)应用三角形或平行四边形法则.
(3)应用向量不等式||a|-|b||≤|a±b|≤|a|+|b|.
(4)研究模的平方|a±b|2=(a±b)2.
2.求向量的夹角
设非零向量a=(x1,y1),b=(x2,y2),两向量的夹角θ(0≤θ≤π)的余弦cos θ=.
课堂探究
例5 已知向量e1,e2,且|e1|=|e2|=1,e1与e2的夹角为,m=λe1+e2,n=3e1-2e2.
(1)求证:(2e1-e2)⊥e2;
(2)若|m|=|n|,求λ的值;
(3)若m⊥n,求λ的值;
(4)若m与n的夹角为,求λ的值.
课堂探究
(1)证明 因为|e1|=|e2|=1,e1与e2的夹角为,
所以(2e1-e2)·e2=2e1·e2-=2|e1||e2|cos-|e2|2=2×1×1×-12=0,
所以(2e1-e2)⊥e2.
(2)解 由|m|=|n|,得(λe1+e2)2=(3e1-2e2)2,即(λ2-9)+(2λ+12)e1·e2-3=0.
因为|e1|=|e2|=1,e1与e2的夹角为,
所以=1,e1·e2=1×1×cos,
所以(λ2-9)×1+(2λ+12)×-3×1=0,
即λ2+λ-6=0,解得λ=2或λ=-3.
课堂探究
课堂探究
(3)解 由m⊥n知m·n=0,
即(λe1+e2)·(3e1-2e2)=3λ+(3-2λ)e1·e2-2=3λ+(3-2λ)×-2=0,
解得λ=.
(4)解 |n|=,|m|2=(λe1+e2)2=λ2+2λe1·e2+=λ2+λ+1,
所以|m|=.
m·n=(λe1+e2)·(3e1-2e2)=3λ+(3-2λ)×-2=2λ-,
所以2λ-,
化简,得3λ2-5λ-2=0,
解得λ=2或λ=-.
当λ=-时,m·n=2λ-<0,m与n的夹角为钝角,不符合题意,故λ=2.
课堂探究
知识点六 利用正、余弦定理解三角形
例6 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acos B.
(1)证明:A=2B;
(2)若△ABC的面积S=,求角A的大小.
(1)证明 由已知及正弦定理,得
sin B+sin C=2sin Acos B,
故2sin Acos B=sin B+sin(A+B)=sin B+sin Acos B+cos Asin B,
于是sin B=sin Acos B-cos Asin B=sin(A-B).
又A,B∈(0,π),故-π所以B=π-(A-B)或B=A-B,
因此A=π(舍去)或A=2B,
所以A=2B.
课堂探究
(2)解 由S=,得absin C=,即bsin C=,
根据正弦定理,得sin Bsin C=sin A=sin 2B=sin Bcos B,
因为sin B>0,所以sin C=cos B,
又B,C∈(0,π),B+C∈(0,π),
所以C=±B.
又A=2B,所以当B+C=时,A=,
当C-B=时,A=.
综上,A=或A=.
课堂小结
总结归纳
我们今天都讲了哪些知识?
布置作业
必做题:教材第59—62页复习参考题6.
选做题:素质专项训练
谢谢大家
章末总结
第六章 平面向量及其应用
数学
学习目标
①理解平面向量的概念,掌握平面向量的运算.
②理解并掌握平面向量基本定理及坐标表示.
③掌握平面向量的应用,掌握解三角形.
学习重难点
重点:
向量的概念,向量的加减法,向量的数乘运算,向量的数量积,平面向量基本定理,向量运算的坐标表示,余弦定理,正弦定理.
难点:
用向量方法解决数学和物理学科中问题,需要综合运用向量知识、其他数学知识或物理知识,探寻解决问题的途径.
内容 考点 关注点
平面 向量 向量的线性运算 运算法则
向量的数量积、模、夹角 夹角范围
向量的坐标运算 公式运用
向量的平行与垂直问题 向量的方向与数量积正负的关系
利用正弦定理、余弦定理解三角形 选择合适的定理及三角形
课堂导入
知识系统整合
课堂探究
课堂探究
课堂探究
解 ∵P,Q分别为AC,BD的中点,
∴),,
∴)=).
∵||=3||,
∴=-3,
∴=-,∴PQ∶AB=.
知识点二 平面向量数量积的运算
课堂探究
例2 如图,在梯形ABCD中,AB∥CD,AB=4,AD=3,CD=2,=2.若=-3,则= .
解析 因为=-2-=-3,
所以.
知识点三 平面向量的坐标运算
例3 已知向量a=(2,0),b=(1,).
(1)若(λa-b)⊥b,求λ的值;
(2)若m=λa+μb,且|m|=2,m与b的夹角为,求λ,μ的值.
解 (1)因为a=(2,0),b=(1,),
所以λa-b=(2λ,0)-(1,)=(2λ-1,-).
又(λa-b)⊥b,
所以(λa-b)·b=2λ-1-3=0,
所以λ=2.
课堂探究
(2)因为a=(2,0),b=(1,),
所以m=λa+μb=λ(2,0)+μ(1,)=(2λ+μ,μ).
因为|m|=2,m与b的夹角为,
所以
即
解得
课堂探究
知识点四 平面向量的平行与垂直问题
1.证明平面向量共线问题常用的方法
(1)向量a,b(a≠0)共线 存在唯一实数λ,使b=λa.
(2)向量a=(x1,y1),b=(x2,y2)共线 x1y2-x2y1=0.
(3)向量a与b共线 |a·b|=|a||b|.
(4)向量a与b共线 存在不全为零的实数λ1,λ2,使λ1a+λ2b=0.
2.证明平面向量垂直问题的常用方法
a⊥b a·b=0 x1x2+y1y2=0,其中a=(x1,y1),b=(x2,y2).
课堂探究
例4 (1)已知向量m=(λ+1,1),n=(λ+2,2),若(m+n)⊥(m-n),则λ=( )
A.-4 B.-3 C.-2 D.-1
解析 因为m+n=(2λ+3,3),m-n=(-1,-1),
且(m+n)⊥(m-n),
所以(m+n)·(m-n)=-2λ-3-3=0,
解得λ=-3.故选B.
B
(2)设A,B,C,D为平面内的四点,且A(1,3),B(2,-2),C(4,1).
①若,求点D的坐标;
②设向量a=,b=,若ka-b与a+3b平行,求实数k的值.
课堂探究
(2)解 ①设点D的坐标为(x,y),因为,
所以(2,-2)-(1,3)=(x,y)-(4,1),
所以解得
所以点D的坐标为(5,-4).
②因为a==(2,-2)-(1,3)=(1,-5),b==(4,1)-(2,-2)=(2,3),
所以ka-b=k(1,-5)-(2,3)=(k-2,-5k-3),a+3b=(1,-5)+3(2,3)=(7,4).
因为ka-b与a+3b平行,所以7(-5k-3)-4(k-2)=0,
解得k=-.
知识点五 平面向量的模、夹角问题
1.解决向量模的问题常用的策略
(1)应用公式:|a|=,其中a=(x,y).
(2)应用三角形或平行四边形法则.
(3)应用向量不等式||a|-|b||≤|a±b|≤|a|+|b|.
(4)研究模的平方|a±b|2=(a±b)2.
2.求向量的夹角
设非零向量a=(x1,y1),b=(x2,y2),两向量的夹角θ(0≤θ≤π)的余弦cos θ=.
课堂探究
例5 已知向量e1,e2,且|e1|=|e2|=1,e1与e2的夹角为,m=λe1+e2,n=3e1-2e2.
(1)求证:(2e1-e2)⊥e2;
(2)若|m|=|n|,求λ的值;
(3)若m⊥n,求λ的值;
(4)若m与n的夹角为,求λ的值.
课堂探究
(1)证明 因为|e1|=|e2|=1,e1与e2的夹角为,
所以(2e1-e2)·e2=2e1·e2-=2|e1||e2|cos-|e2|2=2×1×1×-12=0,
所以(2e1-e2)⊥e2.
(2)解 由|m|=|n|,得(λe1+e2)2=(3e1-2e2)2,即(λ2-9)+(2λ+12)e1·e2-3=0.
因为|e1|=|e2|=1,e1与e2的夹角为,
所以=1,e1·e2=1×1×cos,
所以(λ2-9)×1+(2λ+12)×-3×1=0,
即λ2+λ-6=0,解得λ=2或λ=-3.
课堂探究
课堂探究
(3)解 由m⊥n知m·n=0,
即(λe1+e2)·(3e1-2e2)=3λ+(3-2λ)e1·e2-2=3λ+(3-2λ)×-2=0,
解得λ=.
(4)解 |n|=,|m|2=(λe1+e2)2=λ2+2λe1·e2+=λ2+λ+1,
所以|m|=.
m·n=(λe1+e2)·(3e1-2e2)=3λ+(3-2λ)×-2=2λ-,
所以2λ-,
化简,得3λ2-5λ-2=0,
解得λ=2或λ=-.
当λ=-时,m·n=2λ-<0,m与n的夹角为钝角,不符合题意,故λ=2.
课堂探究
知识点六 利用正、余弦定理解三角形
例6 在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acos B.
(1)证明:A=2B;
(2)若△ABC的面积S=,求角A的大小.
(1)证明 由已知及正弦定理,得
sin B+sin C=2sin Acos B,
故2sin Acos B=sin B+sin(A+B)=sin B+sin Acos B+cos Asin B,
于是sin B=sin Acos B-cos Asin B=sin(A-B).
又A,B∈(0,π),故-π
因此A=π(舍去)或A=2B,
所以A=2B.
课堂探究
(2)解 由S=,得absin C=,即bsin C=,
根据正弦定理,得sin Bsin C=sin A=sin 2B=sin Bcos B,
因为sin B>0,所以sin C=cos B,
又B,C∈(0,π),B+C∈(0,π),
所以C=±B.
又A=2B,所以当B+C=时,A=,
当C-B=时,A=.
综上,A=或A=.
课堂小结
总结归纳
我们今天都讲了哪些知识?
布置作业
必做题:教材第59—62页复习参考题6.
选做题:素质专项训练
谢谢大家
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
